高中数学北师大版必修3课件:习题课1 统计 :34张PPT
文档属性
| 名称 | 高中数学北师大版必修3课件:习题课1 统计 :34张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 900.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 12:24:09 | ||
图片预览









文档简介
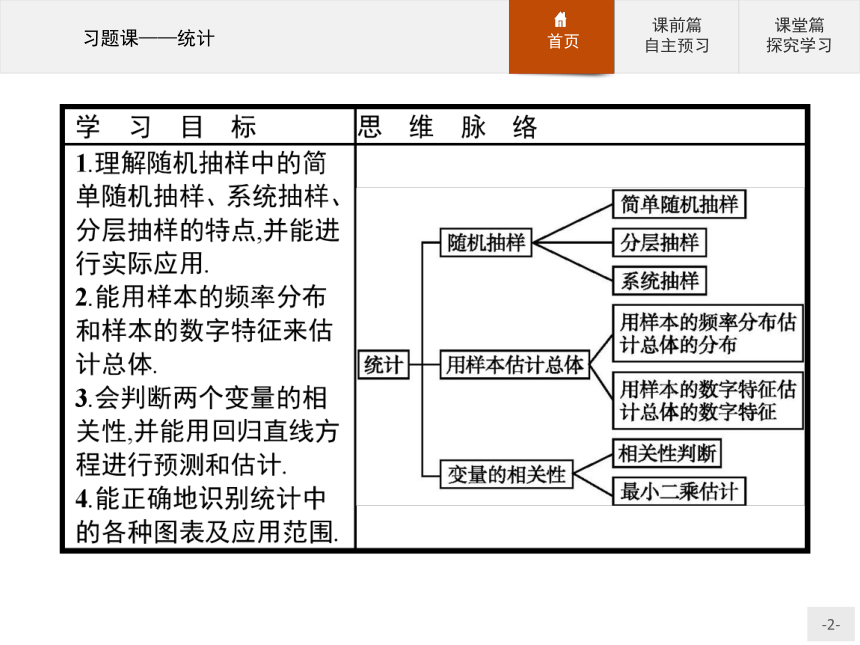
课件34张PPT。习题课——统计一、三种抽样方法
1.当总体容量较小,样本容量较小时,采用抽签法.
2.当总体容量较大,样本容量较小时,采用随机数法.
3.当总体容量较大,样本容量较大时,采用系统抽样法.
4.当总体由差异明显的几部分组成时,采用分层抽样法.
二、统计图表的特点与选择
1.若只需大致判断一些数据的分布规律,了解数据各元素所占比例的大小情况可以用扇形统计图;
2.若需要根据图表了解各个数据所占的频率可以使用条形统计图;
3.若要了解数据的增减情况可以采用折线图;
4.若要了解数据的全部信息可以用茎叶图.三、数据的数字特征
1.在样本数据中,出现次数最多的那个数据叫做众数.
2.将数据按大小排列,位于中间的数据(或中间两数的平均数)称为中位数.
3.平均数具有对数据进行“取齐”的作用,它代表了数据取值的平均水平,在频率分布直方图中,平均数是其平衡点.四、用样本估计总体
1.在频率分布直方图中,纵坐标的含义为 .
2.在频率分布直方图中,所有小长方形的面积和为1,每个小长方形的面积代表对应该组数据出现的频率.
3.频率分布折线图是把频率分布直方图中各个矩形上边的中点用线段连接起来而得到的,它不但可以表示出数量的多少,而且能清楚直观地表示数量增减的变化情况.
五、线性回归分析
1.变量与变量之间存在两种关系,一种确定性的关系为函数关系;另一种变量间确实存在关系,但带有随机性的为相关关系.
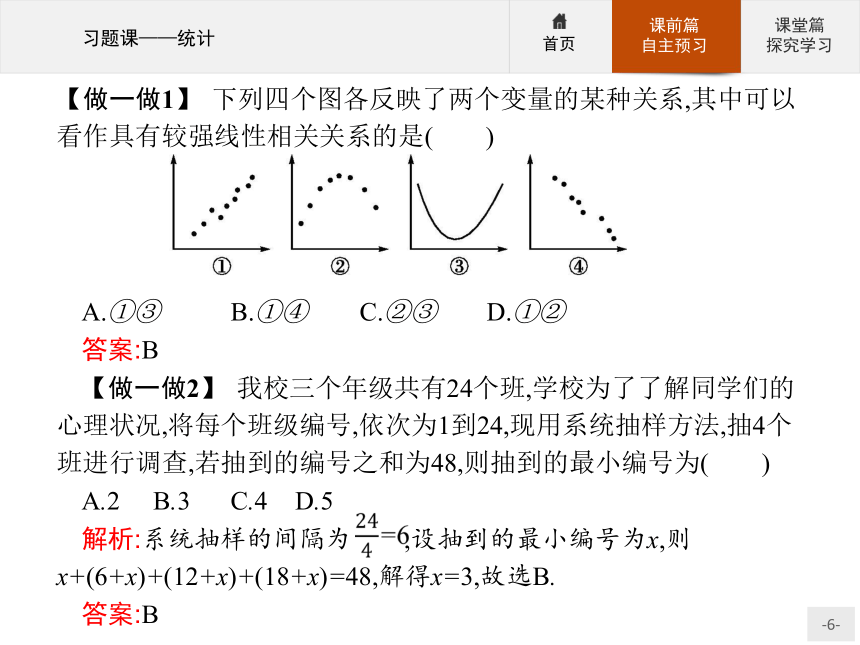
2.求线性回归方程的前提是两个变量具有线性相关关系,样本数据越多,变量间的相关程度越高,估计越精确.【做一做1】 下列四个图各反映了两个变量的某种关系,其中可以看作具有较强线性相关关系的是( )A.①③ B.①④ C.②③ D.①②
答案:B
【做一做2】 我校三个年级共有24个班,学校为了了解同学们的心理状况,将每个班级编号,依次为1到24,现用系统抽样方法,抽4个班进行调查,若抽到的编号之和为48,则抽到的最小编号为( )
A.2 B.3 C.4 D.5
解析:系统抽样的间隔为 ,设抽到的最小编号为x,则x+(6+x)+(12+x)+(18+x)=48,解得x=3,故选B.
答案:B 【做一做3】 已知某种产品的支出广告额x与利润额y(单位:万元)之间有如下对应数据:则回归直线必过( )
A.(5,36) B.(5,35) C.(5,30) D.(4,30)答案:A 【做一做4】 如图是一组样本数据的频率分布直方图,则依据图形中的数据,可以估计总体的平均数与中位数分别是( )
A.12.5,12.5
B.13,13
C.13.5,12.5
D.13.5,13
解析:根据频率分布直方图可以得到第一组的频率为0.2,第二组的频率为0.5,则第三组的频率为0.3,
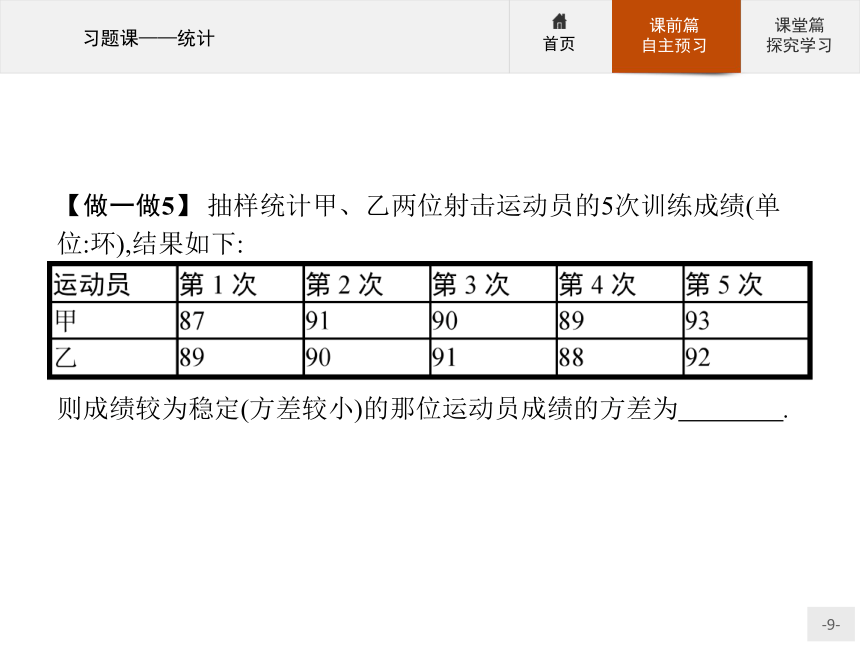
则平均数为7.5×0.2+12.5×0.5+17.5×0.3=13,答案:B 【做一做5】 抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:则成绩较为稳定(方差较小)的那位运动员成绩的方差为 .?答案:2 探究一探究二探究三思维辨析当堂检测抽样方法的应用【例1】 问题:①某小区有800户家庭,其中高收入家庭200户,中等收入家庭480户,低收入家庭120户,为了了解有关家用轿车购买力的某个指标,要从中抽取一个容量为100的样本;②从10名学生中抽取3人参加座谈会.方法:(1)简单随机抽样;(2)系统抽样;(3)分层抽样.则问题与方法配对正确的是( )
A.①(1),②(2) B.①(3),②(2)
C.①(2),②(3) D.①(3),②(1)
解析:问题①中的总体是由差异明显的几部分组成的,故可采用分层抽样方法;问题②中总体的个数较少,故可采用简单随机抽样.故匹配正确的是D.
答案:D探究一探究二探究三思维辨析当堂检测反思感悟1.想要合理地选用抽样方法,需要明确各种抽样方法的特点及应用范围.
2.当问题中需要剔除某些个体的时候,也要“随机”,而不是“随便”.探究一探究二探究三思维辨析当堂检测 变式训练1某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的 ,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.探究一探究二探究三思维辨析当堂检测解:(1)设登山组人数为x,游泳组中青年人、中年人、老年人各占比例分别为a,b,c.探究一探究二探究三思维辨析当堂检测统计的基本思想及应用
【例2】 有一容量为200的样本,数据的分组以及各组的频数如下:
-20~-15,7;-15~-10,11;-10~-5,15;-5~0,40;0~5,
49;5~10,41;10~15,20;15~20,17.
(1)列出样本的频率分布表;
(2)画出频率分布直方图和频率分布折线图;
(3)求样本数据不足0的频率.探究一探究二探究三思维辨析当堂检测解:(1)频率分布表如下: 探究一探究二探究三思维辨析当堂检测(2)如图是频率分布直方图和频率分布折线图:
?
(3)样本数据不足0的频率为:
0.035+0.055+0.075+0.2=0.365.探究一探究二探究三思维辨析当堂检测反思感悟统计思想的应用技巧
1.用样本的频率分布估计总体分布时,绘制茎叶图、频率分布直方图等图形是关键,借助数形结合法易得到总体的分布情况.
2.计算样本的数字特征,如平均数、标准差等,根据样本的数据特点,正确地选用公式,采用简便的算法,从而估计出总体的数字特征,并对总体作出相应的估计.探究一探究二探究三思维辨析当堂检测 变式训练2某市一体校拟选拔一名帆船运动员参加省大学生运动会,对帆船运动员甲、乙两人在相同的条件下进行了6次测试,测得他们速度的数据如下:
甲:27,38,30,37,35,31;
乙:33,29,38,34,28,36.
(1)将这两组数据用茎叶图表示.
(2)根据题中数据,请你在甲、乙两人中确定参加省大学生运动会的帆船运动员,并说明理由.探究一探究二探究三思维辨析当堂检测 解:(1)由题意可得:这两组数据的茎叶图为: 探究一探究二探究三思维辨析当堂检测 线性回归分析及应用【例3】 某地连续十年粮食需求量逐年上升,下表是部分统计数据:
(1)利用所给数据求年需求量与年份之间的回归方程
(2)利用(1)中所求出的直线方程预测该地2020年的粮食需求量.
分析因为所给数据比较大,所以可以对数据进行初步处理,减少计算量.然后代入公式求解回归系数,利用回归直线方程预测时,也要注意数据的处理.探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测反思感悟线性回归是处理变量之间的线性相关关系的一种数理统计方法,它为生产、生活提供了一种科学的测算依据,如果两个变量线性相关,那么一定可以找到一条直线拟合该关系,关键是如何找出这样一条最佳拟合直线,即如何求得线性回归方程,利用线性回归方程对两个变量间的线性关系进行估计,实际上就是将非确定性的相关关系问题转化为确定性的函数关系进行研究,我们常用的方法就是“最小二乘法”,它使得样本数据的点到它的距离的平方和最小.探究一探究二探究三思维辨析当堂检测(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a.
(2)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.探究一探究二探究三思维辨析当堂检测未弄清频率分布直方图中数字特征的意义而致误
【典例】某城市100户居民的月平均用电量(单位:千瓦时),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数.探究一探究二探究三思维辨析当堂检测错解:(1)由(0.002+0.009 5+0.011+0.012 5+x+0.005+0.002 5)×20=1得x=0.007 5,
所以直方图中x的值是0.007 5.
(2)由众数的定义知,月平均用电量的众数是220~240.因为(0.002+0.009 5+0.011)×20=0.45<0.5,所以月平均用电量的中位数在[220,240)内,即为
正解:(1)由(0.002+0.009 5+0.011+0.012 5+x+0.005+0.002 5)×20=1,得x=0.007 5,
所以直方图中x的值是0.007 5.
(2)月平均用电量的众数是
因为(0.002+0.009 5+0.011)×20=0.45<0.5,所以月平均用电量的中位数在[220,240)内,设中位数为a,由(0.002+0.009 5+0.011)×20+0.012 5×(a-220)=0.5得a=224,所以月平均用电量的中位数是224.探究一探究二探究三思维辨析当堂检测纠错心得1.本题出现错误的根源是对频率分布直方图中的数字特征的意义理解不清,要知道,在频率分布直方图中众数是最高的矩形的底边中点的横坐标,是一个数,而不是范围.
2.在频率分布直方图中,中位数左右两侧直方图的面积相等,小矩形的高度代表的是对应该组数据 的值,只有明确了这些数据特征,才能做到有的放矢.探究一探究二探究三思维辨析当堂检测变式训练一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中用分层抽样方法抽出80人做进一步调查,则在[1 500,2 000)(元)月收入段应抽出 人.?探究一探究二探究三思维辨析当堂检测解:析:由频率分布直方图知,收入在1 500~2 000元之间的频率为0.000 4×500=0.2,所以在[1 500,2 000)(元)月收入段应抽出80×0.2=16(人).
答案:16探究一探究二探究三思维辨析当堂检测1.某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名,现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
A.6 B.8 C.10 D.12
解析:设从高二年级抽取的学生数为n,
答案:B探究一探究二探究三思维辨析当堂检测2.某产品的广告费用x与销售额y的统计数据如下表:根据上表可得回归方程y=bx+a中的b=10.6,据此模型预报广告费用为10万元时销售额为( )
A.112.1万元 B.113.1万元
C.113.9万元 D.111.9万元答案:D 探究一探究二探究三思维辨析当堂检测3.如图是某中学甲、乙两名学生2017年上半年篮球比赛每场比赛得分的茎叶图,则甲、乙两名学生得分的中位数之和是 .?
解析:由茎叶图可知,甲的得分为17,22,23,28,34,35,36,其中位数为28;乙的得分为12,16,21,23,29,31,32,其中位数为23;所以甲、乙两名学生得分的中位数之和是51.
答案:51
4.已知某工厂在某年每月产品的总成本y(单位:万元)与该月产量x(单位:万件)之间的回归方程为y=1.215x+0.974,计算当x=2时,总成本y的估计值为 .?
解析:当x=2时,总成本y的估计值y=1.215×2+0.974=3.404.
答案:3.404探究一探究二探究三思维辨析当堂检测5.甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,你认为选派哪位学生参加比较合适?请说明理由.探究一探究二探究三思维辨析当堂检测 解:(1)作出茎叶图如下:
1.当总体容量较小,样本容量较小时,采用抽签法.
2.当总体容量较大,样本容量较小时,采用随机数法.
3.当总体容量较大,样本容量较大时,采用系统抽样法.
4.当总体由差异明显的几部分组成时,采用分层抽样法.
二、统计图表的特点与选择
1.若只需大致判断一些数据的分布规律,了解数据各元素所占比例的大小情况可以用扇形统计图;
2.若需要根据图表了解各个数据所占的频率可以使用条形统计图;
3.若要了解数据的增减情况可以采用折线图;
4.若要了解数据的全部信息可以用茎叶图.三、数据的数字特征
1.在样本数据中,出现次数最多的那个数据叫做众数.
2.将数据按大小排列,位于中间的数据(或中间两数的平均数)称为中位数.
3.平均数具有对数据进行“取齐”的作用,它代表了数据取值的平均水平,在频率分布直方图中,平均数是其平衡点.四、用样本估计总体
1.在频率分布直方图中,纵坐标的含义为 .
2.在频率分布直方图中,所有小长方形的面积和为1,每个小长方形的面积代表对应该组数据出现的频率.
3.频率分布折线图是把频率分布直方图中各个矩形上边的中点用线段连接起来而得到的,它不但可以表示出数量的多少,而且能清楚直观地表示数量增减的变化情况.
五、线性回归分析
1.变量与变量之间存在两种关系,一种确定性的关系为函数关系;另一种变量间确实存在关系,但带有随机性的为相关关系.
2.求线性回归方程的前提是两个变量具有线性相关关系,样本数据越多,变量间的相关程度越高,估计越精确.【做一做1】 下列四个图各反映了两个变量的某种关系,其中可以看作具有较强线性相关关系的是( )A.①③ B.①④ C.②③ D.①②
答案:B
【做一做2】 我校三个年级共有24个班,学校为了了解同学们的心理状况,将每个班级编号,依次为1到24,现用系统抽样方法,抽4个班进行调查,若抽到的编号之和为48,则抽到的最小编号为( )
A.2 B.3 C.4 D.5
解析:系统抽样的间隔为 ,设抽到的最小编号为x,则x+(6+x)+(12+x)+(18+x)=48,解得x=3,故选B.
答案:B 【做一做3】 已知某种产品的支出广告额x与利润额y(单位:万元)之间有如下对应数据:则回归直线必过( )
A.(5,36) B.(5,35) C.(5,30) D.(4,30)答案:A 【做一做4】 如图是一组样本数据的频率分布直方图,则依据图形中的数据,可以估计总体的平均数与中位数分别是( )
A.12.5,12.5
B.13,13
C.13.5,12.5
D.13.5,13
解析:根据频率分布直方图可以得到第一组的频率为0.2,第二组的频率为0.5,则第三组的频率为0.3,
则平均数为7.5×0.2+12.5×0.5+17.5×0.3=13,答案:B 【做一做5】 抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:则成绩较为稳定(方差较小)的那位运动员成绩的方差为 .?答案:2 探究一探究二探究三思维辨析当堂检测抽样方法的应用【例1】 问题:①某小区有800户家庭,其中高收入家庭200户,中等收入家庭480户,低收入家庭120户,为了了解有关家用轿车购买力的某个指标,要从中抽取一个容量为100的样本;②从10名学生中抽取3人参加座谈会.方法:(1)简单随机抽样;(2)系统抽样;(3)分层抽样.则问题与方法配对正确的是( )
A.①(1),②(2) B.①(3),②(2)
C.①(2),②(3) D.①(3),②(1)
解析:问题①中的总体是由差异明显的几部分组成的,故可采用分层抽样方法;问题②中总体的个数较少,故可采用简单随机抽样.故匹配正确的是D.
答案:D探究一探究二探究三思维辨析当堂检测反思感悟1.想要合理地选用抽样方法,需要明确各种抽样方法的特点及应用范围.
2.当问题中需要剔除某些个体的时候,也要“随机”,而不是“随便”.探究一探究二探究三思维辨析当堂检测 变式训练1某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的 ,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.探究一探究二探究三思维辨析当堂检测解:(1)设登山组人数为x,游泳组中青年人、中年人、老年人各占比例分别为a,b,c.探究一探究二探究三思维辨析当堂检测统计的基本思想及应用
【例2】 有一容量为200的样本,数据的分组以及各组的频数如下:
-20~-15,7;-15~-10,11;-10~-5,15;-5~0,40;0~5,
49;5~10,41;10~15,20;15~20,17.
(1)列出样本的频率分布表;
(2)画出频率分布直方图和频率分布折线图;
(3)求样本数据不足0的频率.探究一探究二探究三思维辨析当堂检测解:(1)频率分布表如下: 探究一探究二探究三思维辨析当堂检测(2)如图是频率分布直方图和频率分布折线图:
?
(3)样本数据不足0的频率为:
0.035+0.055+0.075+0.2=0.365.探究一探究二探究三思维辨析当堂检测反思感悟统计思想的应用技巧
1.用样本的频率分布估计总体分布时,绘制茎叶图、频率分布直方图等图形是关键,借助数形结合法易得到总体的分布情况.
2.计算样本的数字特征,如平均数、标准差等,根据样本的数据特点,正确地选用公式,采用简便的算法,从而估计出总体的数字特征,并对总体作出相应的估计.探究一探究二探究三思维辨析当堂检测 变式训练2某市一体校拟选拔一名帆船运动员参加省大学生运动会,对帆船运动员甲、乙两人在相同的条件下进行了6次测试,测得他们速度的数据如下:
甲:27,38,30,37,35,31;
乙:33,29,38,34,28,36.
(1)将这两组数据用茎叶图表示.
(2)根据题中数据,请你在甲、乙两人中确定参加省大学生运动会的帆船运动员,并说明理由.探究一探究二探究三思维辨析当堂检测 解:(1)由题意可得:这两组数据的茎叶图为: 探究一探究二探究三思维辨析当堂检测 线性回归分析及应用【例3】 某地连续十年粮食需求量逐年上升,下表是部分统计数据:
(1)利用所给数据求年需求量与年份之间的回归方程
(2)利用(1)中所求出的直线方程预测该地2020年的粮食需求量.
分析因为所给数据比较大,所以可以对数据进行初步处理,减少计算量.然后代入公式求解回归系数,利用回归直线方程预测时,也要注意数据的处理.探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测反思感悟线性回归是处理变量之间的线性相关关系的一种数理统计方法,它为生产、生活提供了一种科学的测算依据,如果两个变量线性相关,那么一定可以找到一条直线拟合该关系,关键是如何找出这样一条最佳拟合直线,即如何求得线性回归方程,利用线性回归方程对两个变量间的线性关系进行估计,实际上就是将非确定性的相关关系问题转化为确定性的函数关系进行研究,我们常用的方法就是“最小二乘法”,它使得样本数据的点到它的距离的平方和最小.探究一探究二探究三思维辨析当堂检测(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a.
(2)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.探究一探究二探究三思维辨析当堂检测未弄清频率分布直方图中数字特征的意义而致误
【典例】某城市100户居民的月平均用电量(单位:千瓦时),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数.探究一探究二探究三思维辨析当堂检测错解:(1)由(0.002+0.009 5+0.011+0.012 5+x+0.005+0.002 5)×20=1得x=0.007 5,
所以直方图中x的值是0.007 5.
(2)由众数的定义知,月平均用电量的众数是220~240.因为(0.002+0.009 5+0.011)×20=0.45<0.5,所以月平均用电量的中位数在[220,240)内,即为
正解:(1)由(0.002+0.009 5+0.011+0.012 5+x+0.005+0.002 5)×20=1,得x=0.007 5,
所以直方图中x的值是0.007 5.
(2)月平均用电量的众数是
因为(0.002+0.009 5+0.011)×20=0.45<0.5,所以月平均用电量的中位数在[220,240)内,设中位数为a,由(0.002+0.009 5+0.011)×20+0.012 5×(a-220)=0.5得a=224,所以月平均用电量的中位数是224.探究一探究二探究三思维辨析当堂检测纠错心得1.本题出现错误的根源是对频率分布直方图中的数字特征的意义理解不清,要知道,在频率分布直方图中众数是最高的矩形的底边中点的横坐标,是一个数,而不是范围.
2.在频率分布直方图中,中位数左右两侧直方图的面积相等,小矩形的高度代表的是对应该组数据 的值,只有明确了这些数据特征,才能做到有的放矢.探究一探究二探究三思维辨析当堂检测变式训练一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中用分层抽样方法抽出80人做进一步调查,则在[1 500,2 000)(元)月收入段应抽出 人.?探究一探究二探究三思维辨析当堂检测解:析:由频率分布直方图知,收入在1 500~2 000元之间的频率为0.000 4×500=0.2,所以在[1 500,2 000)(元)月收入段应抽出80×0.2=16(人).
答案:16探究一探究二探究三思维辨析当堂检测1.某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名,现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
A.6 B.8 C.10 D.12
解析:设从高二年级抽取的学生数为n,
答案:B探究一探究二探究三思维辨析当堂检测2.某产品的广告费用x与销售额y的统计数据如下表:根据上表可得回归方程y=bx+a中的b=10.6,据此模型预报广告费用为10万元时销售额为( )
A.112.1万元 B.113.1万元
C.113.9万元 D.111.9万元答案:D 探究一探究二探究三思维辨析当堂检测3.如图是某中学甲、乙两名学生2017年上半年篮球比赛每场比赛得分的茎叶图,则甲、乙两名学生得分的中位数之和是 .?
解析:由茎叶图可知,甲的得分为17,22,23,28,34,35,36,其中位数为28;乙的得分为12,16,21,23,29,31,32,其中位数为23;所以甲、乙两名学生得分的中位数之和是51.
答案:51
4.已知某工厂在某年每月产品的总成本y(单位:万元)与该月产量x(单位:万件)之间的回归方程为y=1.215x+0.974,计算当x=2时,总成本y的估计值为 .?
解析:当x=2时,总成本y的估计值y=1.215×2+0.974=3.404.
答案:3.404探究一探究二探究三思维辨析当堂检测5.甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,你认为选派哪位学生参加比较合适?请说明理由.探究一探究二探究三思维辨析当堂检测 解:(1)作出茎叶图如下:
