高中数学北师大版必修3课件:1.6 统计活动:结婚年龄的变化:24张PPT
文档属性
| 名称 | 高中数学北师大版必修3课件:1.6 统计活动:结婚年龄的变化:24张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 781.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 12:25:09 | ||
图片预览







文档简介
课件24张PPT。§6 统计活动:结婚年龄的变化统计活动的步骤
(1)明确调查的目的,确定调查的对象.
(2)利用随机抽样抽取样本,收集数据.
(3)整理数据,用表格来表示数据.
(4)分析数据,其方法有两种:一是用统计图表来分析,二是计算数据的数字特征.
(5)作出推断,通过分析数据作出推断.
【做一做】 给出统计活动的5个步骤,则它们之间正确的顺序是( )
①收集数据 ②整理数据 ③确定调查对象
④分析数据 ⑤作出推断
A.①②③④⑤ B.③①②④⑤
C.③①②⑤④ D.①③②⑤④
答案:B思考辨析
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)统计活动中,调查的对象要按随机的原则选取,要保证总体中每一个被调查对象被选取的机会均等. ( )
(2)统计活动中,整理数据一般采用表格法整理. ( )
(3)确定调查对象时要保证使样本的选取具有代表性,不能出现倾向性误差. ( )
(4)为了调查我国山区老百姓的生活水平,应采用普查的方式. ( )
答案:(1)√ (2)√ (3)√ (4)×探究一探究二思想方法当堂检测统计方案的制定和数据的收集
【例1】 (1)有以下调查项目:
①在中学生中,喜欢写作的学生所占的比例.
②“五一”期间,乘坐火车的人比平时多很多,铁路部门要了解旅客是否都是购票乘车的.
③开学前夕,电工检查学校的照明灯是否正常工作.
④全国观众对中央电视台“春节联欢晚会”的满意程度.适合用普查的是 ,适合用抽样调查的是 .?
(2)国务院召开全国青少年校园足球工作电视电话会议,将足球纳入我国学校体育课程教学体系,作为体育课必修内容,为学生提供学习足球的机会.中国业余足球迎来了前所未有的最好发展时期.
请设计一个统计方案,估计你所在的县市的中学生中,喜欢足球的学生所占比例的大小,写出主要步骤.探究一探究二思想方法当堂检测(1)解析:①④适宜抽样调查,②③适宜普查.
答案:②③ ①④
(2)解:可以按照如下的步骤来进行这个统计活动.
①确定调查的对象:该县市的全体中学生;
明确调查的目的:是否喜欢足球运动.
②利用随机抽样抽取样本,收集数据.由于中学生太多,只能进行抽样调查.由于学校之间存在差别,采用分层抽样在各个中学抽取样本.为了统计的方便,设计如下的调查表,记录下来.最好和你的同学一起完成收集数据的任务. 探究一探究二思想方法当堂检测③整理数据,用表格来表示数据.
把所收集到的数据汇总成一个表格,如表:④分析数据.
由于是调查喜欢足球的学生占多大的百分比,因此选用扇形统计图来表示.
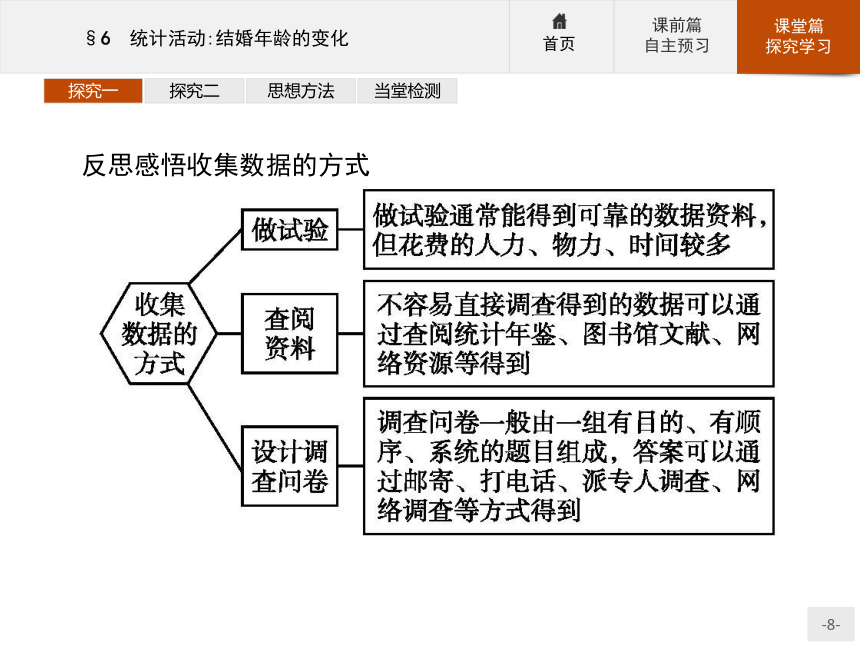
⑤作出推断,通过分析数据作出推断.根据扇形统计图作出推断.探究一探究二思想方法当堂检测反思感悟收集数据的方式 探究一探究二思想方法当堂检测变式训练1请你设计一个调查全校同学喜欢球类情况的试验.
解:试验的设计步骤如下:
(1)明确目的,准备人手.
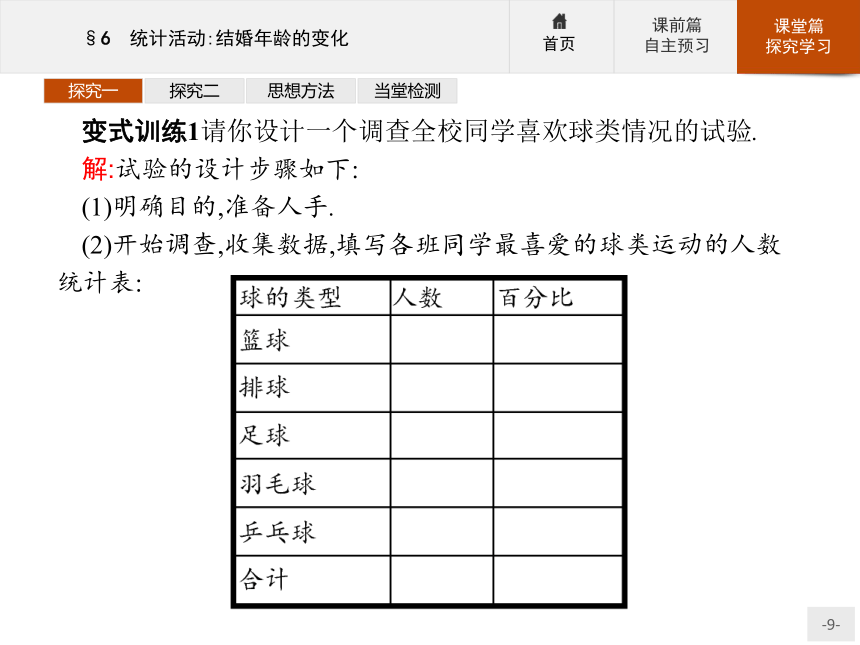
(2)开始调查,收集数据,填写各班同学最喜爱的球类运动的人数统计表:探究一探究二思想方法当堂检测(3)分析数据,让学生针对统计表得出的数据进行分析,为了更直观地看出表中的信息,还可以用条形统计图和扇形统计图来描述数据.
(4)作出推断,形成报告.探究一探究二思想方法当堂检测统计活动中的数据分析
【例2】 某学校高一(1)班和高一(2)班各有49名学生,两班在一次数学测验中的成绩统计如下:(1)请你对下面的一段话给予简要分析:
(1)班的小刚回家对妈妈说:“昨天的数学测验,全班平均分79分,得70分的人最多,我得了85分,在班里算是上游了!”
(2)请你根据表中的数据,对这两个班的数学测验情况进行简要分析,并提出建议.探究一探究二思想方法当堂检测解:(1)由于(1)班49名学生数学测验成绩的中位数是87,则85分排在全班第25名之后,所以从位次上看,不能说85分是上游,成绩应该属于中游.但也不能以位次来判断学习的好坏,小刚得了85分,说明他对这段的学习内容掌握得较好,从掌握学习的内容上讲,也可以说属于上游.
(2)(1)班的成绩的中位数是87分,说明不低于87分(含87分)的人数占一半以上,而平均分为79分,标准差又很大,说明低分也多,两极分化严重,建议加强对学习困难的学生的帮助.
(2)班的中位数和平均数都是79分,标准差又小,说明学生之间差别较小,学习很差的学生少,但学习优异的也很少,建议采取措施提高优秀率.探究一探究二思想方法当堂检测反思感悟1.统计活动中的数据分析,可以分析数据中的数字特征,从而全面把握总体情况.
2.统计活动中的数据分析,可以采取图表来分析.这样得到的结果更直观,更能体现出各部分所占的份额.
3.根据统计活动作出的推断结论的准确性,取决于抽取的样本是否具有代表性以及样本容量的大小.一般来说,用科学的抽样方法抽取样本,并且样本容量足够大,由这样的统计活动得到的结论准确性高,可信度大,可以作为决策的依据.探究一探究二思想方法当堂检测变式训练2某中学人数相等的甲、乙两班学生参加同一次数学测试,两班平均分和方差分别为
则成绩较为整齐的是( )
A.甲班 B.乙班
C.两班一样齐 D.无法确定
答案:B探究一探究二思想方法当堂检测统计在实际问题中的应用
【典例】在美国历届总统中,就任时年纪最小的是罗斯福,他于1901年就任,当时年仅42岁;就任时年纪最大的是里根,他于1981年就任,当时69岁.下面按时间顺序(从1789年的华盛顿到2009年的奥巴马,共44任)给出了历届美国总统就任时的年龄:
57,61,57,57,58,57,61,54,68,51,49,64,50,48,65,52,56,46,54,49,51,47,55,55,54,42,51,56,55,51,54,51,60,62,43,55,56,61,52,69,64,46,54,48
(1)将数据进行适当的分组,并画出相应的频率分布直方图和频率分布折线图;
(2)用自己的语言描述一下历届美国总统就任时年龄的分布情况.
思路点拨:画出频率分布直方图的前提是先给出频率分布表.探究一探究二思想方法当堂检测解:(1)以4为组距,列表如下: 探究一探究二思想方法当堂检测相应的频率分布直方图和频率分布折线图如图:(2)从频率分布表中可以看出,将近65%的美国总统就任时的年龄在50岁至60岁之间,45岁以下以及65岁以上就任的总统所占的比例相对较小.探究一探究二思想方法当堂检测方法点睛利用频率分布直方图与频率分布折线图解决实际问题时要注意:
(1)绘图时,应以横轴表示分组,纵轴表示各组频率与组距的比值,以各个组距为底,以各频率除以组距的商为高,分别画成矩形,便得到频率分布直方图;
(2)在频率分布直方图左右两边各添加一个区间,顺次连接频率分布直方图中各个矩形上边的中点及左右两边区间的中点,就得到频率分布折线图.探究一探究二思想方法当堂检测变式训练某学校随机抽取20个班,调查各班中有网上购物经历的人数,所得数据的茎叶图如图所示.以组距为5将数据分组成[0,5),[5,10),…,[30,35),[35,40]时,所作的频率分布直方图是( )探究一探究二思想方法当堂检测解析:根据题意,由频率与频数的关系,计算可得各组的频率,进而可以作出频率分布表,结合频率分布表,进而可以作出频率分布直方图.根据题意,可得频率分布表:进而可以作频率分布直方图,分析可知选A.
答案:A探究一探究二思想方法当堂检测1.下面是四位同学对他们学习小组将要共同进行的一次统计活动分别设计的活动程序,其中正确的是( )答案:C
2.为了调查2017年上半年我国居民消费价格指数的变化情况,收集数据后,整理、分析数据的最佳方式是( )
A.画茎叶图 B.画扇形统计图
C.画折线统计图 D.计算方差
答案:C探究一探究二思想方法当堂检测3.如图所示是容量为100的样本的频率分布直方图,试根据图形中的数据填空:
(1)样本数据落在范围[6,10)内的频率为 ;?
(2)样本数据落在范围[10,14)内的频数为 ;?
(3)总体在[2,6)内的频率约为 .?
解析:(1)样本数据落在范围[6,10)内的频率为0.08×4=0.32;
(2)样本数据落在范围[10,14)内的频数为0.09×4×100=36;
(3)总体在[2,6)内的频率约为0.02×4=0.08.
答案:(1)0.32 (2)36 (3)0.08探究一探究二思想方法当堂检测4.问题情境:湖南卫视推出的户外真人秀节目《爸爸去哪儿》在儿童观众中引起强烈反响,获得了很高的关注度和收视率.
问题:请设计统计方案,估计你所在市(县)的小学生中,喜欢《爸爸去哪儿》这个节目的学生所占的比例.
解:可以按照如下的步骤来进行这个统计活动:
(1)确定调查的对象:该县(市)的全体小学生;明确调查的目的:是否喜欢《爸爸去哪儿》这个节目.
(2)利用随机抽样抽取样本,收集数据.
由于一个县(市)的小学生太多,只能进行抽样调查.由于学校之间存在差别,采用分层抽样在各个小学抽取样本.为了统计的方便,设计如下的调查表,记录下来.最好你和你的同学一起完成收集数据的任务.探究一探究二思想方法当堂检测(3)整理数据,用表格来表示数据.
把所收集到的数据汇总成一个表格,如下表.(4)分析数据.
由于是调查喜欢这个节目的学生所占的百分比,因此选用扇形统计图来表示.
(5)作出推断.通过分析数据作出推断.
根据扇形统计图作出推断.
(1)明确调查的目的,确定调查的对象.
(2)利用随机抽样抽取样本,收集数据.
(3)整理数据,用表格来表示数据.
(4)分析数据,其方法有两种:一是用统计图表来分析,二是计算数据的数字特征.
(5)作出推断,通过分析数据作出推断.
【做一做】 给出统计活动的5个步骤,则它们之间正确的顺序是( )
①收集数据 ②整理数据 ③确定调查对象
④分析数据 ⑤作出推断
A.①②③④⑤ B.③①②④⑤
C.③①②⑤④ D.①③②⑤④
答案:B思考辨析
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)统计活动中,调查的对象要按随机的原则选取,要保证总体中每一个被调查对象被选取的机会均等. ( )
(2)统计活动中,整理数据一般采用表格法整理. ( )
(3)确定调查对象时要保证使样本的选取具有代表性,不能出现倾向性误差. ( )
(4)为了调查我国山区老百姓的生活水平,应采用普查的方式. ( )
答案:(1)√ (2)√ (3)√ (4)×探究一探究二思想方法当堂检测统计方案的制定和数据的收集
【例1】 (1)有以下调查项目:
①在中学生中,喜欢写作的学生所占的比例.
②“五一”期间,乘坐火车的人比平时多很多,铁路部门要了解旅客是否都是购票乘车的.
③开学前夕,电工检查学校的照明灯是否正常工作.
④全国观众对中央电视台“春节联欢晚会”的满意程度.适合用普查的是 ,适合用抽样调查的是 .?
(2)国务院召开全国青少年校园足球工作电视电话会议,将足球纳入我国学校体育课程教学体系,作为体育课必修内容,为学生提供学习足球的机会.中国业余足球迎来了前所未有的最好发展时期.
请设计一个统计方案,估计你所在的县市的中学生中,喜欢足球的学生所占比例的大小,写出主要步骤.探究一探究二思想方法当堂检测(1)解析:①④适宜抽样调查,②③适宜普查.
答案:②③ ①④
(2)解:可以按照如下的步骤来进行这个统计活动.
①确定调查的对象:该县市的全体中学生;
明确调查的目的:是否喜欢足球运动.
②利用随机抽样抽取样本,收集数据.由于中学生太多,只能进行抽样调查.由于学校之间存在差别,采用分层抽样在各个中学抽取样本.为了统计的方便,设计如下的调查表,记录下来.最好和你的同学一起完成收集数据的任务. 探究一探究二思想方法当堂检测③整理数据,用表格来表示数据.
把所收集到的数据汇总成一个表格,如表:④分析数据.
由于是调查喜欢足球的学生占多大的百分比,因此选用扇形统计图来表示.
⑤作出推断,通过分析数据作出推断.根据扇形统计图作出推断.探究一探究二思想方法当堂检测反思感悟收集数据的方式 探究一探究二思想方法当堂检测变式训练1请你设计一个调查全校同学喜欢球类情况的试验.
解:试验的设计步骤如下:
(1)明确目的,准备人手.
(2)开始调查,收集数据,填写各班同学最喜爱的球类运动的人数统计表:探究一探究二思想方法当堂检测(3)分析数据,让学生针对统计表得出的数据进行分析,为了更直观地看出表中的信息,还可以用条形统计图和扇形统计图来描述数据.
(4)作出推断,形成报告.探究一探究二思想方法当堂检测统计活动中的数据分析
【例2】 某学校高一(1)班和高一(2)班各有49名学生,两班在一次数学测验中的成绩统计如下:(1)请你对下面的一段话给予简要分析:
(1)班的小刚回家对妈妈说:“昨天的数学测验,全班平均分79分,得70分的人最多,我得了85分,在班里算是上游了!”
(2)请你根据表中的数据,对这两个班的数学测验情况进行简要分析,并提出建议.探究一探究二思想方法当堂检测解:(1)由于(1)班49名学生数学测验成绩的中位数是87,则85分排在全班第25名之后,所以从位次上看,不能说85分是上游,成绩应该属于中游.但也不能以位次来判断学习的好坏,小刚得了85分,说明他对这段的学习内容掌握得较好,从掌握学习的内容上讲,也可以说属于上游.
(2)(1)班的成绩的中位数是87分,说明不低于87分(含87分)的人数占一半以上,而平均分为79分,标准差又很大,说明低分也多,两极分化严重,建议加强对学习困难的学生的帮助.
(2)班的中位数和平均数都是79分,标准差又小,说明学生之间差别较小,学习很差的学生少,但学习优异的也很少,建议采取措施提高优秀率.探究一探究二思想方法当堂检测反思感悟1.统计活动中的数据分析,可以分析数据中的数字特征,从而全面把握总体情况.
2.统计活动中的数据分析,可以采取图表来分析.这样得到的结果更直观,更能体现出各部分所占的份额.
3.根据统计活动作出的推断结论的准确性,取决于抽取的样本是否具有代表性以及样本容量的大小.一般来说,用科学的抽样方法抽取样本,并且样本容量足够大,由这样的统计活动得到的结论准确性高,可信度大,可以作为决策的依据.探究一探究二思想方法当堂检测变式训练2某中学人数相等的甲、乙两班学生参加同一次数学测试,两班平均分和方差分别为
则成绩较为整齐的是( )
A.甲班 B.乙班
C.两班一样齐 D.无法确定
答案:B探究一探究二思想方法当堂检测统计在实际问题中的应用
【典例】在美国历届总统中,就任时年纪最小的是罗斯福,他于1901年就任,当时年仅42岁;就任时年纪最大的是里根,他于1981年就任,当时69岁.下面按时间顺序(从1789年的华盛顿到2009年的奥巴马,共44任)给出了历届美国总统就任时的年龄:
57,61,57,57,58,57,61,54,68,51,49,64,50,48,65,52,56,46,54,49,51,47,55,55,54,42,51,56,55,51,54,51,60,62,43,55,56,61,52,69,64,46,54,48
(1)将数据进行适当的分组,并画出相应的频率分布直方图和频率分布折线图;
(2)用自己的语言描述一下历届美国总统就任时年龄的分布情况.
思路点拨:画出频率分布直方图的前提是先给出频率分布表.探究一探究二思想方法当堂检测解:(1)以4为组距,列表如下: 探究一探究二思想方法当堂检测相应的频率分布直方图和频率分布折线图如图:(2)从频率分布表中可以看出,将近65%的美国总统就任时的年龄在50岁至60岁之间,45岁以下以及65岁以上就任的总统所占的比例相对较小.探究一探究二思想方法当堂检测方法点睛利用频率分布直方图与频率分布折线图解决实际问题时要注意:
(1)绘图时,应以横轴表示分组,纵轴表示各组频率与组距的比值,以各个组距为底,以各频率除以组距的商为高,分别画成矩形,便得到频率分布直方图;
(2)在频率分布直方图左右两边各添加一个区间,顺次连接频率分布直方图中各个矩形上边的中点及左右两边区间的中点,就得到频率分布折线图.探究一探究二思想方法当堂检测变式训练某学校随机抽取20个班,调查各班中有网上购物经历的人数,所得数据的茎叶图如图所示.以组距为5将数据分组成[0,5),[5,10),…,[30,35),[35,40]时,所作的频率分布直方图是( )探究一探究二思想方法当堂检测解析:根据题意,由频率与频数的关系,计算可得各组的频率,进而可以作出频率分布表,结合频率分布表,进而可以作出频率分布直方图.根据题意,可得频率分布表:进而可以作频率分布直方图,分析可知选A.
答案:A探究一探究二思想方法当堂检测1.下面是四位同学对他们学习小组将要共同进行的一次统计活动分别设计的活动程序,其中正确的是( )答案:C
2.为了调查2017年上半年我国居民消费价格指数的变化情况,收集数据后,整理、分析数据的最佳方式是( )
A.画茎叶图 B.画扇形统计图
C.画折线统计图 D.计算方差
答案:C探究一探究二思想方法当堂检测3.如图所示是容量为100的样本的频率分布直方图,试根据图形中的数据填空:
(1)样本数据落在范围[6,10)内的频率为 ;?
(2)样本数据落在范围[10,14)内的频数为 ;?
(3)总体在[2,6)内的频率约为 .?
解析:(1)样本数据落在范围[6,10)内的频率为0.08×4=0.32;
(2)样本数据落在范围[10,14)内的频数为0.09×4×100=36;
(3)总体在[2,6)内的频率约为0.02×4=0.08.
答案:(1)0.32 (2)36 (3)0.08探究一探究二思想方法当堂检测4.问题情境:湖南卫视推出的户外真人秀节目《爸爸去哪儿》在儿童观众中引起强烈反响,获得了很高的关注度和收视率.
问题:请设计统计方案,估计你所在市(县)的小学生中,喜欢《爸爸去哪儿》这个节目的学生所占的比例.
解:可以按照如下的步骤来进行这个统计活动:
(1)确定调查的对象:该县(市)的全体小学生;明确调查的目的:是否喜欢《爸爸去哪儿》这个节目.
(2)利用随机抽样抽取样本,收集数据.
由于一个县(市)的小学生太多,只能进行抽样调查.由于学校之间存在差别,采用分层抽样在各个小学抽取样本.为了统计的方便,设计如下的调查表,记录下来.最好你和你的同学一起完成收集数据的任务.探究一探究二思想方法当堂检测(3)整理数据,用表格来表示数据.
把所收集到的数据汇总成一个表格,如下表.(4)分析数据.
由于是调查喜欢这个节目的学生所占的百分比,因此选用扇形统计图来表示.
(5)作出推断.通过分析数据作出推断.
根据扇形统计图作出推断.
