高中数学人教A版选修4-1课件:本讲整合2 :38张PPT
文档属性
| 名称 | 高中数学人教A版选修4-1课件:本讲整合2 :38张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 12:31:06 | ||
图片预览










文档简介
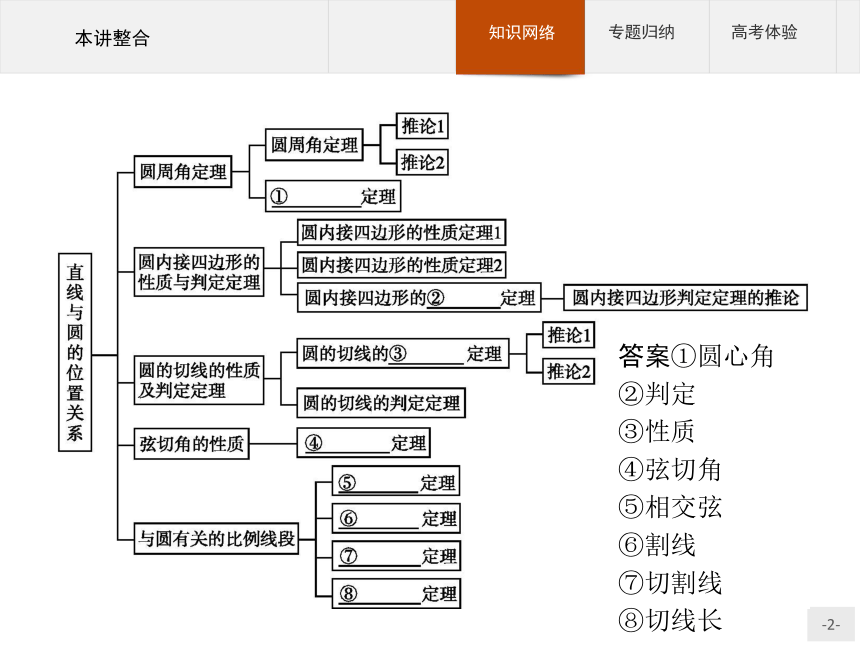
课件38张PPT。本讲整合答案①圆心角
②判定
③性质
④弦切角
⑤相交弦
⑥割线
⑦切割线
⑧切线长专题一专题二专题一:与圆有关的角的计算与证明
圆中的角有三类:圆心角、圆周角、弦切角,圆中有关角的计算和证明问题多与这三类角有关,因此圆心角定理、圆周角定理、弦切角定理是解决这类问题的知识基础,求解这类问题时,通常利用圆心角、圆周角、弦切角以及圆弧之间的关系来进行转化,求解中注意运用圆内接四边形的对角互补等性质.专题一专题二例1如图,锐角三角形ABC内接于☉O,∠ABC=60°,∠BAC=40°,作OE⊥AB交劣弧 于点E,连接EC,则∠OEC=( )
A.5° B.10° C.15° D.20°专题一专题二专题一专题二变式训练1 如图所示,四边形ABCD是☉O的内接四边形,延长BC到E,若∠BCD∶∠ECD=3∶2,则∠BOD等于( )?
A.120° B.136° C.144° D.150°
解析由∠BCD∶∠ECD=3∶2,可得∠ECD=72°.由圆内接四边形的性质知∠A=∠DCE,所以∠A=72°,故∠BOD=2∠A=144°.
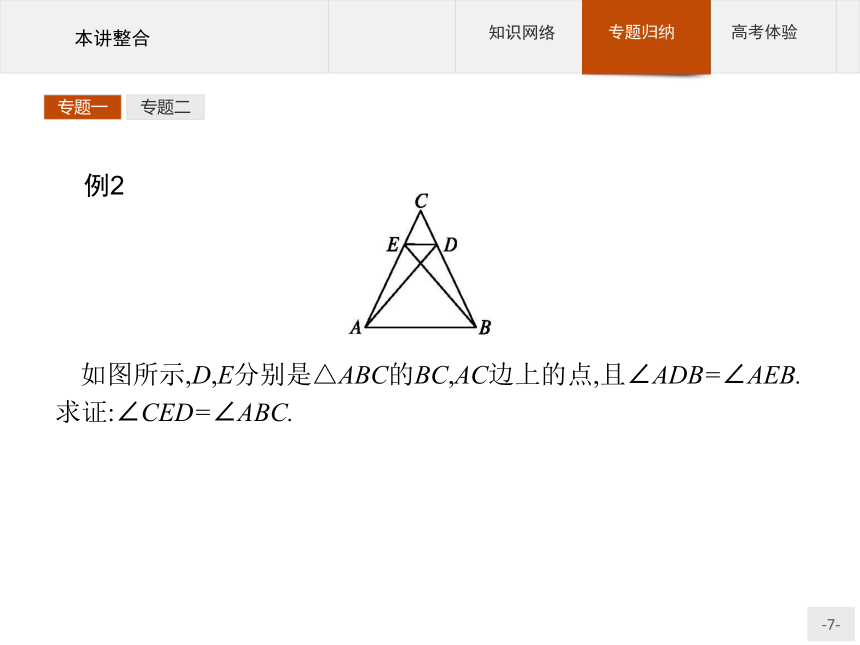
答案C专题一专题二例2
如图所示,D,E分别是△ABC的BC,AC边上的点,且∠ADB=∠AEB.求证:∠CED=∠ABC.
分析要证明∠CED=∠ABC,容易想到圆内接四边形的性质,需证A,B,D,E四点共圆.用圆内接四边形的判定定理不易找到条件,故采用分类讨论来解决.专题一专题二证明作△ABE的外接圆,则点D与外接圆有三种位置关系:①点D在圆外;②点D在圆内;③点D在圆上.
(1)如果点D在圆外,设BD与圆交于点F,连接AF,如图所示.
则∠AFB=∠AEB.而∠AEB=∠ADB,
∴∠AFB=∠ADB.
这与“三角形的外角大于任一不相邻的内角”矛盾.
故点D不能在圆外.专题一专题二(2)如果点D在圆内,设圆与BD的延长线交于F,连接AF,如图所示,
则∠AFB=∠AEB.
又∵∠AEB=∠ADB,
∴∠AFB=∠ADB.
这也与“三角形的外角大于任一不相邻的内角”矛盾.
故点D不可能在圆内.
综上可得,点A,B,D,E在同一圆上.
∴∠CED=∠ABC.专题一专题二变式训练2?
如图,AB是圆O的直径,C,D是圆O上位于AB异侧的两点.求证:∠OCB=∠D.
证明因为B,C是圆O上的两点,所以OB=OC,故∠OCB=∠B.
又因为C,D是圆O上位于AB异侧的两点,所以∠B,∠D为同弧所对的两个圆周角,所以∠B=∠D,因此∠OCB=∠D.专题一专题二专题二:与圆有关的线段的计算与证明
解决与圆有关的线段的计算与证明问题时,首先要考虑利用相交弦定理、割线定理、切割线定理、切线长定理等,由此获得成比例的线段或相等的线段,再结合直角三角形中的射影定理、相似三角形的性质等进行等比例代换或等线段代换,从而证得结论,或者建立方程(组),求得未知线段.专题一专题二例3
如图,A,B是两圆的交点,AC是小圆的直径,D和E分别是CA和CB的延长线与大圆的交点,已知AC=4,BE=10,且CB=AD,求DE的长.
分析先由割线定理求出CB的长度,从而得出CD,CE的长度,再证明△CDE为直角三角形,利用勾股定理求得DE.专题一专题二解
设CB=AD=x,则由割线定理得CA·CD=CB·CE,即4(4+x)=x(x+10),
化简得x2+6x-16=0,解得x=2或x=-8(舍去),从而CD=4+2=6,CE=2+10=12.
连接AB,因为CA为小圆的直径,所以∠CBA=90°,即∠ABE=90°,
则由圆的内接四边形对角互补,得∠D=90°,即△CDE是直角专题一专题二专题一专题二变式训练3 如图,AT切☉O于T,若AT=6,AE=3,AD=4,DE=2,则BC等于( )?
A.3 B.4 C.6 D.8
解析∵AT为☉O的切线,∴AT2=AD·AC.
又∵AT=6,AD=4,∴AC=9.
∵∠ADE=∠B,∠EAD=∠CAB,
∴△EAD∽△CAB,
答案C专题一专题二例4
如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点,且PG=PD,连接DG并延长交圆于点A,作弦AB⊥EP,垂足为F.
(1)求证:AB为圆的直径;
(2)若AC=BD,求证:AB=ED.
分析对于(1),可利用弦切角与圆周角的关系及等腰三角形的底角相等证∠BDA=90°.对于(2),应先证明△BDA≌△ACB,再证明∠DCE=90°即可.专题一专题二证明(1)因为PD=PG,所以∠PDG=∠PGD.
由于PD为切线,故∠PDA=∠DBA.
又由于∠PGD=∠EGA,故∠DBA=∠EGA,
所以∠DBA+∠BAD=∠EGA+∠BAD,
从而∠BDA=∠PFA.
因为AF⊥EP,所以∠PFA=90°,于是∠BDA=90°,
故AB是圆的直径.(2)连接BC,DC.由于AB是直径,故∠BDA=∠ACB=90°.
在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,
从而Rt△BDA≌Rt△ACB,于是∠DAB=∠CBA.
又因为∠DCB=∠DAB,所以∠DCB=∠CBA,故DC∥AB.因为AB⊥EP,所以DC⊥EP,∠DCE为直角,于是ED为直径.
由于AB和ED都是圆的直径,故ED=AB.专题一专题二专题一专题二变式训练4?
如图,点A为圆外一点,过点A作圆的两条切线,切点分别为B,C,ADE是圆的割线,连接CD,BD,BE,CE.
(1)求证:BE·CD=BD·CE;
(2)延长CD交AB于点F,若CE∥AB,证明:F为线段AB的中点.专题一专题二考点1考点2考点3考点4考点1:圆周角问题
1.
(2016·全国丙高考)如图,☉O中 的中点为P,弦PC,PD分别交AB于E,F两点.
(1)若∠PFB=2∠PCD,求∠PCD的大小;
(2)若EC的垂直平分线与FD的垂直平分线交于点G,证明OG⊥CD.考点1考点2考点3考点4解(1)连接PB,BC,
则∠BFD=∠PBA+∠BPD,∠PCD=∠PCB+∠BCD.
所以∠PBA=∠PCB.
又∠BPD=∠BCD,
所以∠BFD=∠PCD.
又∠PFB+∠BFD=180°,∠PFB=2∠PCD,
所以3∠PCD=180°,因此∠PCD=60°.考点1考点2考点3考点4(2)因为∠PCD=∠BFD,所以∠EFD+∠PCD=180°,
由此知C,D,F,E四点共圆,其圆心既在CE的垂直平分线上,又在DF的垂直平分线上,故G就是过C,D,F,E四点的圆的圆心,
所以G在CD的垂直平分线上.
又O也在CD的垂直平分线上,因此OG⊥CD.考点1考点2考点3考点42.(2013·课标全国Ⅰ高考)
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
(1)证明:DB=DC;
(2)设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.考点1考点2考点3考点4(1)证明
连接DE,交BC于点G.
由弦切角定理得,∠ABE=∠BCE.
而∠ABE=∠CBE,故∠CBE=∠BCE,BE=CE.
又因为DB⊥BE,
所以DE为直径,∠DCE=90°,
由勾股定理可得DB=DC.考点1考点2考点3考点4考点2:圆内接四边形问题
3.(2015·湖南高考)如图,在☉O中,相交于点E的两弦AB,CD的中点分别是M,N.直线MO与直线CD相交于点F.证明:
(1)∠MEN+∠NOM=180°;
(2)FE·FN=FM·FO.考点1考点2考点3考点4证明
(1)如图所示,因为M,N分别是弦AB,CD的中点,所以OM⊥AB,ON⊥CD,即∠OME=90°,∠ENO=90°,因此∠OME+∠ENO=180°.
又四边形的内角和等于360°,故∠MEN+∠NOM=180°.
(2)由(1)知,O,M,E,N四点共圆,故由割线定理即得FE·FN=FM·FO.考点1考点2考点3考点44.(2016·全国乙高考)
如图,△OAB是等腰三角形,∠AOB=120°,以O为圆心, OA为半径作圆.
(1)证明:直线AB与☉O相切;
(2)点C,D在☉O上,且A,B,C,D四点共圆,证明:AB∥CD.考点1考点2考点3考点4解(1)设E是AB的中点,连接OE.
因为OA=OB,∠AOB=120°,
所以OE⊥AB,∠AOE=60°.
在Rt△AOE中,OE= AO,即O到直线AB的距离等于☉O半径,所以直线AB与☉O相切.
(2)因为OA=2OD,所以O不是A,B,C,D四点所在圆的圆心.
设O'是A,B,C,D四点所在圆的圆心,作直线OO'.
由已知得O在线段AB的垂直平分线上,
又O'在线段AB的垂直平分线上,所以OO'⊥AB.
同理可证,OO'⊥CD.所以AB∥CD.考点1考点2考点3考点4考点3:切割线问题
5.(2016·天津高考)如图,AB是圆的直径,弦CD与AB相交于点E,BE=2AE=2,BD=ED,则线段CE的长为 .?考点1考点2考点3考点4考点1考点2考点3考点46.(2015·重庆高考)如图,圆O的弦AB,CD相交于
点E,过点A作圆O的切线与DC的延长线交于
点P,若PA=6,AE=9,PC=3,CE∶ED=2∶1,
则BE= .?
解析因为PA是圆的切线,所以有PA2=PC·PD,
因此CD=PD-PC=9.
又因为CE∶ED=2∶1,所以CE=6,ED=3.
又由相交弦定理可得AE·BE=CE·ED,
答案2考点1考点2考点3考点4考点1考点2考点3考点4考点4:切线问题
8.(2015·广东高考)如图,已知AB是圆O的直径,AB=4,EC是圆O的切线,切点为C,BC=1,过圆心O作BC的平行线,分别交EC和AC于点D和点P,则OD= .?考点1考点2考点3考点4考点1考点2考点3考点49.(2013·重庆高考)如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则DE的长为 .?
解析在Rt△ABC中,∠A=60°,AB=20,可得BC=10
由弦切角定理,可得∠BCD=∠A=60°.
在Rt△BCD中,可求得CD=5 ,BD=15.
又由切割线定理,可得CD2=DE·DB,可求得DE=5.
答案5考点1考点2考点3考点410.(2015·课标全国Ⅰ高考)
如图,AB是☉O的直径,AC是☉O的切线,BC交☉O于点E.
(1)若D为AC的中点,证明:DE是☉O的切线;
(2)若OA= CE,求∠ACB的大小.考点1考点2考点3考点4解(1)连接AE,由已知得,AE⊥BC,AC⊥AB.
在Rt△AEC中,由已知得,DE=DC,
故∠DEC=∠DCE.
连接OE,则∠OBE=∠OEB.
又∠ACB+∠ABC=90°,
所以∠DEC+∠OEB=90°,
故∠OED=90°,DE是☉O的切线.
②判定
③性质
④弦切角
⑤相交弦
⑥割线
⑦切割线
⑧切线长专题一专题二专题一:与圆有关的角的计算与证明
圆中的角有三类:圆心角、圆周角、弦切角,圆中有关角的计算和证明问题多与这三类角有关,因此圆心角定理、圆周角定理、弦切角定理是解决这类问题的知识基础,求解这类问题时,通常利用圆心角、圆周角、弦切角以及圆弧之间的关系来进行转化,求解中注意运用圆内接四边形的对角互补等性质.专题一专题二例1如图,锐角三角形ABC内接于☉O,∠ABC=60°,∠BAC=40°,作OE⊥AB交劣弧 于点E,连接EC,则∠OEC=( )
A.5° B.10° C.15° D.20°专题一专题二专题一专题二变式训练1 如图所示,四边形ABCD是☉O的内接四边形,延长BC到E,若∠BCD∶∠ECD=3∶2,则∠BOD等于( )?
A.120° B.136° C.144° D.150°
解析由∠BCD∶∠ECD=3∶2,可得∠ECD=72°.由圆内接四边形的性质知∠A=∠DCE,所以∠A=72°,故∠BOD=2∠A=144°.
答案C专题一专题二例2
如图所示,D,E分别是△ABC的BC,AC边上的点,且∠ADB=∠AEB.求证:∠CED=∠ABC.
分析要证明∠CED=∠ABC,容易想到圆内接四边形的性质,需证A,B,D,E四点共圆.用圆内接四边形的判定定理不易找到条件,故采用分类讨论来解决.专题一专题二证明作△ABE的外接圆,则点D与外接圆有三种位置关系:①点D在圆外;②点D在圆内;③点D在圆上.
(1)如果点D在圆外,设BD与圆交于点F,连接AF,如图所示.
则∠AFB=∠AEB.而∠AEB=∠ADB,
∴∠AFB=∠ADB.
这与“三角形的外角大于任一不相邻的内角”矛盾.
故点D不能在圆外.专题一专题二(2)如果点D在圆内,设圆与BD的延长线交于F,连接AF,如图所示,
则∠AFB=∠AEB.
又∵∠AEB=∠ADB,
∴∠AFB=∠ADB.
这也与“三角形的外角大于任一不相邻的内角”矛盾.
故点D不可能在圆内.
综上可得,点A,B,D,E在同一圆上.
∴∠CED=∠ABC.专题一专题二变式训练2?
如图,AB是圆O的直径,C,D是圆O上位于AB异侧的两点.求证:∠OCB=∠D.
证明因为B,C是圆O上的两点,所以OB=OC,故∠OCB=∠B.
又因为C,D是圆O上位于AB异侧的两点,所以∠B,∠D为同弧所对的两个圆周角,所以∠B=∠D,因此∠OCB=∠D.专题一专题二专题二:与圆有关的线段的计算与证明
解决与圆有关的线段的计算与证明问题时,首先要考虑利用相交弦定理、割线定理、切割线定理、切线长定理等,由此获得成比例的线段或相等的线段,再结合直角三角形中的射影定理、相似三角形的性质等进行等比例代换或等线段代换,从而证得结论,或者建立方程(组),求得未知线段.专题一专题二例3
如图,A,B是两圆的交点,AC是小圆的直径,D和E分别是CA和CB的延长线与大圆的交点,已知AC=4,BE=10,且CB=AD,求DE的长.
分析先由割线定理求出CB的长度,从而得出CD,CE的长度,再证明△CDE为直角三角形,利用勾股定理求得DE.专题一专题二解
设CB=AD=x,则由割线定理得CA·CD=CB·CE,即4(4+x)=x(x+10),
化简得x2+6x-16=0,解得x=2或x=-8(舍去),从而CD=4+2=6,CE=2+10=12.
连接AB,因为CA为小圆的直径,所以∠CBA=90°,即∠ABE=90°,
则由圆的内接四边形对角互补,得∠D=90°,即△CDE是直角专题一专题二专题一专题二变式训练3 如图,AT切☉O于T,若AT=6,AE=3,AD=4,DE=2,则BC等于( )?
A.3 B.4 C.6 D.8
解析∵AT为☉O的切线,∴AT2=AD·AC.
又∵AT=6,AD=4,∴AC=9.
∵∠ADE=∠B,∠EAD=∠CAB,
∴△EAD∽△CAB,
答案C专题一专题二例4
如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点,且PG=PD,连接DG并延长交圆于点A,作弦AB⊥EP,垂足为F.
(1)求证:AB为圆的直径;
(2)若AC=BD,求证:AB=ED.
分析对于(1),可利用弦切角与圆周角的关系及等腰三角形的底角相等证∠BDA=90°.对于(2),应先证明△BDA≌△ACB,再证明∠DCE=90°即可.专题一专题二证明(1)因为PD=PG,所以∠PDG=∠PGD.
由于PD为切线,故∠PDA=∠DBA.
又由于∠PGD=∠EGA,故∠DBA=∠EGA,
所以∠DBA+∠BAD=∠EGA+∠BAD,
从而∠BDA=∠PFA.
因为AF⊥EP,所以∠PFA=90°,于是∠BDA=90°,
故AB是圆的直径.(2)连接BC,DC.由于AB是直径,故∠BDA=∠ACB=90°.
在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,
从而Rt△BDA≌Rt△ACB,于是∠DAB=∠CBA.
又因为∠DCB=∠DAB,所以∠DCB=∠CBA,故DC∥AB.因为AB⊥EP,所以DC⊥EP,∠DCE为直角,于是ED为直径.
由于AB和ED都是圆的直径,故ED=AB.专题一专题二专题一专题二变式训练4?
如图,点A为圆外一点,过点A作圆的两条切线,切点分别为B,C,ADE是圆的割线,连接CD,BD,BE,CE.
(1)求证:BE·CD=BD·CE;
(2)延长CD交AB于点F,若CE∥AB,证明:F为线段AB的中点.专题一专题二考点1考点2考点3考点4考点1:圆周角问题
1.
(2016·全国丙高考)如图,☉O中 的中点为P,弦PC,PD分别交AB于E,F两点.
(1)若∠PFB=2∠PCD,求∠PCD的大小;
(2)若EC的垂直平分线与FD的垂直平分线交于点G,证明OG⊥CD.考点1考点2考点3考点4解(1)连接PB,BC,
则∠BFD=∠PBA+∠BPD,∠PCD=∠PCB+∠BCD.
所以∠PBA=∠PCB.
又∠BPD=∠BCD,
所以∠BFD=∠PCD.
又∠PFB+∠BFD=180°,∠PFB=2∠PCD,
所以3∠PCD=180°,因此∠PCD=60°.考点1考点2考点3考点4(2)因为∠PCD=∠BFD,所以∠EFD+∠PCD=180°,
由此知C,D,F,E四点共圆,其圆心既在CE的垂直平分线上,又在DF的垂直平分线上,故G就是过C,D,F,E四点的圆的圆心,
所以G在CD的垂直平分线上.
又O也在CD的垂直平分线上,因此OG⊥CD.考点1考点2考点3考点42.(2013·课标全国Ⅰ高考)
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
(1)证明:DB=DC;
(2)设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.考点1考点2考点3考点4(1)证明
连接DE,交BC于点G.
由弦切角定理得,∠ABE=∠BCE.
而∠ABE=∠CBE,故∠CBE=∠BCE,BE=CE.
又因为DB⊥BE,
所以DE为直径,∠DCE=90°,
由勾股定理可得DB=DC.考点1考点2考点3考点4考点2:圆内接四边形问题
3.(2015·湖南高考)如图,在☉O中,相交于点E的两弦AB,CD的中点分别是M,N.直线MO与直线CD相交于点F.证明:
(1)∠MEN+∠NOM=180°;
(2)FE·FN=FM·FO.考点1考点2考点3考点4证明
(1)如图所示,因为M,N分别是弦AB,CD的中点,所以OM⊥AB,ON⊥CD,即∠OME=90°,∠ENO=90°,因此∠OME+∠ENO=180°.
又四边形的内角和等于360°,故∠MEN+∠NOM=180°.
(2)由(1)知,O,M,E,N四点共圆,故由割线定理即得FE·FN=FM·FO.考点1考点2考点3考点44.(2016·全国乙高考)
如图,△OAB是等腰三角形,∠AOB=120°,以O为圆心, OA为半径作圆.
(1)证明:直线AB与☉O相切;
(2)点C,D在☉O上,且A,B,C,D四点共圆,证明:AB∥CD.考点1考点2考点3考点4解(1)设E是AB的中点,连接OE.
因为OA=OB,∠AOB=120°,
所以OE⊥AB,∠AOE=60°.
在Rt△AOE中,OE= AO,即O到直线AB的距离等于☉O半径,所以直线AB与☉O相切.
(2)因为OA=2OD,所以O不是A,B,C,D四点所在圆的圆心.
设O'是A,B,C,D四点所在圆的圆心,作直线OO'.
由已知得O在线段AB的垂直平分线上,
又O'在线段AB的垂直平分线上,所以OO'⊥AB.
同理可证,OO'⊥CD.所以AB∥CD.考点1考点2考点3考点4考点3:切割线问题
5.(2016·天津高考)如图,AB是圆的直径,弦CD与AB相交于点E,BE=2AE=2,BD=ED,则线段CE的长为 .?考点1考点2考点3考点4考点1考点2考点3考点46.(2015·重庆高考)如图,圆O的弦AB,CD相交于
点E,过点A作圆O的切线与DC的延长线交于
点P,若PA=6,AE=9,PC=3,CE∶ED=2∶1,
则BE= .?
解析因为PA是圆的切线,所以有PA2=PC·PD,
因此CD=PD-PC=9.
又因为CE∶ED=2∶1,所以CE=6,ED=3.
又由相交弦定理可得AE·BE=CE·ED,
答案2考点1考点2考点3考点4考点1考点2考点3考点4考点4:切线问题
8.(2015·广东高考)如图,已知AB是圆O的直径,AB=4,EC是圆O的切线,切点为C,BC=1,过圆心O作BC的平行线,分别交EC和AC于点D和点P,则OD= .?考点1考点2考点3考点4考点1考点2考点3考点49.(2013·重庆高考)如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则DE的长为 .?
解析在Rt△ABC中,∠A=60°,AB=20,可得BC=10
由弦切角定理,可得∠BCD=∠A=60°.
在Rt△BCD中,可求得CD=5 ,BD=15.
又由切割线定理,可得CD2=DE·DB,可求得DE=5.
答案5考点1考点2考点3考点410.(2015·课标全国Ⅰ高考)
如图,AB是☉O的直径,AC是☉O的切线,BC交☉O于点E.
(1)若D为AC的中点,证明:DE是☉O的切线;
(2)若OA= CE,求∠ACB的大小.考点1考点2考点3考点4解(1)连接AE,由已知得,AE⊥BC,AC⊥AB.
在Rt△AEC中,由已知得,DE=DC,
故∠DEC=∠DCE.
连接OE,则∠OBE=∠OEB.
又∠ACB+∠ABC=90°,
所以∠DEC+∠OEB=90°,
故∠OED=90°,DE是☉O的切线.
