高中数学人教A版选修4-4课件:1.2 极坐标系 :32张PPT
文档属性
| 名称 | 高中数学人教A版选修4-4课件:1.2 极坐标系 :32张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 00:00:00 | ||
图片预览










文档简介
课件32张PPT。二 极坐标系1.极坐标系的概念
(1)极坐标系的建立:在平面内取一个定点O,叫做极点;自极点O引一条射线Ox,叫做极轴;再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.
(2)极坐标系内一点的极坐标的表示:设M是平面内一点,极点O与点M的距离|OM|叫做点M的极径,记为 ρ ;以极轴Ox为始边,射线OM为终边的角xOM叫做点M的极角,记为θ.有序数对(ρ,θ)叫做点M的极坐标,记为M(ρ,θ).?
一般地,不作特殊说明时,我们认为ρ≥0,θ可取任意实数.名师点拨极坐标系的四要素:(1)极点;(2)极轴;(3)长度单位;(4)角度单位和它的正方向.四者缺一不可,其中极轴是以极点为端点的一条射线,它与极轴所在的直线是有区别的;极角θ的始边是极轴,它的终边随着θ的大小和正负而位于不同位置;θ的正方向通常取逆时针方向,θ的值一般是以弧度为单位的量数;点M的极径ρ表示点M与极点O的距离|OM|,因此ρ≥0.2.点的极坐标
一般地,极坐标(ρ,θ)与(ρ,θ+2kπ)(k∈Z)表示同一个点.特别地,极点O的坐标为(0,θ)(θ∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示.
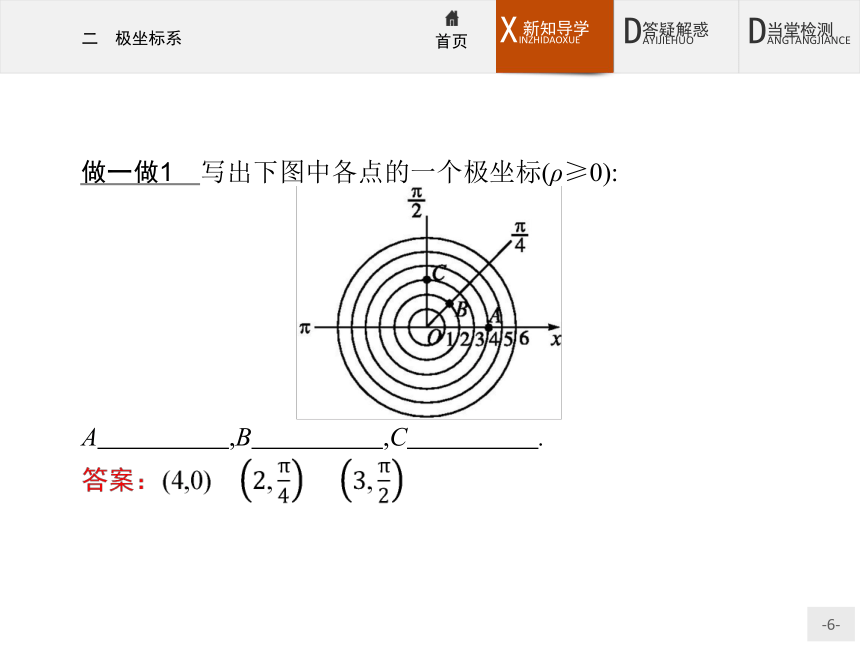
如果规定ρ>0,0≤θ<2π,那么除极点外,平面内的点可用唯一的极坐标(ρ,θ)表示;同时,极坐标(ρ,θ)表示的点也是唯一确定的.做一做1 写出下图中各点的一个极坐标(ρ≥0):?
A ,B ,C .?3.极坐标与直角坐标的互化
(1)互化的前提条件:①极坐标系中的极点与平面直角坐标系中的原点重合;②极轴与x轴的正半轴重合;③两种坐标系取相同的长度单位.
(2)互化公式:名师点拨将直角坐标化为极坐标时,确定ρ和θ的值的方法 做一做2 (1)若点P的直角坐标为(- ),则它的极坐标可表示为( )?(2)已知点M的极坐标为 ,则它的直角坐标为 .?思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)任意一个点都有唯一的极坐标. ( )
(2)若ρ1=ρ2,θ1+θ2=π,则点M1(ρ1,θ1)与点M2(ρ2,θ2)关于极点对称. ( )
(4)当极角θ的取值范围是[0,2π)时,平面上的点(除去极点)与极坐标(ρ,θ)是一一对应关系的. ( )
(5)极坐标与直角坐标在任意情况下均可互化. ( )× × × √ × 探究一探究二思维辨析极坐标的概念?
【例1】 (1)在极坐标系中,作出以下各点:(2)设点A ,直线l为过极点且垂直于极轴的直线,分别求点A关于极轴、直线l、极点的对称点的极坐标(限定ρ>0,0<θ≤2π).
分析:(1)建立极坐标系 作出极角的终边 以极点O为圆心,以极径为半径分别画弧→点的位置;(2)先确定每个点对应的ρ和θ的值,再写出坐标.探究一探究二思维辨析解:(1)A,B,C,D四个点的位置如图所示. 探究一探究二思维辨析探究一探究二思维辨析反思感悟1.由极坐标确定点的位置的步骤:
(1)取定极点O;
(2)作方向为水平向右的射线Ox为极轴;
(3)以极点O为顶点,以极轴Ox为始边,通常按逆时针方向旋转极轴Ox确定出极角的终边;
(4)以极点O为圆心,以极径为半径画弧,弧与极角终边的交点即是所求点的位置.
2.在极坐标系中,点(ρ,θ)关于极轴所在直线对称的点的极坐标为(ρ,2kπ-θ)(k∈Z);关于过极点且垂直于极轴的直线对称的点的极坐标为(ρ,2kπ+π-θ)(k∈Z);关于极点对称的点的极坐标为(ρ,θ+π+2kπ)(k∈Z).探究一探究二思维辨析变式训练1 (1)在极坐标系中,若 ,则点A关于射线OP的对称点的极坐标为 (限定ρ>0,0≤θ<2π);?
(2)写出下图中除极点外各点的极坐标(ρ>0,0≤θ<2π,且各线之间间距相等).探究一探究二思维辨析探究一探究二思维辨析极坐标与直角坐标的互化? 分析:直接利用直角坐标与极坐标的互化公式即可. 探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析反思感悟1.将点的极坐标(ρ,θ)化为直角坐标(x,y)时,需要求角θ的余弦值和正弦值,因此应熟练掌握特殊角的三角函数值,灵活运用三角恒等变换公式进行求解.2.将点的直角坐标(x,y)化为极坐标(ρ,θ)时,只需运用公式 时,要根据直角坐标的符号特征判断出点所在的象限.如果允许θ∈R,那么再根据终边相同的角的意义,表示为θ+2kπ(k∈Z)即可.探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析对点的极坐标理解不清致误
典例已知点A的极坐标是 ,则使ρ>0,-2π≤θ<0的极坐标是什么?使ρ>0,-10π≤θ<-6π的极坐标是什么?探究一探究二思维辨析探究一探究二思维辨析纠错心得在极坐标系中,同一个点的极坐标可以有多种表示形式,它们之间可以相互转化,但要注意互化规则.本题中由于对各种表示形式的等价性理解不清,导致错误.探究一探究二思维辨析变式训练 在极坐标系中,下列各点中与 不表示同一个点的是( )?答案:C 1 2 3 4 51.与点P(ρ,θ)表示同一个点的是( )
A.(ρ,π+θ) B.(ρ,π-θ)
C.(ρ,2kπ+θ)(k∈Z) D.(ρ,(2k+1)π+θ)(k∈Z)
答案:C1 2 3 4 52.将点的极坐标(π,-2π)化为直角坐标为( )
A.(π,0) B.(π,2π)
C.(-π,0) D.(-2π,0)
解析:x=πcos(-2π)=π,y=πsin(-2π)=0,所以极坐标(π,-2π)化为直角坐标为(π,0).
答案:A1 2 3 4 53.在极坐标系中,与点 关于极点对称的点的一个坐标是( )解析:点(ρ,θ)关于极点对称的点为(ρ,π+θ+2kπ)(k∈Z),
答案:A1 2 3 4 54.关于极坐标系的下列叙述:
①极轴是一条射线;
②极点的极坐标是(0,0);
③点(0,0)表示极点;
⑤动点M(5,θ)(θ∈R)的轨迹是以极点为圆心,以5为半径的圆.
其中,正确的序号是 .?1 2 3 4 5解析:设极点为O,极轴就是射线Ox,①正确;极点O的极径ρ=0,极角θ是任意实数,极点的极坐标应为(0,θ)(θ∈R),②错误;给定极坐标(0,0),可以在极坐标平面内确定唯一的一点,即极点,③正确;点M与点N的极角分别是 ,二者的终边互为反向延长线,④错误;由于动点M(5,θ)(θ∈R)的极径ρ=5,极角是任意角,故点M的轨迹是以极点O为圆心,5为半径的圆,⑤正确.
答案:①③⑤1 2 3 4 55.将(1)中的极坐标化为直角坐标,将(2)中的直角坐标化为极坐标(ρ>0,0≤θ<2π).
(1)(2,π);(2)(-1,1).
解:(1)x=ρcos θ=2cos π=-2,y=ρsin θ=2sin π=0,
所以点(2,π)所对应的直角坐标为(-2,0).
(1)极坐标系的建立:在平面内取一个定点O,叫做极点;自极点O引一条射线Ox,叫做极轴;再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.
(2)极坐标系内一点的极坐标的表示:设M是平面内一点,极点O与点M的距离|OM|叫做点M的极径,记为 ρ ;以极轴Ox为始边,射线OM为终边的角xOM叫做点M的极角,记为θ.有序数对(ρ,θ)叫做点M的极坐标,记为M(ρ,θ).?
一般地,不作特殊说明时,我们认为ρ≥0,θ可取任意实数.名师点拨极坐标系的四要素:(1)极点;(2)极轴;(3)长度单位;(4)角度单位和它的正方向.四者缺一不可,其中极轴是以极点为端点的一条射线,它与极轴所在的直线是有区别的;极角θ的始边是极轴,它的终边随着θ的大小和正负而位于不同位置;θ的正方向通常取逆时针方向,θ的值一般是以弧度为单位的量数;点M的极径ρ表示点M与极点O的距离|OM|,因此ρ≥0.2.点的极坐标
一般地,极坐标(ρ,θ)与(ρ,θ+2kπ)(k∈Z)表示同一个点.特别地,极点O的坐标为(0,θ)(θ∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示.
如果规定ρ>0,0≤θ<2π,那么除极点外,平面内的点可用唯一的极坐标(ρ,θ)表示;同时,极坐标(ρ,θ)表示的点也是唯一确定的.做一做1 写出下图中各点的一个极坐标(ρ≥0):?
A ,B ,C .?3.极坐标与直角坐标的互化
(1)互化的前提条件:①极坐标系中的极点与平面直角坐标系中的原点重合;②极轴与x轴的正半轴重合;③两种坐标系取相同的长度单位.
(2)互化公式:名师点拨将直角坐标化为极坐标时,确定ρ和θ的值的方法 做一做2 (1)若点P的直角坐标为(- ),则它的极坐标可表示为( )?(2)已知点M的极坐标为 ,则它的直角坐标为 .?思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)任意一个点都有唯一的极坐标. ( )
(2)若ρ1=ρ2,θ1+θ2=π,则点M1(ρ1,θ1)与点M2(ρ2,θ2)关于极点对称. ( )
(4)当极角θ的取值范围是[0,2π)时,平面上的点(除去极点)与极坐标(ρ,θ)是一一对应关系的. ( )
(5)极坐标与直角坐标在任意情况下均可互化. ( )× × × √ × 探究一探究二思维辨析极坐标的概念?
【例1】 (1)在极坐标系中,作出以下各点:(2)设点A ,直线l为过极点且垂直于极轴的直线,分别求点A关于极轴、直线l、极点的对称点的极坐标(限定ρ>0,0<θ≤2π).
分析:(1)建立极坐标系 作出极角的终边 以极点O为圆心,以极径为半径分别画弧→点的位置;(2)先确定每个点对应的ρ和θ的值,再写出坐标.探究一探究二思维辨析解:(1)A,B,C,D四个点的位置如图所示. 探究一探究二思维辨析探究一探究二思维辨析反思感悟1.由极坐标确定点的位置的步骤:
(1)取定极点O;
(2)作方向为水平向右的射线Ox为极轴;
(3)以极点O为顶点,以极轴Ox为始边,通常按逆时针方向旋转极轴Ox确定出极角的终边;
(4)以极点O为圆心,以极径为半径画弧,弧与极角终边的交点即是所求点的位置.
2.在极坐标系中,点(ρ,θ)关于极轴所在直线对称的点的极坐标为(ρ,2kπ-θ)(k∈Z);关于过极点且垂直于极轴的直线对称的点的极坐标为(ρ,2kπ+π-θ)(k∈Z);关于极点对称的点的极坐标为(ρ,θ+π+2kπ)(k∈Z).探究一探究二思维辨析变式训练1 (1)在极坐标系中,若 ,则点A关于射线OP的对称点的极坐标为 (限定ρ>0,0≤θ<2π);?
(2)写出下图中除极点外各点的极坐标(ρ>0,0≤θ<2π,且各线之间间距相等).探究一探究二思维辨析探究一探究二思维辨析极坐标与直角坐标的互化? 分析:直接利用直角坐标与极坐标的互化公式即可. 探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析反思感悟1.将点的极坐标(ρ,θ)化为直角坐标(x,y)时,需要求角θ的余弦值和正弦值,因此应熟练掌握特殊角的三角函数值,灵活运用三角恒等变换公式进行求解.2.将点的直角坐标(x,y)化为极坐标(ρ,θ)时,只需运用公式 时,要根据直角坐标的符号特征判断出点所在的象限.如果允许θ∈R,那么再根据终边相同的角的意义,表示为θ+2kπ(k∈Z)即可.探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析对点的极坐标理解不清致误
典例已知点A的极坐标是 ,则使ρ>0,-2π≤θ<0的极坐标是什么?使ρ>0,-10π≤θ<-6π的极坐标是什么?探究一探究二思维辨析探究一探究二思维辨析纠错心得在极坐标系中,同一个点的极坐标可以有多种表示形式,它们之间可以相互转化,但要注意互化规则.本题中由于对各种表示形式的等价性理解不清,导致错误.探究一探究二思维辨析变式训练 在极坐标系中,下列各点中与 不表示同一个点的是( )?答案:C 1 2 3 4 51.与点P(ρ,θ)表示同一个点的是( )
A.(ρ,π+θ) B.(ρ,π-θ)
C.(ρ,2kπ+θ)(k∈Z) D.(ρ,(2k+1)π+θ)(k∈Z)
答案:C1 2 3 4 52.将点的极坐标(π,-2π)化为直角坐标为( )
A.(π,0) B.(π,2π)
C.(-π,0) D.(-2π,0)
解析:x=πcos(-2π)=π,y=πsin(-2π)=0,所以极坐标(π,-2π)化为直角坐标为(π,0).
答案:A1 2 3 4 53.在极坐标系中,与点 关于极点对称的点的一个坐标是( )解析:点(ρ,θ)关于极点对称的点为(ρ,π+θ+2kπ)(k∈Z),
答案:A1 2 3 4 54.关于极坐标系的下列叙述:
①极轴是一条射线;
②极点的极坐标是(0,0);
③点(0,0)表示极点;
⑤动点M(5,θ)(θ∈R)的轨迹是以极点为圆心,以5为半径的圆.
其中,正确的序号是 .?1 2 3 4 5解析:设极点为O,极轴就是射线Ox,①正确;极点O的极径ρ=0,极角θ是任意实数,极点的极坐标应为(0,θ)(θ∈R),②错误;给定极坐标(0,0),可以在极坐标平面内确定唯一的一点,即极点,③正确;点M与点N的极角分别是 ,二者的终边互为反向延长线,④错误;由于动点M(5,θ)(θ∈R)的极径ρ=5,极角是任意角,故点M的轨迹是以极点O为圆心,5为半径的圆,⑤正确.
答案:①③⑤1 2 3 4 55.将(1)中的极坐标化为直角坐标,将(2)中的直角坐标化为极坐标(ρ>0,0≤θ<2π).
(1)(2,π);(2)(-1,1).
解:(1)x=ρcos θ=2cos π=-2,y=ρsin θ=2sin π=0,
所以点(2,π)所对应的直角坐标为(-2,0).
