高中数学北师大版选修4-4课件:第一章 坐标系 本章整合:23张PPT
文档属性
| 名称 | 高中数学北师大版选修4-4课件:第一章 坐标系 本章整合:23张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 860.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 12:30:37 | ||
图片预览








文档简介
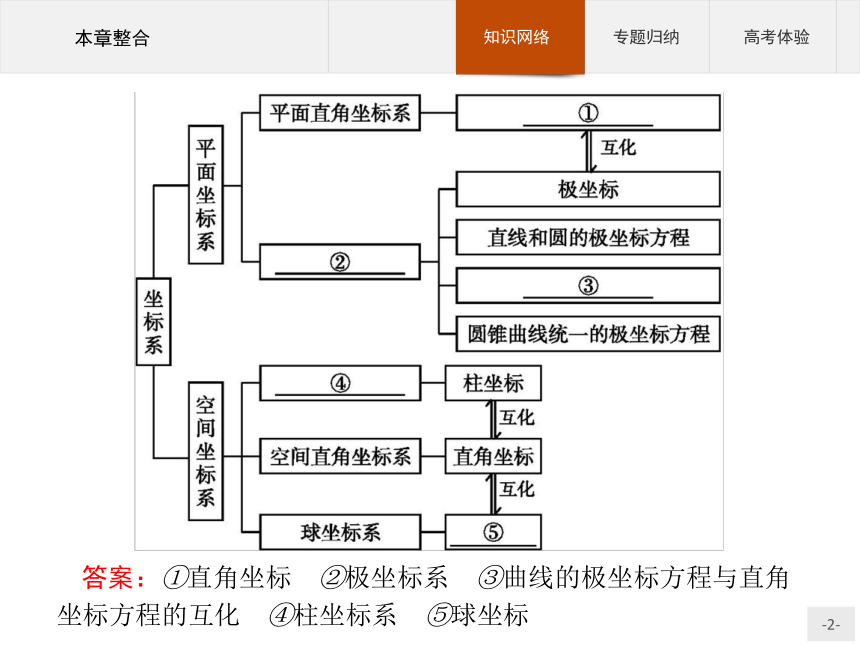
课件23张PPT。本章整合答案:①直角坐标 ②极坐标系 ③曲线的极坐标方程与直角坐标方程的互化 ④柱坐标系 ⑤球坐标专题一专题二专题三专题一 求曲线的极坐标方程
求曲线的极坐标方程的方法和步骤与求直角坐标方程类似,就是把曲线看作适合某种条件的点的集合或轨迹,将已知条件用曲线上点的极坐标ρ,θ的关系式f(ρ,θ)=0表示出来,就得到曲线的极坐标方程.
由于平面上点的极坐标的表示形式不唯一,因此曲线的极坐标方程和直角坐标方程也有不同之处,一条曲线上的点的极坐标有多组表示形式,有些表示形式可能不满足方程,这里要求至少有一组能满足极坐标方程.专题一专题二专题三例1设点P的极坐标为(ρ1,θ1),直线l过点P且与极轴所成的角为α,求直线l的极坐标方程.
分析:先设直线l上任意一点M(ρ,θ),再利用直线在极坐标系中相应的关系列出式子.
解:如图,设点M(ρ,θ)为直线l上除点P外的任意一点,
连接OM,则|OM|=ρ,∠xOM=θ.
由点P的极坐标为(ρ1,θ1),
知|OP|=ρ1,∠xOP=θ1.
设直线l与极轴交于点A,已知直线l与极轴成α角.
于是∠xAM=α.
在△MOP中,∠OMP=α-θ,∠OPM=π-(α-θ1),专题一专题二专题三变式训练1在直角坐标系xOy中,以点O为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为ρcos =1,点M,N分别为曲线C与x轴、y轴的交点.
(1)写出曲线C的直角坐标方程,并求点M,N的极坐标;
(2)设MN的中点为点P,求直线OP的极坐标方程.专题一专题二专题三专题一专题二专题三专题一专题二专题三专题二 极坐标与直角坐标互化
互化的前提依旧是把直角坐标系的原点作为极点,x轴的正半轴作为极轴并在两种坐标系下取相同的单位.
互化公式为x=ρcos θ,y=ρsin θ
ρ2=x2+y2
直角坐标方程化极坐标方程可直接将x=ρcos θ,y=ρsin θ代入即可,而极坐标方程化为直角坐标方程通常先将极坐标方程化为ρcos θ,ρsin θ的整体形式,然后用x,y代替较为方便,常常两端同乘ρ即可达到目的,但要注意变形的等价性.专题一专题二专题三例2已知极坐标方程C1为ρ=10,C2为ρsin =6.
(1)化C1,C2的极坐标方程为直角坐标方程,并分别判断曲线形状;
(2)求C1,C2交点间的距离.解:(1)由ρ=10,得ρ2=100,即x2+y2=100,
故C1为圆心在(0,0),半径等于10的圆.专题一专题二专题三专题一专题二专题三变式训练2 化圆的直角坐标方程x2+y2-2ax=0(a≠0)为极坐标方程.?
解:将x=ρcos θ,y=ρsin θ代入x2+y2-2ax=0,
得ρ2cos2θ+ρ2sin2θ-2aρcos θ=0,
即ρ=2acos θ(a≠0).
所以所求极坐标方程为ρ=2acos θ(a≠0).专题一专题二专题三专题三 极坐标方程及其应用
借助点的极坐标或曲线的极坐标方程,将最值问题转化为三角函数问题求解.专题一专题二专题三例3在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C1的极坐标方程为(1)写出曲线C1与直线l的直角坐标方程;
(2)设Q为曲线C1上一动点,求点Q到直线l距离的最小值.解:(1)根据ρ2=x2+y2,x=ρcos θ,y=ρsin θ,
得曲线C1的直角坐标方程为x2+2y2=2,专题一专题二专题三变式训练3 在极坐标系中,曲线C:ρ=2acos θ(a>0),直线l:
,曲线C与直线l有且仅有一个公共点.
(1)求a;
(2)O为极点,A,B为曲线C上的两点,且∠AOB= ,求|OA|+|OB|的最大值.解:(1)曲线C:ρ=2acos θ(a>0),可变形为ρ2=2ρacos θ,
化为x2+y2=2ax,即(x-a)2+y2=a2.
所以曲线C是以(a,0)为圆心,以a为半径的圆.专题一专题二专题三1234567考点一:极坐标与直角坐标的互化
1.(2014广东高考)在极坐标系中,曲线C1与C2的方程分别为2ρcos2θ=sin θ与ρcos θ=1.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,则曲线C1与C2交点的直角坐标为 .?解析:曲线C1的直角坐标方程为y=2x2,曲线C2的直角坐标方程为
x=1,联立 因此交点的直角坐标为(1,2).
答案:(1,2)12345672.(2014陕西高考)在极坐标系中,点 的距离是 .?答案:1 1234567考点二:极坐标方程及应用
3.(2016北京高考)在极坐标系中,直线ρcos θ- ρsin θ-1=0与圆ρ=2cos θ交于A,B两点,则|AB|= .?答案:2 12345674.(2014天津高考)在以O为极点的极坐标系中,圆ρ=4sin θ和直线ρsin θ=a相交于A,B两点,若△AOB是等边三角形,则a的值为 .?
解析:由ρ=4sin θ可得ρ2=4ρsin θ,所以x2+y2=4y.
所以圆的直角坐标方程为x2+y2=4y,其圆心为C(0,2),半径r=2;
由ρsin θ=a,得直线的直角坐标方程为y=a,由于△AOB是等边三角形,所以圆心C是等边三角形OAB的中心,若设AB的中点为D(如图).
则CD=CB·sin 30°=2× =1,即a-2=1,
所以a=3.
答案:312345675.(2017课标Ⅱ卷高考)在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcos θ=4.
(1)M为曲线C1上的动点,点P在线段OM上,且满足|OM|·|OP|=16,求点P的轨迹C2的直角坐标方程;
(2)设点A的极坐标为 ,点B在曲线C2上,求△OAB面积的最大值.解:(1)设点P的极坐标为(ρ,θ)(ρ>0),点M的极坐标为(ρ1,θ)(ρ1>0).由|OM|·|OP|=16得C2的极坐标方程ρ=4cos θ(ρ>0).
因此C2的直角坐标方程为(x-2)2+y2=4(x≠0).1234567(2)设点B的极坐标为(ρB,α)(ρB>0).
由题设知|OA|=2,ρB=4cos α,于是△OAB面积12345676.(2015江苏高考)已知圆C的极坐标方程为 -4=0,求圆C的半径.解:以极坐标系的极点为平面直角坐标系的原点O,以极轴为x轴的正半轴,建立直角坐标系xOy.
化简,得ρ2+2ρsin θ-2ρcos θ-4=0.
则圆C的直角坐标方程为x2+y2-2x+2y-4=0,
即(x-1)2+(y+1)2=6,
所以圆C的半径为12345677.(2015课标Ⅰ卷高考)在直角坐标系xOy中,直线C1:x=-2,圆C2:(x-1)2+(y-2)2=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.
(1)求C1,C2的极坐标方程;
(2)若直线C3的极坐标方程为θ= (ρ∈R),设C2与C3的交点为M,N,求△C2MN的面积.解:(1)因为x=ρcos θ,y=ρsin θ,
所以C1的极坐标方程为ρcos θ=-2,C2的极坐标方程为ρ2-2ρcos θ-4ρsin θ+4=0.
求曲线的极坐标方程的方法和步骤与求直角坐标方程类似,就是把曲线看作适合某种条件的点的集合或轨迹,将已知条件用曲线上点的极坐标ρ,θ的关系式f(ρ,θ)=0表示出来,就得到曲线的极坐标方程.
由于平面上点的极坐标的表示形式不唯一,因此曲线的极坐标方程和直角坐标方程也有不同之处,一条曲线上的点的极坐标有多组表示形式,有些表示形式可能不满足方程,这里要求至少有一组能满足极坐标方程.专题一专题二专题三例1设点P的极坐标为(ρ1,θ1),直线l过点P且与极轴所成的角为α,求直线l的极坐标方程.
分析:先设直线l上任意一点M(ρ,θ),再利用直线在极坐标系中相应的关系列出式子.
解:如图,设点M(ρ,θ)为直线l上除点P外的任意一点,
连接OM,则|OM|=ρ,∠xOM=θ.
由点P的极坐标为(ρ1,θ1),
知|OP|=ρ1,∠xOP=θ1.
设直线l与极轴交于点A,已知直线l与极轴成α角.
于是∠xAM=α.
在△MOP中,∠OMP=α-θ,∠OPM=π-(α-θ1),专题一专题二专题三变式训练1在直角坐标系xOy中,以点O为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为ρcos =1,点M,N分别为曲线C与x轴、y轴的交点.
(1)写出曲线C的直角坐标方程,并求点M,N的极坐标;
(2)设MN的中点为点P,求直线OP的极坐标方程.专题一专题二专题三专题一专题二专题三专题一专题二专题三专题二 极坐标与直角坐标互化
互化的前提依旧是把直角坐标系的原点作为极点,x轴的正半轴作为极轴并在两种坐标系下取相同的单位.
互化公式为x=ρcos θ,y=ρsin θ
ρ2=x2+y2
直角坐标方程化极坐标方程可直接将x=ρcos θ,y=ρsin θ代入即可,而极坐标方程化为直角坐标方程通常先将极坐标方程化为ρcos θ,ρsin θ的整体形式,然后用x,y代替较为方便,常常两端同乘ρ即可达到目的,但要注意变形的等价性.专题一专题二专题三例2已知极坐标方程C1为ρ=10,C2为ρsin =6.
(1)化C1,C2的极坐标方程为直角坐标方程,并分别判断曲线形状;
(2)求C1,C2交点间的距离.解:(1)由ρ=10,得ρ2=100,即x2+y2=100,
故C1为圆心在(0,0),半径等于10的圆.专题一专题二专题三专题一专题二专题三变式训练2 化圆的直角坐标方程x2+y2-2ax=0(a≠0)为极坐标方程.?
解:将x=ρcos θ,y=ρsin θ代入x2+y2-2ax=0,
得ρ2cos2θ+ρ2sin2θ-2aρcos θ=0,
即ρ=2acos θ(a≠0).
所以所求极坐标方程为ρ=2acos θ(a≠0).专题一专题二专题三专题三 极坐标方程及其应用
借助点的极坐标或曲线的极坐标方程,将最值问题转化为三角函数问题求解.专题一专题二专题三例3在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C1的极坐标方程为(1)写出曲线C1与直线l的直角坐标方程;
(2)设Q为曲线C1上一动点,求点Q到直线l距离的最小值.解:(1)根据ρ2=x2+y2,x=ρcos θ,y=ρsin θ,
得曲线C1的直角坐标方程为x2+2y2=2,专题一专题二专题三变式训练3 在极坐标系中,曲线C:ρ=2acos θ(a>0),直线l:
,曲线C与直线l有且仅有一个公共点.
(1)求a;
(2)O为极点,A,B为曲线C上的两点,且∠AOB= ,求|OA|+|OB|的最大值.解:(1)曲线C:ρ=2acos θ(a>0),可变形为ρ2=2ρacos θ,
化为x2+y2=2ax,即(x-a)2+y2=a2.
所以曲线C是以(a,0)为圆心,以a为半径的圆.专题一专题二专题三1234567考点一:极坐标与直角坐标的互化
1.(2014广东高考)在极坐标系中,曲线C1与C2的方程分别为2ρcos2θ=sin θ与ρcos θ=1.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,则曲线C1与C2交点的直角坐标为 .?解析:曲线C1的直角坐标方程为y=2x2,曲线C2的直角坐标方程为
x=1,联立 因此交点的直角坐标为(1,2).
答案:(1,2)12345672.(2014陕西高考)在极坐标系中,点 的距离是 .?答案:1 1234567考点二:极坐标方程及应用
3.(2016北京高考)在极坐标系中,直线ρcos θ- ρsin θ-1=0与圆ρ=2cos θ交于A,B两点,则|AB|= .?答案:2 12345674.(2014天津高考)在以O为极点的极坐标系中,圆ρ=4sin θ和直线ρsin θ=a相交于A,B两点,若△AOB是等边三角形,则a的值为 .?
解析:由ρ=4sin θ可得ρ2=4ρsin θ,所以x2+y2=4y.
所以圆的直角坐标方程为x2+y2=4y,其圆心为C(0,2),半径r=2;
由ρsin θ=a,得直线的直角坐标方程为y=a,由于△AOB是等边三角形,所以圆心C是等边三角形OAB的中心,若设AB的中点为D(如图).
则CD=CB·sin 30°=2× =1,即a-2=1,
所以a=3.
答案:312345675.(2017课标Ⅱ卷高考)在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcos θ=4.
(1)M为曲线C1上的动点,点P在线段OM上,且满足|OM|·|OP|=16,求点P的轨迹C2的直角坐标方程;
(2)设点A的极坐标为 ,点B在曲线C2上,求△OAB面积的最大值.解:(1)设点P的极坐标为(ρ,θ)(ρ>0),点M的极坐标为(ρ1,θ)(ρ1>0).由|OM|·|OP|=16得C2的极坐标方程ρ=4cos θ(ρ>0).
因此C2的直角坐标方程为(x-2)2+y2=4(x≠0).1234567(2)设点B的极坐标为(ρB,α)(ρB>0).
由题设知|OA|=2,ρB=4cos α,于是△OAB面积12345676.(2015江苏高考)已知圆C的极坐标方程为 -4=0,求圆C的半径.解:以极坐标系的极点为平面直角坐标系的原点O,以极轴为x轴的正半轴,建立直角坐标系xOy.
化简,得ρ2+2ρsin θ-2ρcos θ-4=0.
则圆C的直角坐标方程为x2+y2-2x+2y-4=0,
即(x-1)2+(y+1)2=6,
所以圆C的半径为12345677.(2015课标Ⅰ卷高考)在直角坐标系xOy中,直线C1:x=-2,圆C2:(x-1)2+(y-2)2=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.
(1)求C1,C2的极坐标方程;
(2)若直线C3的极坐标方程为θ= (ρ∈R),设C2与C3的交点为M,N,求△C2MN的面积.解:(1)因为x=ρcos θ,y=ρsin θ,
所以C1的极坐标方程为ρcos θ=-2,C2的极坐标方程为ρ2-2ρcos θ-4ρsin θ+4=0.
同课章节目录
