苏科版九年级数学上册第2章 对称图形——圆期中复习学案(无答案)
文档属性
| 名称 | 苏科版九年级数学上册第2章 对称图形——圆期中复习学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 63.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-13 16:54:53 | ||
图片预览


文档简介
期中复习(3) 对称图形---圆
授课人: 班级: 姓名: 小组:
【学习目标】 1.熟练掌握圆中的相关概念及一些基本的定理.
会利用定义、定理、结论解决圆中的问题.
【学习重点、难点】圆中的综合应用
自主学习 ----- 我能行
知识要点:
(1)圆的基本性质
1、圆外一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是
2、⊙O的半径为10cm,两平行弦AC,BD的长分别为12cm,16cm,则两弦间的距离__________
3、如图7-25,在△ABC中,∠C是直角,∠A=32O ,以点C为圆心、BC为半径作圆,交AB于点D,交AC于点E,则的度数是______.
(2)与圆的位置关系
4、在锐角△ABC中,∠A=50O ,若点O为外心,则∠BOC=_____;若点I为内心,则∠BIC=_____.
5、直角三角形两直角边分别长3和4,则它的内切圆半径是 ,外接圆半径是
6、如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE .
(1)求证:AE是⊙O的切线;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
(3)与圆的有关计算
7、圆弧的半径为3,弧所对的圆心角为60°,则该弧的长度为 .
8、如果圆锥的高为8cm,母线长为10cm,则它的侧面展开图的面积为 .
9、在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
(1)求证:BE=CE; (2)若BD=1,BE=2,求AC的长.
【自学疑惑】
二、合作探究 ----- 我快乐
1、在Rt△ABC中,∠C=90O,AC=5,AB=13.
(1)以点A为圆心、4为半径的圆A与直线BC的位置关系是_____.
(2) 以点C为圆心,当半径为______时,圆C与直线AB相切.
(3) 以点C为圆心,当半径为 时,圆C与边AB有一个交点.
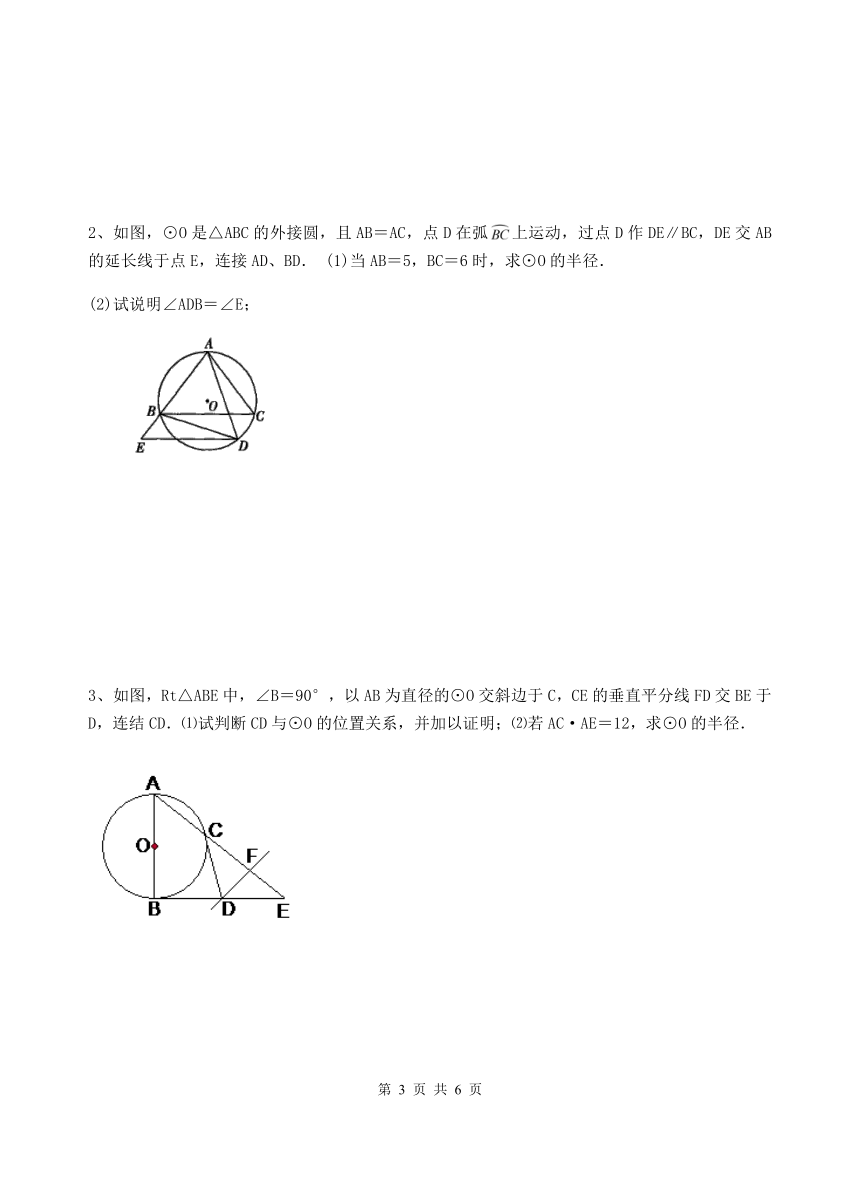
如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧上运动,过点D作DE∥BC,DE交AB的延长线于点E,连接AD、BD. (1)当AB=5,BC=6时,求⊙O的半径.
(2)试说明∠ADB=∠E;
如图,Rt△ABE中,∠B=90°,以AB为直径的⊙O交斜边于C,CE的垂直平分线FD交BE于D,连结CD.⑴试判断CD与⊙O的位置关系,并加以证明;⑵若AC·AE=12,求⊙O的半径.?
?????????
三、自主反思 ---- 我成长
通过这节课的学习,学到了什么新知识?有何感悟?获得了什么经验?
四、教学反思:
课后巩固----- 我自觉
1.三角形的外心是( )
A.三条中线的交点 B.三条边的中垂线的交点 C.三条高的交点 D.三条角平分线的交点
2、下列四个命题:①直径所对的圆周角是直角;②圆既是轴对称图形,又是中心对称图形;③在同圆中,相等的圆周角所对的弦相等;④三点确定一个圆.其中正确命题的个数为( )
A.1 B. 2 C.3 D. 4
3、一个形式如圆锥的冰淇淋纸筒,其底面直径为,母线长为,围成这样的冰淇淋纸筒所需纸片的面积是 ( )
A. B. C. D.
4、一个顶点周围有边长相同的m个正三角形和n个正方形组合能够密铺地面,则m+n=
6、一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是 .
7、正八边形的每一个内角是 °,绕着它的中心至少旋转 °和自身重合。
正三角形的半径为r,它的边长是 ,正四边形的半径为r,它的边长是
8、AB切⊙O于点B,AC交⊙O于点M?、N,若四边形OABN恰为平行四边形,且弦BN的长为10cm.
(1)求⊙O的半径长及图中阴影部分的面积S.?
(2)求MN的长.?
9、如图,在Rt⊿ABC中,∠ACB=90°,以斜边AB上一点O为圆心,
OB为半径作⊙O,交AC于点E,交AB于点D,且∠BEC=∠BDE.
(1)求证:AC是⊙O的切线;
(2)连接OC交BE于点F,若,求的值.
六、展示提升 ---- 我最棒
1、如图,△ABC是等边三角形,曲线CDEF叫做等边三角形
的渐开线,其中弧CD,弧DE,弧EF的圆心依次是A,B,C,
如果AB=1,那么曲线CDEF的总长是___ _____.
2、如图,在平面直角系中,点A、B分别在x轴、y轴上,A(8,0),B(0,6),点P从点B出发,沿BA以每秒1个单位的速度向点A运动,点Q从点A出发,沿AO以每秒1个单位的速度向点O运动,当点Q到达点O时,两点同时停止运动,设点Q的运动时间为t秒.
用含t的代数式表示C点坐标;
如图1,连接PQ,过点Q作QC⊥AO交AB于点C,在整个运动过程中,当t为何值时,△CPQ为等腰三角形?
如图2,以QC为直径作⊙D,⊙D与AB的另一个公共点为E.问是否存在某一时刻t,使得以BC、CE、AE的长为边的三角形为直角三角形?若存在,直接写出一个符合题意的t的值;若不存在,请说明理由.??????
授课人: 班级: 姓名: 小组:
【学习目标】 1.熟练掌握圆中的相关概念及一些基本的定理.
会利用定义、定理、结论解决圆中的问题.
【学习重点、难点】圆中的综合应用
自主学习 ----- 我能行
知识要点:
(1)圆的基本性质
1、圆外一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是
2、⊙O的半径为10cm,两平行弦AC,BD的长分别为12cm,16cm,则两弦间的距离__________
3、如图7-25,在△ABC中,∠C是直角,∠A=32O ,以点C为圆心、BC为半径作圆,交AB于点D,交AC于点E,则的度数是______.
(2)与圆的位置关系
4、在锐角△ABC中,∠A=50O ,若点O为外心,则∠BOC=_____;若点I为内心,则∠BIC=_____.
5、直角三角形两直角边分别长3和4,则它的内切圆半径是 ,外接圆半径是
6、如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE .
(1)求证:AE是⊙O的切线;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
(3)与圆的有关计算
7、圆弧的半径为3,弧所对的圆心角为60°,则该弧的长度为 .
8、如果圆锥的高为8cm,母线长为10cm,则它的侧面展开图的面积为 .
9、在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
(1)求证:BE=CE; (2)若BD=1,BE=2,求AC的长.
【自学疑惑】
二、合作探究 ----- 我快乐
1、在Rt△ABC中,∠C=90O,AC=5,AB=13.
(1)以点A为圆心、4为半径的圆A与直线BC的位置关系是_____.
(2) 以点C为圆心,当半径为______时,圆C与直线AB相切.
(3) 以点C为圆心,当半径为 时,圆C与边AB有一个交点.
如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧上运动,过点D作DE∥BC,DE交AB的延长线于点E,连接AD、BD. (1)当AB=5,BC=6时,求⊙O的半径.
(2)试说明∠ADB=∠E;
如图,Rt△ABE中,∠B=90°,以AB为直径的⊙O交斜边于C,CE的垂直平分线FD交BE于D,连结CD.⑴试判断CD与⊙O的位置关系,并加以证明;⑵若AC·AE=12,求⊙O的半径.?
?????????
三、自主反思 ---- 我成长
通过这节课的学习,学到了什么新知识?有何感悟?获得了什么经验?
四、教学反思:
课后巩固----- 我自觉
1.三角形的外心是( )
A.三条中线的交点 B.三条边的中垂线的交点 C.三条高的交点 D.三条角平分线的交点
2、下列四个命题:①直径所对的圆周角是直角;②圆既是轴对称图形,又是中心对称图形;③在同圆中,相等的圆周角所对的弦相等;④三点确定一个圆.其中正确命题的个数为( )
A.1 B. 2 C.3 D. 4
3、一个形式如圆锥的冰淇淋纸筒,其底面直径为,母线长为,围成这样的冰淇淋纸筒所需纸片的面积是 ( )
A. B. C. D.
4、一个顶点周围有边长相同的m个正三角形和n个正方形组合能够密铺地面,则m+n=
6、一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是 .
7、正八边形的每一个内角是 °,绕着它的中心至少旋转 °和自身重合。
正三角形的半径为r,它的边长是 ,正四边形的半径为r,它的边长是
8、AB切⊙O于点B,AC交⊙O于点M?、N,若四边形OABN恰为平行四边形,且弦BN的长为10cm.
(1)求⊙O的半径长及图中阴影部分的面积S.?
(2)求MN的长.?
9、如图,在Rt⊿ABC中,∠ACB=90°,以斜边AB上一点O为圆心,
OB为半径作⊙O,交AC于点E,交AB于点D,且∠BEC=∠BDE.
(1)求证:AC是⊙O的切线;
(2)连接OC交BE于点F,若,求的值.
六、展示提升 ---- 我最棒
1、如图,△ABC是等边三角形,曲线CDEF叫做等边三角形
的渐开线,其中弧CD,弧DE,弧EF的圆心依次是A,B,C,
如果AB=1,那么曲线CDEF的总长是___ _____.
2、如图,在平面直角系中,点A、B分别在x轴、y轴上,A(8,0),B(0,6),点P从点B出发,沿BA以每秒1个单位的速度向点A运动,点Q从点A出发,沿AO以每秒1个单位的速度向点O运动,当点Q到达点O时,两点同时停止运动,设点Q的运动时间为t秒.
用含t的代数式表示C点坐标;
如图1,连接PQ,过点Q作QC⊥AO交AB于点C,在整个运动过程中,当t为何值时,△CPQ为等腰三角形?
如图2,以QC为直径作⊙D,⊙D与AB的另一个公共点为E.问是否存在某一时刻t,使得以BC、CE、AE的长为边的三角形为直角三角形?若存在,直接写出一个符合题意的t的值;若不存在,请说明理由.??????
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
