高中数学北师大版必修3课件:1.4 数据的数字特征:29张PPT
文档属性
| 名称 | 高中数学北师大版必修3课件:1.4 数据的数字特征:29张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 791.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 00:00:00 | ||
图片预览







文档简介
课件29张PPT。§4 数据的数字特征1.众数、中位数、平均数
众数、中位数、平均数刻画了一组数据的集中趋势.
(1)众数
一组数据中,出现次数最多的数就是众数.若有两个或几个数据出现的次数相等且都最多,则这些数都是这组数据的众数;若一组数据中,每个数据出现的次数都一样,则这组数据没有众数.
(2)中位数
①把一组数据按从小到大(或从大到小)的顺序排成一排,处于中间位置的数称为这组数据的中位数.
②当数据有奇数个时,位于最中间位置的数就是中位数;当数据有偶数个时,位于最中间的两个数的平均数就是中位数.
(3)平均数
一组数据的和与这组数据的个数的商叫作这组数据的平均数,数据x1,x2,…,xn的平均数为【做一做1】 已知一组数据10,30,50,50,60,70,80.其中平均数、中位数和众数的大小关系是( )
A.平均数>中位数>众数
B.平均数<中位数<众数
C.中位数<众数<平均数
D.众数=中位数=平均数
解析:由所给数据可得平均数为50,中位数为50,众数为50,因此众数=中位数=平均数.
答案:D名师点拨众数、中位数、平均数的比较 2.极差、方差、标准差
极差、方差、标准差刻画了一组数据的离散程度.
(1)极差:把一组数据中最大值与最小值的差叫作这组数据的极差.极差对极端值非常敏感,在一定程度上表明了该组数据的分散程度.
(2)方差【做一做2】 从一堆苹果中任取5只,称得它们的质量如下(单位:克):
125 124 121 123 127
则该样本的标准差s= ?(克)(用数字作答).?答案:2 思考辨析
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)平均数能描述数据的平均水平,定量地反映数据的集中趋势. ( )
(2)用样本来估计总体时,一般来说,样本容量越大,这种估计越精确. ( )
(3)若x1,x2,…,xn的方差为s2,则ax1+b,ax2+b,…,axn+b的方差是as2. ( )
答案:(1)√ (2)√ (3)×探究一探究二探究三探究四思维辨析当堂检测平均数、中位数、众数的计算
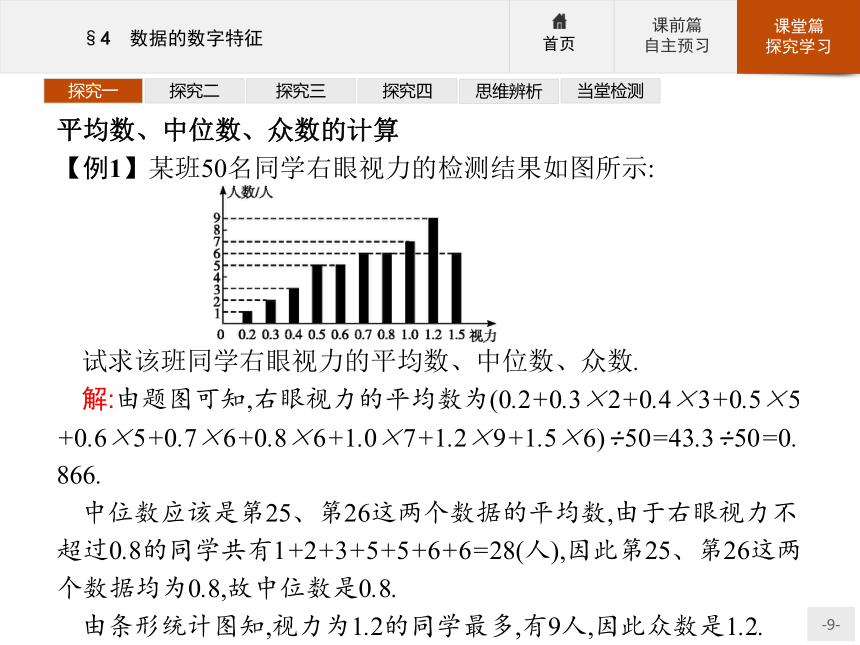
【例1】某班50名同学右眼视力的检测结果如图所示:试求该班同学右眼视力的平均数、中位数、众数.
解:由题图可知,右眼视力的平均数为(0.2+0.3×2+0.4×3+0.5×5 +0.6×5+0.7×6+0.8×6+1.0×7+1.2×9+1.5×6)÷50=43.3÷50=0.866.
中位数应该是第25、第26这两个数据的平均数,由于右眼视力不超过0.8的同学共有1+2+3+5+5+6+6=28(人),因此第25、第26这两个数据均为0.8,故中位数是0.8.
由条形统计图知,视力为1.2的同学最多,有9人,因此众数是1.2.探究一探究二探究三探究四思维辨析当堂检测反思感悟1.通常情况下,给出一组数据后,可根据平均数、中位数、众数的定义及其计算公式分别计算求值.
2.求中位数时,必须先将数据按从大到小或从小到大的顺序排列.
3.当数据是用统计图表的形式给出时,要先通过分析图表,获取数据,再进行计算.探究一探究二探究三探究四思维辨析当堂检测变式训练1以下是某地在甲、乙两个重要道路交叉口设置的电子监控在连续一周时间里抓拍到的每一天的车辆违章次数情况:
甲:6,8,9,10,9,9,12;
乙:7,9,8,11,10,9,11.
试分别求甲、乙两路口车辆违章次数的平均数、中位数、众数.探究一探究二探究三探究四思维辨析当堂检测方差与标准差的计算
【例2】 将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场作的9个分数的茎叶图如图所示,后来有1个数据模糊,无法辨认,在图中以x表示,则7个剩余分数的方差为( )解析:利用平均数为91,求出x的值,利用方差的定义,计算方差.
根据茎叶图,去掉1个最低分87,1个最高分99,答案:B 探究一探究二探究三探究四思维辨析当堂检测反思感悟1.按照定义,求一组数据的方差、标准差的步骤是:
求平均数 →求方差s2→求标准差s
2.如果数据是用统计图表给出的,应先从图表中获取数据信息,再套用公式计算.探究一探究二探究三探究四思维辨析当堂检测变式训练2(1)已知一组数据为-3,5,7,x,11,若这组数据的众数为5,则该组数据的方差为 ;?
(2)已知一组数据的茎叶图如图所示,则该组数据的标准差等于 .(精确到0.01)?探究一探究二探究三探究四思维辨析当堂检测答案:(1)20.8 (2)9.60 探究一探究二探究三探究四思维辨析当堂检测方差与标准差的性质 答案:D 探究一探究二探究三探究四思维辨析当堂检测变式训练3若样本数据x1,x2,…,x10的标准差为8,则数据2x1-1,2x2-1,…,2x10-1的标准差为( )
A.8 B.15 C.16 D.32
答案:C探究一探究二探究三探究四思维辨析当堂检测统计图表与数字特征的综合应用
【例4】甲、乙两位学生参加数学竞赛培训,现分别从他们培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲:82,91,79,78,95,88,83,84
乙:92,95,80,75,83,80,90,85
(1)画出甲、乙两位学生成绩的茎叶图.
(2)现要从中选派一人参加数学竞赛,从统计学角度看,你认为应派哪位学生参加数学竞赛,请说明理由.探究一探究二探究三探究四思维辨析当堂检测解:(1)茎叶图如图所示: 探究一探究二探究三探究四思维辨析当堂检测反思感悟处理统计图表与数字特征问题应注意的方法技巧
1.由图形得到对应的样本数据,计算出平均数、方差(标准差).
2.从图形直观分析样本数据的分布情况,大致判断平均数的范围,并利用方差(标准差)的大小反映数据的波动性大小.此点可称为方差(标准差)的几何意义.探究一探究二探究三探究四思维辨析当堂检测答案:B 探究一探究二探究三探究四思维辨析当堂检测对方差概念理解不透彻而致误
【典例】 为了试验杂交水稻和普通水稻在产量和稳定程度上的区别,随机在两块试验田里分别抽取5穗,其中杂交水稻每穗粒数分别为49,50,51,50,50,而普通水稻每穗粒数分别为48,52,43,57,50,试比较这两种水稻哪种更稳定.探究一探究二探究三探究四思维辨析当堂检测纠错心得本题产生错解的原因是对方差的概念及特征理解不透彻,方差是衡量一组数据波动性大小的一个统计量,并且方差越小,表示波动越小,越稳定.探究一探究二探究三探究四思维辨析当堂检测变式训练下列对一组数据的分析,说法不正确的是( )
A.数据的极差越小,样本数据分布越集中、稳定
B.数据的平均数越小,样本数据分布越集中、稳定
C.数据的标准差越小,样本数据分布越集中、稳定
D.数据的方差越小,样本数据分布越集中、稳定
解析:极差、方差、标准差都可以反映数据的离散程度,而平均数不可以,平均数反映的是数据的平均水平.
答案:B探究一探究二探究三探究四思维辨析当堂检测1.已知一组数据从小到大的排列顺序为-1,0,4,x,6,15,若这组数据的中位数为5,则这组数据的众数为( )
A.5 B.6 C.4 D.5.5
解析:因为中位数为 ,所以x=6,故众数为6.
答案:B答案:C 探究一探究二探究三探究四思维辨析当堂检测3.若甲、乙、丙、丁四人参加奥运会射击项目选拔赛,四人的平均成绩和标准差如下表:则参加奥运会的最佳人选应为( )
A.甲 B.乙 C.丙 D.丁
解析:从平均数来看,乙、丙的平均值最大,从标准差来看,丙的标准差最小,因此,应选择丙参加比赛.
答案:C探究一探究二探究三探究四思维辨析当堂检测4.已知一组数据x1,x2,…,xn的方差是a,则另一组数据x1-2,x2-2,…,xn-2的方差是 .?
解析:将一组数据同时加上或减去一个数,所得新数据的方差与原数据的方差相等.
答案:a探究一探究二探究三探究四思维辨析当堂检测5.某车间20名工人年龄数据如下表: (1)求这20名工人年龄的众数与极差;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)求这20名工人年龄的方差.探究一探究二探究三探究四思维辨析当堂检测 解:(1)这20名工人年龄的众数为30;这20名工人年龄的极差为40-19=21.
?
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图如图所示.
(3)这20名工人年龄的平均数为(19+28×3+29×3+30×5+31×4+32×3+40)÷20=30;
所以这20名工人年龄的方差为
众数、中位数、平均数刻画了一组数据的集中趋势.
(1)众数
一组数据中,出现次数最多的数就是众数.若有两个或几个数据出现的次数相等且都最多,则这些数都是这组数据的众数;若一组数据中,每个数据出现的次数都一样,则这组数据没有众数.
(2)中位数
①把一组数据按从小到大(或从大到小)的顺序排成一排,处于中间位置的数称为这组数据的中位数.
②当数据有奇数个时,位于最中间位置的数就是中位数;当数据有偶数个时,位于最中间的两个数的平均数就是中位数.
(3)平均数
一组数据的和与这组数据的个数的商叫作这组数据的平均数,数据x1,x2,…,xn的平均数为【做一做1】 已知一组数据10,30,50,50,60,70,80.其中平均数、中位数和众数的大小关系是( )
A.平均数>中位数>众数
B.平均数<中位数<众数
C.中位数<众数<平均数
D.众数=中位数=平均数
解析:由所给数据可得平均数为50,中位数为50,众数为50,因此众数=中位数=平均数.
答案:D名师点拨众数、中位数、平均数的比较 2.极差、方差、标准差
极差、方差、标准差刻画了一组数据的离散程度.
(1)极差:把一组数据中最大值与最小值的差叫作这组数据的极差.极差对极端值非常敏感,在一定程度上表明了该组数据的分散程度.
(2)方差【做一做2】 从一堆苹果中任取5只,称得它们的质量如下(单位:克):
125 124 121 123 127
则该样本的标准差s= ?(克)(用数字作答).?答案:2 思考辨析
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)平均数能描述数据的平均水平,定量地反映数据的集中趋势. ( )
(2)用样本来估计总体时,一般来说,样本容量越大,这种估计越精确. ( )
(3)若x1,x2,…,xn的方差为s2,则ax1+b,ax2+b,…,axn+b的方差是as2. ( )
答案:(1)√ (2)√ (3)×探究一探究二探究三探究四思维辨析当堂检测平均数、中位数、众数的计算
【例1】某班50名同学右眼视力的检测结果如图所示:试求该班同学右眼视力的平均数、中位数、众数.
解:由题图可知,右眼视力的平均数为(0.2+0.3×2+0.4×3+0.5×5 +0.6×5+0.7×6+0.8×6+1.0×7+1.2×9+1.5×6)÷50=43.3÷50=0.866.
中位数应该是第25、第26这两个数据的平均数,由于右眼视力不超过0.8的同学共有1+2+3+5+5+6+6=28(人),因此第25、第26这两个数据均为0.8,故中位数是0.8.
由条形统计图知,视力为1.2的同学最多,有9人,因此众数是1.2.探究一探究二探究三探究四思维辨析当堂检测反思感悟1.通常情况下,给出一组数据后,可根据平均数、中位数、众数的定义及其计算公式分别计算求值.
2.求中位数时,必须先将数据按从大到小或从小到大的顺序排列.
3.当数据是用统计图表的形式给出时,要先通过分析图表,获取数据,再进行计算.探究一探究二探究三探究四思维辨析当堂检测变式训练1以下是某地在甲、乙两个重要道路交叉口设置的电子监控在连续一周时间里抓拍到的每一天的车辆违章次数情况:
甲:6,8,9,10,9,9,12;
乙:7,9,8,11,10,9,11.
试分别求甲、乙两路口车辆违章次数的平均数、中位数、众数.探究一探究二探究三探究四思维辨析当堂检测方差与标准差的计算
【例2】 将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场作的9个分数的茎叶图如图所示,后来有1个数据模糊,无法辨认,在图中以x表示,则7个剩余分数的方差为( )解析:利用平均数为91,求出x的值,利用方差的定义,计算方差.
根据茎叶图,去掉1个最低分87,1个最高分99,答案:B 探究一探究二探究三探究四思维辨析当堂检测反思感悟1.按照定义,求一组数据的方差、标准差的步骤是:
求平均数 →求方差s2→求标准差s
2.如果数据是用统计图表给出的,应先从图表中获取数据信息,再套用公式计算.探究一探究二探究三探究四思维辨析当堂检测变式训练2(1)已知一组数据为-3,5,7,x,11,若这组数据的众数为5,则该组数据的方差为 ;?
(2)已知一组数据的茎叶图如图所示,则该组数据的标准差等于 .(精确到0.01)?探究一探究二探究三探究四思维辨析当堂检测答案:(1)20.8 (2)9.60 探究一探究二探究三探究四思维辨析当堂检测方差与标准差的性质 答案:D 探究一探究二探究三探究四思维辨析当堂检测变式训练3若样本数据x1,x2,…,x10的标准差为8,则数据2x1-1,2x2-1,…,2x10-1的标准差为( )
A.8 B.15 C.16 D.32
答案:C探究一探究二探究三探究四思维辨析当堂检测统计图表与数字特征的综合应用
【例4】甲、乙两位学生参加数学竞赛培训,现分别从他们培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲:82,91,79,78,95,88,83,84
乙:92,95,80,75,83,80,90,85
(1)画出甲、乙两位学生成绩的茎叶图.
(2)现要从中选派一人参加数学竞赛,从统计学角度看,你认为应派哪位学生参加数学竞赛,请说明理由.探究一探究二探究三探究四思维辨析当堂检测解:(1)茎叶图如图所示: 探究一探究二探究三探究四思维辨析当堂检测反思感悟处理统计图表与数字特征问题应注意的方法技巧
1.由图形得到对应的样本数据,计算出平均数、方差(标准差).
2.从图形直观分析样本数据的分布情况,大致判断平均数的范围,并利用方差(标准差)的大小反映数据的波动性大小.此点可称为方差(标准差)的几何意义.探究一探究二探究三探究四思维辨析当堂检测答案:B 探究一探究二探究三探究四思维辨析当堂检测对方差概念理解不透彻而致误
【典例】 为了试验杂交水稻和普通水稻在产量和稳定程度上的区别,随机在两块试验田里分别抽取5穗,其中杂交水稻每穗粒数分别为49,50,51,50,50,而普通水稻每穗粒数分别为48,52,43,57,50,试比较这两种水稻哪种更稳定.探究一探究二探究三探究四思维辨析当堂检测纠错心得本题产生错解的原因是对方差的概念及特征理解不透彻,方差是衡量一组数据波动性大小的一个统计量,并且方差越小,表示波动越小,越稳定.探究一探究二探究三探究四思维辨析当堂检测变式训练下列对一组数据的分析,说法不正确的是( )
A.数据的极差越小,样本数据分布越集中、稳定
B.数据的平均数越小,样本数据分布越集中、稳定
C.数据的标准差越小,样本数据分布越集中、稳定
D.数据的方差越小,样本数据分布越集中、稳定
解析:极差、方差、标准差都可以反映数据的离散程度,而平均数不可以,平均数反映的是数据的平均水平.
答案:B探究一探究二探究三探究四思维辨析当堂检测1.已知一组数据从小到大的排列顺序为-1,0,4,x,6,15,若这组数据的中位数为5,则这组数据的众数为( )
A.5 B.6 C.4 D.5.5
解析:因为中位数为 ,所以x=6,故众数为6.
答案:B答案:C 探究一探究二探究三探究四思维辨析当堂检测3.若甲、乙、丙、丁四人参加奥运会射击项目选拔赛,四人的平均成绩和标准差如下表:则参加奥运会的最佳人选应为( )
A.甲 B.乙 C.丙 D.丁
解析:从平均数来看,乙、丙的平均值最大,从标准差来看,丙的标准差最小,因此,应选择丙参加比赛.
答案:C探究一探究二探究三探究四思维辨析当堂检测4.已知一组数据x1,x2,…,xn的方差是a,则另一组数据x1-2,x2-2,…,xn-2的方差是 .?
解析:将一组数据同时加上或减去一个数,所得新数据的方差与原数据的方差相等.
答案:a探究一探究二探究三探究四思维辨析当堂检测5.某车间20名工人年龄数据如下表: (1)求这20名工人年龄的众数与极差;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)求这20名工人年龄的方差.探究一探究二探究三探究四思维辨析当堂检测 解:(1)这20名工人年龄的众数为30;这20名工人年龄的极差为40-19=21.
?
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图如图所示.
(3)这20名工人年龄的平均数为(19+28×3+29×3+30×5+31×4+32×3+40)÷20=30;
所以这20名工人年龄的方差为
