高中数学人教A版选修4-1课件:2.5 与圆有关的比例线段 :36张PPT
文档属性
| 名称 | 高中数学人教A版选修4-1课件:2.5 与圆有关的比例线段 :36张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 00:00:00 | ||
图片预览







文档简介
课件36张PPT。五 与圆有关的比例线段12341.相交弦定理
(1)文字叙述:圆内的两条相交弦,被交点分成的两条线段长的积相等.
(2)图形及符号表示:如图所示,AB,CD是☉O的两条弦,AB,CD相交于点P,则PA·PB=PC·PD.1234123412342.割线定理
(1)文字叙述:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.
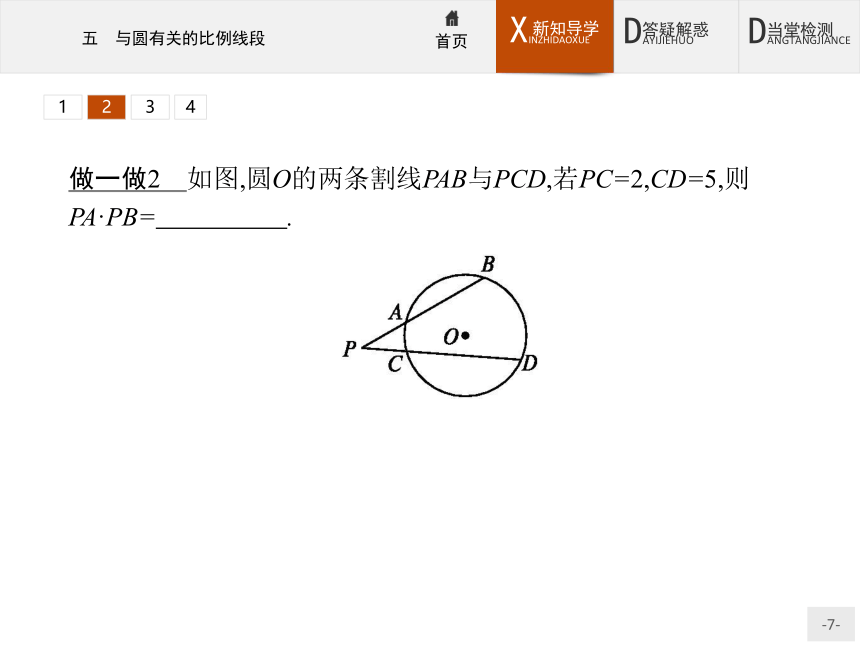
(2)图形及符号表示:如图,PA和PC是圆O的两条割线,与圆分别交于点B,A和D,C,则PA·PB=PC·PD.1234做一做2 如图,圆O的两条割线PAB与PCD,若PC=2,CD=5,则PA·PB= .?
解析由割线定理可得PA·PB=PC·PD,于是PA·PB=2×(2+5)=14.
答案1412343.切割线定理
(1)文字叙述:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.
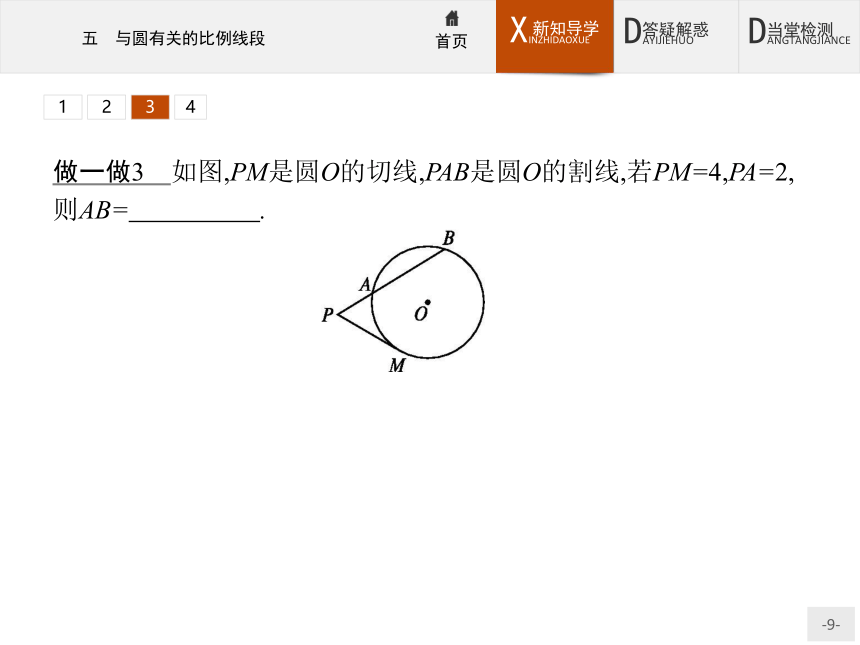
(2)图形及符号表示:如图,从☉O外一点P引圆的切线PA和割线PBC,A是切点,则PA2=PB·PC.1234做一做3 如图,PM是圆O的切线,PAB是圆O的割线,若PM=4,PA=2,则AB= .?解析由切割线定理可得PM2=PA·PB,于是42=2(2+AB),解得AB=6.
答案612344.切线长定理
(1)文字叙述:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
(2)图形及符号表示:如图,PA,PB分别与☉O相切于点A,B,则PA=PB,∠OPA=∠OPB.12341234做一做4?
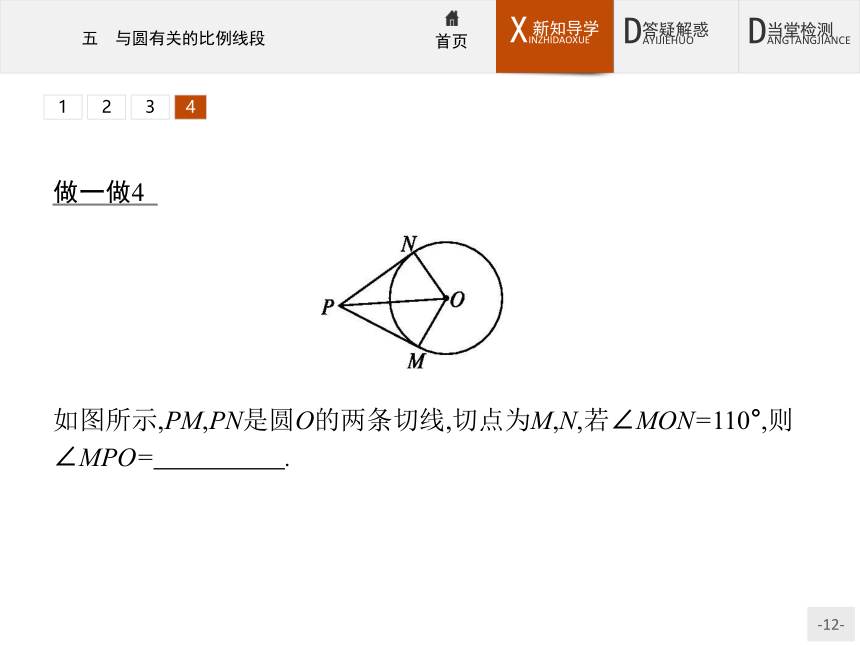
如图所示,PM,PN是圆O的两条切线,切点为M,N,若∠MON=110°,则∠MPO= .?
解析由切线长定理可知PM=PN,∠OPN=∠OPM,而∠MON=110°,所以∠MPN=70°,从而∠MPO=35°.
答案35°1234思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)若圆O的两条割线是PAB与PCD,则有PA·AB=PC·CD. ( )
(2)如果AB,CD是☉O的两条相交弦,交点为P,且AB被点P平分,那么PA是PC与PD的比例中项. ( )
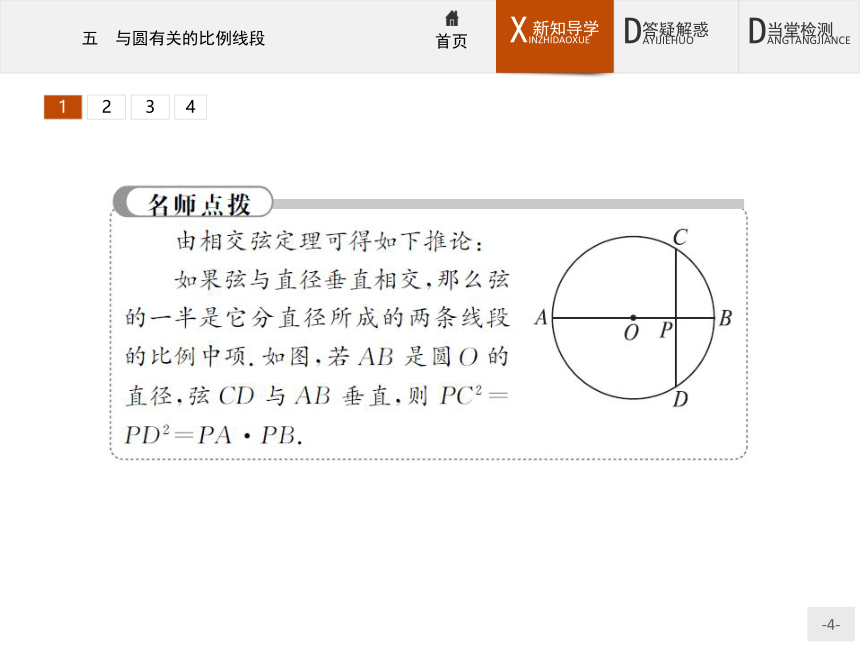
(3)如果圆的一条弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项. ( )
(4)如果PAB,PCD是☉O的两条割线,且PA=PC,那么PB与PD相等. ( )
答案(1)× (2)√ (3)√ (4)√探究一探究二探究三规范解答探究一相交弦定理的应用?
【例1】如图,在圆O中,M,N是弦AB的三等分点,弦CD,CE分别经过点M,N.若CM=2,MD=4,CN=3,则线段NE的长为( )探究一探究二探究三规范解答探究一探究二探究三规范解答变式训练1?
如图,AC为☉O的直径,弦BD⊥AC于点P,PC=2,PA=8,则tan∠ACD的值为 .?
解析∵AC为☉O的直径,弦BD⊥AC,∴PB=PD,∠APB=90°.
由相交弦定理得PB·PD=PA·PC,即PB2=8×2=16,∴PB=4.
答案2探究一探究二探究三规范解答探究二切割线定理的应用?
【例2】
如图,AD为☉O的直径,AB为☉O的切线,割线BMN交AD的延长线于C,且BM=MN=NC,AB=2
求:(1)BC的长;(2)☉O的半径r.
分析对于(1),可由切割线定理求得BM的长,从而求出BC的长度;对于(2),应由割线定理求得半径.探究一探究二探究三规范解答探究一探究二探究三规范解答探究一探究二探究三规范解答变式训练2?
如图,AB切☉O于B,ACD为割线,E为 的中点,BE交DC于F,求证:AF2=AC·AD.
证明连接BC,BD.∵E为 的中点,
∴∠DBE=∠CBE.
又AB是☉O的切线,
∴∠ABC=∠CDB.
∴∠ABC+∠CBE=∠DBE+∠CDB,即∠ABF=∠AFB.∴AB=AF.
又AB是☉O的切线,ACD为割线,由切割线定理可知AC·AD=AB2,
∴AF2=AC·AD.探究一探究二探究三规范解答探究三切线长定理的应用?
【例3】
如图,已知AB是☉O的直径,C为圆上任意一点,过点C的切线分别与过A,B两点的切线交于P,Q.求证:AB2=4AP·BQ.
分析一种思路是证明△AOP∽△BQO,通过对应边成比例结合切线长定理进行证明;另一种思路是在Rt△POQ中,利用射影定理结合切线长定理进行证明.探究一探究二探究三规范解答证明(证法1)
连接OP,OQ,如图.
∵AP,PQ,BQ为☉O的切线,
∴∠1=∠2,∠3=∠4.
∵AP,BQ为☉O的切线,AB为直径,
∴AB⊥AP,AB⊥BQ,
∴AP∥BQ.
∴∠A=∠B=90°,∠1+∠2+∠3+∠4=180°.
∴∠1+∠4=∠2+∠3=90°.探究一探究二探究三规范解答(证法2)连接OC,同上可证得∠2+∠3=90°.
∵PQ切☉O于点C,∴OC⊥PQ.
在Rt△PQO中,由射影定理可得OC2=PC·CQ.
利用切线长定理,有PC=AP,CQ=BQ,
∴OC2=AP·BQ.探究一探究二探究三规范解答变式训练3?
如图,AB是☉O的直径,C是☉O上一点,过点C的切线与过A,B两点的切线分别交于点E,F,AF与BE交于点P.
求证:∠EPC=∠EBF.
证明∵EA,EF,FB是☉O的切线,
∴EA=EC,FC=FB.
∵EA,FB切☉O于A,B,AB是直径,探究一探究二探究三规范解答圆中比例线段的综合问题
典例
如图,☉O的直径AB的延长线与弦CD的延长线相交于点P,E
(1)证明:DF·EF=OF·FP;
(2)当AB=2BP时,证明:OF=BF.
【审题策略】(1)证明△OFE∽△DFP后利用对应边成比例求解;
(2)利用相交弦定理化简证明.探究一探究二探究三规范解答探究一探究二探究三规范解答【答题模板】(1)第1步:作辅助线;
第2步:证明两个三角形相似;
第3步:得到成比例线段,证得结论.
(2)第1步:利用相交弦定理得到成比例线段;
第2步:结合(1)的结论得到欲证线段之间关系;
第3步:整理即得所证结论.探究一探究二探究三规范解答探究一探究二探究三规范解答变式训练?
如图,P是☉O外一点,PA是切线,A为切点,割线PBC与☉O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交☉O于点E.
求证:(1)BE=EC;(2)AD·DE=2PB2.探究一探究二探究三规范解答证明
(1)因为PC=2PA,PD=DC,所以PA=PD,△PAD为等腰三角形.
连接AB,设∠PAB=∠DEB=β,∠BCE=∠BAE=α.
因为∠PAB+∠BCE=∠PAB+∠BAD=∠PAD=∠PDA=∠DEB+∠DBE,
所以β+α=β+∠DBE,
所以α=∠DBE,
即∠BCE=∠DBE,
所以BE=EC.探究一探究二探究三规范解答(2)因为AD·DE=BD·DC,PA2=PB·PC,PD=DC=PA,
所以PA2=PB·PC=PB·2PA,即PA=2PB,
所以BD·DC=(PA-PB)·PA=PA2-PB·PA=PB·PC-PB·PA=PB·(PC-PA)=PB·PA=PB·2PB=2PB2,故AD·DE=2PB2.123451.设圆内两条相交弦,其中一条弦长为8 cm,且被交点平分,另一条弦被交点分成1∶4两部分,则这条弦长是( )
A.2 cm B.8 cm C.10 cm D.12 cm
所以这条弦长为10 cm.
答案C12345123453.
如图所示,PA,PB是☉O的两条切线,A,B为切点,连接OP交AB于C,连接OA,OB,则图中等腰三角形、直角三角形的个数分别为( )
A.1,2 B.2,2 C.2,6 D.1,6
解析∵PA,PB为☉O的切线,∴OA⊥AP,OB⊥PB,PA=PB,OP平分∠APB,∴OP⊥AB.
∴直角三角形有6个:△OAP,△OBP,△OCA,△OCB,△ACP,△CBP;等腰三角形有2个:△OAB,△ABP.
答案C123454.
如图所示,过点P的直线与☉O相交于A,B两点.若PA=1,AB=2,PO=3,则☉O的半径等于 .?
解析设圆O的半径为r,则由割线定理可得PA·PB=(PO+r)·(PO-r),即32-r2=1×(1+2),解得r= (负值舍去).
答案123455.
如图所示,在两圆公共弦AB上,任取一点G,过点G作直线交☉O1于点C,D,交☉O2于点E,F.
求证:CG·ED=EG·CF.
证明∵AB与CD是☉O1的相交弦,∴AG·BG=CG·DG.
同理在☉O2中,AG·BG=EG·FG.
∴CG·DG=EG·FG,
(1)文字叙述:圆内的两条相交弦,被交点分成的两条线段长的积相等.
(2)图形及符号表示:如图所示,AB,CD是☉O的两条弦,AB,CD相交于点P,则PA·PB=PC·PD.1234123412342.割线定理
(1)文字叙述:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.
(2)图形及符号表示:如图,PA和PC是圆O的两条割线,与圆分别交于点B,A和D,C,则PA·PB=PC·PD.1234做一做2 如图,圆O的两条割线PAB与PCD,若PC=2,CD=5,则PA·PB= .?
解析由割线定理可得PA·PB=PC·PD,于是PA·PB=2×(2+5)=14.
答案1412343.切割线定理
(1)文字叙述:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.
(2)图形及符号表示:如图,从☉O外一点P引圆的切线PA和割线PBC,A是切点,则PA2=PB·PC.1234做一做3 如图,PM是圆O的切线,PAB是圆O的割线,若PM=4,PA=2,则AB= .?解析由切割线定理可得PM2=PA·PB,于是42=2(2+AB),解得AB=6.
答案612344.切线长定理
(1)文字叙述:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
(2)图形及符号表示:如图,PA,PB分别与☉O相切于点A,B,则PA=PB,∠OPA=∠OPB.12341234做一做4?
如图所示,PM,PN是圆O的两条切线,切点为M,N,若∠MON=110°,则∠MPO= .?
解析由切线长定理可知PM=PN,∠OPN=∠OPM,而∠MON=110°,所以∠MPN=70°,从而∠MPO=35°.
答案35°1234思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)若圆O的两条割线是PAB与PCD,则有PA·AB=PC·CD. ( )
(2)如果AB,CD是☉O的两条相交弦,交点为P,且AB被点P平分,那么PA是PC与PD的比例中项. ( )
(3)如果圆的一条弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项. ( )
(4)如果PAB,PCD是☉O的两条割线,且PA=PC,那么PB与PD相等. ( )
答案(1)× (2)√ (3)√ (4)√探究一探究二探究三规范解答探究一相交弦定理的应用?
【例1】如图,在圆O中,M,N是弦AB的三等分点,弦CD,CE分别经过点M,N.若CM=2,MD=4,CN=3,则线段NE的长为( )探究一探究二探究三规范解答探究一探究二探究三规范解答变式训练1?
如图,AC为☉O的直径,弦BD⊥AC于点P,PC=2,PA=8,则tan∠ACD的值为 .?
解析∵AC为☉O的直径,弦BD⊥AC,∴PB=PD,∠APB=90°.
由相交弦定理得PB·PD=PA·PC,即PB2=8×2=16,∴PB=4.
答案2探究一探究二探究三规范解答探究二切割线定理的应用?
【例2】
如图,AD为☉O的直径,AB为☉O的切线,割线BMN交AD的延长线于C,且BM=MN=NC,AB=2
求:(1)BC的长;(2)☉O的半径r.
分析对于(1),可由切割线定理求得BM的长,从而求出BC的长度;对于(2),应由割线定理求得半径.探究一探究二探究三规范解答探究一探究二探究三规范解答探究一探究二探究三规范解答变式训练2?
如图,AB切☉O于B,ACD为割线,E为 的中点,BE交DC于F,求证:AF2=AC·AD.
证明连接BC,BD.∵E为 的中点,
∴∠DBE=∠CBE.
又AB是☉O的切线,
∴∠ABC=∠CDB.
∴∠ABC+∠CBE=∠DBE+∠CDB,即∠ABF=∠AFB.∴AB=AF.
又AB是☉O的切线,ACD为割线,由切割线定理可知AC·AD=AB2,
∴AF2=AC·AD.探究一探究二探究三规范解答探究三切线长定理的应用?
【例3】
如图,已知AB是☉O的直径,C为圆上任意一点,过点C的切线分别与过A,B两点的切线交于P,Q.求证:AB2=4AP·BQ.
分析一种思路是证明△AOP∽△BQO,通过对应边成比例结合切线长定理进行证明;另一种思路是在Rt△POQ中,利用射影定理结合切线长定理进行证明.探究一探究二探究三规范解答证明(证法1)
连接OP,OQ,如图.
∵AP,PQ,BQ为☉O的切线,
∴∠1=∠2,∠3=∠4.
∵AP,BQ为☉O的切线,AB为直径,
∴AB⊥AP,AB⊥BQ,
∴AP∥BQ.
∴∠A=∠B=90°,∠1+∠2+∠3+∠4=180°.
∴∠1+∠4=∠2+∠3=90°.探究一探究二探究三规范解答(证法2)连接OC,同上可证得∠2+∠3=90°.
∵PQ切☉O于点C,∴OC⊥PQ.
在Rt△PQO中,由射影定理可得OC2=PC·CQ.
利用切线长定理,有PC=AP,CQ=BQ,
∴OC2=AP·BQ.探究一探究二探究三规范解答变式训练3?
如图,AB是☉O的直径,C是☉O上一点,过点C的切线与过A,B两点的切线分别交于点E,F,AF与BE交于点P.
求证:∠EPC=∠EBF.
证明∵EA,EF,FB是☉O的切线,
∴EA=EC,FC=FB.
∵EA,FB切☉O于A,B,AB是直径,探究一探究二探究三规范解答圆中比例线段的综合问题
典例
如图,☉O的直径AB的延长线与弦CD的延长线相交于点P,E
(1)证明:DF·EF=OF·FP;
(2)当AB=2BP时,证明:OF=BF.
【审题策略】(1)证明△OFE∽△DFP后利用对应边成比例求解;
(2)利用相交弦定理化简证明.探究一探究二探究三规范解答探究一探究二探究三规范解答【答题模板】(1)第1步:作辅助线;
第2步:证明两个三角形相似;
第3步:得到成比例线段,证得结论.
(2)第1步:利用相交弦定理得到成比例线段;
第2步:结合(1)的结论得到欲证线段之间关系;
第3步:整理即得所证结论.探究一探究二探究三规范解答探究一探究二探究三规范解答变式训练?
如图,P是☉O外一点,PA是切线,A为切点,割线PBC与☉O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交☉O于点E.
求证:(1)BE=EC;(2)AD·DE=2PB2.探究一探究二探究三规范解答证明
(1)因为PC=2PA,PD=DC,所以PA=PD,△PAD为等腰三角形.
连接AB,设∠PAB=∠DEB=β,∠BCE=∠BAE=α.
因为∠PAB+∠BCE=∠PAB+∠BAD=∠PAD=∠PDA=∠DEB+∠DBE,
所以β+α=β+∠DBE,
所以α=∠DBE,
即∠BCE=∠DBE,
所以BE=EC.探究一探究二探究三规范解答(2)因为AD·DE=BD·DC,PA2=PB·PC,PD=DC=PA,
所以PA2=PB·PC=PB·2PA,即PA=2PB,
所以BD·DC=(PA-PB)·PA=PA2-PB·PA=PB·PC-PB·PA=PB·(PC-PA)=PB·PA=PB·2PB=2PB2,故AD·DE=2PB2.123451.设圆内两条相交弦,其中一条弦长为8 cm,且被交点平分,另一条弦被交点分成1∶4两部分,则这条弦长是( )
A.2 cm B.8 cm C.10 cm D.12 cm
所以这条弦长为10 cm.
答案C12345123453.
如图所示,PA,PB是☉O的两条切线,A,B为切点,连接OP交AB于C,连接OA,OB,则图中等腰三角形、直角三角形的个数分别为( )
A.1,2 B.2,2 C.2,6 D.1,6
解析∵PA,PB为☉O的切线,∴OA⊥AP,OB⊥PB,PA=PB,OP平分∠APB,∴OP⊥AB.
∴直角三角形有6个:△OAP,△OBP,△OCA,△OCB,△ACP,△CBP;等腰三角形有2个:△OAB,△ABP.
答案C123454.
如图所示,过点P的直线与☉O相交于A,B两点.若PA=1,AB=2,PO=3,则☉O的半径等于 .?
解析设圆O的半径为r,则由割线定理可得PA·PB=(PO+r)·(PO-r),即32-r2=1×(1+2),解得r= (负值舍去).
答案123455.
如图所示,在两圆公共弦AB上,任取一点G,过点G作直线交☉O1于点C,D,交☉O2于点E,F.
求证:CG·ED=EG·CF.
证明∵AB与CD是☉O1的相交弦,∴AG·BG=CG·DG.
同理在☉O2中,AG·BG=EG·FG.
∴CG·DG=EG·FG,
