高中数学人教A版选修4-1课件:3.2 平面与圆柱面的截线 :20张PPT
文档属性
| 名称 | 高中数学人教A版选修4-1课件:3.2 平面与圆柱面的截线 :20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 545.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 00:00:00 | ||
图片预览







文档简介
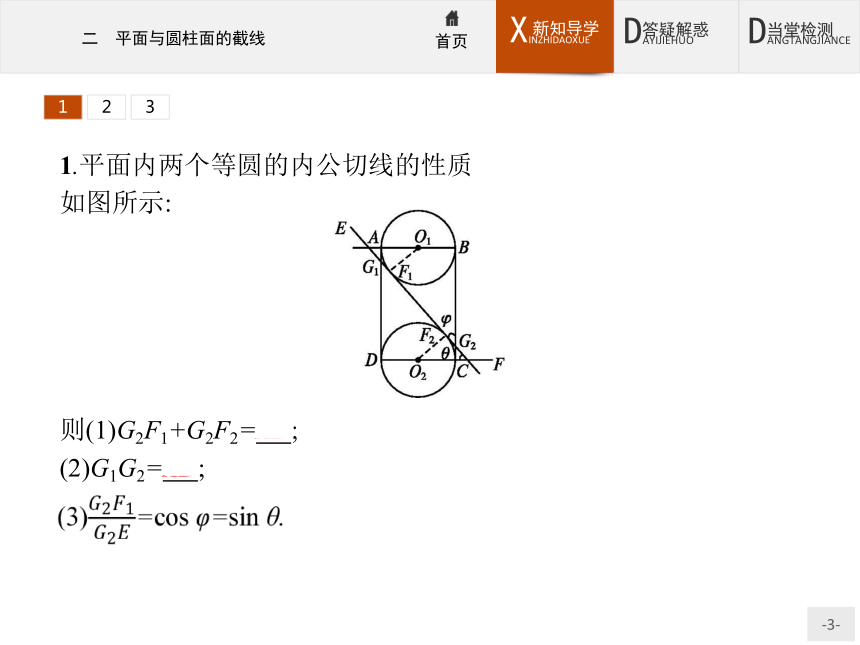
课件20张PPT。二 平面与圆柱面的截线1231.平面内两个等圆的内公切线的性质
如图所示:
则(1)G2F1+G2F2=AD;
(2)G1G2=AD;1232.定理1
圆柱形物体的斜截口是椭圆.
做一做1 用一个平面截圆柱体,截口形状不可能是 ( )?
A.椭圆 B.矩形 C.圆 D.三角形
解析用任何平面截圆柱体,截口形状都不可能是三角形.
答案D1233.椭圆
(1)椭圆中的有关概念
如图,F1,F2是椭圆的焦点,B1B2是F1F2的中垂线.我们把A1A2叫做椭圆的长轴,B1B2叫做椭圆的短轴,F1F2叫做椭圆的焦距.如果长轴长123(2)椭圆的性质
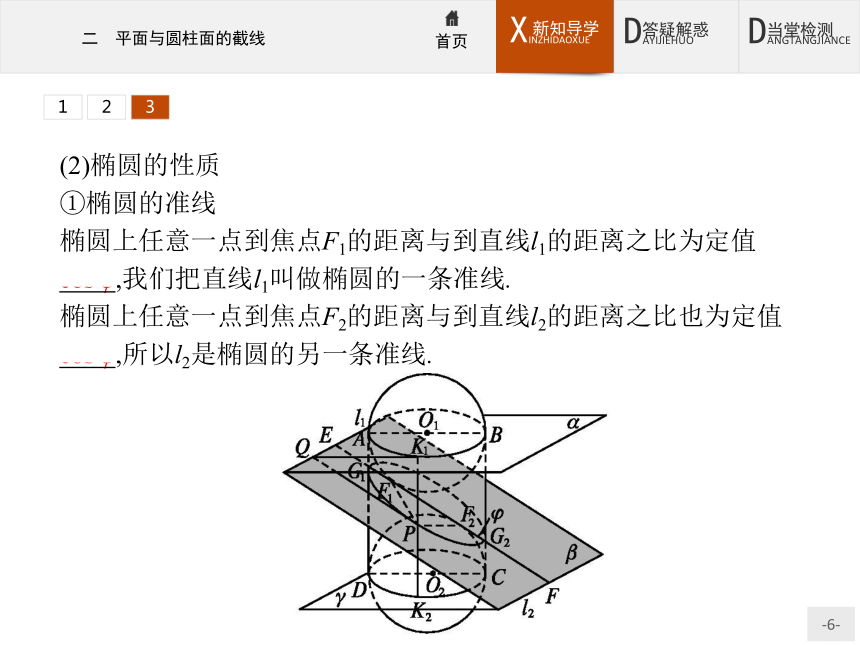
①椭圆的准线
椭圆上任意一点到焦点F1的距离与到直线l1的距离之比为定值
cos φ,我们把直线l1叫做椭圆的一条准线.?
椭圆上任意一点到焦点F2的距离与到直线l2的距离之比也为定值cos φ,所以l2是椭圆的另一条准线.?123②椭圆的离心率
记e=cos φ,我们把e叫做椭圆的离心率(其中φ是截面β与圆柱母线的交角).123123思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)圆柱形物体的截口是椭圆. ( )
(2)椭圆的离心率越大,椭圆就越扁. ( )
(3)任何椭圆都有两条准线. ( )
(4)椭圆上任意一点到焦点的距离与其到准线的距离之比为定值. ( )
(5)当圆柱形物体的斜截口是椭圆时,该椭圆的短轴长等于圆柱底面圆的直径. ( )
答案(1)× (2)√ (3)√ (4)× (5)√探究一探究二探究一平面内两个等圆的内公切线的性质应用?
【例1】
如图,AB,CD是两个半径为2的等圆的直径,AB∥CD,AD,BC与两圆相切,作两圆公切线EF,切点为F1,F2,交BA,DC的延长线于E,F两点,交AD于G1,交BC于G2,设EF与BC,CD的交角分别为φ,θ.当θ=30°时,则探究一探究二探究一探究二探究二椭圆几何性质的求解?
【例2】已知一个圆柱的底面半径r=6,一截割平面β与圆柱母线所成的角为45°,求此截割面的两个焦球球心距离,并求出截线椭圆的长轴长、短轴长和离心率e.
分析根据截割面的两个焦球与椭圆长轴、短轴之间的关系进行求解.探究一探究二探究一探究二123451.圆柱形物体的截口可能是( )
A.抛物线 B.双曲线
C.直线 D.椭圆或圆
解析当截面与圆柱底面平行时,截口是圆;当截面与圆柱底面不平行时,截口是椭圆.
答案D123452.一组底面为同心圆的圆柱被一平面所截,截口椭圆具有 ( )
A.相同的长轴 B.相同的焦点
C.相同的准线 D.相同的离心率
解析因为底面半径大小不等,所以长轴不同.嵌入的Dandelin球不同,则焦点不同,准线也不同,而平面与圆柱的母线夹角相同,故离心率相同.
答案D1234512345123455.如图所示,设两个焦点的距离F1F2=2c,两个端点的距离G1G2=2a,求证:l1与l2之间的距离为12345
如图所示:
则(1)G2F1+G2F2=AD;
(2)G1G2=AD;1232.定理1
圆柱形物体的斜截口是椭圆.
做一做1 用一个平面截圆柱体,截口形状不可能是 ( )?
A.椭圆 B.矩形 C.圆 D.三角形
解析用任何平面截圆柱体,截口形状都不可能是三角形.
答案D1233.椭圆
(1)椭圆中的有关概念
如图,F1,F2是椭圆的焦点,B1B2是F1F2的中垂线.我们把A1A2叫做椭圆的长轴,B1B2叫做椭圆的短轴,F1F2叫做椭圆的焦距.如果长轴长123(2)椭圆的性质
①椭圆的准线
椭圆上任意一点到焦点F1的距离与到直线l1的距离之比为定值
cos φ,我们把直线l1叫做椭圆的一条准线.?
椭圆上任意一点到焦点F2的距离与到直线l2的距离之比也为定值cos φ,所以l2是椭圆的另一条准线.?123②椭圆的离心率
记e=cos φ,我们把e叫做椭圆的离心率(其中φ是截面β与圆柱母线的交角).123123思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)圆柱形物体的截口是椭圆. ( )
(2)椭圆的离心率越大,椭圆就越扁. ( )
(3)任何椭圆都有两条准线. ( )
(4)椭圆上任意一点到焦点的距离与其到准线的距离之比为定值. ( )
(5)当圆柱形物体的斜截口是椭圆时,该椭圆的短轴长等于圆柱底面圆的直径. ( )
答案(1)× (2)√ (3)√ (4)× (5)√探究一探究二探究一平面内两个等圆的内公切线的性质应用?
【例1】
如图,AB,CD是两个半径为2的等圆的直径,AB∥CD,AD,BC与两圆相切,作两圆公切线EF,切点为F1,F2,交BA,DC的延长线于E,F两点,交AD于G1,交BC于G2,设EF与BC,CD的交角分别为φ,θ.当θ=30°时,则探究一探究二探究一探究二探究二椭圆几何性质的求解?
【例2】已知一个圆柱的底面半径r=6,一截割平面β与圆柱母线所成的角为45°,求此截割面的两个焦球球心距离,并求出截线椭圆的长轴长、短轴长和离心率e.
分析根据截割面的两个焦球与椭圆长轴、短轴之间的关系进行求解.探究一探究二探究一探究二123451.圆柱形物体的截口可能是( )
A.抛物线 B.双曲线
C.直线 D.椭圆或圆
解析当截面与圆柱底面平行时,截口是圆;当截面与圆柱底面不平行时,截口是椭圆.
答案D123452.一组底面为同心圆的圆柱被一平面所截,截口椭圆具有 ( )
A.相同的长轴 B.相同的焦点
C.相同的准线 D.相同的离心率
解析因为底面半径大小不等,所以长轴不同.嵌入的Dandelin球不同,则焦点不同,准线也不同,而平面与圆柱的母线夹角相同,故离心率相同.
答案D1234512345123455.如图所示,设两个焦点的距离F1F2=2c,两个端点的距离G1G2=2a,求证:l1与l2之间的距离为12345
