高中数学北师大版必修3课件:1.5.1 估计总体的分布:32张PPT
文档属性
| 名称 | 高中数学北师大版必修3课件:1.5.1 估计总体的分布:32张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 795.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 12:36:52 | ||
图片预览









文档简介
课件32张PPT。5.1 估计总体的分布1.估计总体分布的相关概念
(1)总体分布:一般地,总体分布是指总体中个体所占的比例.
(2)样本频率分布表:是把样本数据重新汇总而成的一个表格,表中栏目有样本宽度分组(Δxi);频数(ni);频率(fi).
(3)频率分布直方图:每个小矩形的宽度为Δxi(分组的宽度),高为 ,小矩形的面积恰为相应的频率fi.通常我们称这样的图形为频率分布直方图.
(4)频率折线图:在频率分布直方图中,按照分组原则,再在左边和右边各加一个区间,从所加的左边区间的中点开始,用线段依次连接各个矩形的顶端中点,直至右边所加区间的中点,就可以得到一条折线,我们称之为频率折线图.规律总结几种表示样本分布方法的比较
(1)频率分布表:频率分布表在数量表示上比较确切,但不够直观、形象,分析数据分布的总体趋势不太方便.
(2)频率分布直方图:频率分布直方图能非常直观地表明数据分布的形状,使我们能够看到在分布表中看不清楚的数据模式.但是从直方图本身得不出原始的数据内容,也就是说,把数据表示成直方图后,原有的具体数据信息就被抹掉了.
(3)频率折线图:频率折线图的优点是它反映了数据的变化趋势.如果样本容量不断增大,分组的宽度不断缩小,那么折线图就趋向于一条光滑曲线.【做一做1】 为了引导学生树立正确的消费观,调查了学生每天零花钱的数量(钱数取整数元),容量为1 000的样本的频率分布直方图如图所示,则样本数据落在[6,14)内的频数为( )
A.780 B.680
C.648 D.460
解析:依题意知(0.02+0.08+x+0.03×2)×4=1,故x=0.09.
数据落在[6,14)内的频率为(0.08+0.09)×4=0.68,
因此频数为0.68×1 000=680.故选B.
答案:B2.频率分布表、频率分布直方图、频率折线图的画法
(1)频率分布表的画法步骤
①计算数据中最大值与最小值的差称为极差,算出极差就知道数据变动的范围;③决定分点;
④列频率分布表,数据落在第i个小组内的个数为频数ni;每小组的频数与数据总数的比值叫作这一小组的频率fi,算出各小组的频率;为方便画图还需计算出 填入表中.(2)频率分布直方图的画法步骤
①列频率分布表;
②画坐标系,以横轴表示样本的分组,以纵轴表示频率与分组的宽度的比 ;
③按照频率分布表中的数据作出各个小矩形,即得频率分布直方图.
(3)频率折线图的画法步骤
①绘制频率分布直方图;
②取点:取各个小矩形的顶端的中点,再在原分组的左、右两边各增加一个小区间,取其中点(这两个端点没有实际意义);
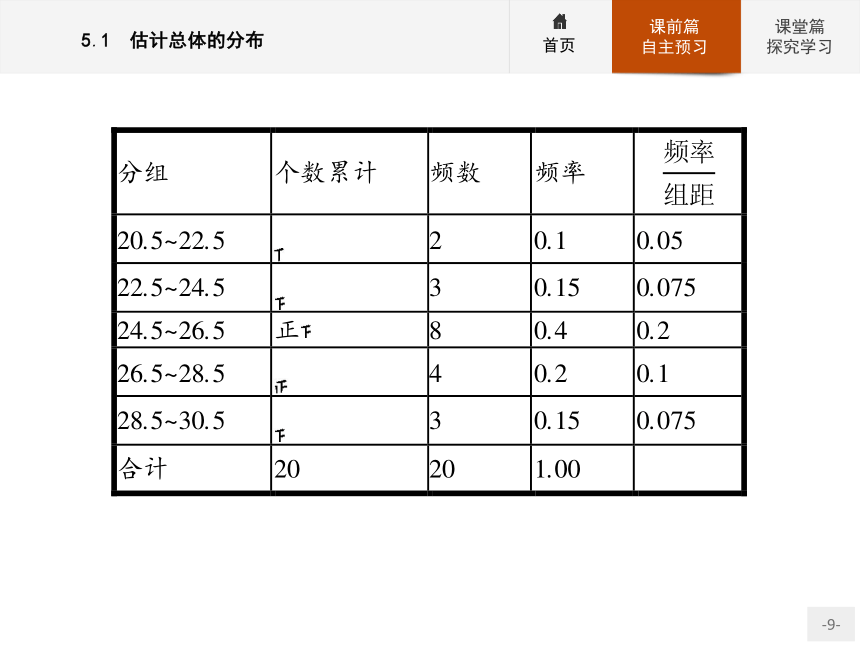
③连线:用直线段顺次连接这些中点,就得到频率折线图.【做一做2】 已知一个样本:30,29,26,24,25,27,26,22,24,25,26, 28,25,21,23,25,27,29,25,28.
(1)列出样本的频率分布表.
(2)画出频率分布直方图和频率折线图.
解:(1)计算极差:30-21=9.
决定组距和组数:取组距为2.所以共分5组.
决定分点,使分点比数据多一位小数.
并把第1小组的分点减小0.5,即分成如下5组:
20.5~22.5,22.5~24.5,24.5~26.5,26.5~28.5,28.5~30.5.
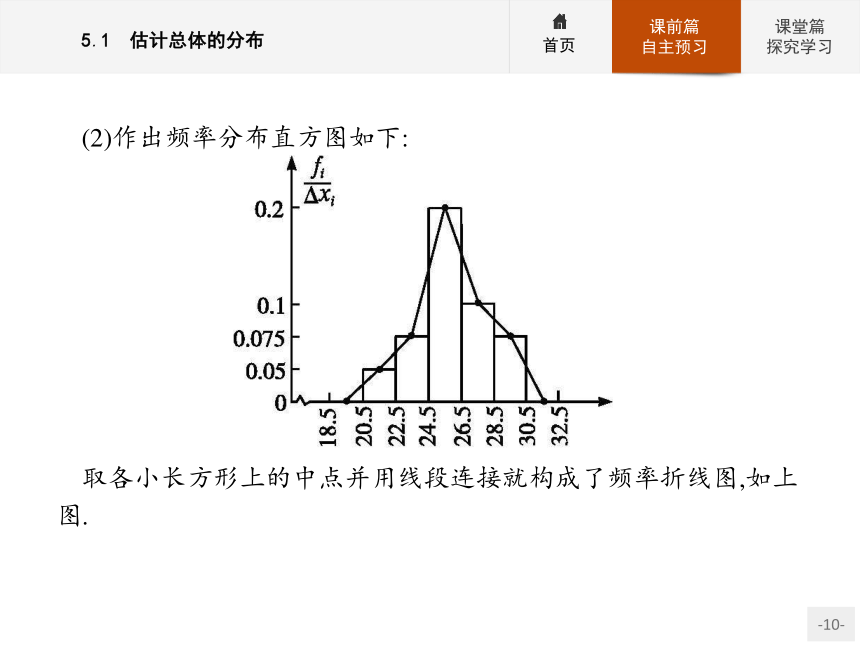
列出频率分布表如下:(2)作出频率分布直方图如下:
?
取各小长方形上的中点并用线段连接就构成了频率折线图,如上图.思考辨析
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)频率分布直方图中小长方形的高表示取某数的频率. ( )
(2)频率分布直方图中所有小长方形的面积之和为1. ( )
(3)频率分布直方图中小长方形的面积等于该组的频率×组距. ( )
(4)频率分布折线图能反映数据的增减趋势. ( )
答案:(1)× (2)√ (3)× (4)√探究一探究二思维辨析当堂检测频率分布直方图与折线图的概念及画法
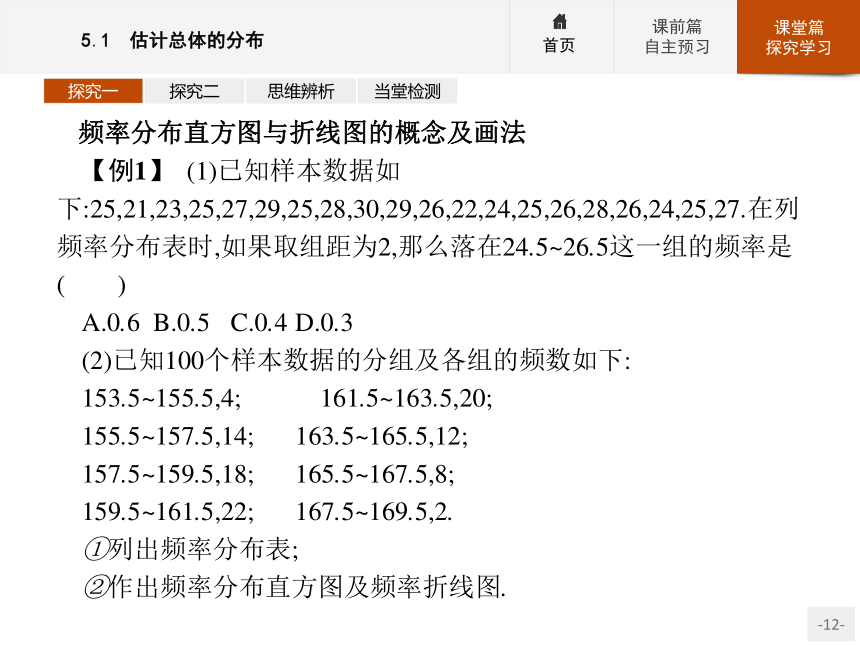
【例1】 (1)已知样本数据如下:25,21,23,25,27,29,25,28,30,29,26,22,24,25,26,28,26,24,25,27.在列频率分布表时,如果取组距为2,那么落在24.5~26.5这一组的频率是( )
A.0.6 B.0.5 C.0.4 D.0.3
(2)已知100个样本数据的分组及各组的频数如下:
153.5~155.5,4; 161.5~163.5,20;
155.5~157.5,14; 163.5~165.5,12;
157.5~159.5,18; 165.5~167.5,8;
159.5~161.5,22; 167.5~169.5,2.
①列出频率分布表;
②作出频率分布直方图及频率折线图.探究一探究二思维辨析当堂检测(1)答案:C
(2)解:①频率分布表如下:探究一探究二思维辨析当堂检测②频率分布直方图和频率折线图如图所示. 探究一探究二思维辨析当堂检测反思感悟1.可按照画频率分布直方图的一般步骤画出频率分布直方图,特别要注意的是纵坐标表示的是 ,而不是频率.
2.对数据进行分组时,确定好分点是关键,通常有两种方法:
(1)改变数据位数,若数据为整数,则分点数据减去0.5;若数据是小数点后有1位的数,则分点数据减去0.05,依此类推.
(2)不改变数据位数,但要注意分组后,每组的起点数据包含在该组内,终点数据不包含在该组内.
3.画频率折线图时,应先作出频率分布直方图,再在最左边和最右边各添加一个区间,依次取出矩形顶端的中点,然后即可画出频率折线图.探究一探究二思维辨析当堂检测变式训练1有一个容量为50的样本,数据分组及各组的频数如下:12.5~15.5,3;15.5~18.5,8;18.5~21.5,9;21.5~24.5,11;24.5~27.5,10;27.5~30.5,5;30.5~33.5,4.
(1)列出样本频率分布图表;
(2)画出频率分布直方图和频率分布折线图.探究一探究二思维辨析当堂检测解:(1)频率分布表如下: 探究一探究二思维辨析当堂检测(2)频率分布直方图和频率分布折线图如图所示.探究一探究二思维辨析当堂检测频率分布直方图的应用
【例2】 (1)如图,有一频率分布直方图,图中x的值为( )
A.0.4 B.0.2
C.0.04 D.0.02探究一探究二思维辨析当堂检测(2)某学校对高二年级一次考试成绩进行抽样分析.如图是根据抽样分析后的考试成绩绘制的频率分布直方图,其中抽样成绩的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104), [104,106].已知样本中成绩小于100分的人数是36,则样本中成绩大于或等于98分且小于104分的人数是( )
?
A.90 B.75 C.60 D.45探究一探究二思维辨析当堂检测解析:(1)在频率分布直方图中,分组的宽度为1,于是有(0.1+0.15+2x+0.35)×1=1,解得x=0.2.
(2)样本中成绩小于100分的频率为(0.050+0.100)×2=0.3.
∴样本容量为
∴样本中成绩大于或等于98分且小于104分的人数为120×(0.100+0.150+0.125)×2=90.
答案:(1)B (2)A探究一探究二思维辨析当堂检测探究一探究二思维辨析当堂检测变式训练2如图所示是总体的一个样本频率分布直方图,且在[15,18)内频数为8.
(1)求样本在[15,18)内的频率;
(2)求样本容量;
(3)若在[12,15)内的小矩形面积为0.06,求在[18,33)内的频数.探究一探究二思维辨析当堂检测解:由样本频率分布直方图可知组距为3.
(3)在[12,15)内的小矩形面积为0.06,故样本在[12,15)内的频率为0.06,故样本在[15,33)内的频数为50×(1-0.06)=47.又因为在[15,18)内的频数为8,故在[18,33)内的频数为47-8=39.探究一探究二思维辨析当堂检测未理解频率分布直方图中纵坐标的含义而致误
【典例】中小学生的视力状况受到全社会的广泛关注,某市有关部门从全市60 000名高一新生中随机抽取了400名学生,对他们的视力状况进行一次调查统计,将所得到的有关数据绘制成频率分布直方图,如图所示,从左到右五个小组的频率之比依次是5∶7∶12∶10∶6,则全市高一新生视力在[3.95,4.25]范围内的学生约有多少人?探究一探究二思维辨析当堂检测纠错心得1.在频率分布直方图中,纵坐标对应值的含义是 ,每个小长方形的面积才能代表对应各段内频率值.
2.该例题产生错误的根源就是把图中标注的0.5看成了第五组的频率,而实际上0.5×0.3=0.15才是对应的频率,因此正确认识频率分布直方图的意义是解决问题的关键.探究一探究二思维辨析当堂检测变式训练有一容量为500的样本,把数据分成7组,它的频率分布直方图如图所示,根据其频率分布直方图,请你估计数据落在15.5~24.5内的数量.解:由频率分布直方图可知,数据分成7组,其组距为3,所以数据落在15.5~18.5内的频率为0.054×3,落在18.5~21.5内的频率为0.06×3,落在21.5~24.5内的频率为0.075×3.所以数据落在15.5~24.5内的数量有500×(0.054×3+0.06×3+0.075×3)=283.5.所以估计数据落在15.5~24.5内的数量大约有284个.探究一探究二思维辨析当堂检测1.在用样本频率分布估计总体频率分布的过程中,下列说法正确的是( )
A.总体容量越大,估计越精确 B.总体容量越小,估计越精确
C.样本容量越大,估计越精确 D.样本容量越小,估计越精确
答案:C
2.有一个容量为200的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间10~12内的频数为( )
A.18 B.36
C.54 D.72
答案:B探究一探究二思维辨析当堂检测3.一个容量为35的样本数据,分组后,各组与相应频数如下:[5,10),5;[10,15),12;[15,20),7;[20,25),5;[25,30),4;[30,35),2,则样本在区间[20,35)上的频率约为( )
A.20% B.69% C.31% D.27%答案:C 4.一个容量为20的样本,数据的分组及各组的频数如下表:(其中x,y∈N+)则样本在区间10~50上的频率为 .?
答案:0.7探究一探究二思维辨析当堂检测5.从高三学生中抽取50名同学参加数学竞赛,成绩的分组及各组的频数如下
(单位:分):40~50,2;50~60,3;60~70,10;70~80,15;80~90,12;90~100,8.
(1)列出样本的频率分布表;
(2)画出频率分布直方图及频率折线图;
(3)估计成绩在60~90分的学生比例.探究一探究二思维辨析当堂检测解:(1)样本的频率分布表如下: 探究一探究二思维辨析当堂检测(2)频率分布直方图及频率折线图如图所示:(3)成绩在60~90的频率为0.2+0.3+0.24=0.74,所以可估计成绩在60~90分的学生比例为74%.
(1)总体分布:一般地,总体分布是指总体中个体所占的比例.
(2)样本频率分布表:是把样本数据重新汇总而成的一个表格,表中栏目有样本宽度分组(Δxi);频数(ni);频率(fi).
(3)频率分布直方图:每个小矩形的宽度为Δxi(分组的宽度),高为 ,小矩形的面积恰为相应的频率fi.通常我们称这样的图形为频率分布直方图.
(4)频率折线图:在频率分布直方图中,按照分组原则,再在左边和右边各加一个区间,从所加的左边区间的中点开始,用线段依次连接各个矩形的顶端中点,直至右边所加区间的中点,就可以得到一条折线,我们称之为频率折线图.规律总结几种表示样本分布方法的比较
(1)频率分布表:频率分布表在数量表示上比较确切,但不够直观、形象,分析数据分布的总体趋势不太方便.
(2)频率分布直方图:频率分布直方图能非常直观地表明数据分布的形状,使我们能够看到在分布表中看不清楚的数据模式.但是从直方图本身得不出原始的数据内容,也就是说,把数据表示成直方图后,原有的具体数据信息就被抹掉了.
(3)频率折线图:频率折线图的优点是它反映了数据的变化趋势.如果样本容量不断增大,分组的宽度不断缩小,那么折线图就趋向于一条光滑曲线.【做一做1】 为了引导学生树立正确的消费观,调查了学生每天零花钱的数量(钱数取整数元),容量为1 000的样本的频率分布直方图如图所示,则样本数据落在[6,14)内的频数为( )
A.780 B.680
C.648 D.460
解析:依题意知(0.02+0.08+x+0.03×2)×4=1,故x=0.09.
数据落在[6,14)内的频率为(0.08+0.09)×4=0.68,
因此频数为0.68×1 000=680.故选B.
答案:B2.频率分布表、频率分布直方图、频率折线图的画法
(1)频率分布表的画法步骤
①计算数据中最大值与最小值的差称为极差,算出极差就知道数据变动的范围;③决定分点;
④列频率分布表,数据落在第i个小组内的个数为频数ni;每小组的频数与数据总数的比值叫作这一小组的频率fi,算出各小组的频率;为方便画图还需计算出 填入表中.(2)频率分布直方图的画法步骤
①列频率分布表;
②画坐标系,以横轴表示样本的分组,以纵轴表示频率与分组的宽度的比 ;
③按照频率分布表中的数据作出各个小矩形,即得频率分布直方图.
(3)频率折线图的画法步骤
①绘制频率分布直方图;
②取点:取各个小矩形的顶端的中点,再在原分组的左、右两边各增加一个小区间,取其中点(这两个端点没有实际意义);
③连线:用直线段顺次连接这些中点,就得到频率折线图.【做一做2】 已知一个样本:30,29,26,24,25,27,26,22,24,25,26, 28,25,21,23,25,27,29,25,28.
(1)列出样本的频率分布表.
(2)画出频率分布直方图和频率折线图.
解:(1)计算极差:30-21=9.
决定组距和组数:取组距为2.所以共分5组.
决定分点,使分点比数据多一位小数.
并把第1小组的分点减小0.5,即分成如下5组:
20.5~22.5,22.5~24.5,24.5~26.5,26.5~28.5,28.5~30.5.
列出频率分布表如下:(2)作出频率分布直方图如下:
?
取各小长方形上的中点并用线段连接就构成了频率折线图,如上图.思考辨析
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)频率分布直方图中小长方形的高表示取某数的频率. ( )
(2)频率分布直方图中所有小长方形的面积之和为1. ( )
(3)频率分布直方图中小长方形的面积等于该组的频率×组距. ( )
(4)频率分布折线图能反映数据的增减趋势. ( )
答案:(1)× (2)√ (3)× (4)√探究一探究二思维辨析当堂检测频率分布直方图与折线图的概念及画法
【例1】 (1)已知样本数据如下:25,21,23,25,27,29,25,28,30,29,26,22,24,25,26,28,26,24,25,27.在列频率分布表时,如果取组距为2,那么落在24.5~26.5这一组的频率是( )
A.0.6 B.0.5 C.0.4 D.0.3
(2)已知100个样本数据的分组及各组的频数如下:
153.5~155.5,4; 161.5~163.5,20;
155.5~157.5,14; 163.5~165.5,12;
157.5~159.5,18; 165.5~167.5,8;
159.5~161.5,22; 167.5~169.5,2.
①列出频率分布表;
②作出频率分布直方图及频率折线图.探究一探究二思维辨析当堂检测(1)答案:C
(2)解:①频率分布表如下:探究一探究二思维辨析当堂检测②频率分布直方图和频率折线图如图所示. 探究一探究二思维辨析当堂检测反思感悟1.可按照画频率分布直方图的一般步骤画出频率分布直方图,特别要注意的是纵坐标表示的是 ,而不是频率.
2.对数据进行分组时,确定好分点是关键,通常有两种方法:
(1)改变数据位数,若数据为整数,则分点数据减去0.5;若数据是小数点后有1位的数,则分点数据减去0.05,依此类推.
(2)不改变数据位数,但要注意分组后,每组的起点数据包含在该组内,终点数据不包含在该组内.
3.画频率折线图时,应先作出频率分布直方图,再在最左边和最右边各添加一个区间,依次取出矩形顶端的中点,然后即可画出频率折线图.探究一探究二思维辨析当堂检测变式训练1有一个容量为50的样本,数据分组及各组的频数如下:12.5~15.5,3;15.5~18.5,8;18.5~21.5,9;21.5~24.5,11;24.5~27.5,10;27.5~30.5,5;30.5~33.5,4.
(1)列出样本频率分布图表;
(2)画出频率分布直方图和频率分布折线图.探究一探究二思维辨析当堂检测解:(1)频率分布表如下: 探究一探究二思维辨析当堂检测(2)频率分布直方图和频率分布折线图如图所示.探究一探究二思维辨析当堂检测频率分布直方图的应用
【例2】 (1)如图,有一频率分布直方图,图中x的值为( )
A.0.4 B.0.2
C.0.04 D.0.02探究一探究二思维辨析当堂检测(2)某学校对高二年级一次考试成绩进行抽样分析.如图是根据抽样分析后的考试成绩绘制的频率分布直方图,其中抽样成绩的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104), [104,106].已知样本中成绩小于100分的人数是36,则样本中成绩大于或等于98分且小于104分的人数是( )
?
A.90 B.75 C.60 D.45探究一探究二思维辨析当堂检测解析:(1)在频率分布直方图中,分组的宽度为1,于是有(0.1+0.15+2x+0.35)×1=1,解得x=0.2.
(2)样本中成绩小于100分的频率为(0.050+0.100)×2=0.3.
∴样本容量为
∴样本中成绩大于或等于98分且小于104分的人数为120×(0.100+0.150+0.125)×2=90.
答案:(1)B (2)A探究一探究二思维辨析当堂检测探究一探究二思维辨析当堂检测变式训练2如图所示是总体的一个样本频率分布直方图,且在[15,18)内频数为8.
(1)求样本在[15,18)内的频率;
(2)求样本容量;
(3)若在[12,15)内的小矩形面积为0.06,求在[18,33)内的频数.探究一探究二思维辨析当堂检测解:由样本频率分布直方图可知组距为3.
(3)在[12,15)内的小矩形面积为0.06,故样本在[12,15)内的频率为0.06,故样本在[15,33)内的频数为50×(1-0.06)=47.又因为在[15,18)内的频数为8,故在[18,33)内的频数为47-8=39.探究一探究二思维辨析当堂检测未理解频率分布直方图中纵坐标的含义而致误
【典例】中小学生的视力状况受到全社会的广泛关注,某市有关部门从全市60 000名高一新生中随机抽取了400名学生,对他们的视力状况进行一次调查统计,将所得到的有关数据绘制成频率分布直方图,如图所示,从左到右五个小组的频率之比依次是5∶7∶12∶10∶6,则全市高一新生视力在[3.95,4.25]范围内的学生约有多少人?探究一探究二思维辨析当堂检测纠错心得1.在频率分布直方图中,纵坐标对应值的含义是 ,每个小长方形的面积才能代表对应各段内频率值.
2.该例题产生错误的根源就是把图中标注的0.5看成了第五组的频率,而实际上0.5×0.3=0.15才是对应的频率,因此正确认识频率分布直方图的意义是解决问题的关键.探究一探究二思维辨析当堂检测变式训练有一容量为500的样本,把数据分成7组,它的频率分布直方图如图所示,根据其频率分布直方图,请你估计数据落在15.5~24.5内的数量.解:由频率分布直方图可知,数据分成7组,其组距为3,所以数据落在15.5~18.5内的频率为0.054×3,落在18.5~21.5内的频率为0.06×3,落在21.5~24.5内的频率为0.075×3.所以数据落在15.5~24.5内的数量有500×(0.054×3+0.06×3+0.075×3)=283.5.所以估计数据落在15.5~24.5内的数量大约有284个.探究一探究二思维辨析当堂检测1.在用样本频率分布估计总体频率分布的过程中,下列说法正确的是( )
A.总体容量越大,估计越精确 B.总体容量越小,估计越精确
C.样本容量越大,估计越精确 D.样本容量越小,估计越精确
答案:C
2.有一个容量为200的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间10~12内的频数为( )
A.18 B.36
C.54 D.72
答案:B探究一探究二思维辨析当堂检测3.一个容量为35的样本数据,分组后,各组与相应频数如下:[5,10),5;[10,15),12;[15,20),7;[20,25),5;[25,30),4;[30,35),2,则样本在区间[20,35)上的频率约为( )
A.20% B.69% C.31% D.27%答案:C 4.一个容量为20的样本,数据的分组及各组的频数如下表:(其中x,y∈N+)则样本在区间10~50上的频率为 .?
答案:0.7探究一探究二思维辨析当堂检测5.从高三学生中抽取50名同学参加数学竞赛,成绩的分组及各组的频数如下
(单位:分):40~50,2;50~60,3;60~70,10;70~80,15;80~90,12;90~100,8.
(1)列出样本的频率分布表;
(2)画出频率分布直方图及频率折线图;
(3)估计成绩在60~90分的学生比例.探究一探究二思维辨析当堂检测解:(1)样本的频率分布表如下: 探究一探究二思维辨析当堂检测(2)频率分布直方图及频率折线图如图所示:(3)成绩在60~90的频率为0.2+0.3+0.24=0.74,所以可估计成绩在60~90分的学生比例为74%.
