高中数学北师大版必修3课件:3.1.1-3.1.2 频率与概率 生活中的概率 :18张PPT
文档属性
| 名称 | 高中数学北师大版必修3课件:3.1.1-3.1.2 频率与概率 生活中的概率 :18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 317.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 12:32:43 | ||
图片预览





文档简介
课件18张PPT。1.1 频率与概率
1.2 生活中的概率1.频率
(1)在相同条件S下重复n次试验,事件A出现了m次,称n次试验中事件A出现的次数m为事件A的频数,称事件A出现的比例fn(A)= 为事件A出现的频率.
(2)频率的性质
①频率反映了一个随机事件出现的频繁程度;
②频率是随机的;
③频率的取值范围是[0,1].
【做一做1】 在一次考试中,某班学生有80%及格,80%是 .(填“概率”或“频率”)?
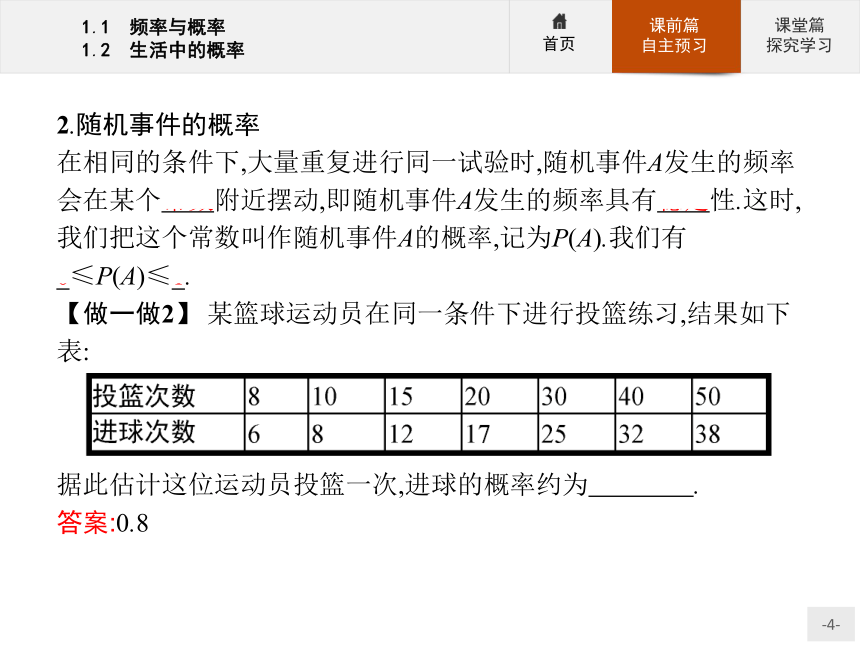
答案:频率2.随机事件的概率
在相同的条件下,大量重复进行同一试验时,随机事件A发生的频率会在某个常数附近摆动,即随机事件A发生的频率具有稳定性.这时,我们把这个常数叫作随机事件A的概率,记为P(A).我们有0≤P(A)≤1.
【做一做2】 某篮球运动员在同一条件下进行投篮练习,结果如下表:据此估计这位运动员投篮一次,进球的概率约为 .?
答案:0.83.生活中的概率
概率和日常生活有着密切的联系,对于生活中的随机事件,我们可以利用概率知识作出合理的判断与决策.
名师点拨概率是描述随机事件发生的可能性大小的度量,它已经渗透到人们的日常生活中,成为一个常用的词汇,任何事件的概率均是0~1之间的一个数,它度量该事件发生的可能性大小.小概率事件(概率接近0)很少发生,而大概率事件(概率接近1)则经常发生.
【做一做3】 某工厂生产的产品合格率是99.99%,这说明( )
A.该厂生产的10 000件产品中不合格的产品一定有1件
B.该厂生产的10 000件产品中合格的产品一定有9 999件
C.合格率99.99%很大,该厂生产的10 000件产品中没有不合格产品
D.该厂生产的产品合格的可能性是99.99%
答案:D思考辨析
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)随机事件没有结果. ( )
(2)在一次试验结束后,随机事件的频率是变化的. ( )
(3)概率是一个确定的数,是客观存在的,与试验次数无关. ( )
(4)频率是概率的近似值,随着试验次数的增加,频率会越来越接近概率. ( )
答案:(1)× (2)× (3)√ (4)√探究一探究二当堂检测频率与概率的关系
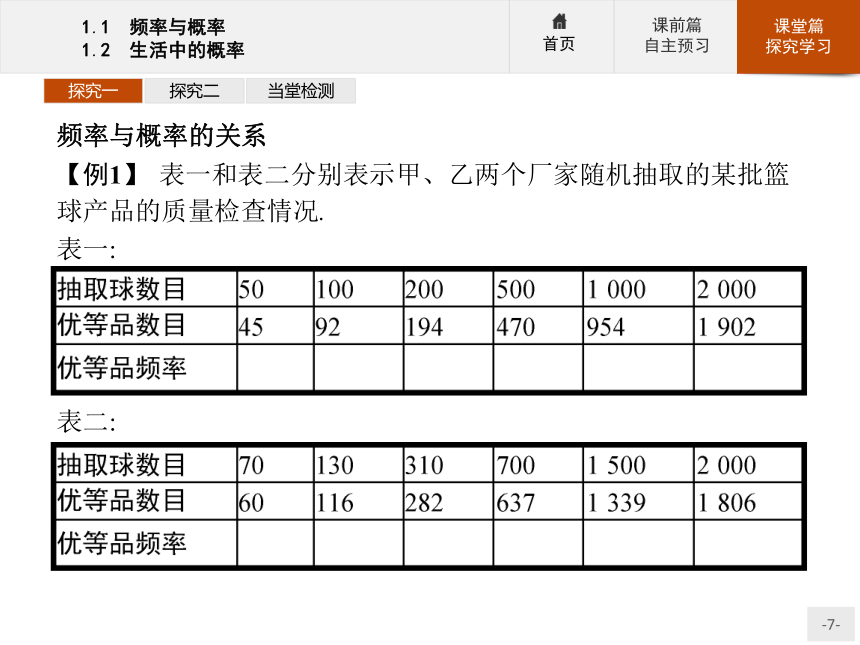
【例1】 表一和表二分别表示甲、乙两个厂家随机抽取的某批篮球产品的质量检查情况.
表一:表二: 探究一探究二当堂检测(1)分别计算表一和表二中篮球是优等品的各个频率(结果保留到小数点后两位).
(2)若从两个厂家生产的这批篮球产品中各任取一个,则质量检查为优等品的概率分别为多少?
(3)若两厂的篮球价格相同,你打算从哪一家购货?探究一探究二当堂检测解:(1)表一: 表二: 探究一探究二当堂检测(2)由(1)可知,抽取的篮球数不同,随机事件“篮球是优等品”的频率也不同.表一中的频率在常数0.95的附近摆动,则在甲厂随机抽取一个篮球检测时,质量检查为优等品的概率大约为0.95;表二中的频率在常数0.90的附近摆动,则在乙厂随机抽取一个篮球检测时,质量检查为优等品的概率大约为0.90.
(3)根据概率的定义可知:概率是从数量上反映一个随机事件发生可能性的大小.因为0.95>0.90,表示甲厂生产出来的篮球是优等品的概率更大,所以应该选择甲厂生产的篮球.探究一探究二当堂检测反思感悟1.频率本身是随机的,但当试验次数很大时,频率会在某个常数附近摆动,这个常数就是概率.
2.随机事件的概率可以从以下两方面进行求解(1)利用随机事件概率的定义,进行大量重复试验,寻找这个事件发生的频率的近似值.(2)一般先求出频率,根据频率的摆动情况估算出其概率.探究一探究二当堂检测 变式训练1某篮球运动员在最近几场大赛中罚球投篮的结果如下:(1)这位运动员投篮一次,进球的概率约是多少?
(2)这位运动员罚球100次,估计进球的次数为多少?
解:(1)这位运动员的进球频率稳定在0.75附近,从而他进球的概率约是0.75.
(2)这位运动员罚球100次,估计进球的次数为0.75×100=75.探究一探究二当堂检测对概率的正确理解
【例2】试从概率角度解释下列说法的含义:
(1)掷一枚均匀的正方体骰子得到6点的概率是 ,是否意味着把它掷6次能得到1次6点?
(2)某种病的治愈率是0.3,那么前7个人没有治愈,后3个人一定能治愈吗?如何理解治愈率是0.3?
(3)据报道:某地发生的9级地震是“千年一遇”的大地震.在这里,“千年一遇”是什么意思?探究一探究二当堂检测解:(1)把一枚均匀的骰子掷6次相当于做6次试验,因为每次试验的结果都是随机的,所以做6次试验的结果也是随机的.这就是说,每掷一次总是随机地出现一个点数,可以是1点,2点,也可以是其他点数,不一定出现6点.所以掷一枚骰子得到6点的概率是 ,并不意味着把它掷6次能得到1次6点.
(2)如果把治疗一个病人作为一次试验,治愈率是0.3,是指随着试验次数的增加,即治疗病人人数的增加,大约有30%的人能够治愈,对于一次试验来说,其结果是随机的,因此前7个病人没治愈是可能的,对后3个人来说,其结果仍然是随机的,即有可能治愈,也可能没有治愈.
(3)“千年一遇”是指0.001的概率,虽然0.001的概率比较小,但不代表没有可能;但也不能说每1 000年就一定会发生一次9级地震.探究一探究二当堂检测反思感悟1.概率是随机事件发生的可能性大小的度量,是随机事件A的本质属性.
2.由概率的定义我们可以知道随机事件A在某一独立重复试验中发生与否是随机的,但随机中含有规律性,而概率就是其规律性在数量上的反映.
3.正确理解概率的意义,要清楚它与频率的区别与联系.对具体的问题要从全局和整体上去看待,而不是局限于某一次试验或某一个具体的事件.
4.概率意义下的“可能性”是大量随机事件的客观规律,与我们日常所说的“可能”“估计”“差不多”是不同的.探究一探究二当堂检测变式训练2下列说法一定正确的是( )
A.一名篮球运动员,号称“百发百中”,若罚球三次,不会出现三投都不中的情况
B.一枚均匀的骰子掷一次得到“2点”的概率是 ,则掷6次一定会出现一次“2点”
C.若买某种彩票中一等奖的概率为万分之一,则买一万张彩票一定会中一等奖
D.随机事件发生的概率与试验次数无关
解析:A错误,会有“三投都不中”的情况发生;B错误,可能6次都不出现“2点”;C错误,概率是预测值,而该随机事件不一定会出现.
答案:D探究一探究二当堂检测1.下列说法正确的是( )
A.任何事件的概率总是在(0,1)之间
B.频率是客观存在的,与试验次数无关
C.随着试验次数的增加,频率一般会越来越接近概率
D.概率是随机的,在试验前不能确定
答案:C
2.在掷骰子游戏中共抛掷6次,则点数4( )
A.一定会出现 B.不一定会出现
C.一定出现一次 D.以上都不对
答案:B
3.小明和小颖按如下规则做游戏:桌面上放有5支铅笔,每次取1支或2支,最后取完铅笔的人获胜.你认为这个游戏规则 .(填“公平”或“不公平”)?
答案:不公平探究一探究二当堂检测4.某射手在同一条件下进行射击,结果如下表所示:(1)填写表中击中靶心的频率.
(2)这个射手射击一次,击中靶心的概率约是多少?
解:(1)表中依次填入的数据为0.80,0.95,0.88,0.92,0.89,0.91.
(2)随着射击次数的增加,击中靶心的频率逐渐趋于0.9.
所以这个射手射击一次,击中靶心的概率约是0.9.
(1)在相同条件S下重复n次试验,事件A出现了m次,称n次试验中事件A出现的次数m为事件A的频数,称事件A出现的比例fn(A)= 为事件A出现的频率.
(2)频率的性质
①频率反映了一个随机事件出现的频繁程度;
②频率是随机的;
③频率的取值范围是[0,1].
【做一做1】 在一次考试中,某班学生有80%及格,80%是 .(填“概率”或“频率”)?
答案:频率2.随机事件的概率
在相同的条件下,大量重复进行同一试验时,随机事件A发生的频率会在某个常数附近摆动,即随机事件A发生的频率具有稳定性.这时,我们把这个常数叫作随机事件A的概率,记为P(A).我们有0≤P(A)≤1.
【做一做2】 某篮球运动员在同一条件下进行投篮练习,结果如下表:据此估计这位运动员投篮一次,进球的概率约为 .?
答案:0.83.生活中的概率
概率和日常生活有着密切的联系,对于生活中的随机事件,我们可以利用概率知识作出合理的判断与决策.
名师点拨概率是描述随机事件发生的可能性大小的度量,它已经渗透到人们的日常生活中,成为一个常用的词汇,任何事件的概率均是0~1之间的一个数,它度量该事件发生的可能性大小.小概率事件(概率接近0)很少发生,而大概率事件(概率接近1)则经常发生.
【做一做3】 某工厂生产的产品合格率是99.99%,这说明( )
A.该厂生产的10 000件产品中不合格的产品一定有1件
B.该厂生产的10 000件产品中合格的产品一定有9 999件
C.合格率99.99%很大,该厂生产的10 000件产品中没有不合格产品
D.该厂生产的产品合格的可能性是99.99%
答案:D思考辨析
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)随机事件没有结果. ( )
(2)在一次试验结束后,随机事件的频率是变化的. ( )
(3)概率是一个确定的数,是客观存在的,与试验次数无关. ( )
(4)频率是概率的近似值,随着试验次数的增加,频率会越来越接近概率. ( )
答案:(1)× (2)× (3)√ (4)√探究一探究二当堂检测频率与概率的关系
【例1】 表一和表二分别表示甲、乙两个厂家随机抽取的某批篮球产品的质量检查情况.
表一:表二: 探究一探究二当堂检测(1)分别计算表一和表二中篮球是优等品的各个频率(结果保留到小数点后两位).
(2)若从两个厂家生产的这批篮球产品中各任取一个,则质量检查为优等品的概率分别为多少?
(3)若两厂的篮球价格相同,你打算从哪一家购货?探究一探究二当堂检测解:(1)表一: 表二: 探究一探究二当堂检测(2)由(1)可知,抽取的篮球数不同,随机事件“篮球是优等品”的频率也不同.表一中的频率在常数0.95的附近摆动,则在甲厂随机抽取一个篮球检测时,质量检查为优等品的概率大约为0.95;表二中的频率在常数0.90的附近摆动,则在乙厂随机抽取一个篮球检测时,质量检查为优等品的概率大约为0.90.
(3)根据概率的定义可知:概率是从数量上反映一个随机事件发生可能性的大小.因为0.95>0.90,表示甲厂生产出来的篮球是优等品的概率更大,所以应该选择甲厂生产的篮球.探究一探究二当堂检测反思感悟1.频率本身是随机的,但当试验次数很大时,频率会在某个常数附近摆动,这个常数就是概率.
2.随机事件的概率可以从以下两方面进行求解(1)利用随机事件概率的定义,进行大量重复试验,寻找这个事件发生的频率的近似值.(2)一般先求出频率,根据频率的摆动情况估算出其概率.探究一探究二当堂检测 变式训练1某篮球运动员在最近几场大赛中罚球投篮的结果如下:(1)这位运动员投篮一次,进球的概率约是多少?
(2)这位运动员罚球100次,估计进球的次数为多少?
解:(1)这位运动员的进球频率稳定在0.75附近,从而他进球的概率约是0.75.
(2)这位运动员罚球100次,估计进球的次数为0.75×100=75.探究一探究二当堂检测对概率的正确理解
【例2】试从概率角度解释下列说法的含义:
(1)掷一枚均匀的正方体骰子得到6点的概率是 ,是否意味着把它掷6次能得到1次6点?
(2)某种病的治愈率是0.3,那么前7个人没有治愈,后3个人一定能治愈吗?如何理解治愈率是0.3?
(3)据报道:某地发生的9级地震是“千年一遇”的大地震.在这里,“千年一遇”是什么意思?探究一探究二当堂检测解:(1)把一枚均匀的骰子掷6次相当于做6次试验,因为每次试验的结果都是随机的,所以做6次试验的结果也是随机的.这就是说,每掷一次总是随机地出现一个点数,可以是1点,2点,也可以是其他点数,不一定出现6点.所以掷一枚骰子得到6点的概率是 ,并不意味着把它掷6次能得到1次6点.
(2)如果把治疗一个病人作为一次试验,治愈率是0.3,是指随着试验次数的增加,即治疗病人人数的增加,大约有30%的人能够治愈,对于一次试验来说,其结果是随机的,因此前7个病人没治愈是可能的,对后3个人来说,其结果仍然是随机的,即有可能治愈,也可能没有治愈.
(3)“千年一遇”是指0.001的概率,虽然0.001的概率比较小,但不代表没有可能;但也不能说每1 000年就一定会发生一次9级地震.探究一探究二当堂检测反思感悟1.概率是随机事件发生的可能性大小的度量,是随机事件A的本质属性.
2.由概率的定义我们可以知道随机事件A在某一独立重复试验中发生与否是随机的,但随机中含有规律性,而概率就是其规律性在数量上的反映.
3.正确理解概率的意义,要清楚它与频率的区别与联系.对具体的问题要从全局和整体上去看待,而不是局限于某一次试验或某一个具体的事件.
4.概率意义下的“可能性”是大量随机事件的客观规律,与我们日常所说的“可能”“估计”“差不多”是不同的.探究一探究二当堂检测变式训练2下列说法一定正确的是( )
A.一名篮球运动员,号称“百发百中”,若罚球三次,不会出现三投都不中的情况
B.一枚均匀的骰子掷一次得到“2点”的概率是 ,则掷6次一定会出现一次“2点”
C.若买某种彩票中一等奖的概率为万分之一,则买一万张彩票一定会中一等奖
D.随机事件发生的概率与试验次数无关
解析:A错误,会有“三投都不中”的情况发生;B错误,可能6次都不出现“2点”;C错误,概率是预测值,而该随机事件不一定会出现.
答案:D探究一探究二当堂检测1.下列说法正确的是( )
A.任何事件的概率总是在(0,1)之间
B.频率是客观存在的,与试验次数无关
C.随着试验次数的增加,频率一般会越来越接近概率
D.概率是随机的,在试验前不能确定
答案:C
2.在掷骰子游戏中共抛掷6次,则点数4( )
A.一定会出现 B.不一定会出现
C.一定出现一次 D.以上都不对
答案:B
3.小明和小颖按如下规则做游戏:桌面上放有5支铅笔,每次取1支或2支,最后取完铅笔的人获胜.你认为这个游戏规则 .(填“公平”或“不公平”)?
答案:不公平探究一探究二当堂检测4.某射手在同一条件下进行射击,结果如下表所示:(1)填写表中击中靶心的频率.
(2)这个射手射击一次,击中靶心的概率约是多少?
解:(1)表中依次填入的数据为0.80,0.95,0.88,0.92,0.89,0.91.
(2)随着射击次数的增加,击中靶心的频率逐渐趋于0.9.
所以这个射手射击一次,击中靶心的概率约是0.9.
