高中数学北师大版选修4-4课件:1.1.1 平面直角坐标系与曲线方程 :31张PPT
文档属性
| 名称 | 高中数学北师大版选修4-4课件:1.1.1 平面直角坐标系与曲线方程 :31张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 754.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 12:35:24 | ||
图片预览










文档简介
课件31张PPT。第一章 坐标系§1 平面直角坐标系1.1 平面直角坐标系与曲线方程一二一、平面直角坐标系与点的坐标
在平面直角坐标系中,对于任意一点,都有唯一的有序实数对(x,y)与之对应;反之,对于任意的一个有序实数对(x,y),都有唯一的点与之对应.即在平面直角坐标系中,点和有序实数对是一一对应的.一二名师点拨1.在平面上建立直角坐标系后,平面上的点与全体有序实数对之间就建立了一一对应关系,即在给定平面直角坐标系的情况下,平面上的任意一点唯一地确定一个有序实数对;反之,任意给定一个有序实数对,它也唯一地确定平面上的一个点.
2.两点间的距离公式:在平面直角坐标系内,两点P1(x1,y1),P2(x2,y2)
之间的距离公式为|P1P2|=3.中点坐标公式:在平面直角坐标系内,若两点P1(x1,y1),P2(x2,y2)的中点为M(x,y),则x=一二做一做1 点P(1,-2)关于点A(-1,1)的对称点P'的直角坐标为( )?
A.(3,4) B.(-3,4)
C.(3,-4) D.(-3,-4)解析:设点P'的坐标为(x,y), 答案:B 一二做一做2 已知点P(-1+2m,-3-m)在第三象限,则m的取值范围是 .?解析:因为第三象限内点的坐标特征是横坐标与纵坐标均小于0,一二二、平面直角坐标系与曲线方程
在平面直角坐标系中,如果某曲线C上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:
1.曲线C上的点的坐标都是方程f(x,y)=0的解.
2.以方程f(x,y)=0的解为坐标的点都在曲线C上.
那么,方程f(x,y)=0叫作曲线C的方程,曲线C叫作方程f(x,y)=0的曲线.名师点拨求曲线方程一般有以下五个步骤:(1)建立适当的平面直角坐标系,并用(x,y)表示曲线上任意一点M的坐标;(2)写出适合条件P的点M的集合P={M|P(M)};(3)用坐标表示条件P(M),写出方程f(x,y)=0;(4)化简方程f(x,y)=0(必须等价);(5)证明以(4)中方程的解为坐标的点都在曲线上.一般地,方程的变形过程若是等价的,则步骤(5)可以省略.一二思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)若曲线C上的点都是方程f(x,y)=0的解,则曲线C是方程f(x,y)=0的曲线. ( )
(2)以方程x2+y2=4的解为坐标的点都是曲线“在y轴右侧到原点的距离等于2的点的集合”上的点. ( )
(3)已知等腰三角形ABC的底边为AB,且A(-1,1),B(3,7),则顶点C的轨迹方程为x+2y-7=0. ( )
(4)方程(x-a)2+(y-b)2=r2的曲线经过点(1,2)的充要条件是(1-a)2+(2-b)2=r2. ( )× √ × × 探究一探究二探究三思维辨析利用坐标系解决几何问题?
【例1】 已知?ABCD,求证:|AC|2+|BD|2=2(|AB|2+|AD|2).
分析:解答本题可以运用坐标方法即解析法,先在?ABCD所在的平面内建立平面直角坐标系,设出点A,B,C,D的坐标,再由距离公式完成证明.也可以运用向量的线性运算以及数量积运算加以证明.探究一探究二探究三思维辨析证法一(解析法)
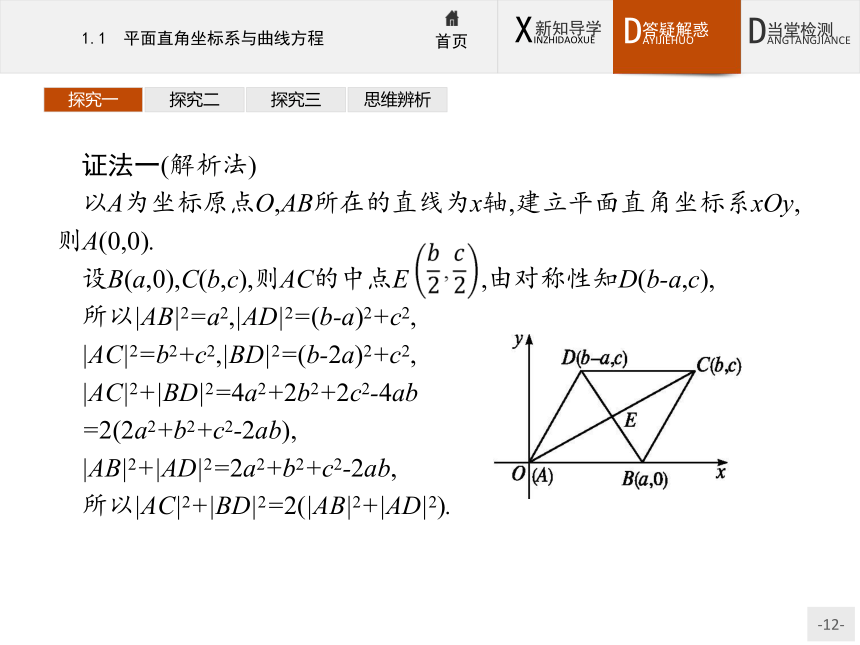
以A为坐标原点O,AB所在的直线为x轴,建立平面直角坐标系xOy,则A(0,0).
设B(a,0),C(b,c),则AC的中点E ,由对称性知D(b-a,c),
所以|AB|2=a2,|AD|2=(b-a)2+c2,
|AC|2=b2+c2,|BD|2=(b-2a)2+c2,
|AC|2+|BD|2=4a2+2b2+2c2-4ab
=2(2a2+b2+c2-2ab),
|AB|2+|AD|2=2a2+b2+c2-2ab,
所以|AC|2+|BD|2=2(|AB|2+|AD|2).探究一探究二探究三思维辨析证法二(向量法) 反思感悟建立平面直角坐标系的原则
1.如果图形有对称中心,那么可以选对称中心为原点.
2.如果图形有对称轴,那么可以选对称轴为坐标轴.
3.使图形上的特殊点尽可能多地在坐标轴上.探究一探究二探究三思维辨析变式训练1 在△ABC中,|AB|=|AC|,BD,CE分别为两腰上的高.求证:|BD|=|CE|.
证明:如图,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系.
设B(-a,0),C(a,0),A(0,h).探究一探究二探究三思维辨析求轨迹方程?
【例2】 设点A是单位圆x2+y2=1上的任意一点,l是过点A与x轴垂直的直线,点D是直线l与x轴的交点,点M在直线l上,且满足|DM|=m|DA|(m>0,且m≠1).当点A在单位圆上运动时,记点M的轨迹为曲线C.求曲线C的方程,判断曲线C为何种圆锥曲线,并求其焦点坐标.
分析:设出点M的坐标(x,y),直接利用条件求解.探究一探究二探究三思维辨析解:如图,设M(x,y),A(x0,y0),则由|DM|=m|DA|(m>0,且m≠1),可得x=x0,|y|=m|y0|,探究一探究二探究三思维辨析反思感悟求轨迹的常用方法
1.直接法:如果题目中的条件有明显的等量关系或者可以推出某个等量关系,即可用求曲线方程的五个步骤直接求解.
2.定义法:如果动点的轨迹满足某种已知曲线的定义,那么可根据定义写出轨迹方程.
3.代入法:若动点P(x,y)依赖于另一动点Q(x1,y1),而动点Q(x1,y1)又在某已知曲线上,则可先列出关于x,y,x1,y1的方程组,利用x,y表示x1,y1,把x1,y1代入已知曲线方程即为所求.
4.参数法:动点P(x,y)的横纵坐标用一个或几个参数来表示,消去参数即得其轨迹方程.探究一探究二探究三思维辨析变式训练2 在△ABC中,若BC的长度为4,中线AD的长度为3,求点A的轨迹方程.?解:取B,C所在直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系,则D(0,0),B(-2,0),C(2,0).
∴点A的轨迹方程为x2+y2=9(y≠0).探究一探究二探究三思维辨析利用坐标系解决实际问题?
【例3】 由甲导弹驱逐舰、乙导弹驱逐舰、丙综合补给舰组成的护航编队奔赴某海域执行护航任务,对商船进行护航.某日甲舰在乙舰正东6 km处,丙舰在乙舰北偏西30°,两舰相距4 km.某时刻甲舰发现商船的某种求救信号.由于乙、丙两舰比甲舰距离商船远,因此4 s后乙、丙两舰才同时发现这一信号,此信号的传播速度为1 km/s.若甲舰赶赴救援,则行进的方位角应是多少?
分析:本题求解的关键在于确定商船相对于甲舰的相对位置,因此不妨用点A,B,C表示甲舰、乙舰、丙舰,建立适当的坐标系,求出商船与甲舰的坐标,解决问题.探究一探究二探究三思维辨析解:设点A,B,C,P分别表示甲舰、乙舰、丙舰和商船.如图所示,以AB所在直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系,则A(3,0),B(-3,0),C(-5,2 ).
由题意得|PB|=|PC|,
则点P在线段BC的垂直平分线上.探究一探究二探究三思维辨析反思感悟1.由于点A,B,C的相对位置一定,解决问题的关键是如何建系,将几何位置量化,根据直线与双曲线方程求解.
2.运用坐标法解决实际问题的步骤:建系→设点→列关系式→求解数学结果→回答实际问题.探究一探究二探究三思维辨析变式训练3 已知某荒漠上有两个定点A,B,它们相距2 km,现准备在荒漠上开垦一片以AB为一条对角线的平行四边形区域建成农艺园,按照规划,围墙总长为8 km.?
(1)问:农艺园的最大面积能达到多少?
(2)该荒漠上有一条水沟l恰好经过点A,且与AB成30°的角,现要对整条水沟进行加固改造,但考虑到今后农艺园的水沟要重新改造,所以对水沟可能被农艺园围进的部分暂不加固,问:暂不加固的部分有多长?探究一探究二探究三思维辨析解:(1)设平行四边形的另两个顶点为C,D,由围墙总长为8 km,得|CA|+|CB|=4(km)>|AB|=2(km),由椭圆的定义知,点C的轨迹是以点A,B为焦点,长轴长2a=4,焦距2c=2的椭圆(去除落在直线AB上的两点).
若以AB所在直线为x轴,线段AB的垂直平分线为y轴,建立平面直角坐标系,易知点D也在此椭圆上,要使平行四边形ACBD的面积最大,则C,D为此椭圆短轴的端点,此时,面积S=2 (km2).探究一探究二探究三思维辨析探究一探究二探究三思维辨析因忽视曲线方程的意义而致误
典例已知两定点A,B,且|AB|=4,动点M满足:直线MA与MB斜率之积为常数- ,求点M的轨迹方程,并注明轨迹是什么曲线.探究一探究二探究三思维辨析正解:以AB所在直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系xOy,纠错心得1.在解本题时没有考虑到式子的意义,在 中x+2≠0,x-2≠0,即x≠±2,没有去掉相应的两个点.
2.在利用平面直角坐标系求轨迹问题时,往往会遇到去点或去掉图形的某一部分的情况,做这种题时要认真分析题目条件,求出准确的轨迹方程.探究一探究二探究三思维辨析变式训练 已知一条直线l和它上方的一个点A,点A到直线l的距离是2,一条曲线也在直线l的上方,它上面的每一点到A的距离减去到直线l的距离的差都是2,建立适当的坐标系,求这条曲线的方程.?解:取直线l为x轴,过点A且垂直于直线l的直线为y轴,建立坐标系xOy,
设点M(x,y)是曲线上任意一点,作MB⊥x轴,垂足是点B.
∵曲线在x轴的上方,∴y>0.
根据题意得|MA|-|MB|=2,1 2 3 41.已知曲线C的方程为y=x(1≤x≤5),则下列四点在曲线C上的是( )答案:D 1 2 3 42.动点P到直线x+y-4=0的距离等于它到点M(2,2)的距离,则点P的轨迹是( )
A.直线 B.椭圆
C.双曲线 D.抛物线
解析:由于点M(2,2)在直线x+y-4=0上,而|PM|等于点P到直线x+y-4=0的距离,所以动点P的轨迹是过点M且垂直于直线x+y-4=0的直线.
答案:A1 2 3 43.已知△ABC的三边a,b,c满足b2+c2=5a2,BE,CF分别为边AC,AB上的中线,则BE与CF的位置关系是 .?答案:垂直 1 2 3 44.已知△ABC的三个顶点A(-3,4),B(3,-4),C(1,7),则△ABC的形状是 .?答案:直角三角形
在平面直角坐标系中,对于任意一点,都有唯一的有序实数对(x,y)与之对应;反之,对于任意的一个有序实数对(x,y),都有唯一的点与之对应.即在平面直角坐标系中,点和有序实数对是一一对应的.一二名师点拨1.在平面上建立直角坐标系后,平面上的点与全体有序实数对之间就建立了一一对应关系,即在给定平面直角坐标系的情况下,平面上的任意一点唯一地确定一个有序实数对;反之,任意给定一个有序实数对,它也唯一地确定平面上的一个点.
2.两点间的距离公式:在平面直角坐标系内,两点P1(x1,y1),P2(x2,y2)
之间的距离公式为|P1P2|=3.中点坐标公式:在平面直角坐标系内,若两点P1(x1,y1),P2(x2,y2)的中点为M(x,y),则x=一二做一做1 点P(1,-2)关于点A(-1,1)的对称点P'的直角坐标为( )?
A.(3,4) B.(-3,4)
C.(3,-4) D.(-3,-4)解析:设点P'的坐标为(x,y), 答案:B 一二做一做2 已知点P(-1+2m,-3-m)在第三象限,则m的取值范围是 .?解析:因为第三象限内点的坐标特征是横坐标与纵坐标均小于0,一二二、平面直角坐标系与曲线方程
在平面直角坐标系中,如果某曲线C上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:
1.曲线C上的点的坐标都是方程f(x,y)=0的解.
2.以方程f(x,y)=0的解为坐标的点都在曲线C上.
那么,方程f(x,y)=0叫作曲线C的方程,曲线C叫作方程f(x,y)=0的曲线.名师点拨求曲线方程一般有以下五个步骤:(1)建立适当的平面直角坐标系,并用(x,y)表示曲线上任意一点M的坐标;(2)写出适合条件P的点M的集合P={M|P(M)};(3)用坐标表示条件P(M),写出方程f(x,y)=0;(4)化简方程f(x,y)=0(必须等价);(5)证明以(4)中方程的解为坐标的点都在曲线上.一般地,方程的变形过程若是等价的,则步骤(5)可以省略.一二思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)若曲线C上的点都是方程f(x,y)=0的解,则曲线C是方程f(x,y)=0的曲线. ( )
(2)以方程x2+y2=4的解为坐标的点都是曲线“在y轴右侧到原点的距离等于2的点的集合”上的点. ( )
(3)已知等腰三角形ABC的底边为AB,且A(-1,1),B(3,7),则顶点C的轨迹方程为x+2y-7=0. ( )
(4)方程(x-a)2+(y-b)2=r2的曲线经过点(1,2)的充要条件是(1-a)2+(2-b)2=r2. ( )× √ × × 探究一探究二探究三思维辨析利用坐标系解决几何问题?
【例1】 已知?ABCD,求证:|AC|2+|BD|2=2(|AB|2+|AD|2).
分析:解答本题可以运用坐标方法即解析法,先在?ABCD所在的平面内建立平面直角坐标系,设出点A,B,C,D的坐标,再由距离公式完成证明.也可以运用向量的线性运算以及数量积运算加以证明.探究一探究二探究三思维辨析证法一(解析法)
以A为坐标原点O,AB所在的直线为x轴,建立平面直角坐标系xOy,则A(0,0).
设B(a,0),C(b,c),则AC的中点E ,由对称性知D(b-a,c),
所以|AB|2=a2,|AD|2=(b-a)2+c2,
|AC|2=b2+c2,|BD|2=(b-2a)2+c2,
|AC|2+|BD|2=4a2+2b2+2c2-4ab
=2(2a2+b2+c2-2ab),
|AB|2+|AD|2=2a2+b2+c2-2ab,
所以|AC|2+|BD|2=2(|AB|2+|AD|2).探究一探究二探究三思维辨析证法二(向量法) 反思感悟建立平面直角坐标系的原则
1.如果图形有对称中心,那么可以选对称中心为原点.
2.如果图形有对称轴,那么可以选对称轴为坐标轴.
3.使图形上的特殊点尽可能多地在坐标轴上.探究一探究二探究三思维辨析变式训练1 在△ABC中,|AB|=|AC|,BD,CE分别为两腰上的高.求证:|BD|=|CE|.
证明:如图,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系.
设B(-a,0),C(a,0),A(0,h).探究一探究二探究三思维辨析求轨迹方程?
【例2】 设点A是单位圆x2+y2=1上的任意一点,l是过点A与x轴垂直的直线,点D是直线l与x轴的交点,点M在直线l上,且满足|DM|=m|DA|(m>0,且m≠1).当点A在单位圆上运动时,记点M的轨迹为曲线C.求曲线C的方程,判断曲线C为何种圆锥曲线,并求其焦点坐标.
分析:设出点M的坐标(x,y),直接利用条件求解.探究一探究二探究三思维辨析解:如图,设M(x,y),A(x0,y0),则由|DM|=m|DA|(m>0,且m≠1),可得x=x0,|y|=m|y0|,探究一探究二探究三思维辨析反思感悟求轨迹的常用方法
1.直接法:如果题目中的条件有明显的等量关系或者可以推出某个等量关系,即可用求曲线方程的五个步骤直接求解.
2.定义法:如果动点的轨迹满足某种已知曲线的定义,那么可根据定义写出轨迹方程.
3.代入法:若动点P(x,y)依赖于另一动点Q(x1,y1),而动点Q(x1,y1)又在某已知曲线上,则可先列出关于x,y,x1,y1的方程组,利用x,y表示x1,y1,把x1,y1代入已知曲线方程即为所求.
4.参数法:动点P(x,y)的横纵坐标用一个或几个参数来表示,消去参数即得其轨迹方程.探究一探究二探究三思维辨析变式训练2 在△ABC中,若BC的长度为4,中线AD的长度为3,求点A的轨迹方程.?解:取B,C所在直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系,则D(0,0),B(-2,0),C(2,0).
∴点A的轨迹方程为x2+y2=9(y≠0).探究一探究二探究三思维辨析利用坐标系解决实际问题?
【例3】 由甲导弹驱逐舰、乙导弹驱逐舰、丙综合补给舰组成的护航编队奔赴某海域执行护航任务,对商船进行护航.某日甲舰在乙舰正东6 km处,丙舰在乙舰北偏西30°,两舰相距4 km.某时刻甲舰发现商船的某种求救信号.由于乙、丙两舰比甲舰距离商船远,因此4 s后乙、丙两舰才同时发现这一信号,此信号的传播速度为1 km/s.若甲舰赶赴救援,则行进的方位角应是多少?
分析:本题求解的关键在于确定商船相对于甲舰的相对位置,因此不妨用点A,B,C表示甲舰、乙舰、丙舰,建立适当的坐标系,求出商船与甲舰的坐标,解决问题.探究一探究二探究三思维辨析解:设点A,B,C,P分别表示甲舰、乙舰、丙舰和商船.如图所示,以AB所在直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系,则A(3,0),B(-3,0),C(-5,2 ).
由题意得|PB|=|PC|,
则点P在线段BC的垂直平分线上.探究一探究二探究三思维辨析反思感悟1.由于点A,B,C的相对位置一定,解决问题的关键是如何建系,将几何位置量化,根据直线与双曲线方程求解.
2.运用坐标法解决实际问题的步骤:建系→设点→列关系式→求解数学结果→回答实际问题.探究一探究二探究三思维辨析变式训练3 已知某荒漠上有两个定点A,B,它们相距2 km,现准备在荒漠上开垦一片以AB为一条对角线的平行四边形区域建成农艺园,按照规划,围墙总长为8 km.?
(1)问:农艺园的最大面积能达到多少?
(2)该荒漠上有一条水沟l恰好经过点A,且与AB成30°的角,现要对整条水沟进行加固改造,但考虑到今后农艺园的水沟要重新改造,所以对水沟可能被农艺园围进的部分暂不加固,问:暂不加固的部分有多长?探究一探究二探究三思维辨析解:(1)设平行四边形的另两个顶点为C,D,由围墙总长为8 km,得|CA|+|CB|=4(km)>|AB|=2(km),由椭圆的定义知,点C的轨迹是以点A,B为焦点,长轴长2a=4,焦距2c=2的椭圆(去除落在直线AB上的两点).
若以AB所在直线为x轴,线段AB的垂直平分线为y轴,建立平面直角坐标系,易知点D也在此椭圆上,要使平行四边形ACBD的面积最大,则C,D为此椭圆短轴的端点,此时,面积S=2 (km2).探究一探究二探究三思维辨析探究一探究二探究三思维辨析因忽视曲线方程的意义而致误
典例已知两定点A,B,且|AB|=4,动点M满足:直线MA与MB斜率之积为常数- ,求点M的轨迹方程,并注明轨迹是什么曲线.探究一探究二探究三思维辨析正解:以AB所在直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系xOy,纠错心得1.在解本题时没有考虑到式子的意义,在 中x+2≠0,x-2≠0,即x≠±2,没有去掉相应的两个点.
2.在利用平面直角坐标系求轨迹问题时,往往会遇到去点或去掉图形的某一部分的情况,做这种题时要认真分析题目条件,求出准确的轨迹方程.探究一探究二探究三思维辨析变式训练 已知一条直线l和它上方的一个点A,点A到直线l的距离是2,一条曲线也在直线l的上方,它上面的每一点到A的距离减去到直线l的距离的差都是2,建立适当的坐标系,求这条曲线的方程.?解:取直线l为x轴,过点A且垂直于直线l的直线为y轴,建立坐标系xOy,
设点M(x,y)是曲线上任意一点,作MB⊥x轴,垂足是点B.
∵曲线在x轴的上方,∴y>0.
根据题意得|MA|-|MB|=2,1 2 3 41.已知曲线C的方程为y=x(1≤x≤5),则下列四点在曲线C上的是( )答案:D 1 2 3 42.动点P到直线x+y-4=0的距离等于它到点M(2,2)的距离,则点P的轨迹是( )
A.直线 B.椭圆
C.双曲线 D.抛物线
解析:由于点M(2,2)在直线x+y-4=0上,而|PM|等于点P到直线x+y-4=0的距离,所以动点P的轨迹是过点M且垂直于直线x+y-4=0的直线.
答案:A1 2 3 43.已知△ABC的三边a,b,c满足b2+c2=5a2,BE,CF分别为边AC,AB上的中线,则BE与CF的位置关系是 .?答案:垂直 1 2 3 44.已知△ABC的三个顶点A(-3,4),B(3,-4),C(1,7),则△ABC的形状是 .?答案:直角三角形
同课章节目录
