高中数学北师大版选修4-5课件:2.3.1 数学归纳法 :30张PPT
文档属性
| 名称 | 高中数学北师大版选修4-5课件:2.3.1 数学归纳法 :30张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 642.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 00:00:00 | ||
图片预览











文档简介
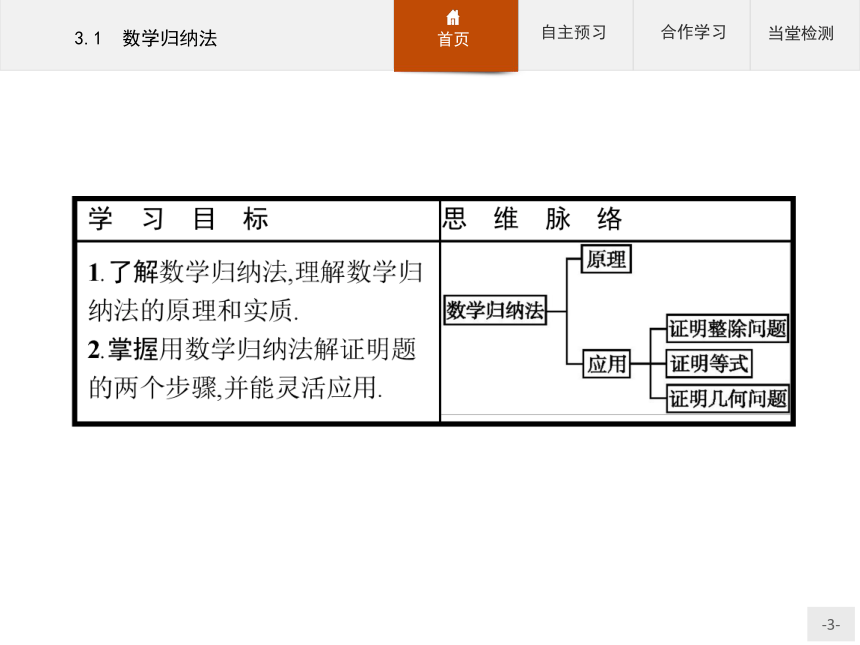
课件30张PPT。§3 数学归纳法与贝努利不等式3.1 数学归纳法对数学归纳法的理解
(1)数学归纳法原理:
数学归纳法原理是设有一个关于正整数n的命题,若当n取第1个值n0时该命题成立,又在假设当n取第k个值时该命题成立后可以推出n取第k+1个值时该命题成立,则该命题对一切自然数n≥n0都成立.
(2)数学归纳法:
数学归纳法可以用于证明与正整数有关的命题.证明需要经过两个步骤:
①验证当n取第一个值n0(如n0=1或2等)时命题正确.
②假设当n=k时(k∈N+,k≥n0)命题正确,证明当n=k+1时命题也正确.在完成了上述两个步骤之后,就可以断定命题对于从n0开始的所有正整数都正确.名师点拨 数学归纳法一般被使用证明某些涉及正整数n的命题,n可取无限多个值,但不能简单地说所有涉及正整数n的命题都可以用数学归纳法证明,例如用数学归纳法证明 的单调性就难以实现,一般来说,从n=k到n=k+1时,如果问题中存在可利用的递推关系,则数学归纳法有用武之地,否则使用数学归纳法就有困难.
在运用数学归纳法时,要注意起点n0并非一定取1,也可能取0,2等值,要看清题目,比如证明凸n边形的内角和f(n)=(n-2)×180°,这里面的n应不小于3,即n≥3,第一个值n0=3.
归纳假设的利用是数学归纳法证明的关键,这也是能否由“n=k”递推到“n=k+1”的关键,在证明过程中,需根据命题的变化或者在步骤的变化中,从数学式子的结构特点上,利用拼凑的方法,凑假设,凑结论,从而使“递推关系”得以顺利进行,命题得以证明.答案:D 答案:D 思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)用数学归纳法证明问题时,第一步是验证当n=1时结论成立.( )
(2)所有与正整数有关的数学命题都可以用数学归纳法证明.( )
(3)用数学归纳法证明问题时,只要推理过程正确,归纳假设可以不用.( )
答案:(1)× (2)× (3)×探究一探究二探究三思维辨析 分析按照数学归纳法的步骤进行证明,注意第二步中合理运用归纳假设.探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟 利用数学归纳法证明等式时应注意的问题
(1)第一步的验证,对于有些问题验证的并不是n=1,有时需验证n=2,n=3,甚至需要验证n=10,如证明:对足够大的正整数n,有2n>n3,就需要验证n=10时不等式成立.
(2)注意当n=k+1时式子的项数,特别是寻找n=k与n=k+1的式子之间的关系时,项数发生什么变化容易被弄错,因此对n=k与n=k+1时式子的正确分析是应用数学归纳法成功证明问题的保障.
(3)在第二步的证明过程中一定要用上归纳假设,否则这样的证明就不再是数学归纳法.探究一探究二探究三思维辨析变式训练1用数学归纳法证明:1+3×2+5×22+…+(2n-1)×2n-1=2n(2n-3)+3(n∈N+).
证明(1)当n=1时,左边=1,右边=2(2-3)+3=1,左边=右边,所以等式成立.
(2)假设当n=k(k∈N+)时,等式成立,即1+3×2+5×22+…+(2k-1)×2k-1=2k(2k-3)+3.
则当n=k+1时,1+3×2+5×22+…+(2k-1)×2k-1+(2k+1)×2k=2k(2k-3)+3+(2k+1)×2k=2k(4k-2)+3=2k+1[2(k+1)-3]+3,即当n=k+1时,等式也成立.
由(1)(2)知,等式对任何n∈N+都成立.探究一探究二探究三思维辨析【例2】 用数学归纳法证明:(3n+1)·7n-1(n∈N+)能被9整除.
分析在第二步证明中,注意利用归纳假设,对n=k+1时的式子进行合理变形.
证明(1)当n=1时,(3×1+1)·7-1=27能被9整除,命题成立.
(2)假设当n=k(k∈N+,k≥1)时命题成立,即(3k+1)·7k-1能被9整除.
则当n=k+1时,[3(k+1)+1]·7k+1-1=(3k+1)·7k+1-1+3·7k+1=(3k+1)·7k-1+6(3k+1)·7k+3·7k+1=(3k+1)·7k-1+9·(2k+3)·7k.
因为(3k+1)·7k-1和9·(2k+3)·7k都能被9整除,所以(3k+1)·7k-1+9·(2k+3)·7k能被9整除,即当n=k+1时,命题也成立,综合(1)(2)可知,(3n+1)·7n-1(n∈N+)能被9整除.探究一探究二探究三思维辨析反思感悟 用数学归纳法证明整除问题时,首先从要证的式子中拼凑出假设成立的式子,然后证明剩余的式子也能被某式(数)整除.其中的关键是“凑项”,可采用增项、减项、拆项和因式分解等方法分析出因子,从而利用归纳假设使问题得到解决.探究一探究二探究三思维辨析变式训练2用数学归纳法证明:an+1+(a+1)2n-1能被a2+a+1整除,其中n∈N+,a∈R.
证明(1)当n=1时,an+1+(a+1)2n-1即为a2+a+1,能够被a2+a+1整除,结论成立.
(2)假设当n=k(k∈N+)时,结论成立,即ak+1+(a+1)2k-1能够被a2+a+1整除,
则当n=k+1时,ak+2+(a+1)2k+1=a·ak+1+(a+1)2·(a+1)2k-1=a[ak+1+(a+1)2k-1]-a·(a+1)2k-1+(a+1)2·(a+1)2k-1=a[ak+1+(a+1)2k-1]-(a+1)2k-1·(a2+a+1).
由归纳假设知,上式能够被a2+a+1整除,即当n=k+1时,结论也成立.由(1)(2)可知,原结论对任意n∈N+都成立.探究一探究二探究三思维辨析【例3】平面内有n个圆,任意两个圆都相交于两点,任意三个圆不相交于同一点,求证:这n个圆将平面分成f(n)=n2-n+2个部分(n∈N+).
分析因为f(n)为n个圆把平面分割成的区域数,那么再有一个圆和这n个圆相交,就有2n个交点,这些交点将增加的这个圆分成2n段弧,且每一段弧又将原来的平面区域一分为二,所以增加一个圆后,平面分成的区域数增加2n个,即f(n+1)=f(n)+2n.有了上述关系,数学归纳法的第二步证明可迎刃而解.探究一探究二探究三思维辨析证明(1)当n=1时,一个圆将平面分成两个部分,且f(1)=1-1+2=2,所以当n=1时命题成立.
(2)假设当n=k(k∈N+,且k≥1)时命题成立,即k个圆把平面分成f(k)=k2-k+2个部分,则当n=k+1时,在k+1个圆中任取一个圆O,剩下的k个圆将平面分成f(k)个部分,而圆O 与k个圆有2k个交点,这2k个点将圆O分成2k段弧,每段弧将原平面一分为二,故得f(k+1)=f(k)+2k=k2-k+2+2k=(k+1)2-(k+1)+2.所以当n=k+1时,命题成立.
综合(1)(2)可知,对一切n∈N+,命题成立.
反思感悟 对于几何问题的证明,可以先从有限情形中归纳出一个变化的过程,或者说体会出是怎样变化的,然后再去证明,也可以用“递推”的方法来证明.证明的关键是寻找f(k+1)与f(k)之间的递推关系,从f(k+1)中将f(k)分离出来.探究一探究二探究三思维辨析探究一探究二探究三思维辨析又因为任何三条直线不共点,所以这k个交点不同于k条直线的交点,且k个交点也互不相同,如此k个交点把直线l分成(k+1)段,每一段把它所在的平面区域分成两部分,故新增加了(k+1)个部分.这时
即当n=k+1时,命题也成立.
由(1)(2)知,命题对任何n∈N+都成立.探究一探究二探究三思维辨析 因未用上归纳假设而致误
【典例】已知数列{an}中,a1=3,其前n项和Sn满足Sn=6-2an+1(n∈N+),计算a2,a3,a4,然后猜想出an的表达式,并用数学归纳法证明你的结论.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析纠错心得 1.本题在证明时出现了两个错误:
(2)未用归纳假设.
2.数学归纳法的两个步骤缺一不可,第一步中验证n的初始值至关重要,它是递推的基础,但n的初始值不一定是1,而是n的取值范围内的最小值.
3.第二步证明的关键是运用归纳假设.在使用归纳假设时,应分析p(k)与p(k+1)的差异与联系,利用拆、添、并、放、缩等手段,或从归纳假设出发,从p(k+1)中分离出p(k)再进行局部调整.探究一探究二探究三思维辨析123451.在用数学归纳法证明凸多边形内角和定理时,第一步应验证( )
A.n=1成立 B.n=2成立
C.n=3成立 D.n=4成立
解析:凸n边形的内角和为(n-2)π,最少边的凸n边形为三角形,所以应验证n=3时成立.
答案:C12345A.1 B.1+a+a2
C.1+a D.1+a+a2+a3
解析:因为当n=1时,an+1=a2,所以此时式子左边为1+a+a2.
答案:B 123453.用数学归纳法证明等式(n+1)(n+2)·…·(n+n)=2n·1·3·…·(2n-1)(n∈N+),由n=k到n=k+1时,等式左边的变化是( )
A.多乘了(2k+1)
B.多乘了2(2k+1)
C.多乘了(2k+1)(2k+2)
D.多乘了2(k+1)
解析:当n=k时,左边=(k+1)(k+2)…(k+k),当n=k+1时,左边=[(k+1)+1][(k+1)+2]…[(k+1)+(k+1)]=(k+2)(k+3)…(k+k)(2k+1)(2k+2)=(k+1)(k+2)…(k+k)· =(k+1)(k+2)…(k+k)·2(2k+1),所以多乘了2(2k+1).
答案:B123454.用数学归纳法证明“5n-2n能被3整除”的第二步中,当n=k+1时,为了使用归纳假设应将5k+1-2k+1变形为 .?
解析:假设当n=k(k∈N+,k≥1)时,5k-2k能被3整除,则当n=k+1时,5k+1-2k+1=5(5k-2k)+3·2k.
由假设知5k-2k能被3整除,又3·2k能被3整除,故5·(5k-2k)+3·2k能被3整除.
答案:5·(5k-2k)+3·2k12345
(1)数学归纳法原理:
数学归纳法原理是设有一个关于正整数n的命题,若当n取第1个值n0时该命题成立,又在假设当n取第k个值时该命题成立后可以推出n取第k+1个值时该命题成立,则该命题对一切自然数n≥n0都成立.
(2)数学归纳法:
数学归纳法可以用于证明与正整数有关的命题.证明需要经过两个步骤:
①验证当n取第一个值n0(如n0=1或2等)时命题正确.
②假设当n=k时(k∈N+,k≥n0)命题正确,证明当n=k+1时命题也正确.在完成了上述两个步骤之后,就可以断定命题对于从n0开始的所有正整数都正确.名师点拨 数学归纳法一般被使用证明某些涉及正整数n的命题,n可取无限多个值,但不能简单地说所有涉及正整数n的命题都可以用数学归纳法证明,例如用数学归纳法证明 的单调性就难以实现,一般来说,从n=k到n=k+1时,如果问题中存在可利用的递推关系,则数学归纳法有用武之地,否则使用数学归纳法就有困难.
在运用数学归纳法时,要注意起点n0并非一定取1,也可能取0,2等值,要看清题目,比如证明凸n边形的内角和f(n)=(n-2)×180°,这里面的n应不小于3,即n≥3,第一个值n0=3.
归纳假设的利用是数学归纳法证明的关键,这也是能否由“n=k”递推到“n=k+1”的关键,在证明过程中,需根据命题的变化或者在步骤的变化中,从数学式子的结构特点上,利用拼凑的方法,凑假设,凑结论,从而使“递推关系”得以顺利进行,命题得以证明.答案:D 答案:D 思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)用数学归纳法证明问题时,第一步是验证当n=1时结论成立.( )
(2)所有与正整数有关的数学命题都可以用数学归纳法证明.( )
(3)用数学归纳法证明问题时,只要推理过程正确,归纳假设可以不用.( )
答案:(1)× (2)× (3)×探究一探究二探究三思维辨析 分析按照数学归纳法的步骤进行证明,注意第二步中合理运用归纳假设.探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟 利用数学归纳法证明等式时应注意的问题
(1)第一步的验证,对于有些问题验证的并不是n=1,有时需验证n=2,n=3,甚至需要验证n=10,如证明:对足够大的正整数n,有2n>n3,就需要验证n=10时不等式成立.
(2)注意当n=k+1时式子的项数,特别是寻找n=k与n=k+1的式子之间的关系时,项数发生什么变化容易被弄错,因此对n=k与n=k+1时式子的正确分析是应用数学归纳法成功证明问题的保障.
(3)在第二步的证明过程中一定要用上归纳假设,否则这样的证明就不再是数学归纳法.探究一探究二探究三思维辨析变式训练1用数学归纳法证明:1+3×2+5×22+…+(2n-1)×2n-1=2n(2n-3)+3(n∈N+).
证明(1)当n=1时,左边=1,右边=2(2-3)+3=1,左边=右边,所以等式成立.
(2)假设当n=k(k∈N+)时,等式成立,即1+3×2+5×22+…+(2k-1)×2k-1=2k(2k-3)+3.
则当n=k+1时,1+3×2+5×22+…+(2k-1)×2k-1+(2k+1)×2k=2k(2k-3)+3+(2k+1)×2k=2k(4k-2)+3=2k+1[2(k+1)-3]+3,即当n=k+1时,等式也成立.
由(1)(2)知,等式对任何n∈N+都成立.探究一探究二探究三思维辨析【例2】 用数学归纳法证明:(3n+1)·7n-1(n∈N+)能被9整除.
分析在第二步证明中,注意利用归纳假设,对n=k+1时的式子进行合理变形.
证明(1)当n=1时,(3×1+1)·7-1=27能被9整除,命题成立.
(2)假设当n=k(k∈N+,k≥1)时命题成立,即(3k+1)·7k-1能被9整除.
则当n=k+1时,[3(k+1)+1]·7k+1-1=(3k+1)·7k+1-1+3·7k+1=(3k+1)·7k-1+6(3k+1)·7k+3·7k+1=(3k+1)·7k-1+9·(2k+3)·7k.
因为(3k+1)·7k-1和9·(2k+3)·7k都能被9整除,所以(3k+1)·7k-1+9·(2k+3)·7k能被9整除,即当n=k+1时,命题也成立,综合(1)(2)可知,(3n+1)·7n-1(n∈N+)能被9整除.探究一探究二探究三思维辨析反思感悟 用数学归纳法证明整除问题时,首先从要证的式子中拼凑出假设成立的式子,然后证明剩余的式子也能被某式(数)整除.其中的关键是“凑项”,可采用增项、减项、拆项和因式分解等方法分析出因子,从而利用归纳假设使问题得到解决.探究一探究二探究三思维辨析变式训练2用数学归纳法证明:an+1+(a+1)2n-1能被a2+a+1整除,其中n∈N+,a∈R.
证明(1)当n=1时,an+1+(a+1)2n-1即为a2+a+1,能够被a2+a+1整除,结论成立.
(2)假设当n=k(k∈N+)时,结论成立,即ak+1+(a+1)2k-1能够被a2+a+1整除,
则当n=k+1时,ak+2+(a+1)2k+1=a·ak+1+(a+1)2·(a+1)2k-1=a[ak+1+(a+1)2k-1]-a·(a+1)2k-1+(a+1)2·(a+1)2k-1=a[ak+1+(a+1)2k-1]-(a+1)2k-1·(a2+a+1).
由归纳假设知,上式能够被a2+a+1整除,即当n=k+1时,结论也成立.由(1)(2)可知,原结论对任意n∈N+都成立.探究一探究二探究三思维辨析【例3】平面内有n个圆,任意两个圆都相交于两点,任意三个圆不相交于同一点,求证:这n个圆将平面分成f(n)=n2-n+2个部分(n∈N+).
分析因为f(n)为n个圆把平面分割成的区域数,那么再有一个圆和这n个圆相交,就有2n个交点,这些交点将增加的这个圆分成2n段弧,且每一段弧又将原来的平面区域一分为二,所以增加一个圆后,平面分成的区域数增加2n个,即f(n+1)=f(n)+2n.有了上述关系,数学归纳法的第二步证明可迎刃而解.探究一探究二探究三思维辨析证明(1)当n=1时,一个圆将平面分成两个部分,且f(1)=1-1+2=2,所以当n=1时命题成立.
(2)假设当n=k(k∈N+,且k≥1)时命题成立,即k个圆把平面分成f(k)=k2-k+2个部分,则当n=k+1时,在k+1个圆中任取一个圆O,剩下的k个圆将平面分成f(k)个部分,而圆O 与k个圆有2k个交点,这2k个点将圆O分成2k段弧,每段弧将原平面一分为二,故得f(k+1)=f(k)+2k=k2-k+2+2k=(k+1)2-(k+1)+2.所以当n=k+1时,命题成立.
综合(1)(2)可知,对一切n∈N+,命题成立.
反思感悟 对于几何问题的证明,可以先从有限情形中归纳出一个变化的过程,或者说体会出是怎样变化的,然后再去证明,也可以用“递推”的方法来证明.证明的关键是寻找f(k+1)与f(k)之间的递推关系,从f(k+1)中将f(k)分离出来.探究一探究二探究三思维辨析探究一探究二探究三思维辨析又因为任何三条直线不共点,所以这k个交点不同于k条直线的交点,且k个交点也互不相同,如此k个交点把直线l分成(k+1)段,每一段把它所在的平面区域分成两部分,故新增加了(k+1)个部分.这时
即当n=k+1时,命题也成立.
由(1)(2)知,命题对任何n∈N+都成立.探究一探究二探究三思维辨析 因未用上归纳假设而致误
【典例】已知数列{an}中,a1=3,其前n项和Sn满足Sn=6-2an+1(n∈N+),计算a2,a3,a4,然后猜想出an的表达式,并用数学归纳法证明你的结论.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析纠错心得 1.本题在证明时出现了两个错误:
(2)未用归纳假设.
2.数学归纳法的两个步骤缺一不可,第一步中验证n的初始值至关重要,它是递推的基础,但n的初始值不一定是1,而是n的取值范围内的最小值.
3.第二步证明的关键是运用归纳假设.在使用归纳假设时,应分析p(k)与p(k+1)的差异与联系,利用拆、添、并、放、缩等手段,或从归纳假设出发,从p(k+1)中分离出p(k)再进行局部调整.探究一探究二探究三思维辨析123451.在用数学归纳法证明凸多边形内角和定理时,第一步应验证( )
A.n=1成立 B.n=2成立
C.n=3成立 D.n=4成立
解析:凸n边形的内角和为(n-2)π,最少边的凸n边形为三角形,所以应验证n=3时成立.
答案:C12345A.1 B.1+a+a2
C.1+a D.1+a+a2+a3
解析:因为当n=1时,an+1=a2,所以此时式子左边为1+a+a2.
答案:B 123453.用数学归纳法证明等式(n+1)(n+2)·…·(n+n)=2n·1·3·…·(2n-1)(n∈N+),由n=k到n=k+1时,等式左边的变化是( )
A.多乘了(2k+1)
B.多乘了2(2k+1)
C.多乘了(2k+1)(2k+2)
D.多乘了2(k+1)
解析:当n=k时,左边=(k+1)(k+2)…(k+k),当n=k+1时,左边=[(k+1)+1][(k+1)+2]…[(k+1)+(k+1)]=(k+2)(k+3)…(k+k)(2k+1)(2k+2)=(k+1)(k+2)…(k+k)· =(k+1)(k+2)…(k+k)·2(2k+1),所以多乘了2(2k+1).
答案:B123454.用数学归纳法证明“5n-2n能被3整除”的第二步中,当n=k+1时,为了使用归纳假设应将5k+1-2k+1变形为 .?
解析:假设当n=k(k∈N+,k≥1)时,5k-2k能被3整除,则当n=k+1时,5k+1-2k+1=5(5k-2k)+3·2k.
由假设知5k-2k能被3整除,又3·2k能被3整除,故5·(5k-2k)+3·2k能被3整除.
答案:5·(5k-2k)+3·2k12345
同课章节目录
