高中数学北师大版选修4-5课件:1.4.2 综合法、放缩法 :31张PPT
文档属性
| 名称 | 高中数学北师大版选修4-5课件:1.4.2 综合法、放缩法 :31张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 836.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 12:37:17 | ||
图片预览











文档简介
课件31张PPT。第2课时 综合法、放缩法1.综合法
(1)定义:利用某些已经证明过的不等式(例如算术平均数和几何平均数的定理)和不等式的性质,推导出所要证明的不等式,这种证明方法叫综合法.
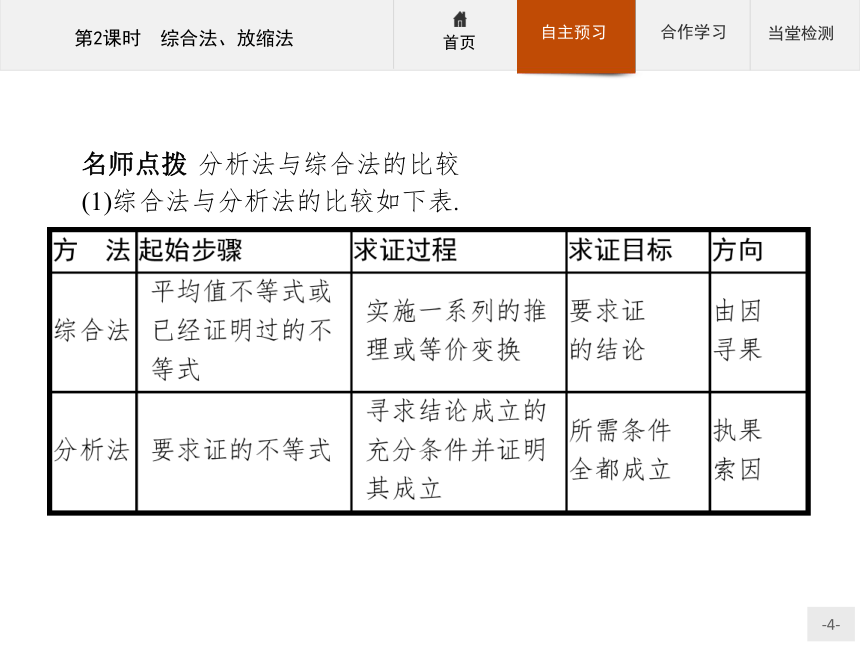
(2)证明原理:A?B1?B2?…?Bn?B,即从已知条件A出发,逐步推演不等式成立的必要条件,推导出所要证明的结论B.名师点拨 分析法与综合法的比较
(1)综合法与分析法的比较如下表.(2)用综合法与分析法证明不等式的逻辑关系.
综合法:A(已知)?B1?B2?…?Bn?B(结论)(逐步推演不等式成立的必要条件),即由条件出发推导出所要证明的不等式成立.
分析法:B(结论)?B1?B2?…?Bn?A(已知或明显成立的条件)(步步寻求不等式成立的充分条件).
总之,分析法与综合法是对立统一的两种方法.答案:A 2.放缩法
(1)定义:通过缩小(或放大)分式的分母(或分子),或通过放大(或缩小)被减式(或减式)来证明不等式,这种证明不等式的方法称为放缩法.
(2)放缩法证明不等式的主要依据:①不等式的传递性;②等量加不等量为不等量;③同分子(分母)异分母(分子)的两个分式大小的比较;④平均值不等式和绝对值不等式的性质;⑤三角函数的有界性.名师点拨 1.放缩法证明不等式常见以下四种类型:(1)直接放缩;(2)裂项放缩;(3)利用数列或函数的单调性放缩;(4)利用平均值不等式放缩.
2.用放缩法证明不等式
(1)为了证明不等式,有时需舍去或添加一些项,使不等式一边放大或缩小,利用不等式的传递性,达到证明的目的,这种方法就是放缩法.运用放缩法要注意放缩必须适当,放得过大或缩得过小都不能达到证明的目的.思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)用综合法证明不等式时,其实质是由已知逐步推演不等式成立的充分条件,从而得结论.( )
(2)若|a|<1,则|a+b|-|a-b|<2.( )
(3)综合法是直接证明,分析法是间接证明.( )
(4)有些问题的证明,可以将综合法与分析法结合起来使用.( )
答案:(1)× (2)√ (3)× (4)√探究一探究二探究三思维辨析分析欲证不等式的结构与平均值不等式有关,可考虑利用平均值不等式进行证明.探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟 利用综合法证明不等式,揭示出条件和结论之间的因果联系,要注重分析已知与求证之间、不等式的左右两端之间的差异与联系,合理进行转换,恰当选择已知不等式,这是证明的关键.探究一探究二探究三思维辨析证明因为a>0,b>0,a2+b2≥2ab,所以(a2+b2)(a+b)≥2ab(a+b),即a3+b3+a2b+ab2≥2a2b+2ab2,
所以a3+b3≥a2b+ab2.
同理可得b3+c3≥b2c+bc2,a3+c3≥a2c+ac2,
将以上三式两边分别相加,得2(a3+b3+c3)≥a2b+ab2+b2c+bc2+a2c+ac2,
所以3(a3+b3+c3)≥(a3+a2b+a2c)+(b3+ab2+b2c)+(c3+bc2+ac2)=(a+b+c)(a2+b2+c2),
所以a3+b3+c3≥ (a2+b2+c2)(a+b+c),当且仅当a=b=c时,等号成立.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟 利用放缩法证明不等式的方法与技巧
(1)利用放缩法证明不等式,要根据不等式两端的特点及已知条件,审慎地采取措施,进行恰当地放缩,任何不适宜的放缩都会导致推证的失败.
(2)一定要熟悉放缩法的具体措施及操作方法,利用放缩法证明不等式,就是采取舍掉式中一些正项或负项,或者在分式中放大或缩小分子、分母,或者把和式中各项或某项换以较大或较小的数,从而达到证明不等式的目的.探究一探究二探究三思维辨析探究一探究二探究三思维辨析分析解答本题可先采用分析法将所要证明的不等式转化为较易证明的不等式,再用综合法证明.探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟 分析法与综合法互为前提,相互渗透,分析法的终点是综合法的起点,综合法的终点又成为进一步分析法的起点,分析法和综合法要结合起来使用,也就是“两头凑”,会使问题较易解决.即在分析过程中有时进行到一定步骤不易进行下去,就要从已知条件出发,进行推理,直至综合法推出的结论与分析法追溯的充分条件统一为止,从而证明了不等式.这种“由两头往中间靠”的方法可称为分析综合法.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析纠错心得 利用放缩法证明不等式的关键是对欲证不等式中的部分项进行放大或缩小,并使放大或缩小后的项能够结合数列或其他求和知识进行化简,从而证得不等式,如果放缩不当,无法对放缩后的式子化简,就会导致错误,本题错误即在于此.探究一探究二探究三思维辨析12345A.分析法
B.综合法
C.综合法、分析法综合使用
D.间接证明法
解析:证明过程是由左到右,顺推证法,是综合法.
答案:B12345答案:B 12345答案:A<2 12345答案:(-∞,4] 12345
(1)定义:利用某些已经证明过的不等式(例如算术平均数和几何平均数的定理)和不等式的性质,推导出所要证明的不等式,这种证明方法叫综合法.
(2)证明原理:A?B1?B2?…?Bn?B,即从已知条件A出发,逐步推演不等式成立的必要条件,推导出所要证明的结论B.名师点拨 分析法与综合法的比较
(1)综合法与分析法的比较如下表.(2)用综合法与分析法证明不等式的逻辑关系.
综合法:A(已知)?B1?B2?…?Bn?B(结论)(逐步推演不等式成立的必要条件),即由条件出发推导出所要证明的不等式成立.
分析法:B(结论)?B1?B2?…?Bn?A(已知或明显成立的条件)(步步寻求不等式成立的充分条件).
总之,分析法与综合法是对立统一的两种方法.答案:A 2.放缩法
(1)定义:通过缩小(或放大)分式的分母(或分子),或通过放大(或缩小)被减式(或减式)来证明不等式,这种证明不等式的方法称为放缩法.
(2)放缩法证明不等式的主要依据:①不等式的传递性;②等量加不等量为不等量;③同分子(分母)异分母(分子)的两个分式大小的比较;④平均值不等式和绝对值不等式的性质;⑤三角函数的有界性.名师点拨 1.放缩法证明不等式常见以下四种类型:(1)直接放缩;(2)裂项放缩;(3)利用数列或函数的单调性放缩;(4)利用平均值不等式放缩.
2.用放缩法证明不等式
(1)为了证明不等式,有时需舍去或添加一些项,使不等式一边放大或缩小,利用不等式的传递性,达到证明的目的,这种方法就是放缩法.运用放缩法要注意放缩必须适当,放得过大或缩得过小都不能达到证明的目的.思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)用综合法证明不等式时,其实质是由已知逐步推演不等式成立的充分条件,从而得结论.( )
(2)若|a|<1,则|a+b|-|a-b|<2.( )
(3)综合法是直接证明,分析法是间接证明.( )
(4)有些问题的证明,可以将综合法与分析法结合起来使用.( )
答案:(1)× (2)√ (3)× (4)√探究一探究二探究三思维辨析分析欲证不等式的结构与平均值不等式有关,可考虑利用平均值不等式进行证明.探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟 利用综合法证明不等式,揭示出条件和结论之间的因果联系,要注重分析已知与求证之间、不等式的左右两端之间的差异与联系,合理进行转换,恰当选择已知不等式,这是证明的关键.探究一探究二探究三思维辨析证明因为a>0,b>0,a2+b2≥2ab,所以(a2+b2)(a+b)≥2ab(a+b),即a3+b3+a2b+ab2≥2a2b+2ab2,
所以a3+b3≥a2b+ab2.
同理可得b3+c3≥b2c+bc2,a3+c3≥a2c+ac2,
将以上三式两边分别相加,得2(a3+b3+c3)≥a2b+ab2+b2c+bc2+a2c+ac2,
所以3(a3+b3+c3)≥(a3+a2b+a2c)+(b3+ab2+b2c)+(c3+bc2+ac2)=(a+b+c)(a2+b2+c2),
所以a3+b3+c3≥ (a2+b2+c2)(a+b+c),当且仅当a=b=c时,等号成立.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟 利用放缩法证明不等式的方法与技巧
(1)利用放缩法证明不等式,要根据不等式两端的特点及已知条件,审慎地采取措施,进行恰当地放缩,任何不适宜的放缩都会导致推证的失败.
(2)一定要熟悉放缩法的具体措施及操作方法,利用放缩法证明不等式,就是采取舍掉式中一些正项或负项,或者在分式中放大或缩小分子、分母,或者把和式中各项或某项换以较大或较小的数,从而达到证明不等式的目的.探究一探究二探究三思维辨析探究一探究二探究三思维辨析分析解答本题可先采用分析法将所要证明的不等式转化为较易证明的不等式,再用综合法证明.探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟 分析法与综合法互为前提,相互渗透,分析法的终点是综合法的起点,综合法的终点又成为进一步分析法的起点,分析法和综合法要结合起来使用,也就是“两头凑”,会使问题较易解决.即在分析过程中有时进行到一定步骤不易进行下去,就要从已知条件出发,进行推理,直至综合法推出的结论与分析法追溯的充分条件统一为止,从而证明了不等式.这种“由两头往中间靠”的方法可称为分析综合法.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析纠错心得 利用放缩法证明不等式的关键是对欲证不等式中的部分项进行放大或缩小,并使放大或缩小后的项能够结合数列或其他求和知识进行化简,从而证得不等式,如果放缩不当,无法对放缩后的式子化简,就会导致错误,本题错误即在于此.探究一探究二探究三思维辨析12345A.分析法
B.综合法
C.综合法、分析法综合使用
D.间接证明法
解析:证明过程是由左到右,顺推证法,是综合法.
答案:B12345答案:B 12345答案:A<2 12345答案:(-∞,4] 12345
同课章节目录
