高中数学人教A版选修4-1课件:1.2 平行线分线段成比例定理 :28张PPT
文档属性
| 名称 | 高中数学人教A版选修4-1课件:1.2 平行线分线段成比例定理 :28张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 00:00:00 | ||
图片预览





文档简介
课件28张PPT。二 平行线分线段成比例定理121.平行线分线段成比例定理
(1)定理:三条平行线截两条直线,所得的对应线段成比例.
(2)符号表示:如图所示,1212122.推论
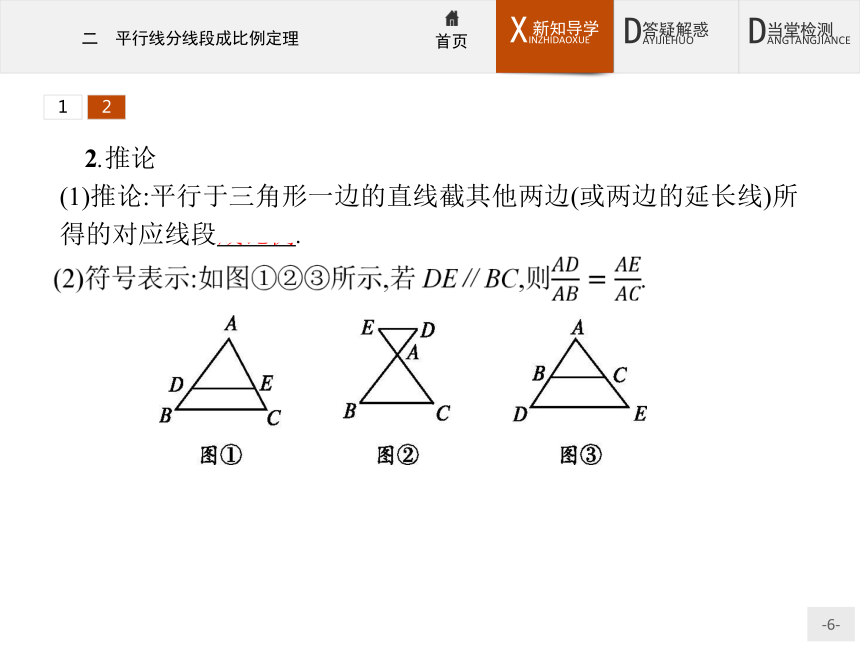
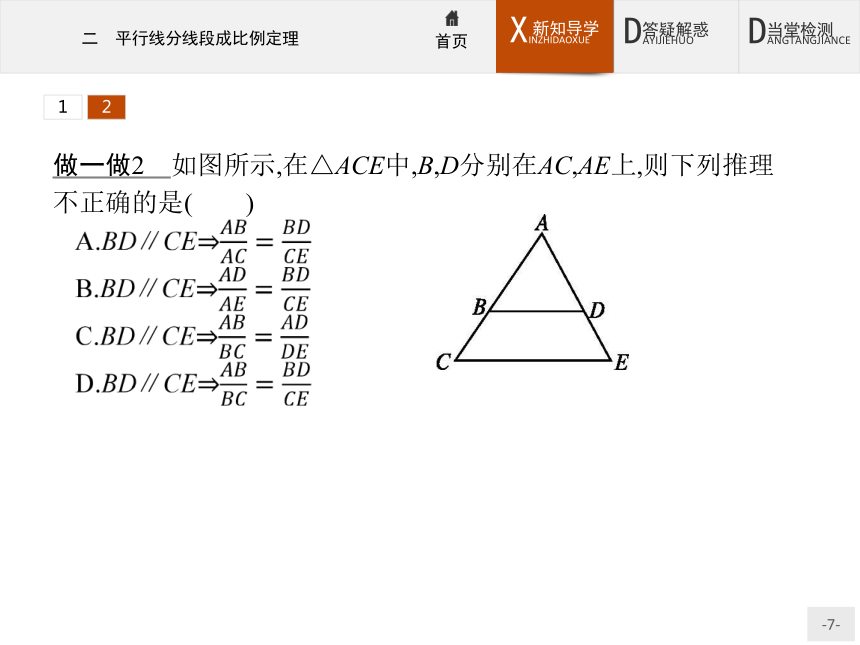
(1)推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.12做一做2 如图所示,在△ACE中,B,D分别在AC,AE上,则下列推理不正确的是( )?
解析由平行线分线段成比例定理的推论不难得出A,B,C都是正确的,D是错误的.
答案D12思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)三条平行线只有截两条平行线,所得的线段才成比例.( )
(2)平行于三角形一边的直线截其他两边所得的对应线段可能相等. ( )
(3)在△ABC中,若直线MN与BC平行,且分别与AB,AC相交于
(4)平行于梯形两底的直线截两腰所得的对应线段成比例.( )
答案(1)× (2)√ (3)× (4)√探究一探究二探究三思维辨析探究一证明线段成比例?
【例1】如图所示,已知直线FD与△ABC的BC边交于点D,与AC边交于点E,与BA的延长线交于点F,且BD=DC.求证:AE·FB=EC·FA.
分析过点A作BC的平行线,构造平行线组,然后再利用平行线分线段成比例定理得到成比例的线段,最后转化为欲证线段乘积之间的关系.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究二证明线段相等?
【例2】 如图,在△ABC中,E为中线AD上的一点, ,连接BE并延长,交AC于点F,求证:AF=CF.
分析过点D作AC的平行线,由平行线分线段成比例定理构造成比例线段进行证明.探究一探究二探究三思维辨析证明
过点D作DH∥AC,交BF于点H,如图所示.
∵D是BC的中点,探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究三求线段的长度及其比值?
【例3】 如图,在△ABC中,DE∥BC,EF∥CD,若BC=3,DE=2,DF=1,求AB的长度.
分析根据已知条件中的两组平行线得到线段比值相等,再结合已知线段长度求出AB的长度.探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练3?如图,将一块边长为12的正方形纸ABCD的顶点A折叠至边CD上的点E,使DE=5,折痕为PQ,求 的值.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析123451.如图,l1∥l2∥l3,已知AB=6 cm,BC=3 cm,A1B1=4 cm,则B1C1的长为( )
A.6 cm B.4 cm
C.3 cm D.2 cm12345123451234512345
(1)定理:三条平行线截两条直线,所得的对应线段成比例.
(2)符号表示:如图所示,1212122.推论
(1)推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.12做一做2 如图所示,在△ACE中,B,D分别在AC,AE上,则下列推理不正确的是( )?
解析由平行线分线段成比例定理的推论不难得出A,B,C都是正确的,D是错误的.
答案D12思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)三条平行线只有截两条平行线,所得的线段才成比例.( )
(2)平行于三角形一边的直线截其他两边所得的对应线段可能相等. ( )
(3)在△ABC中,若直线MN与BC平行,且分别与AB,AC相交于
(4)平行于梯形两底的直线截两腰所得的对应线段成比例.( )
答案(1)× (2)√ (3)× (4)√探究一探究二探究三思维辨析探究一证明线段成比例?
【例1】如图所示,已知直线FD与△ABC的BC边交于点D,与AC边交于点E,与BA的延长线交于点F,且BD=DC.求证:AE·FB=EC·FA.
分析过点A作BC的平行线,构造平行线组,然后再利用平行线分线段成比例定理得到成比例的线段,最后转化为欲证线段乘积之间的关系.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究二证明线段相等?
【例2】 如图,在△ABC中,E为中线AD上的一点, ,连接BE并延长,交AC于点F,求证:AF=CF.
分析过点D作AC的平行线,由平行线分线段成比例定理构造成比例线段进行证明.探究一探究二探究三思维辨析证明
过点D作DH∥AC,交BF于点H,如图所示.
∵D是BC的中点,探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究三求线段的长度及其比值?
【例3】 如图,在△ABC中,DE∥BC,EF∥CD,若BC=3,DE=2,DF=1,求AB的长度.
分析根据已知条件中的两组平行线得到线段比值相等,再结合已知线段长度求出AB的长度.探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练3?如图,将一块边长为12的正方形纸ABCD的顶点A折叠至边CD上的点E,使DE=5,折痕为PQ,求 的值.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析123451.如图,l1∥l2∥l3,已知AB=6 cm,BC=3 cm,A1B1=4 cm,则B1C1的长为( )
A.6 cm B.4 cm
C.3 cm D.2 cm12345123451234512345
