高中数学人教A版选修4-1课件:2.1 圆周角定理 :35张PPT
文档属性
| 名称 | 高中数学人教A版选修4-1课件:2.1 圆周角定理 :35张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 00:00:00 | ||
图片预览








文档简介
课件35张PPT。第二讲 直线与圆的位置关系
一 圆周角定理1231.圆周角定理
(1)圆周角定义:顶点在圆上,并且两边和圆相交的角叫做圆周角.
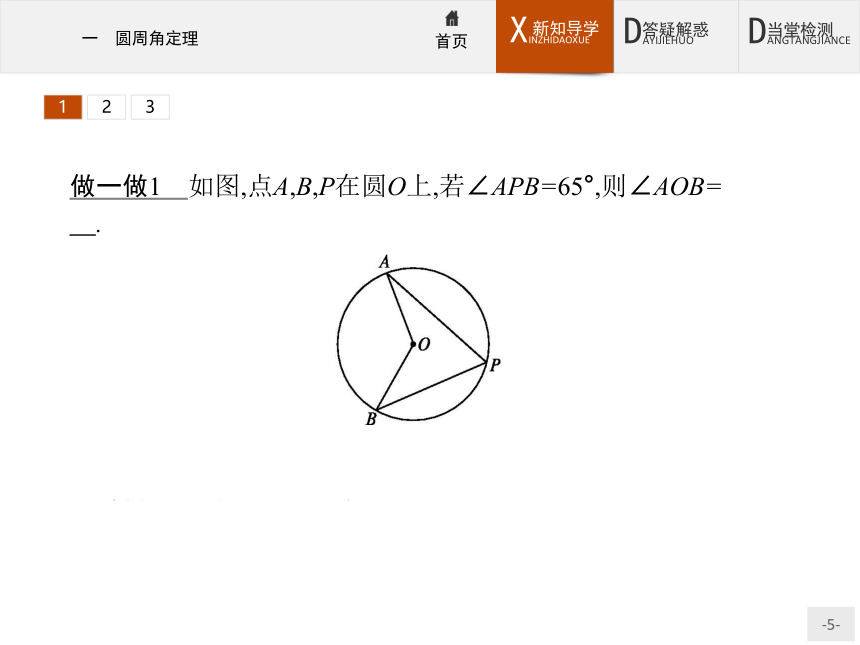
(2)圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半.123做一做1 如图,点A,B,P在圆O上,若∠APB=65°,则∠AOB= .?
解析由圆周角定理可得∠AOB=2∠APB=130°.
答案130°1232.圆心角定理
(1)圆心角定义:顶点在圆心的角叫做圆心角.
(2)圆心角定理:圆心角的度数等于它所对弧的度数.123做一做2 如图是两个同心圆,圆心为点O,点C,D在大圆上,A,B,M在小圆上,若∠AMB=40°,则劣弧 的度数等于( )?
A.20° B.40° C.80° D.70°
解析因为∠AMB=40°,所以∠AOB=80°,从而劣弧 的度数为80°.
答案C1233.圆周角定理的推论
(1)推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.
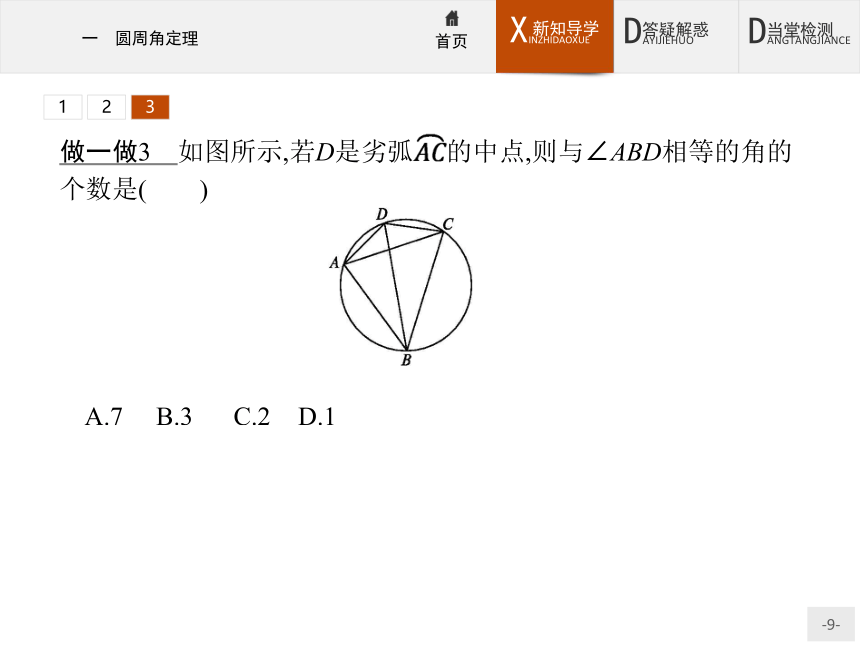
(2)推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.123做一做3 如图所示,若D是劣弧 的中点,则与∠ABD相等的角的个数是( )?
A.7 B.3 C.2 D.1
解析由同弧或等弧所对的圆周角相等,知∠ABD=∠CBD=∠ACD=∠DAC,故与∠ABD相等的角有3个.
答案B123思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)在同圆或等圆中,圆周角等于圆心角的一半. ( )
(2)在同圆或等圆中,圆心角等于它所对的弧. ( )
(3)同弦或等弦所对的圆周角相等. ( )
(4)在同圆或等圆中,相等的圆周角所对的弦也相等. ( )
答案(1)× (2)× (3)× (4)√探究一探究二探究三思维辨析探究一角、弦、弧等的计算问题?
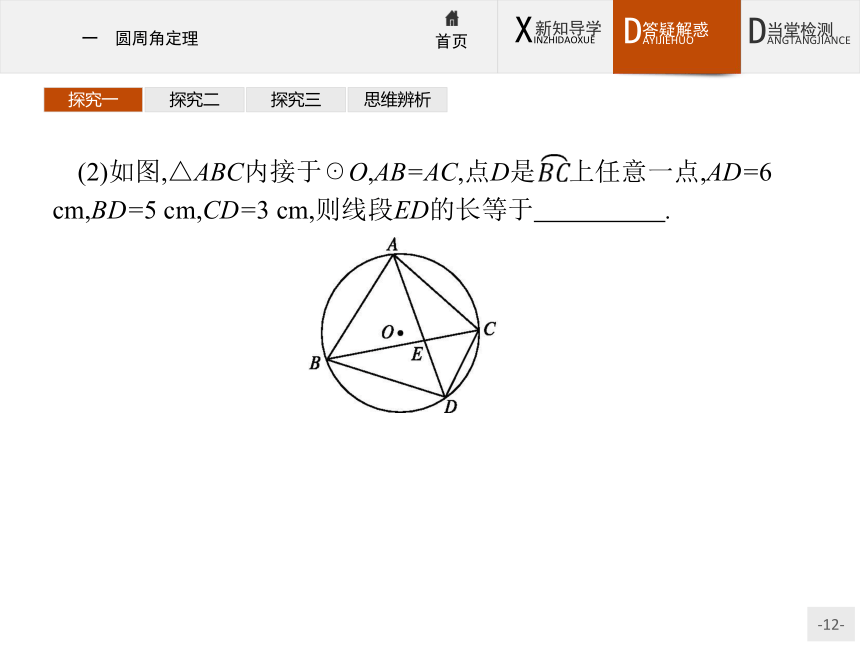
【例1】 (1)如图,在?ABCD中,∠D=60°,以点A为圆心,AB的长为半径画圆分别交AD,BC于点F,G,延长BA交☉A于E,则 的度数等于 .?探究一探究二探究三思维辨析(2)如图,△ABC内接于☉O,AB=AC,点D是 上任意一点,AD=6 cm,BD=5 cm,CD=3 cm,则线段ED的长等于 .?探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练1 如图,点A,B,C是圆O上的点,且AB=4,∠ACB=30°,则圆O的面积等于( )?
A.4π B.8π C.12π D.16π
解析连接OA,OB,∵∠ACB=30°,
∴∠AOB=60°.
又OA=OB,
∴△AOB为等边三角形.
∵AB=4,∴OA=OB=4,∴S☉O=π·42=16π.
答案D探究一探究二探究三思维辨析探究二角、弦、弧关系的证明问题?
【例2】如图,AB是☉O的一条弦,∠ACB的平分线交AB于点E,交☉O于点D.求证:AC·CB=DC·CE.分析通过圆周角定理与圆心角定理证明△ACE与△DCB相似,得到比例式,再转化为等积式.探究一探究二探究三思维辨析证明连接BD,在△ACE与△DCB中,
∵∠EAC与∠BDC是同弧所对的圆周角,
∴∠EAC=∠BDC.又CE为∠ACB的平分线,探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练2 如图,在☉O中,已知AB=AC,D是BC延长线上的一点,AD交☉O于E,求证:AB2=AD·AE.?探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练3 如图所示,已知AB是半圆O的直径,弦AD,BC相交于P,若CD=3,AB=4,则tan∠BPD等于 ( )?探究一探究二探究三思维辨析探究一探究二探究三思维辨析错用圆周角定理致误
典例已知☉O中的弦AB的长等于半径,求弦AB所对的圆心角和圆周角的度数.
错解根据题意画出大致示意图,如图所示,∠AOB和∠C分别是弦AB所对的圆心角和圆周角.∵AB=OA=OB,∴△OAB为等边三角形,
∴∠AOB=60°,∴∠C=30°,
∴弦AB所对的圆心角为60°,它所对的圆周角为30°.探究一探究二探究三思维辨析正解根据题意画出大致示意图如图所示,
∠AOB为弦AB所对的圆心角,∠C和∠D是弦AB所对的圆周角.
∵AB=OA=OB,∴△AOB为等边三角形,
∴∠AOB=60°,∴∠C=30°,∴∠D=150°,∴弦AB所对的圆心角为60°,所对的圆周角为30°或150°.探究一探究二探究三思维辨析探究一探究二探究三思维辨析123451.如图,点C,D,M在圆O上,若∠OCD=15°,则∠CMD的度数等于( )
A.30° B.150° C.75° D.60°
解析因为∠OCD=15°,
答案C123452.如图所示,在☉O中,已知∠ACB=∠CDB=60°,AC=3,则△ABC的周长等于( )
解析由圆周角定理得∠BAC=∠CDB=∠ACB=60°,所以△ABC为等边三角形,所以其周长等于9.
答案A123453.如图所示,若圆内接四边形ABCD的对角线AC,BD相交于E,则图中相似三角形有( )
A.1对 B.2对 C.3对 D.4对
解析由推论1知∠ADB=∠ACB,∠ABD=∠ACD,∠BAC=∠BDC,∠CAD=∠CBD,∴△AEB∽△DEC,△AED∽△BEC.
答案B123454.如图所示,AB为☉O的直径,AC=4 cm,BC=3 cm,CD⊥AB于D,则CD的长为 cm.?123455.如图,AB是圆O的直径,D,E为圆O上位于AB异侧的两点,连接BD并延长至点C,使BD=DC,连接AC,AE,DE.求证:∠E=∠C.12345证明如图,连接OD,
∵BD=DC,O为AB的中点,
∴OD∥AC,∴∠ODB=∠C.
∵OB=OD,∴∠ODB=∠B.∴∠B=∠C.
∵点A,E,B,D都在圆O上,且D,E为圆O上位于AB异侧的两点,
∴∠E和∠B为同弧所对的圆周角.
∴∠E=∠B,∴∠E=∠C.
(1)圆周角定义:顶点在圆上,并且两边和圆相交的角叫做圆周角.
(2)圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半.123做一做1 如图,点A,B,P在圆O上,若∠APB=65°,则∠AOB= .?
解析由圆周角定理可得∠AOB=2∠APB=130°.
答案130°1232.圆心角定理
(1)圆心角定义:顶点在圆心的角叫做圆心角.
(2)圆心角定理:圆心角的度数等于它所对弧的度数.123做一做2 如图是两个同心圆,圆心为点O,点C,D在大圆上,A,B,M在小圆上,若∠AMB=40°,则劣弧 的度数等于( )?
A.20° B.40° C.80° D.70°
解析因为∠AMB=40°,所以∠AOB=80°,从而劣弧 的度数为80°.
答案C1233.圆周角定理的推论
(1)推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.
(2)推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.123做一做3 如图所示,若D是劣弧 的中点,则与∠ABD相等的角的个数是( )?
A.7 B.3 C.2 D.1
解析由同弧或等弧所对的圆周角相等,知∠ABD=∠CBD=∠ACD=∠DAC,故与∠ABD相等的角有3个.
答案B123思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)在同圆或等圆中,圆周角等于圆心角的一半. ( )
(2)在同圆或等圆中,圆心角等于它所对的弧. ( )
(3)同弦或等弦所对的圆周角相等. ( )
(4)在同圆或等圆中,相等的圆周角所对的弦也相等. ( )
答案(1)× (2)× (3)× (4)√探究一探究二探究三思维辨析探究一角、弦、弧等的计算问题?
【例1】 (1)如图,在?ABCD中,∠D=60°,以点A为圆心,AB的长为半径画圆分别交AD,BC于点F,G,延长BA交☉A于E,则 的度数等于 .?探究一探究二探究三思维辨析(2)如图,△ABC内接于☉O,AB=AC,点D是 上任意一点,AD=6 cm,BD=5 cm,CD=3 cm,则线段ED的长等于 .?探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练1 如图,点A,B,C是圆O上的点,且AB=4,∠ACB=30°,则圆O的面积等于( )?
A.4π B.8π C.12π D.16π
解析连接OA,OB,∵∠ACB=30°,
∴∠AOB=60°.
又OA=OB,
∴△AOB为等边三角形.
∵AB=4,∴OA=OB=4,∴S☉O=π·42=16π.
答案D探究一探究二探究三思维辨析探究二角、弦、弧关系的证明问题?
【例2】如图,AB是☉O的一条弦,∠ACB的平分线交AB于点E,交☉O于点D.求证:AC·CB=DC·CE.分析通过圆周角定理与圆心角定理证明△ACE与△DCB相似,得到比例式,再转化为等积式.探究一探究二探究三思维辨析证明连接BD,在△ACE与△DCB中,
∵∠EAC与∠BDC是同弧所对的圆周角,
∴∠EAC=∠BDC.又CE为∠ACB的平分线,探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练2 如图,在☉O中,已知AB=AC,D是BC延长线上的一点,AD交☉O于E,求证:AB2=AD·AE.?探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练3 如图所示,已知AB是半圆O的直径,弦AD,BC相交于P,若CD=3,AB=4,则tan∠BPD等于 ( )?探究一探究二探究三思维辨析探究一探究二探究三思维辨析错用圆周角定理致误
典例已知☉O中的弦AB的长等于半径,求弦AB所对的圆心角和圆周角的度数.
错解根据题意画出大致示意图,如图所示,∠AOB和∠C分别是弦AB所对的圆心角和圆周角.∵AB=OA=OB,∴△OAB为等边三角形,
∴∠AOB=60°,∴∠C=30°,
∴弦AB所对的圆心角为60°,它所对的圆周角为30°.探究一探究二探究三思维辨析正解根据题意画出大致示意图如图所示,
∠AOB为弦AB所对的圆心角,∠C和∠D是弦AB所对的圆周角.
∵AB=OA=OB,∴△AOB为等边三角形,
∴∠AOB=60°,∴∠C=30°,∴∠D=150°,∴弦AB所对的圆心角为60°,所对的圆周角为30°或150°.探究一探究二探究三思维辨析探究一探究二探究三思维辨析123451.如图,点C,D,M在圆O上,若∠OCD=15°,则∠CMD的度数等于( )
A.30° B.150° C.75° D.60°
解析因为∠OCD=15°,
答案C123452.如图所示,在☉O中,已知∠ACB=∠CDB=60°,AC=3,则△ABC的周长等于( )
解析由圆周角定理得∠BAC=∠CDB=∠ACB=60°,所以△ABC为等边三角形,所以其周长等于9.
答案A123453.如图所示,若圆内接四边形ABCD的对角线AC,BD相交于E,则图中相似三角形有( )
A.1对 B.2对 C.3对 D.4对
解析由推论1知∠ADB=∠ACB,∠ABD=∠ACD,∠BAC=∠BDC,∠CAD=∠CBD,∴△AEB∽△DEC,△AED∽△BEC.
答案B123454.如图所示,AB为☉O的直径,AC=4 cm,BC=3 cm,CD⊥AB于D,则CD的长为 cm.?123455.如图,AB是圆O的直径,D,E为圆O上位于AB异侧的两点,连接BD并延长至点C,使BD=DC,连接AC,AE,DE.求证:∠E=∠C.12345证明如图,连接OD,
∵BD=DC,O为AB的中点,
∴OD∥AC,∴∠ODB=∠C.
∵OB=OD,∴∠ODB=∠B.∴∠B=∠C.
∵点A,E,B,D都在圆O上,且D,E为圆O上位于AB异侧的两点,
∴∠E和∠B为同弧所对的圆周角.
∴∠E=∠B,∴∠E=∠C.
