2019_2020学年高中数学第三章函数的应用3.2.2函数模型的应用实例教案新人教A版必修1
文档属性
| 名称 | 2019_2020学年高中数学第三章函数的应用3.2.2函数模型的应用实例教案新人教A版必修1 |  | |
| 格式 | zip | ||
| 文件大小 | 289.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 14:01:31 | ||
图片预览



文档简介
3.2.2 函数模型的应用实例
[目标] 1.会用分段函数模型或自建函数模型解决一些简单的实际问题;2.会根据所给数据选择合适的函数模型进行拟合.
[重点] 根据给定的函数模型解决实际问题.
[难点] 建立数学模型解答实际问题.
知识点一 解函数模型应用题的一般步骤
[填一填]
1.函数模型应用的两个方面
(1)利用已知函数模型解决问题;
(2)建立恰当的函数模型,并利用所得函数模型解释有关现象,对某些发展趋势进行预测.
2.解函数应用题的一般步骤
(1)审题:弄清题意,分清条件和结论,理顺数理关系.
(2)建模:将文字语言转化为数学语言,用数学知识建立相应的数学模型.
(3)求模:求解数学模型,得到数学结论.
(4)还原:将用数学方法得到的结论还原为实际问题.
[答一答]
1.常见的函数模型有哪些?
提示:(1)正比例函数模型:f(x)=kx(k为常数,k≠0);
(2)反比例函数模型:f(x)=(k为常数,k≠0);
(3)一次函数模型:f(x)=kx+b(k,b为常数,k≠0);
(4)二次函数模型:f(x)=ax2+bx+c(a,b,c为常数,a≠0);
(5)指数函数模型:f(x)=abx+c(a,b,c为常数,a≠0,b>0,b≠1);
(6)对数函数模型:f(x)=mlogax+n(m,n,a为常数,m≠0,a>0,a≠1);
(7)幂函数模型:f(x)=axn+b(a,b,n为常数,a≠0,n≠1).
知识点二 函数拟合与预测的一般步骤
[填一填]
(1)收集数据;
(2)画散点图;
(3)选择函数模型;
(4)求函数模型;
(5)检验.若符合实际情况,则用函数模型解释实际问题;若不符合实际情况则从(3)重新开始.
[答一答]
2.如何根据收集到的数据解决实际问题?
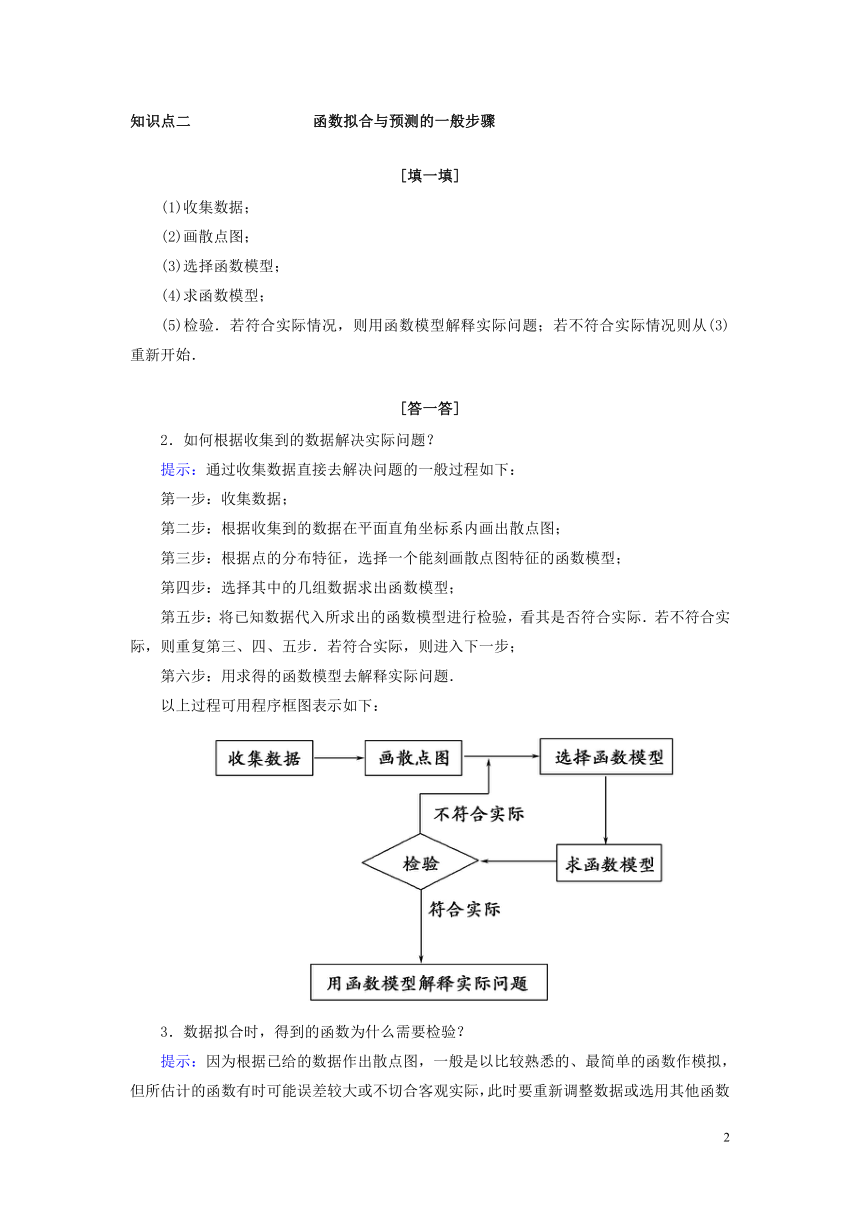
提示:通过收集数据直接去解决问题的一般过程如下:
第一步:收集数据;
第二步:根据收集到的数据在平面直角坐标系内画出散点图;
第三步:根据点的分布特征,选择一个能刻画散点图特征的函数模型;
第四步:选择其中的几组数据求出函数模型;
第五步:将已知数据代入所求出的函数模型进行检验,看其是否符合实际.若不符合实际,则重复第三、四、五步.若符合实际,则进入下一步;
第六步:用求得的函数模型去解释实际问题.
以上过程可用程序框图表示如下:
3.数据拟合时,得到的函数为什么需要检验?
提示:因为根据已给的数据作出散点图,一般是以比较熟悉的、最简单的函数作模拟,但所估计的函数有时可能误差较大或不切合客观实际,此时要重新调整数据或选用其他函数模型.
类型一 建立函数模型的应用题
[例1] 某汽车城销售某种型号的汽车,进货单价为25万元.市场调研表明:当销售单价为29万元时,平均每周能售出8辆,而当销售单价每降低0.5万元时,平均每周能多售出4辆.设每辆汽车降价x万元,每辆汽车的销售利润为y万元(每辆车的销售利润=销售单价-进货单价).
(1)求y与x之间的函数关系式,并在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的销售单价为多少万元时,平均每周的销售利润最大?最大利润是多少?
[分析] 解决本题需弄清楚:每辆车的销售利润=销售单价-进货单价;先求出每辆车的销售利润,再乘以售出辆数可得每周销售利润.通过二次函数求最值,可得汽车合适的销售单价.
[解] (1)因为y=29-25-x,
所以y=-x+4(0≤x≤4).
(2)z=(8+×4)y=(8x+8)(-x+4)=-8x2+24x+32(0≤x≤4).
(3)由(2)知,z=-8x2+24x+32=-8(x-1.5)2+50(0≤x≤4).故当x=1.5时,zmax=50.
所以当销售单价为29-1.5=27.5万元时,每周的销售利润最大,最大利润为50万元.
在函数模型中,二次函数模型占有重要的地位,因为根据实际问题建立函数解析式后,可利用配方法、判别式法、换元法、函数的单调性等来求函数的最值,从而解决实际问题中的最大、最小等问题.
[变式训练1] 据市场分析,烟台某海鲜加工公司当月产量在10吨至25吨时,月生产总成本y(万元)可以看成月产量x(吨)的二次函数;当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元,且为二次函数的顶点.
(1)写出月总成本y(万元)关于月产量x(吨)的函数关系式;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润?
解:(1)设y=a(x-15)2+17.5,
将x=10,y=20代入上式,得20=25a+17.5.
解得a=.
所以y=(x-15)2+17.5(10≤x≤25).
(2)设最大利润为Q(x),
则Q(x)=1.6x-y=1.6x-
=-(x-23)2+12.9(10≤x≤25).
因为x=23∈[10,25],
所以月产量为23吨时,可获最大利润12.9万元.
类型二 已知函数模型的应用题
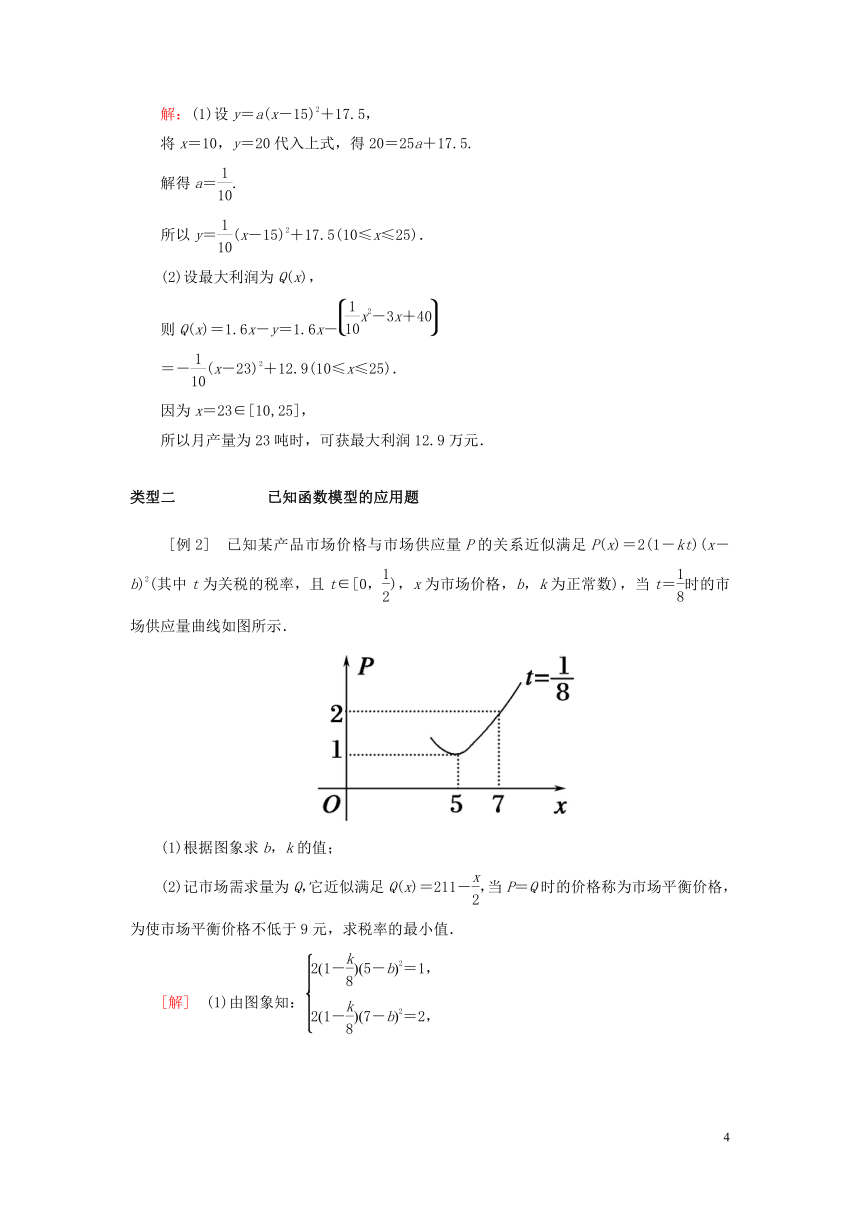
[例2] 已知某产品市场价格与市场供应量P的关系近似满足P(x)=2(1-kt)(x-b)2(其中t为关税的税率,且t∈[0,),x为市场价格,b,k为正常数),当t=时的市场供应量曲线如图所示.
(1)根据图象求b,k的值;
(2)记市场需求量为Q,它近似满足Q(x)=211-,当P=Q时的价格称为市场平衡价格,为使市场平衡价格不低于9元,求税率的最小值.
[解] (1)由图象知:
??
(2)当P=Q时,有2(1-6t)(x-5)2=211-,
即(1-6t)(x-5)2=11-
?2(1-6t)==
=-.
令m=,则2(1-6t)=17m2-m.
∵x≥9,∴m∈(0,].
当m=时,2(1-6t)取最大值,故t≥,
即税率的最小值为.
(1(本题利用已知函数模型解决实际问题,首先利用给出的函数图象,通过待定系数法确定函数关系式,再利用函数关系式求最值,求最值时注意自变量的取值范围.
(2(对于题中已给出数学模型问题,只要解数学模型即可,较常用的方法是待定系数法解模型,然后利用相应的解析式及对应函数的性质解决实际问题.
[变式训练2] 灌满开水的热水瓶放在室内,如果瓶内开水原来的温度是θ1度,室内气温是θ0度,t分钟后,开水的温度可由公式θ=θ0+(θ1-θ0)e-kt求得,这里,k是一个与热水瓶类型有关的正的常量.现有一只某种类型的热水瓶,测得瓶内水温为100℃,过1小时后又测得瓶内水温变为98℃.已知某种奶粉必须用不低于85℃的开水冲调,现用这种类型的热水瓶在早上六点灌满100℃的开水,问:能否在这一天的中午十二点用这瓶开水来冲调上述奶粉?(假定该地白天室温为20℃)
解:根据题意,有98=20+(100-20)e-60k,
整理得e-60k=.
利用计算器,解得k=0.000 422 2.
故θ=20+80e-0.000 422 2t.
从早上六点至中午十二点共过去6小时,即360分钟.
当t=360时,θ=20+80e-0.000 422 2×360=20+80e-0.152,
由计算器算得θ≈88℃>85℃,
即能够在这一天的中午十二点用这瓶开水来冲调奶粉.
类型三 拟合函数模型的应用题
[例3] 某个体经营者把开始六个月试销A,B两种商品的逐月投资与所获纯利润列成下表:
该经营者准备下月投入12万元经营这两种产品,但不知投入A,B两种商品各多少万元才合算.请你帮助制定一个资金投入方案,使得该经营者能获得最大利润,并按你的方案求出该经营者下月可获得的最大纯利润(结果保留两个有效数字).
[分析] 只给出数据,没明确函数关系,这样就需要准确的画出散点图.然后根据图形选择合适的函数模型来解决实际问题.
[解] 以投资额为横坐标,纯利润为纵坐标,在平面直角坐标系中画出散点图,如图所示.
观察散点图可以看出,A种商品的所获纯利润y与投资额x之间的变化规律可以用二次函数模型进行模拟,如图①所示.
取(4,2)为最高点,则y=a(x-4)2+2,再把点(1,0.65)代入,得0.65=a(1-4)2+2,解得a=-0.15,所以y=-0.15(x-4)2+2.
B种商品所获纯利润y与投资额x之间的变化规律是线性的,可以用一次函数模型进行模拟,如图②所示.
设y=kx+b,取点(1,0.25)和(4,1)代入,
得解得所以y=0.25x.
即前六个月所获纯利润y关于月投资A种商品的金额x的函数关系式是y=-0.15(x-4)2+2;前六个月所获纯利润y关于月投资B种商品的金额x的函数关系式是y=0.25x.
设下月投入A,B两种商品的资金分别为xA,xB(万元),总利润为W(万元),
那么
所以W=-0.15(xA-)2+0.15×()2+2.6.
当xA=≈3.2(万元)时,W取最大值,约为4.1万元,此时xB≈8.8(万元).
即该经营者下月把12万元中的3.2万元投资A种商品,8.8万元投资B种商品,可获得最大利润约为4.1万元.
拟合数据,建立函数模型解决实际问题的一般步骤:根据收集到的数据作出散点图,然后根据散点图的形状,选用比较接近的可能的函数模型来描述所涉及的数量之间的关系,然后利用待定系数法确定出具体的函数解析式,若符合实际,可用此函数模型解释问题,若不符合实际,则继续选择模型,重复操作过程.
[变式训练3] 我国2014年至2017年国内生产总值(单位:万亿元)如下表所示:
年份
2014
2015
2016
2017
x
0
1
2
3
生产总值y
8.206 7
8.944 2
9.593 3
10.239 8
(1)画出函数图象,猜想它们之间的函数关系,近似地写出一个函数关系式;
(2)利用得出的关系式求生产总值,与表中实际生产总值比较.
解:
(1)画出函数图象,如图所示,从函数的图象可以看出,画出的点近似地落在一条直线上,设所求的一次函数为y=kx+b(k≠0).
把点(0,8.206 7)和(3,10.239 8)的坐标代入上式,解方程组,得
因此所求的函数关系式为y=0.677 7x+8.206 7.
(2)由得到的关系式计算出2015年和2016年的国内生产总值分别为0.677 7×1+8.206 7=8.884 4(万亿元),
0.677 7×2+8.206 7=9.562 1(万亿元).
与实际的生产总值相比,误差不超过0.1万亿元.
1.一根蜡烛长20 cm,点燃后每小时燃烧5 cm,燃烧时剩下的高度h(cm)与燃烧时间t(h)的函数关系用图象表示为图中的( B )
解析:由题意h=20-5t,0≤t≤4.结合图象知应选B.
2.“红豆生南国,春来发几枝?”如图给出了红豆生长时间t(月)与枝数y(枝)的散点图,那么红豆生长时间与枝数的关系用下列哪个函数模型拟合最好( C )
A.y=t3 B.y=log2t
C.y=2t D.y=2t2
解析:符合指数函数模型.
3.将进货单价为8元的商品按10元/个销售时,每天可卖出100个,若此商品的销售单价涨1元,日销售量就减少10个,为了获取最大利润,此商品的销售单价应定为14元.
解析:设销售单价应涨x元,则实际销售单价为(10+x)元,此时日销售量为(100-10x)个,
每个商品的利润为(10+x)-8=2+x(元),
∴总利润y=(2+x)(100-10x)=-10x2+80x+200
=-10(x-4)2+360(0∴当x=4时y有最大值,此时单价为14元.
4.在不考虑空气阻力的情况下,火箭的最大速度v米/秒和燃料的质量M千克、火箭(除燃料外)的质量m千克的函数关系式是v=2 000·ln(1+).当燃烧质量是火箭质量的e6-1倍时,火箭的最大速度可达12千米/秒.
解析:当v=12 000时,2 000·ln(1+)=12 000,
∴ln(1+)=6,∴=e6-1.
5.某学校准备购买一批电脑,在购买前进行的市场调查显示:在相同品牌、质量与售后服务的条件下,甲、乙两公司的报价都是每台6 000元.甲公司的优惠条件是购买10台以上的,从第11台开始按报价的七折计算,乙公司的优惠条件是均按八五折计算.
(1)分别写出在两公司购买电脑的总费用y甲,y乙与购买台数x之间的函数关系式;
(2)根据购买的台数,你认为学校应选择哪家公司更合算?
解:(1)y甲=
=
y乙=5 100x(x∈N),
(2)当x≤10时,显然y甲>y乙;
当x>10时,令y甲>y乙,
即4 200x+18 000>5 100x,解得x<20.
答:当购买的台数不超过20台时,应选择乙公司,当购买台数超过20台时,应选择甲公司.
——本课须掌握的三大问题
1.函数模型的应用实例主要包括三个方面:
(1)利用给定的函数模型解决实际问题;
(2)建立确定性的函数模型解决实际问题;
(3)建立拟合函数模型解决实际问题.
2.在引入自变量建立目标函数解决函数应用题时,一是要注意自变量的取值范围,二是要检验所得结果,必要时运用估算和近似计算,以使结果符合实际问题的要求.
3.在实际问题向数学问题的转化过程中,要充分使用数学语言,如引入字母,列表,画图等使实际问题数学符号化.
[目标] 1.会用分段函数模型或自建函数模型解决一些简单的实际问题;2.会根据所给数据选择合适的函数模型进行拟合.
[重点] 根据给定的函数模型解决实际问题.
[难点] 建立数学模型解答实际问题.
知识点一 解函数模型应用题的一般步骤
[填一填]
1.函数模型应用的两个方面
(1)利用已知函数模型解决问题;
(2)建立恰当的函数模型,并利用所得函数模型解释有关现象,对某些发展趋势进行预测.
2.解函数应用题的一般步骤
(1)审题:弄清题意,分清条件和结论,理顺数理关系.
(2)建模:将文字语言转化为数学语言,用数学知识建立相应的数学模型.
(3)求模:求解数学模型,得到数学结论.
(4)还原:将用数学方法得到的结论还原为实际问题.
[答一答]
1.常见的函数模型有哪些?
提示:(1)正比例函数模型:f(x)=kx(k为常数,k≠0);
(2)反比例函数模型:f(x)=(k为常数,k≠0);
(3)一次函数模型:f(x)=kx+b(k,b为常数,k≠0);
(4)二次函数模型:f(x)=ax2+bx+c(a,b,c为常数,a≠0);
(5)指数函数模型:f(x)=abx+c(a,b,c为常数,a≠0,b>0,b≠1);
(6)对数函数模型:f(x)=mlogax+n(m,n,a为常数,m≠0,a>0,a≠1);
(7)幂函数模型:f(x)=axn+b(a,b,n为常数,a≠0,n≠1).
知识点二 函数拟合与预测的一般步骤
[填一填]
(1)收集数据;
(2)画散点图;
(3)选择函数模型;
(4)求函数模型;
(5)检验.若符合实际情况,则用函数模型解释实际问题;若不符合实际情况则从(3)重新开始.
[答一答]
2.如何根据收集到的数据解决实际问题?
提示:通过收集数据直接去解决问题的一般过程如下:
第一步:收集数据;
第二步:根据收集到的数据在平面直角坐标系内画出散点图;
第三步:根据点的分布特征,选择一个能刻画散点图特征的函数模型;
第四步:选择其中的几组数据求出函数模型;
第五步:将已知数据代入所求出的函数模型进行检验,看其是否符合实际.若不符合实际,则重复第三、四、五步.若符合实际,则进入下一步;
第六步:用求得的函数模型去解释实际问题.
以上过程可用程序框图表示如下:
3.数据拟合时,得到的函数为什么需要检验?
提示:因为根据已给的数据作出散点图,一般是以比较熟悉的、最简单的函数作模拟,但所估计的函数有时可能误差较大或不切合客观实际,此时要重新调整数据或选用其他函数模型.
类型一 建立函数模型的应用题
[例1] 某汽车城销售某种型号的汽车,进货单价为25万元.市场调研表明:当销售单价为29万元时,平均每周能售出8辆,而当销售单价每降低0.5万元时,平均每周能多售出4辆.设每辆汽车降价x万元,每辆汽车的销售利润为y万元(每辆车的销售利润=销售单价-进货单价).
(1)求y与x之间的函数关系式,并在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的销售单价为多少万元时,平均每周的销售利润最大?最大利润是多少?
[分析] 解决本题需弄清楚:每辆车的销售利润=销售单价-进货单价;先求出每辆车的销售利润,再乘以售出辆数可得每周销售利润.通过二次函数求最值,可得汽车合适的销售单价.
[解] (1)因为y=29-25-x,
所以y=-x+4(0≤x≤4).
(2)z=(8+×4)y=(8x+8)(-x+4)=-8x2+24x+32(0≤x≤4).
(3)由(2)知,z=-8x2+24x+32=-8(x-1.5)2+50(0≤x≤4).故当x=1.5时,zmax=50.
所以当销售单价为29-1.5=27.5万元时,每周的销售利润最大,最大利润为50万元.
在函数模型中,二次函数模型占有重要的地位,因为根据实际问题建立函数解析式后,可利用配方法、判别式法、换元法、函数的单调性等来求函数的最值,从而解决实际问题中的最大、最小等问题.
[变式训练1] 据市场分析,烟台某海鲜加工公司当月产量在10吨至25吨时,月生产总成本y(万元)可以看成月产量x(吨)的二次函数;当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元,且为二次函数的顶点.
(1)写出月总成本y(万元)关于月产量x(吨)的函数关系式;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润?
解:(1)设y=a(x-15)2+17.5,
将x=10,y=20代入上式,得20=25a+17.5.
解得a=.
所以y=(x-15)2+17.5(10≤x≤25).
(2)设最大利润为Q(x),
则Q(x)=1.6x-y=1.6x-
=-(x-23)2+12.9(10≤x≤25).
因为x=23∈[10,25],
所以月产量为23吨时,可获最大利润12.9万元.
类型二 已知函数模型的应用题
[例2] 已知某产品市场价格与市场供应量P的关系近似满足P(x)=2(1-kt)(x-b)2(其中t为关税的税率,且t∈[0,),x为市场价格,b,k为正常数),当t=时的市场供应量曲线如图所示.
(1)根据图象求b,k的值;
(2)记市场需求量为Q,它近似满足Q(x)=211-,当P=Q时的价格称为市场平衡价格,为使市场平衡价格不低于9元,求税率的最小值.
[解] (1)由图象知:
??
(2)当P=Q时,有2(1-6t)(x-5)2=211-,
即(1-6t)(x-5)2=11-
?2(1-6t)==
=-.
令m=,则2(1-6t)=17m2-m.
∵x≥9,∴m∈(0,].
当m=时,2(1-6t)取最大值,故t≥,
即税率的最小值为.
(1(本题利用已知函数模型解决实际问题,首先利用给出的函数图象,通过待定系数法确定函数关系式,再利用函数关系式求最值,求最值时注意自变量的取值范围.
(2(对于题中已给出数学模型问题,只要解数学模型即可,较常用的方法是待定系数法解模型,然后利用相应的解析式及对应函数的性质解决实际问题.
[变式训练2] 灌满开水的热水瓶放在室内,如果瓶内开水原来的温度是θ1度,室内气温是θ0度,t分钟后,开水的温度可由公式θ=θ0+(θ1-θ0)e-kt求得,这里,k是一个与热水瓶类型有关的正的常量.现有一只某种类型的热水瓶,测得瓶内水温为100℃,过1小时后又测得瓶内水温变为98℃.已知某种奶粉必须用不低于85℃的开水冲调,现用这种类型的热水瓶在早上六点灌满100℃的开水,问:能否在这一天的中午十二点用这瓶开水来冲调上述奶粉?(假定该地白天室温为20℃)
解:根据题意,有98=20+(100-20)e-60k,
整理得e-60k=.
利用计算器,解得k=0.000 422 2.
故θ=20+80e-0.000 422 2t.
从早上六点至中午十二点共过去6小时,即360分钟.
当t=360时,θ=20+80e-0.000 422 2×360=20+80e-0.152,
由计算器算得θ≈88℃>85℃,
即能够在这一天的中午十二点用这瓶开水来冲调奶粉.
类型三 拟合函数模型的应用题
[例3] 某个体经营者把开始六个月试销A,B两种商品的逐月投资与所获纯利润列成下表:
该经营者准备下月投入12万元经营这两种产品,但不知投入A,B两种商品各多少万元才合算.请你帮助制定一个资金投入方案,使得该经营者能获得最大利润,并按你的方案求出该经营者下月可获得的最大纯利润(结果保留两个有效数字).
[分析] 只给出数据,没明确函数关系,这样就需要准确的画出散点图.然后根据图形选择合适的函数模型来解决实际问题.
[解] 以投资额为横坐标,纯利润为纵坐标,在平面直角坐标系中画出散点图,如图所示.
观察散点图可以看出,A种商品的所获纯利润y与投资额x之间的变化规律可以用二次函数模型进行模拟,如图①所示.
取(4,2)为最高点,则y=a(x-4)2+2,再把点(1,0.65)代入,得0.65=a(1-4)2+2,解得a=-0.15,所以y=-0.15(x-4)2+2.
B种商品所获纯利润y与投资额x之间的变化规律是线性的,可以用一次函数模型进行模拟,如图②所示.
设y=kx+b,取点(1,0.25)和(4,1)代入,
得解得所以y=0.25x.
即前六个月所获纯利润y关于月投资A种商品的金额x的函数关系式是y=-0.15(x-4)2+2;前六个月所获纯利润y关于月投资B种商品的金额x的函数关系式是y=0.25x.
设下月投入A,B两种商品的资金分别为xA,xB(万元),总利润为W(万元),
那么
所以W=-0.15(xA-)2+0.15×()2+2.6.
当xA=≈3.2(万元)时,W取最大值,约为4.1万元,此时xB≈8.8(万元).
即该经营者下月把12万元中的3.2万元投资A种商品,8.8万元投资B种商品,可获得最大利润约为4.1万元.
拟合数据,建立函数模型解决实际问题的一般步骤:根据收集到的数据作出散点图,然后根据散点图的形状,选用比较接近的可能的函数模型来描述所涉及的数量之间的关系,然后利用待定系数法确定出具体的函数解析式,若符合实际,可用此函数模型解释问题,若不符合实际,则继续选择模型,重复操作过程.
[变式训练3] 我国2014年至2017年国内生产总值(单位:万亿元)如下表所示:
年份
2014
2015
2016
2017
x
0
1
2
3
生产总值y
8.206 7
8.944 2
9.593 3
10.239 8
(1)画出函数图象,猜想它们之间的函数关系,近似地写出一个函数关系式;
(2)利用得出的关系式求生产总值,与表中实际生产总值比较.
解:
(1)画出函数图象,如图所示,从函数的图象可以看出,画出的点近似地落在一条直线上,设所求的一次函数为y=kx+b(k≠0).
把点(0,8.206 7)和(3,10.239 8)的坐标代入上式,解方程组,得
因此所求的函数关系式为y=0.677 7x+8.206 7.
(2)由得到的关系式计算出2015年和2016年的国内生产总值分别为0.677 7×1+8.206 7=8.884 4(万亿元),
0.677 7×2+8.206 7=9.562 1(万亿元).
与实际的生产总值相比,误差不超过0.1万亿元.
1.一根蜡烛长20 cm,点燃后每小时燃烧5 cm,燃烧时剩下的高度h(cm)与燃烧时间t(h)的函数关系用图象表示为图中的( B )
解析:由题意h=20-5t,0≤t≤4.结合图象知应选B.
2.“红豆生南国,春来发几枝?”如图给出了红豆生长时间t(月)与枝数y(枝)的散点图,那么红豆生长时间与枝数的关系用下列哪个函数模型拟合最好( C )
A.y=t3 B.y=log2t
C.y=2t D.y=2t2
解析:符合指数函数模型.
3.将进货单价为8元的商品按10元/个销售时,每天可卖出100个,若此商品的销售单价涨1元,日销售量就减少10个,为了获取最大利润,此商品的销售单价应定为14元.
解析:设销售单价应涨x元,则实际销售单价为(10+x)元,此时日销售量为(100-10x)个,
每个商品的利润为(10+x)-8=2+x(元),
∴总利润y=(2+x)(100-10x)=-10x2+80x+200
=-10(x-4)2+360(0
4.在不考虑空气阻力的情况下,火箭的最大速度v米/秒和燃料的质量M千克、火箭(除燃料外)的质量m千克的函数关系式是v=2 000·ln(1+).当燃烧质量是火箭质量的e6-1倍时,火箭的最大速度可达12千米/秒.
解析:当v=12 000时,2 000·ln(1+)=12 000,
∴ln(1+)=6,∴=e6-1.
5.某学校准备购买一批电脑,在购买前进行的市场调查显示:在相同品牌、质量与售后服务的条件下,甲、乙两公司的报价都是每台6 000元.甲公司的优惠条件是购买10台以上的,从第11台开始按报价的七折计算,乙公司的优惠条件是均按八五折计算.
(1)分别写出在两公司购买电脑的总费用y甲,y乙与购买台数x之间的函数关系式;
(2)根据购买的台数,你认为学校应选择哪家公司更合算?
解:(1)y甲=
=
y乙=5 100x(x∈N),
(2)当x≤10时,显然y甲>y乙;
当x>10时,令y甲>y乙,
即4 200x+18 000>5 100x,解得x<20.
答:当购买的台数不超过20台时,应选择乙公司,当购买台数超过20台时,应选择甲公司.
——本课须掌握的三大问题
1.函数模型的应用实例主要包括三个方面:
(1)利用给定的函数模型解决实际问题;
(2)建立确定性的函数模型解决实际问题;
(3)建立拟合函数模型解决实际问题.
2.在引入自变量建立目标函数解决函数应用题时,一是要注意自变量的取值范围,二是要检验所得结果,必要时运用估算和近似计算,以使结果符合实际问题的要求.
3.在实际问题向数学问题的转化过程中,要充分使用数学语言,如引入字母,列表,画图等使实际问题数学符号化.
