湘教版七年级数学上册第3章 一元一次方程3.3 一元一次方程的解法教学课件(共36张)
文档属性
| 名称 | 湘教版七年级数学上册第3章 一元一次方程3.3 一元一次方程的解法教学课件(共36张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-12 00:00:00 | ||
图片预览










文档简介
(共36张PPT)
一元一次方程的解法
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
丢番图的墓志铭
“坟中安葬着丢番图,多么令人惊讶!它忠实地记录了所经历的道路。上帝给予的童年占六分之一,又过十二分之一,两颊长胡。再过七分之一,点燃结婚的蜡烛。五年之后天赐贵子,可怜迟到的宁馨儿,享年仅及其父之半,便进入冰冷的墓。悲伤只有用数论的研究去弥补,又过四年,他也走完了人生的旅途。”
你知道丢番图去世时的年龄吗?请你列出方程
来算一算.
思考
新课导入
想一想
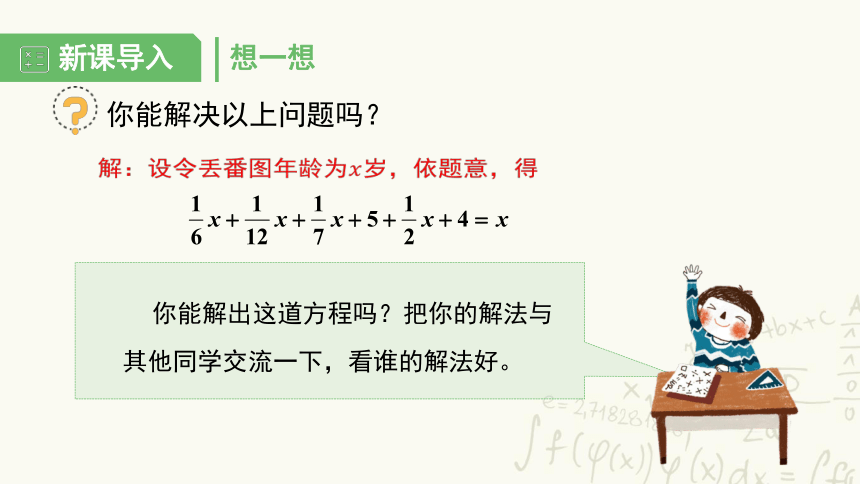
你能解决以上问题吗?
解:设令丢番图年龄为岁,依题意,得
你能解出这道方程吗?把你的解法与其他同学交流一下,看谁的解法好。
新课导入
某探险家在2002年乘热气球在24h内连续飞行5129km。已知热气球在前12h飞行了2345km,求热气球在后12h飞行的平均速度。
解析:若设后12h飞行的平均速度为km/h,则根据题意,可列方程:
2345 + 12x = 5129.
该如何求出x的值?
02 新知探究
新知探究
用移项解一元一次方程
请运用等式的性质解下列方程
(1) 4x - 15 = 9
解:两边都减去 5x ,得
-3x=-21.
系数化为1,得
x = 6.
(2) 2x = 5x -21
解:两边都加上 15 ,得
系数化为1,得
x = 7.
合并同类项 ,得
合并同类项 ,得
4x = 24.
2x = 5x – 21
4x – 15 = 9
+ 15
+ 15
–5x
–5x
4x= 9+15.
2x -5x = -21.
你能发现什么吗?
新知探究
移项
4x -15 = 9
①
4x = 9 +15
②
这个变形相当于把①中的 “– 15”这一项
由方程①
到方程 ② ,
“– 15”这项移动后,发生了什么变化?
改变了符号
从方程的左边移到了方程的右边.
-15
4x-15 = 9
4x = 9+15
新知探究
想一想
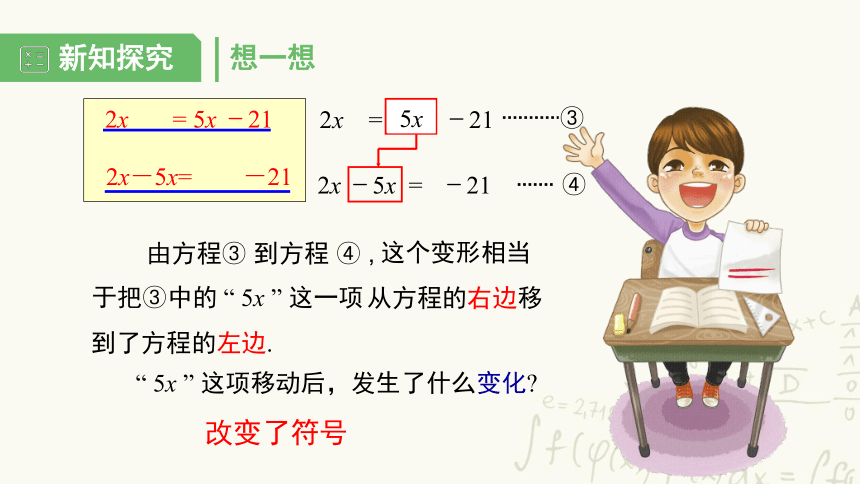
2x = 5x -21
③
2x -5x = -21
④
这个变形相当于把③中的 “ 5x ” 这一项
由方程③
到方程 ④ ,
“ 5x ” 这项移动后,发生了什么变化?
改变了符号
从方程的右边移到了方程的左边.
5x
2x = 5x -21
2x-5x= -21
新知探究
移项概念
一般地,把方程中某一项改变符号后,
从方程的一边移到另一边,这种变形叫做移项.
2x = 5x – 21
2x –5x = – 21
4x –15 = 9
4x = 9 +15
移项目的
一般地,把所有含有未知数的项移到方程的左边,把所有常数项移到方程的右边,使得一元一次方程更接近“x =a”的形式.
注:移项要变号
移项定义
新知探究
练一练
1.下列移项正确的是 ( )
A. 由2+x=8,得到x=8+2
B. 由5x=-8+x,得到5x+x= -8
C. 由4x=2x+1,得到4x-2x=1
D. 由5x-3=0,得到5x=-3
C
新知探究
合并同类项
4(x+0.5)+x=20-3
如何解这个带有括号方程?
解:去括号,得
移项,得 4x+x=17-2
4x+2+x=17
合并同类项,得 5x=15
方程两边同除以5,得x=3
新知探究
小归纳
移 项
合并同类项
系数化为1
去括号
归纳总结
通过以上解方程的过程,你能总结出解含有括号一元一次方程的一般步骤吗?
新知探究
想一想
下面方程的求解是否正确?如不正确,请改正.
解方程 2(2x+3)=2+x
解 去括号,得 4x+3=2+x
移项,得 4x +x = 2-3
化简,得 5x = -1
方程两边都除以5 ,得
x = -
应改为4 x +6 =2+x
应改为4 x– x = 2-6
应改为3x =-4
应改为 x =
方程两边都除以3,得
新知探究
去括号
可利用去括号解方程.
你有不同的解法吗?
解方程:
解:去括号,得
移项、合并同类项,得
两边同时除以(或同乘)得
解法一:
新知探究
去分母
解法二:
去分母,得4(x+14)=7(x+20).
方程两边同除以-3,得x=-28.
移项、合并同类项,得-3x=84.
去括号,得4x+56=7x+140.
把分数化成整数计算更简单!
思考:两种解法有什么不同?你认为哪种解法比较好?
解方程:
新知探究
小归纳
1. 去分母时,应在方程的左右两边乘以分母
的 ;
2. 去分母的依据是 ,去分母时不能
漏乘 ;
3. 要把分子(如果是一个多项式)作为一个整
体____________.
最小公倍数
等式性质2
没有分母的项
加上括号
新知探究
想一想
方程的左、右两边同时乘各分母的最小公倍数可去掉分母.
依据是等式的性质2.
解法二中如何把方程中的分母化去的?依据是什么?
?
×28
结论
新知探究
练一练
下列方程的解法对不对?如果不对,你能找出错在哪里吗?
解方程:
解:去分母,得 4x-1-3x + 6 = 1
移项,合并同类项,得 x=4
方程右边的“1”去分母时漏乘最小公倍数6
去括号符号错误
约去分母3后,(2x-1)×2在去括号时出错
03 典型例题
例题讲解
1.解下列方程:
(1) 5x-7=2x-10;
(2) -0.3x+3=9+1.2x.
解:(1) 移项,得
5x-2x=-10+7,
合并同类项,得
3x=-3,
系数化为1,得
x=-1.
(2) 移项,得
-0.3x-1.2x=9-3,
合并同类项,得
-1.5x=6,
系数化为1,得
x=-4.
练一练
例题讲解
2.如果x=-7是方程4x+6=ax-1的解,试求代数式 的值.
解:把x=-7代入方程,得
4×(-7)+6=a×(-7)-1,
解得a=3.
把a=3代入, .
练一练
例题讲解
3.解下列方程:
解:去括号,得
移项,得
合并同类项,得
两边同时除以-6,得
练一练
4.选择
(1)通过移项将下列方程变形,正确的是 ( )
A. 由5x-7=2,得5x=2-7
B. 由6x-3=x+4,得3-6x=4+x
C. 由8-x=x-5,得-x-x=-5-8
D. 由x+9=3x-1,得3x-x=-1+9
C
(2)若方程:3(2x-1)=2-3x的解与关于x的方程6-2k=2(x+3)相同,则k的值为( )
B
例题讲解
5.填空
(3)当x =_____时,式子 2x-1 的值比式子 5x+6 的值小1.
(1)已知 2m-3=3n+1,则 2m-3n = .
(2)如果 与 互为相反数,则m的值为 .
4
-2
例题讲解
6.解下列方程:
解析:
(1)
(2)
例题讲解
(1) 6x =-2(3x-5) +10; (2) -2(x+5)=3(x-5)-6
7.解下列方程
解:
(1) 6x=-2(3x-5)+10
6x=-6x+10+10
6x +6x=10+10
12x=20
(2) -2(x+5)=3(x-5)-6
-2x-10=3x-15-6
-5x=-11
例题讲解
04 拓展提高
拓展提高
应用
1.某羽毛球协会组织一些会员到现场观看某场比赛.已知该协会购买了每张300元和每张400元的两种门票共8张,总费用为2700元.请问该协会购买了这两种门票各多少张?
解:设每张300元的门票买了x张,
则每张400元的门票买了(8-x)张,
由题意得:300x+400×(8-x)=2700,
解之得 x=5,
∴买400元每张的门票张数为8-5=3(张).
答:每张300元的门票买了5张,每张400元的门票买了3张.
拓展提高
应用
2.有一人问老师,他所教的班级有多少名学生,老师说:“一半学生在学数学,四分之一的学生在学音乐,七分之一的学生在学外语,还剩六位学生正在操场踢足球.”你知道这个班有多少学生吗?
答:这个班有56名学生.
解:设这个班有x名学生,依题意得
解之得 x=56.
05 课堂小结
课堂小结
变形名称 具体的做法
去分母 乘所有的分母的最小公倍数.
依据是等式性质二.
去括号 先去小括号,再去中括号,最后去大括号.依据是去括号法则和乘法分配律.
移项 把含有未知数的项移到一边,常数项移到另一边.“过桥变号”,依据是等式性质一.
合并同类项 将未知数的系数相加,常数项相加.
依据是乘法分配律.
系数化为1 在方程的两边除以未知数的系数.
依据是等式性质二.
解一元一次方程的一般步骤
06 作业布置
作业布置
课本习题A组第1、2、3题.
谢 谢 观 看
一元一次方程的解法
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
丢番图的墓志铭
“坟中安葬着丢番图,多么令人惊讶!它忠实地记录了所经历的道路。上帝给予的童年占六分之一,又过十二分之一,两颊长胡。再过七分之一,点燃结婚的蜡烛。五年之后天赐贵子,可怜迟到的宁馨儿,享年仅及其父之半,便进入冰冷的墓。悲伤只有用数论的研究去弥补,又过四年,他也走完了人生的旅途。”
你知道丢番图去世时的年龄吗?请你列出方程
来算一算.
思考
新课导入
想一想
你能解决以上问题吗?
解:设令丢番图年龄为岁,依题意,得
你能解出这道方程吗?把你的解法与其他同学交流一下,看谁的解法好。
新课导入
某探险家在2002年乘热气球在24h内连续飞行5129km。已知热气球在前12h飞行了2345km,求热气球在后12h飞行的平均速度。
解析:若设后12h飞行的平均速度为km/h,则根据题意,可列方程:
2345 + 12x = 5129.
该如何求出x的值?
02 新知探究
新知探究
用移项解一元一次方程
请运用等式的性质解下列方程
(1) 4x - 15 = 9
解:两边都减去 5x ,得
-3x=-21.
系数化为1,得
x = 6.
(2) 2x = 5x -21
解:两边都加上 15 ,得
系数化为1,得
x = 7.
合并同类项 ,得
合并同类项 ,得
4x = 24.
2x = 5x – 21
4x – 15 = 9
+ 15
+ 15
–5x
–5x
4x= 9+15.
2x -5x = -21.
你能发现什么吗?
新知探究
移项
4x -15 = 9
①
4x = 9 +15
②
这个变形相当于把①中的 “– 15”这一项
由方程①
到方程 ② ,
“– 15”这项移动后,发生了什么变化?
改变了符号
从方程的左边移到了方程的右边.
-15
4x-15 = 9
4x = 9+15
新知探究
想一想
2x = 5x -21
③
2x -5x = -21
④
这个变形相当于把③中的 “ 5x ” 这一项
由方程③
到方程 ④ ,
“ 5x ” 这项移动后,发生了什么变化?
改变了符号
从方程的右边移到了方程的左边.
5x
2x = 5x -21
2x-5x= -21
新知探究
移项概念
一般地,把方程中某一项改变符号后,
从方程的一边移到另一边,这种变形叫做移项.
2x = 5x – 21
2x –5x = – 21
4x –15 = 9
4x = 9 +15
移项目的
一般地,把所有含有未知数的项移到方程的左边,把所有常数项移到方程的右边,使得一元一次方程更接近“x =a”的形式.
注:移项要变号
移项定义
新知探究
练一练
1.下列移项正确的是 ( )
A. 由2+x=8,得到x=8+2
B. 由5x=-8+x,得到5x+x= -8
C. 由4x=2x+1,得到4x-2x=1
D. 由5x-3=0,得到5x=-3
C
新知探究
合并同类项
4(x+0.5)+x=20-3
如何解这个带有括号方程?
解:去括号,得
移项,得 4x+x=17-2
4x+2+x=17
合并同类项,得 5x=15
方程两边同除以5,得x=3
新知探究
小归纳
移 项
合并同类项
系数化为1
去括号
归纳总结
通过以上解方程的过程,你能总结出解含有括号一元一次方程的一般步骤吗?
新知探究
想一想
下面方程的求解是否正确?如不正确,请改正.
解方程 2(2x+3)=2+x
解 去括号,得 4x+3=2+x
移项,得 4x +x = 2-3
化简,得 5x = -1
方程两边都除以5 ,得
x = -
应改为4 x +6 =2+x
应改为4 x– x = 2-6
应改为3x =-4
应改为 x =
方程两边都除以3,得
新知探究
去括号
可利用去括号解方程.
你有不同的解法吗?
解方程:
解:去括号,得
移项、合并同类项,得
两边同时除以(或同乘)得
解法一:
新知探究
去分母
解法二:
去分母,得4(x+14)=7(x+20).
方程两边同除以-3,得x=-28.
移项、合并同类项,得-3x=84.
去括号,得4x+56=7x+140.
把分数化成整数计算更简单!
思考:两种解法有什么不同?你认为哪种解法比较好?
解方程:
新知探究
小归纳
1. 去分母时,应在方程的左右两边乘以分母
的 ;
2. 去分母的依据是 ,去分母时不能
漏乘 ;
3. 要把分子(如果是一个多项式)作为一个整
体____________.
最小公倍数
等式性质2
没有分母的项
加上括号
新知探究
想一想
方程的左、右两边同时乘各分母的最小公倍数可去掉分母.
依据是等式的性质2.
解法二中如何把方程中的分母化去的?依据是什么?
?
×28
结论
新知探究
练一练
下列方程的解法对不对?如果不对,你能找出错在哪里吗?
解方程:
解:去分母,得 4x-1-3x + 6 = 1
移项,合并同类项,得 x=4
方程右边的“1”去分母时漏乘最小公倍数6
去括号符号错误
约去分母3后,(2x-1)×2在去括号时出错
03 典型例题
例题讲解
1.解下列方程:
(1) 5x-7=2x-10;
(2) -0.3x+3=9+1.2x.
解:(1) 移项,得
5x-2x=-10+7,
合并同类项,得
3x=-3,
系数化为1,得
x=-1.
(2) 移项,得
-0.3x-1.2x=9-3,
合并同类项,得
-1.5x=6,
系数化为1,得
x=-4.
练一练
例题讲解
2.如果x=-7是方程4x+6=ax-1的解,试求代数式 的值.
解:把x=-7代入方程,得
4×(-7)+6=a×(-7)-1,
解得a=3.
把a=3代入, .
练一练
例题讲解
3.解下列方程:
解:去括号,得
移项,得
合并同类项,得
两边同时除以-6,得
练一练
4.选择
(1)通过移项将下列方程变形,正确的是 ( )
A. 由5x-7=2,得5x=2-7
B. 由6x-3=x+4,得3-6x=4+x
C. 由8-x=x-5,得-x-x=-5-8
D. 由x+9=3x-1,得3x-x=-1+9
C
(2)若方程:3(2x-1)=2-3x的解与关于x的方程6-2k=2(x+3)相同,则k的值为( )
B
例题讲解
5.填空
(3)当x =_____时,式子 2x-1 的值比式子 5x+6 的值小1.
(1)已知 2m-3=3n+1,则 2m-3n = .
(2)如果 与 互为相反数,则m的值为 .
4
-2
例题讲解
6.解下列方程:
解析:
(1)
(2)
例题讲解
(1) 6x =-2(3x-5) +10; (2) -2(x+5)=3(x-5)-6
7.解下列方程
解:
(1) 6x=-2(3x-5)+10
6x=-6x+10+10
6x +6x=10+10
12x=20
(2) -2(x+5)=3(x-5)-6
-2x-10=3x-15-6
-5x=-11
例题讲解
04 拓展提高
拓展提高
应用
1.某羽毛球协会组织一些会员到现场观看某场比赛.已知该协会购买了每张300元和每张400元的两种门票共8张,总费用为2700元.请问该协会购买了这两种门票各多少张?
解:设每张300元的门票买了x张,
则每张400元的门票买了(8-x)张,
由题意得:300x+400×(8-x)=2700,
解之得 x=5,
∴买400元每张的门票张数为8-5=3(张).
答:每张300元的门票买了5张,每张400元的门票买了3张.
拓展提高
应用
2.有一人问老师,他所教的班级有多少名学生,老师说:“一半学生在学数学,四分之一的学生在学音乐,七分之一的学生在学外语,还剩六位学生正在操场踢足球.”你知道这个班有多少学生吗?
答:这个班有56名学生.
解:设这个班有x名学生,依题意得
解之得 x=56.
05 课堂小结
课堂小结
变形名称 具体的做法
去分母 乘所有的分母的最小公倍数.
依据是等式性质二.
去括号 先去小括号,再去中括号,最后去大括号.依据是去括号法则和乘法分配律.
移项 把含有未知数的项移到一边,常数项移到另一边.“过桥变号”,依据是等式性质一.
合并同类项 将未知数的系数相加,常数项相加.
依据是乘法分配律.
系数化为1 在方程的两边除以未知数的系数.
依据是等式性质二.
解一元一次方程的一般步骤
06 作业布置
作业布置
课本习题A组第1、2、3题.
谢 谢 观 看
同课章节目录
