湘教版七年级数学上册第3章 一元一次方程3.4 一元一次方程模型的应用教学课件(共36张)
文档属性
| 名称 | 湘教版七年级数学上册第3章 一元一次方程3.4 一元一次方程模型的应用教学课件(共36张) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-12 00:00:00 | ||
图片预览










文档简介
(共36张PPT)
一元一次方程模型的应用
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
老师和小明相距10米,他们同时出发,相向而行,老师每秒走3米,小明每秒走4米,他们能相遇吗?几秒钟可以相遇?
等量关系:
所用公式:路程=速度×时间
想一想
老师走的路程+小明走的路程=相距的路程
新课导入
想一想
某湿地公园举行观鸟节活动,其门票售出情况如下:该公园共售出 1200 张门票, 得总票款 20000 元,问全价票和半价票各售出多少张?(票价如图所示)
02 新知探究
新知探究
某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹得票款69500元,成人票与学生票各售出多少张?
成人票 80元
学生票 50元
成人票数+__________=1000张; ?
__________+学生票款=__________.?
分析题意可得此题中的等量关系有:
学生票数
成人票款
69500元
票价问题
解析:
新知探究
票价问题
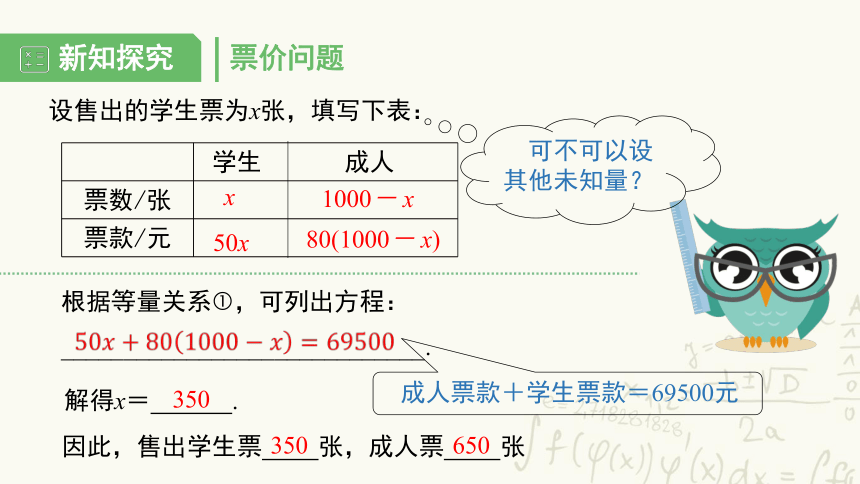
设售出的学生票为x张,填写下表:
学生 成人
票数/张
票款/元
根据等量关系?,可列出方程:
_____________________________.
解得x= .
因此,售出学生票 张,成人票 张
x
1000- x
50x
80(1000- x)
成人票款+学生票款=69500元
350
350
650
可不可以设其他未知量?
新知探究
票价问题
设所得的学生票款为 y 元,填写下表:
学生 成人
票款/元
票数/张
根据等量关系②,可列出方程
_______________________.
解得y= .
因此,售出成人票 张,学生票 张
y/50
(69500- y)/80
y
69500- y
17500
650
350
成人票数+学生票款数=1000张
17500÷50=350(张)
y/50
新知探究
当问题中含有两个未知量、两个等量关系时,可以把其中一个未知量设为未知数,另一个未知量(根据其中一个等量关系)用含未知数的代数式表示,而另一个等量关系则用来列方程.
小归纳
新知探究
练一练
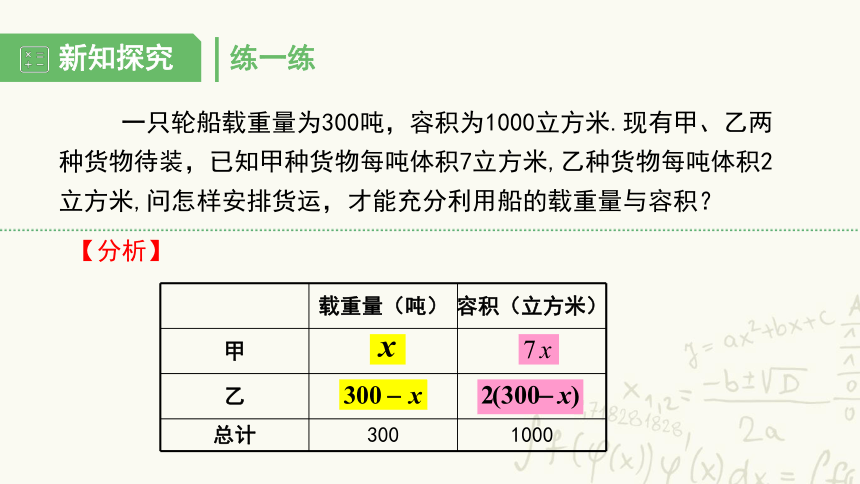
一只轮船载重量为300吨,容积为1000立方米.现有甲、乙两种货物待装,已知甲种货物每吨体积7立方米,乙种货物每吨体积2立方米,问怎样安排货运,才能充分利用船的载重量与容积?
载重量(吨) 容积(立方米)
甲
乙
总计 300 1000
【分析】
新知探究
1.进价100元的商品提价40%后,标价为________元,若按标价的八折销售,则售价为________元,此商品的利润为________元,利润率是________.
2.某商品原价是a元,现在每件打九折销售,则此时的售价是___ 元.
140
112
12
0.9a
12%
填空:
销售问题
新知探究
想一想
思考:上面的问题中存在哪些量?
成本价(进价);
标价 (原价);
销售价;
利润;盈利;亏损;
利润率;
这些量有何
关系?
折扣数.
新知探究
小归纳
商品利润
利润率=
= 商品售价-商品进价
● 售价、进价、利润的关系:
商品利润
● 进价、利润、利润率的关系:
商品进价
×100%
折扣数
●标价、折扣数、商品售价的关系:
商品售价=
标价×
10
●商品售价、进价、利润率的关系:
商品进价
商品售价=
×(1+利润率)
销
售
中
的
数
量
关
系
新知探究
(1) 某商品的进价为80元,在进价的基础上提高20%后
标价,则标价为 元.
(2) 标价为500元的商品打9折后的售价为 元.
(3) 某商品每件的销售利润是72元,进价是120元,则售
价是 元.
(4) 某商品利润率为13%,进价为50元,则利润是 元.
(80+80×20%)
(500×0.9)
(50×13%)
(120+72)
96
450
6.5
192
练一练
新知探究
为鼓励居民节约用水,某市出台了新的家庭用水收费标准,规定:所交水费分为标准内水费与超标部分水费两部分,其中标准内水费为1.96 元/ t,超标部分水费为2.94元/t. 某家庭6月份用水12t,需交水费27.44元.求该市规定的家庭月标准用水量.
费用问题
新知探究
费用问题
本问题首先要判断所交水费27.44元中是否含有超标部分,
由于1.96×12 = 23.52(元),小于27.44元,
因此所交水费中含有超标部分的水费,
月标准内水费+超标部分的水费=该月所交水费.
等量关系:
解析:
新知探究
练一练
设家庭月标准用水量为x t,
根据等量关系,得
1.96x +(12-x)×2.94 = 27.44.
解之得 x = 8 .
答:该市家庭月标准用水量为8 t.
解:
新知探究
小归纳
正如水费这种分段计费问题的解答,首先要考虑收费是在哪一段, 所用水(电)是否超过标准.
如果在标准内,那么所交费用=标准内费率×所用水(电)量;如果超过标准,那么所交费用=标准内费用+超过标准的费用,即为:所交费用=标准内费率×标准量+标准外费率×超过标准的量.
新知探究
间隔问题
某道路一侧原有路灯106盏(两端都有),相邻两盏灯的距离为36m,现计划全部更换为新型的节能灯,且相邻两盏灯的距离变为70m,则需安装新型节能灯多少盏?
答:需安装新型节能灯55盏.
36m
设需安装x盏新型节能灯盏,根据示意图所示,106盏灯共存在(106-1)=105个间隙。
解之得:
解析:
新知探究
方法总结
间隔问题应用比较普遍,如路边种树,街道装路灯等.
需要注意:
(1)两个端点都种上树(装上灯),则树数-1=间隔数;
(2)两个端点都不种树(装上灯),则树数+1=间隔数.
03 典型例题
例题讲解
1.某房间里有四条腿的椅子和三条腿的凳子共16个,如果椅子腿数与凳子腿数的和为60条,有几张椅子和几条凳子?
【分析】本问题中涉及的等量关系有:
椅子数+凳子数=16,椅子腿数+凳子腿数=60.
解:设有x 张椅子,则有(16-x)条凳子.
根据题意,得4x+ 3(16-x)=60 .
解得 x = 12 .
凳子数为16-12=4(条).
答:有12张椅子,4条凳子.
例题讲解
2.王大伯3年前把手头一笔钱作为3年定期存款存入银行,年利率为5%.到期后得到本息共23000元,问当年王大伯存入银行多少钱?
解:设当年王大伯存入银行x元,年利率为5%,存期3年,所以3年的利息为3×5% x元.3年到期后本息共23000元.
根据题意,得 x +3×5% x =23000
解方程,得 x =20000
答:当年王大伯存入银行20000元.
例题讲解
3.小明与小红的家相距 20 km, 小明从家里出发骑自行车去小红家,两人商定小红到时候从家里出发骑自行车去接小明. 已知小明骑车的速度为13 km/h, 小红骑车的速度是 12 km/h.
(1) 如果两人同时出发,那么他们经过多少小时相遇?
(2) 如果小明先走 30 min,那么小红骑车要走多少小时才能与小明相遇?
例题讲解
解:(1) 设小明与小红骑车走了 x h 后相遇, 则根据等量关系,
得13x + 12x = 20 .解得 x = 0.8 .
(2) 设小红骑车走了 t h 后与小明相遇, 则根据等量关系, 得
13 ( 0.5+ t )+ 12t = 20 .解得 t = 0.54 .
答:(1)经过 0.8 h 他们两人相遇(2)小红骑车走 0.54 h 后与小明相遇.
4.选择
(1)甲、乙两人练习赛跑,甲每秒跑4米,乙每秒跑6米,甲先跑10秒,乙开始跑,设乙x秒后追上甲,依题意列方程得( )
A.6x =4x B. 6x=4x+40
C.6x= 4x-40 D. 4x+10=6x
B
A.12.5千米/时 B.15千米/时
C.17.5千米/时 D.20千米/时
(2)甲、乙两人骑自行车同时从相距65千米的两地相向而行,2小时相遇,若甲比乙每小时多骑2.5千米,则乙的时速是( )
B
例题讲解
5.填空
某商场把进价为1980元的商品按标价的八折出售,仍获利10%, 则该商品的标价为 元.
分析:
设标价为x元,按标价的八折出售为80%?x;按1980元出售获利80%x - 1980;根据题意可得80%?x-1980=10%×1980;解可得答案.
解答:
设标价为x元,
则依题意可列方程:80%?x - 1980=10%×1980;
解得x =2722.5.
2722.5
例题讲解
04 拓展提高
拓展提高
应用
1.某商场将某种商品按原价的8折出售,此时商品的利润率 10%。已知这种商品的进价为1800元,那么这种商品的原价是多少?
分析:利润率= = 。在解决这个问题的过程中,要抓住这个等量关系。由于本例中只提到售价、进价和利润率,因此我们可以用“进价”代替“成本”。
解这个方程,得 x =2475.
因此,这种商品的原价为2475元。
成本
售价-成本
解:设商品原价是x元,根据题意,得
拓展提高
应用
2.一队学生去校外进行军事野营训练,他们以5km/h的速度行进,走了18 min的时候,学校要将一个紧急通知传给队长,通讯员从学校出发,骑自行车以14 km/h的速度按原路追上去,通讯员用多少时间可以追上学生的队伍?
05 课堂小结
课堂小结
问题的已
知条件
解决行程问题的基本步骤:
画出线
段图
找出等
量关系
列方程
并求解
回答
同向追及问题
同地不同时:
同时不同地:
甲路程+路程差=乙路程;
甲路程=乙路程
相向相遇问题
甲的路程+乙的路程=总路程
重点理解行程问题
06 作业布置
作业布置
课后练习1、2题
谢 谢 观 看
一元一次方程模型的应用
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
老师和小明相距10米,他们同时出发,相向而行,老师每秒走3米,小明每秒走4米,他们能相遇吗?几秒钟可以相遇?
等量关系:
所用公式:路程=速度×时间
想一想
老师走的路程+小明走的路程=相距的路程
新课导入
想一想
某湿地公园举行观鸟节活动,其门票售出情况如下:该公园共售出 1200 张门票, 得总票款 20000 元,问全价票和半价票各售出多少张?(票价如图所示)
02 新知探究
新知探究
某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹得票款69500元,成人票与学生票各售出多少张?
成人票 80元
学生票 50元
成人票数+__________=1000张; ?
__________+学生票款=__________.?
分析题意可得此题中的等量关系有:
学生票数
成人票款
69500元
票价问题
解析:
新知探究
票价问题
设售出的学生票为x张,填写下表:
学生 成人
票数/张
票款/元
根据等量关系?,可列出方程:
_____________________________.
解得x= .
因此,售出学生票 张,成人票 张
x
1000- x
50x
80(1000- x)
成人票款+学生票款=69500元
350
350
650
可不可以设其他未知量?
新知探究
票价问题
设所得的学生票款为 y 元,填写下表:
学生 成人
票款/元
票数/张
根据等量关系②,可列出方程
_______________________.
解得y= .
因此,售出成人票 张,学生票 张
y/50
(69500- y)/80
y
69500- y
17500
650
350
成人票数+学生票款数=1000张
17500÷50=350(张)
y/50
新知探究
当问题中含有两个未知量、两个等量关系时,可以把其中一个未知量设为未知数,另一个未知量(根据其中一个等量关系)用含未知数的代数式表示,而另一个等量关系则用来列方程.
小归纳
新知探究
练一练
一只轮船载重量为300吨,容积为1000立方米.现有甲、乙两种货物待装,已知甲种货物每吨体积7立方米,乙种货物每吨体积2立方米,问怎样安排货运,才能充分利用船的载重量与容积?
载重量(吨) 容积(立方米)
甲
乙
总计 300 1000
【分析】
新知探究
1.进价100元的商品提价40%后,标价为________元,若按标价的八折销售,则售价为________元,此商品的利润为________元,利润率是________.
2.某商品原价是a元,现在每件打九折销售,则此时的售价是___ 元.
140
112
12
0.9a
12%
填空:
销售问题
新知探究
想一想
思考:上面的问题中存在哪些量?
成本价(进价);
标价 (原价);
销售价;
利润;盈利;亏损;
利润率;
这些量有何
关系?
折扣数.
新知探究
小归纳
商品利润
利润率=
= 商品售价-商品进价
● 售价、进价、利润的关系:
商品利润
● 进价、利润、利润率的关系:
商品进价
×100%
折扣数
●标价、折扣数、商品售价的关系:
商品售价=
标价×
10
●商品售价、进价、利润率的关系:
商品进价
商品售价=
×(1+利润率)
销
售
中
的
数
量
关
系
新知探究
(1) 某商品的进价为80元,在进价的基础上提高20%后
标价,则标价为 元.
(2) 标价为500元的商品打9折后的售价为 元.
(3) 某商品每件的销售利润是72元,进价是120元,则售
价是 元.
(4) 某商品利润率为13%,进价为50元,则利润是 元.
(80+80×20%)
(500×0.9)
(50×13%)
(120+72)
96
450
6.5
192
练一练
新知探究
为鼓励居民节约用水,某市出台了新的家庭用水收费标准,规定:所交水费分为标准内水费与超标部分水费两部分,其中标准内水费为1.96 元/ t,超标部分水费为2.94元/t. 某家庭6月份用水12t,需交水费27.44元.求该市规定的家庭月标准用水量.
费用问题
新知探究
费用问题
本问题首先要判断所交水费27.44元中是否含有超标部分,
由于1.96×12 = 23.52(元),小于27.44元,
因此所交水费中含有超标部分的水费,
月标准内水费+超标部分的水费=该月所交水费.
等量关系:
解析:
新知探究
练一练
设家庭月标准用水量为x t,
根据等量关系,得
1.96x +(12-x)×2.94 = 27.44.
解之得 x = 8 .
答:该市家庭月标准用水量为8 t.
解:
新知探究
小归纳
正如水费这种分段计费问题的解答,首先要考虑收费是在哪一段, 所用水(电)是否超过标准.
如果在标准内,那么所交费用=标准内费率×所用水(电)量;如果超过标准,那么所交费用=标准内费用+超过标准的费用,即为:所交费用=标准内费率×标准量+标准外费率×超过标准的量.
新知探究
间隔问题
某道路一侧原有路灯106盏(两端都有),相邻两盏灯的距离为36m,现计划全部更换为新型的节能灯,且相邻两盏灯的距离变为70m,则需安装新型节能灯多少盏?
答:需安装新型节能灯55盏.
36m
设需安装x盏新型节能灯盏,根据示意图所示,106盏灯共存在(106-1)=105个间隙。
解之得:
解析:
新知探究
方法总结
间隔问题应用比较普遍,如路边种树,街道装路灯等.
需要注意:
(1)两个端点都种上树(装上灯),则树数-1=间隔数;
(2)两个端点都不种树(装上灯),则树数+1=间隔数.
03 典型例题
例题讲解
1.某房间里有四条腿的椅子和三条腿的凳子共16个,如果椅子腿数与凳子腿数的和为60条,有几张椅子和几条凳子?
【分析】本问题中涉及的等量关系有:
椅子数+凳子数=16,椅子腿数+凳子腿数=60.
解:设有x 张椅子,则有(16-x)条凳子.
根据题意,得4x+ 3(16-x)=60 .
解得 x = 12 .
凳子数为16-12=4(条).
答:有12张椅子,4条凳子.
例题讲解
2.王大伯3年前把手头一笔钱作为3年定期存款存入银行,年利率为5%.到期后得到本息共23000元,问当年王大伯存入银行多少钱?
解:设当年王大伯存入银行x元,年利率为5%,存期3年,所以3年的利息为3×5% x元.3年到期后本息共23000元.
根据题意,得 x +3×5% x =23000
解方程,得 x =20000
答:当年王大伯存入银行20000元.
例题讲解
3.小明与小红的家相距 20 km, 小明从家里出发骑自行车去小红家,两人商定小红到时候从家里出发骑自行车去接小明. 已知小明骑车的速度为13 km/h, 小红骑车的速度是 12 km/h.
(1) 如果两人同时出发,那么他们经过多少小时相遇?
(2) 如果小明先走 30 min,那么小红骑车要走多少小时才能与小明相遇?
例题讲解
解:(1) 设小明与小红骑车走了 x h 后相遇, 则根据等量关系,
得13x + 12x = 20 .解得 x = 0.8 .
(2) 设小红骑车走了 t h 后与小明相遇, 则根据等量关系, 得
13 ( 0.5+ t )+ 12t = 20 .解得 t = 0.54 .
答:(1)经过 0.8 h 他们两人相遇(2)小红骑车走 0.54 h 后与小明相遇.
4.选择
(1)甲、乙两人练习赛跑,甲每秒跑4米,乙每秒跑6米,甲先跑10秒,乙开始跑,设乙x秒后追上甲,依题意列方程得( )
A.6x =4x B. 6x=4x+40
C.6x= 4x-40 D. 4x+10=6x
B
A.12.5千米/时 B.15千米/时
C.17.5千米/时 D.20千米/时
(2)甲、乙两人骑自行车同时从相距65千米的两地相向而行,2小时相遇,若甲比乙每小时多骑2.5千米,则乙的时速是( )
B
例题讲解
5.填空
某商场把进价为1980元的商品按标价的八折出售,仍获利10%, 则该商品的标价为 元.
分析:
设标价为x元,按标价的八折出售为80%?x;按1980元出售获利80%x - 1980;根据题意可得80%?x-1980=10%×1980;解可得答案.
解答:
设标价为x元,
则依题意可列方程:80%?x - 1980=10%×1980;
解得x =2722.5.
2722.5
例题讲解
04 拓展提高
拓展提高
应用
1.某商场将某种商品按原价的8折出售,此时商品的利润率 10%。已知这种商品的进价为1800元,那么这种商品的原价是多少?
分析:利润率= = 。在解决这个问题的过程中,要抓住这个等量关系。由于本例中只提到售价、进价和利润率,因此我们可以用“进价”代替“成本”。
解这个方程,得 x =2475.
因此,这种商品的原价为2475元。
成本
售价-成本
解:设商品原价是x元,根据题意,得
拓展提高
应用
2.一队学生去校外进行军事野营训练,他们以5km/h的速度行进,走了18 min的时候,学校要将一个紧急通知传给队长,通讯员从学校出发,骑自行车以14 km/h的速度按原路追上去,通讯员用多少时间可以追上学生的队伍?
05 课堂小结
课堂小结
问题的已
知条件
解决行程问题的基本步骤:
画出线
段图
找出等
量关系
列方程
并求解
回答
同向追及问题
同地不同时:
同时不同地:
甲路程+路程差=乙路程;
甲路程=乙路程
相向相遇问题
甲的路程+乙的路程=总路程
重点理解行程问题
06 作业布置
作业布置
课后练习1、2题
谢 谢 观 看
同课章节目录
