人教版 数学 必修3 2.2.1 用样本估计总体(共16张ppt)
文档属性
| 名称 | 人教版 数学 必修3 2.2.1 用样本估计总体(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 280.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-15 10:10:20 | ||
图片预览




文档简介
课件16张PPT。复习旧知 引入新知做频率分布直方图的步骤1.求极差2.决定组据与组数3.将数据分组4.列频率分布表5.画频率分布直方图2.2.1用样本的频率分布估计总体分布第二课时学习目标 1.会作频率折线图并了解总体密度曲线的定义
2.掌握茎叶图的意义及画法,并能在实际问题中用
茎叶图用数据统计;
3.通过实例体会频率分布直方图、频率折线图、
茎叶图的各自特征,从而恰当的选择上述方法
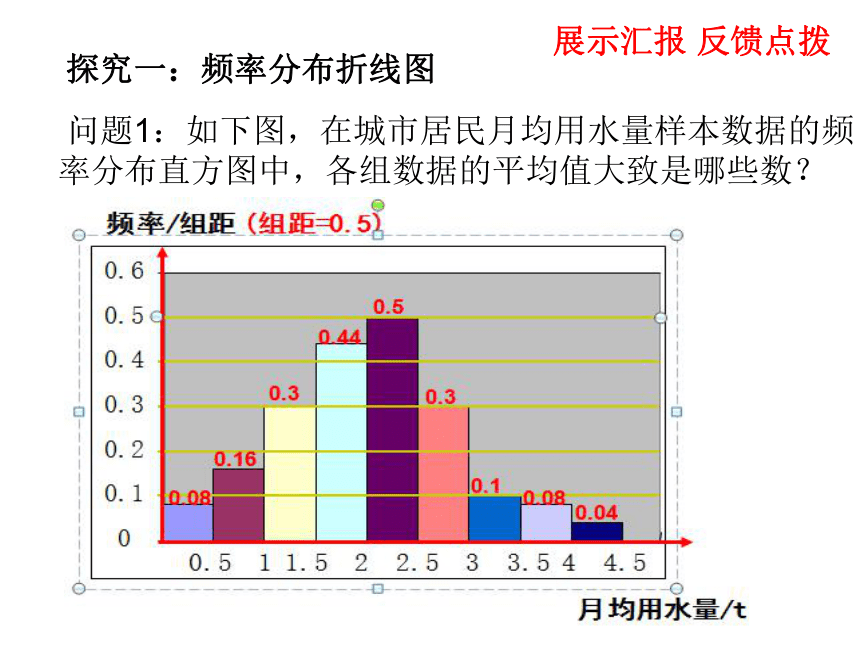
分析样本的分布,准确地做出总体估计。展示汇报 反馈点拨探究一:频率分布折线图 问题1:如下图,在城市居民月均用水量样本数据的频
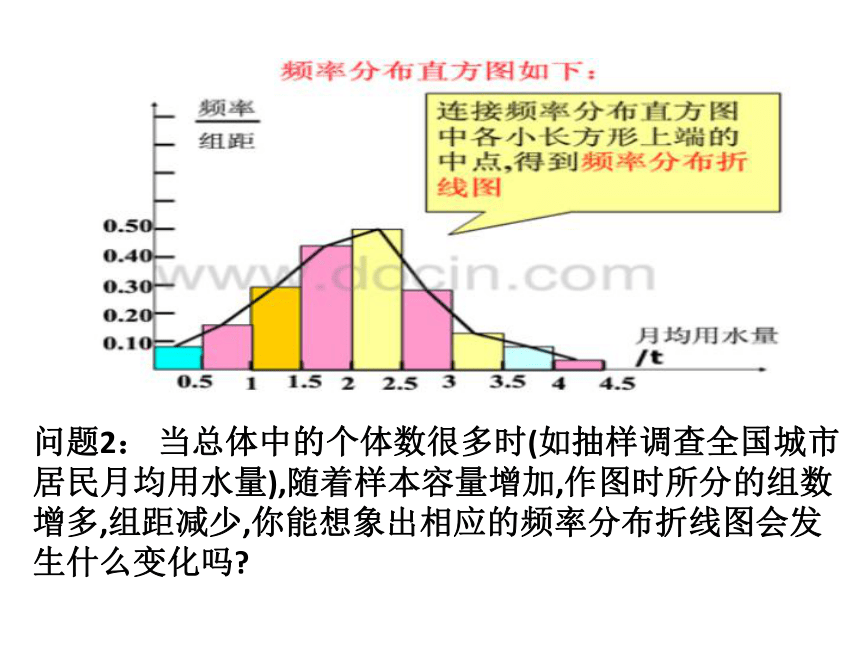
率分布直方图中,各组数据的平均值大致是哪些数?问题2: 当总体中的个体数很多时(如抽样调查全国城市
居民月均用水量),随着样本容量增加,作图时所分的组数
增多,组距减少,你能想象出相应的频率分布折线图会发
生什么变化吗?
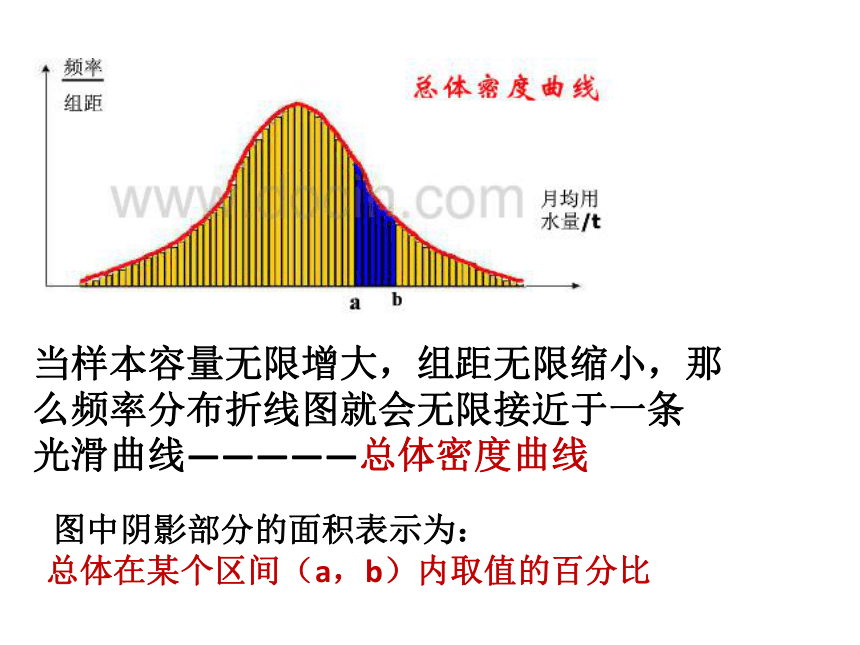
当样本容量无限增大,组距无限缩小,那
么频率分布折线图就会无限接近于一条
光滑曲线—————总体密度曲线图中阴影部分的面积表示为:总体在某个区间(a,b)内取值的百分比问题3: 对于一个总体,如果存在总体密度曲线,能否
通过样本数据准确地画出总体密度曲线?为什么?探究二:茎叶图某赛季甲、乙两名篮球运动员每场比赛的得分情况如下:
甲运动员得分:13,51,23,8,26,38,16,33,14,28,39;
乙运动员得分:49,24,12,31,50,31,44,36,15,37,25,36,39.请用适当的方法表示上述数据,并对两名运动员的得分能力进行比较. 问题一:用上次课所学的制作样本的频率分布直方图来分析好吗? 当数据比较少时应用频率分布直方图反而不方便 茎叶图:顾名思义,茎是指中间的一列数,叶就是从茎的旁边生长出来的数.中间的数字表示得分的十位数,旁边的数字分别表示两个人得分的个位数. 我们以下采用茎叶图来研究甲运动员得分:13,51,23,8,26,38,16,33,14,28,39;
乙运动员得分:49,24,12,31,50,31,44,36,15,37,25,36,39甲得分除一个特殊得分51分外,也大致对称分布,也是“
单峰”的,有9/11的叶主要集中在茎1、2、3上中位数是26. 乙得分基本上是对称的,叶的分布是“单峰”的,有10/13
的叶是分布在茎2、3、4上,中位数是36。问题二:和直方图比较,茎叶图有什么特点茎叶图不仅能保留原始数据而且能够展示数据的分布情况 。 由上表可以得出两名运动员的水平高低吗?从上述中位数的大小就可以看得出乙运动员的成绩更好.另外乙运动员的得分更集中于峰值附近这说明乙运动员的发挥更稳定. 问题三:通过上述的学习,请总结茎叶图的特点.
茎叶图的缺点是其分析只是粗略的对
差异不大的两组数据不易分析?表示三位 数以上的数据时不够方便.用茎叶图表示数据有两个突出的优点
一是所有的信息都可以从这个茎叶图上得到二是茎叶图便于记录和表示. 缺点:甲的得分:95,81,75,91,86,89,71,65,76,88,94,110,107;
乙的得分:83,86,93,99,88,103,98,114,98,79,101,88,110. 画出两人数学成绩的茎叶图,并根据茎叶图对两人的成绩进行比较例一:课堂小结 达标检测
1.频率分布折线图
2.总体密度曲线
3.茎叶图
下面一组数据是某生产车间30名工人某日加工零件的个数请设计适当的茎叶图表示这组数据?并由图出发说明一下这个车间此日的生产情况. 可以看出30名工人的日加工零件个数稳定在120件左右.某市对上、下班交通情况做抽样调查,上、下班时间各抽取了12辆机动车行驶时速如下,
上班时间30 33 18 27 32 40 26 28 21 28 35 20
下班时间27 19 32 29 36 29 30 22 25 16 17 30
请用茎叶图表示上面的样本数据并求出样本数据的中位数.
2.掌握茎叶图的意义及画法,并能在实际问题中用
茎叶图用数据统计;
3.通过实例体会频率分布直方图、频率折线图、
茎叶图的各自特征,从而恰当的选择上述方法
分析样本的分布,准确地做出总体估计。展示汇报 反馈点拨探究一:频率分布折线图 问题1:如下图,在城市居民月均用水量样本数据的频
率分布直方图中,各组数据的平均值大致是哪些数?问题2: 当总体中的个体数很多时(如抽样调查全国城市
居民月均用水量),随着样本容量增加,作图时所分的组数
增多,组距减少,你能想象出相应的频率分布折线图会发
生什么变化吗?
当样本容量无限增大,组距无限缩小,那
么频率分布折线图就会无限接近于一条
光滑曲线—————总体密度曲线图中阴影部分的面积表示为:总体在某个区间(a,b)内取值的百分比问题3: 对于一个总体,如果存在总体密度曲线,能否
通过样本数据准确地画出总体密度曲线?为什么?探究二:茎叶图某赛季甲、乙两名篮球运动员每场比赛的得分情况如下:
甲运动员得分:13,51,23,8,26,38,16,33,14,28,39;
乙运动员得分:49,24,12,31,50,31,44,36,15,37,25,36,39.请用适当的方法表示上述数据,并对两名运动员的得分能力进行比较. 问题一:用上次课所学的制作样本的频率分布直方图来分析好吗? 当数据比较少时应用频率分布直方图反而不方便 茎叶图:顾名思义,茎是指中间的一列数,叶就是从茎的旁边生长出来的数.中间的数字表示得分的十位数,旁边的数字分别表示两个人得分的个位数. 我们以下采用茎叶图来研究甲运动员得分:13,51,23,8,26,38,16,33,14,28,39;
乙运动员得分:49,24,12,31,50,31,44,36,15,37,25,36,39甲得分除一个特殊得分51分外,也大致对称分布,也是“
单峰”的,有9/11的叶主要集中在茎1、2、3上中位数是26. 乙得分基本上是对称的,叶的分布是“单峰”的,有10/13
的叶是分布在茎2、3、4上,中位数是36。问题二:和直方图比较,茎叶图有什么特点茎叶图不仅能保留原始数据而且能够展示数据的分布情况 。 由上表可以得出两名运动员的水平高低吗?从上述中位数的大小就可以看得出乙运动员的成绩更好.另外乙运动员的得分更集中于峰值附近这说明乙运动员的发挥更稳定. 问题三:通过上述的学习,请总结茎叶图的特点.
茎叶图的缺点是其分析只是粗略的对
差异不大的两组数据不易分析?表示三位 数以上的数据时不够方便.用茎叶图表示数据有两个突出的优点
一是所有的信息都可以从这个茎叶图上得到二是茎叶图便于记录和表示. 缺点:甲的得分:95,81,75,91,86,89,71,65,76,88,94,110,107;
乙的得分:83,86,93,99,88,103,98,114,98,79,101,88,110. 画出两人数学成绩的茎叶图,并根据茎叶图对两人的成绩进行比较例一:课堂小结 达标检测
1.频率分布折线图
2.总体密度曲线
3.茎叶图
下面一组数据是某生产车间30名工人某日加工零件的个数请设计适当的茎叶图表示这组数据?并由图出发说明一下这个车间此日的生产情况. 可以看出30名工人的日加工零件个数稳定在120件左右.某市对上、下班交通情况做抽样调查,上、下班时间各抽取了12辆机动车行驶时速如下,
上班时间30 33 18 27 32 40 26 28 21 28 35 20
下班时间27 19 32 29 36 29 30 22 25 16 17 30
请用茎叶图表示上面的样本数据并求出样本数据的中位数.
