湘教版七年级数学上册第2章 代数式2.5 整式的加法和减法整式教学课件(共36张)
文档属性
| 名称 | 湘教版七年级数学上册第2章 代数式2.5 整式的加法和减法整式教学课件(共36张) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 00:00:00 | ||
图片预览











文档简介
(共36张PPT)
整式的加法和减法
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
如果有一罐硬币(分别为一角、五角、一元的),你会如何去数呢?
同学们是否是这样想的呢?还有什么其他的办法吗?
02 新知探究
新知探究
同类项概念
同类项:多项式中,所含字母相同,并且相同字母的指数也分别相同的项叫做同类项.
(1)两个相同:字母相同、相同字母的指数相同;
(2)两个无关:与系数大小无关;与字母顺序无关;
(3)所有的常数项都是同类项.
说明:
新知探究
(3)-3pq与3qp
(1)2x2y与-3x2y
(2)2abc与2ab
(4) -4x2y与5xy2
先判断以下每一组是否为同类项,若不是,请为前者配一个.
√
√
3abc
x2y
×
×
练一练
新知探究
小归纳
(1)同类项只与字母及其指数有关,与系数无关,与字母在单项式中的排列顺序无关;
(2)抓住“两个相同”:一是所含的字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可.
(3)不要忘记几个单独的数也是同类项.
同类项的判别方法
新知探究
练一练
(1)如果2a2bn+1与-4amb3是同类项,则m= ,n= .
(2)在6xy-3x2-4x2y-5yx2+x2中没有同类项的项是 .
2
2
6xy
分析:(1)根据同类项的定义,可知a的指数相同,b的指数也相同,即m=2,n+1=3.
新知探究
合并同类项
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三合,将同一括号内的同类项相加即可.
系数相加,字母及其指数不变
新知探究
练一练
(1)a+a=2a
(2)3a+2b=5ab
(3)5y2-3y2=2
讨论一下下列合并同类项是否正确,并说明理由。
(4)4x2y-5xy2=-x2y
(5)3x2+2x3=5x5
(6)a+a-5a=-3a
×
√
×
×
×
√
新知探究
去括号
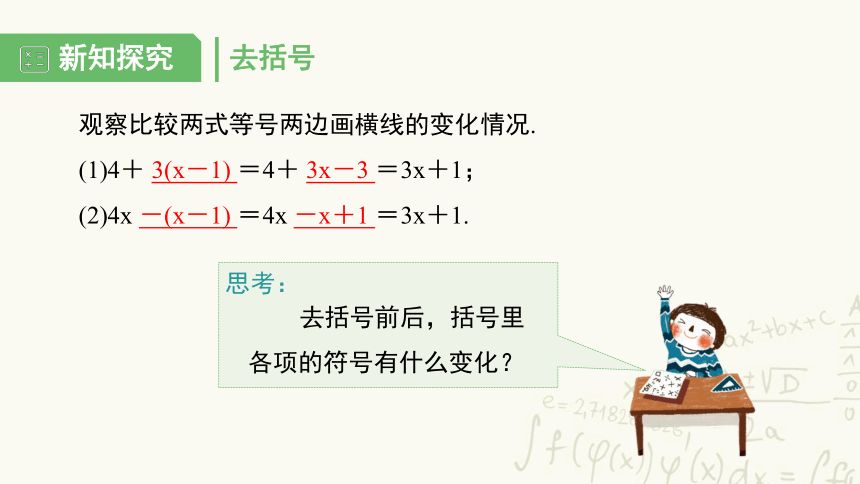
观察比较两式等号两边画横线的变化情况.
(1)4+ 3(x-1) =4+ 3x-3 =3x+1;
(2)4x -(x-1) =4x -x+1 =3x+1.
去括号前后,括号里各项的符号有什么变化?
思考:
新知探究
想一想
括号前是“+”号,把括号和它前面的“+”号去掉后,原括号里各项的符号都不改变;
括号前是“-”号,把括号和它前面的“-”号去掉后,原括号里各项的符号都要改变.
去括号法则:
新知探究
判断正误
(2)-3(x-8)=-3x-24
(4)-2(6-x)=-12+2x
(3)4(-3-2x)=-12+8x
错
=3x+3×8
错因:分配律,漏乘3.
错
=-3x+24
错因:括号前面是负数,去掉负号和括号后每一项都变号.
对
错
错因:括号前面是正数,去掉正号和括号后每一项都不变号.
=-12-8x
(1)3(x+8)=3x+8
新知探究
小归纳
【归纳总结】
(1)去括号时,不仅要去掉括号,还要连同括号前面的符号一起去掉.
(2)去括号时,首先要弄清括号前是“+”号还是“-”号.
(3)注意法则中的“都”字,变号时,各项都变号;不变号时,各项都不变号.
(4)当括号前有数字因数时,应运用乘法分配律运算,切勿漏乘.
(5)出现多层括号时,一般是由里向外逐层去括号.
新知探究
想一想
原三位数728,百位与个位交换后的数为827,由728 -827= -99.你能看出什么规律并验证它吗?
解析:设原三位数为100a+10b+c,百位与个位交换后的数为100c+10b+a,它们的差为:
(100a+10b+c)-( 100c+10b+a)
= 100a+10b+c-100c-10b-a
=99a-99c
=99(a-c)
任意一个三位数可以表示成100a+10b+c
新知探究
在上面的问题中,涉及了整式的那种运算?说说你是如何运算的?
去括号、合并同类项
八字诀
整式的加减运算
说一说
新知探究
练一练
求整式 与 的和.
有括号要先去括号
有同类项再合并同类项
结果中不能再有同类项
新知探究
练一练
解:根据题意,得
求多项式 与多项式 的和与差.
去括号
合并同类项
去括号
合并同类项
03 典型例题
例题讲解
1.合并下式中的同类项:
(1) (2)
(1)
解析:
(2)
例题讲解
2.火车站和飞机场都为旅客提供“打包” 服务,如果长、宽、 高分别为x,y,z米的箱子 按如图所示的方式 “打包 ”, 至少需要多少米的“打包”带?
(其中红色线为“打包”带)
z
x
y
2(x+z)+
2(z + y)
2?
2x+4y+6z
解析: 根据示意图所显示,总共需要的打包带为_______________,合并同类项后,至少需要___________米的“打包 ” 带.
“至少”意即“带子”长最短.
例题讲解
分析:先去括号,然后合并同类项,最后代入求值
解:
将
代入
中,得出最终结果为-3.
3.先化简,再求值:,其中
(1)下列各组式子中是同类项的是( )
A.-2a与a2 B.2a2b与3ab2
C.5ab2c与-b2ac D.-ab2和4ab2c
(2)下列运算中正确的是( )
A.3a2-2a2=a2 B.3a2-2a2=1
C.3x2-x2=3 D.3x2-x=2x
C
A
4.选择
例题讲解
5.填空
(1)如果5x2y与xmyn是同类项,那么 m=____,n=____.
(2)合并同类项:
(1)-a-a-2a=________.
(2)-xy-5xy+6yx=________.
(3)0.8ab2-a2b+0.2ab2=_______.
2
-4a
0
ab2-a2b
1
例题讲解
6.化简下列各式:
(1)8m+2n+(5m-n); (2)(5p-3q)-3( ).
例题讲解
(1)8m+2n+(5m-n)
=8m+2n+(5m-n)
=13m + n
04 拓展提高
拓展提高
1. 一天,王村的小明奶奶提着一篮子土豆去换苹果,双方商定的结果是:1千克土豆换0.5千克苹果.当称完土豆和篮子的重量后,摊主对小明奶奶说:“别称篮子的重量了,称苹果时也带篮子称,这样既省事又互不吃亏.”你认为摊主的话有道理吗?请你用所学的有关数学知识加以判定.
解:设土豆重a千克,篮子重b千克,则应换苹果0.5a千克.若不称篮子,则实换苹果为 0.5a+0.5b-b=(0.5a-0.5b)千克,很明显小明奶奶少得苹果0.5b千克。所以摊主说得没有道理,这样做小明奶奶吃亏了.
拓展提高
3x+2y+z
2.某花店一枝黄色康乃馨的价格是x元,一枝红色玫瑰的价格是y元,一枝白色百合花的价格是z元,下面这三束鲜花的价格各是多少?这三束鲜花的总价是多少元?
2x+2y+3z
4x+3y+2z
这三束鲜花的总价是:
3x+2y+z +
2x+2y+3z +
答: 三束鲜花的价格各是:
4x+3y+2z
=
9x+7y+6z .
拓展提高
3.两船从同一港口出发反向而行,甲船顺水,乙船逆水,两船在静水中速度都是50千米/时,水流速度是a千米/时.
问: (1)2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?
解:顺水速度=船速+水速=(50+a)km/h, 逆水速度=船速-水速=(50-a)km/h.
(1) 2小时后两船相距(单位:km)
2(50+a)+2(50-a)=100+2a+100-2a=200.
(2) 2小时后甲船比乙船多航行(单位:km)
2(50+a)-2(50-a)=100+2a-100+2a=4a.
05 课堂小结
课堂小结
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
1.整式加减的作用是把整式化简,化简方法就是去括号,合并同类项.
2.遇有多层括号时,一般先去小括号,再去中括号,最后去大括号.
3.如果遇到数与多项式相乘,要运用乘法分配律计算.
4.在做化简求值题时,要注意格式.
课堂小结
整式加减的步骤
整式加减的应用
整式的加减
?去括号
?合并同类项
06 作业布置
作业布置
1、课后习题 1、2
2、预习新课习题
谢 谢 观 看
整式的加法和减法
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
如果有一罐硬币(分别为一角、五角、一元的),你会如何去数呢?
同学们是否是这样想的呢?还有什么其他的办法吗?
02 新知探究
新知探究
同类项概念
同类项:多项式中,所含字母相同,并且相同字母的指数也分别相同的项叫做同类项.
(1)两个相同:字母相同、相同字母的指数相同;
(2)两个无关:与系数大小无关;与字母顺序无关;
(3)所有的常数项都是同类项.
说明:
新知探究
(3)-3pq与3qp
(1)2x2y与-3x2y
(2)2abc与2ab
(4) -4x2y与5xy2
先判断以下每一组是否为同类项,若不是,请为前者配一个.
√
√
3abc
x2y
×
×
练一练
新知探究
小归纳
(1)同类项只与字母及其指数有关,与系数无关,与字母在单项式中的排列顺序无关;
(2)抓住“两个相同”:一是所含的字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可.
(3)不要忘记几个单独的数也是同类项.
同类项的判别方法
新知探究
练一练
(1)如果2a2bn+1与-4amb3是同类项,则m= ,n= .
(2)在6xy-3x2-4x2y-5yx2+x2中没有同类项的项是 .
2
2
6xy
分析:(1)根据同类项的定义,可知a的指数相同,b的指数也相同,即m=2,n+1=3.
新知探究
合并同类项
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三合,将同一括号内的同类项相加即可.
系数相加,字母及其指数不变
新知探究
练一练
(1)a+a=2a
(2)3a+2b=5ab
(3)5y2-3y2=2
讨论一下下列合并同类项是否正确,并说明理由。
(4)4x2y-5xy2=-x2y
(5)3x2+2x3=5x5
(6)a+a-5a=-3a
×
√
×
×
×
√
新知探究
去括号
观察比较两式等号两边画横线的变化情况.
(1)4+ 3(x-1) =4+ 3x-3 =3x+1;
(2)4x -(x-1) =4x -x+1 =3x+1.
去括号前后,括号里各项的符号有什么变化?
思考:
新知探究
想一想
括号前是“+”号,把括号和它前面的“+”号去掉后,原括号里各项的符号都不改变;
括号前是“-”号,把括号和它前面的“-”号去掉后,原括号里各项的符号都要改变.
去括号法则:
新知探究
判断正误
(2)-3(x-8)=-3x-24
(4)-2(6-x)=-12+2x
(3)4(-3-2x)=-12+8x
错
=3x+3×8
错因:分配律,漏乘3.
错
=-3x+24
错因:括号前面是负数,去掉负号和括号后每一项都变号.
对
错
错因:括号前面是正数,去掉正号和括号后每一项都不变号.
=-12-8x
(1)3(x+8)=3x+8
新知探究
小归纳
【归纳总结】
(1)去括号时,不仅要去掉括号,还要连同括号前面的符号一起去掉.
(2)去括号时,首先要弄清括号前是“+”号还是“-”号.
(3)注意法则中的“都”字,变号时,各项都变号;不变号时,各项都不变号.
(4)当括号前有数字因数时,应运用乘法分配律运算,切勿漏乘.
(5)出现多层括号时,一般是由里向外逐层去括号.
新知探究
想一想
原三位数728,百位与个位交换后的数为827,由728 -827= -99.你能看出什么规律并验证它吗?
解析:设原三位数为100a+10b+c,百位与个位交换后的数为100c+10b+a,它们的差为:
(100a+10b+c)-( 100c+10b+a)
= 100a+10b+c-100c-10b-a
=99a-99c
=99(a-c)
任意一个三位数可以表示成100a+10b+c
新知探究
在上面的问题中,涉及了整式的那种运算?说说你是如何运算的?
去括号、合并同类项
八字诀
整式的加减运算
说一说
新知探究
练一练
求整式 与 的和.
有括号要先去括号
有同类项再合并同类项
结果中不能再有同类项
新知探究
练一练
解:根据题意,得
求多项式 与多项式 的和与差.
去括号
合并同类项
去括号
合并同类项
03 典型例题
例题讲解
1.合并下式中的同类项:
(1) (2)
(1)
解析:
(2)
例题讲解
2.火车站和飞机场都为旅客提供“打包” 服务,如果长、宽、 高分别为x,y,z米的箱子 按如图所示的方式 “打包 ”, 至少需要多少米的“打包”带?
(其中红色线为“打包”带)
z
x
y
2(x+z)+
2(z + y)
2?
2x+4y+6z
解析: 根据示意图所显示,总共需要的打包带为_______________,合并同类项后,至少需要___________米的“打包 ” 带.
“至少”意即“带子”长最短.
例题讲解
分析:先去括号,然后合并同类项,最后代入求值
解:
将
代入
中,得出最终结果为-3.
3.先化简,再求值:,其中
(1)下列各组式子中是同类项的是( )
A.-2a与a2 B.2a2b与3ab2
C.5ab2c与-b2ac D.-ab2和4ab2c
(2)下列运算中正确的是( )
A.3a2-2a2=a2 B.3a2-2a2=1
C.3x2-x2=3 D.3x2-x=2x
C
A
4.选择
例题讲解
5.填空
(1)如果5x2y与xmyn是同类项,那么 m=____,n=____.
(2)合并同类项:
(1)-a-a-2a=________.
(2)-xy-5xy+6yx=________.
(3)0.8ab2-a2b+0.2ab2=_______.
2
-4a
0
ab2-a2b
1
例题讲解
6.化简下列各式:
(1)8m+2n+(5m-n); (2)(5p-3q)-3( ).
例题讲解
(1)8m+2n+(5m-n)
=8m+2n+(5m-n)
=13m + n
04 拓展提高
拓展提高
1. 一天,王村的小明奶奶提着一篮子土豆去换苹果,双方商定的结果是:1千克土豆换0.5千克苹果.当称完土豆和篮子的重量后,摊主对小明奶奶说:“别称篮子的重量了,称苹果时也带篮子称,这样既省事又互不吃亏.”你认为摊主的话有道理吗?请你用所学的有关数学知识加以判定.
解:设土豆重a千克,篮子重b千克,则应换苹果0.5a千克.若不称篮子,则实换苹果为 0.5a+0.5b-b=(0.5a-0.5b)千克,很明显小明奶奶少得苹果0.5b千克。所以摊主说得没有道理,这样做小明奶奶吃亏了.
拓展提高
3x+2y+z
2.某花店一枝黄色康乃馨的价格是x元,一枝红色玫瑰的价格是y元,一枝白色百合花的价格是z元,下面这三束鲜花的价格各是多少?这三束鲜花的总价是多少元?
2x+2y+3z
4x+3y+2z
这三束鲜花的总价是:
3x+2y+z +
2x+2y+3z +
答: 三束鲜花的价格各是:
4x+3y+2z
=
9x+7y+6z .
拓展提高
3.两船从同一港口出发反向而行,甲船顺水,乙船逆水,两船在静水中速度都是50千米/时,水流速度是a千米/时.
问: (1)2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?
解:顺水速度=船速+水速=(50+a)km/h, 逆水速度=船速-水速=(50-a)km/h.
(1) 2小时后两船相距(单位:km)
2(50+a)+2(50-a)=100+2a+100-2a=200.
(2) 2小时后甲船比乙船多航行(单位:km)
2(50+a)-2(50-a)=100+2a-100+2a=4a.
05 课堂小结
课堂小结
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
1.整式加减的作用是把整式化简,化简方法就是去括号,合并同类项.
2.遇有多层括号时,一般先去小括号,再去中括号,最后去大括号.
3.如果遇到数与多项式相乘,要运用乘法分配律计算.
4.在做化简求值题时,要注意格式.
课堂小结
整式加减的步骤
整式加减的应用
整式的加减
?去括号
?合并同类项
06 作业布置
作业布置
1、课后习题 1、2
2、预习新课习题
谢 谢 观 看
同课章节目录
