湘教版七年级数学上册第1章 有理数1.6 有理数的乘方教学课件(共32张)
文档属性
| 名称 | 湘教版七年级数学上册第1章 有理数1.6 有理数的乘方教学课件(共32张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 00:00:00 | ||
图片预览











文档简介
(共32张PPT)
有理数的乘方
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
读一读 0.1的学问
下图是日本某小学门前贴的一张海报,你懂其中的含义吗?
新课导入
读一读
事实上,图中所展示给我们的信息其实很简单,那便是:每天进步一点点,总有一天能够变成巨大的力量.反之,稍微有一点怠慢的话,总有一天会变得无力.
如何用数学关系来解释呢?
02 新知探究
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
新知探究
乘方概念
这种求n个相同因数的乘积的运算叫做乘方,乘方的结果叫做幂.
1次方可省略不写,2次方又叫平方,3次方又叫立方
a×a×……×a = an
n个
幂
指数
因数的个数
底数
因数
新知探究
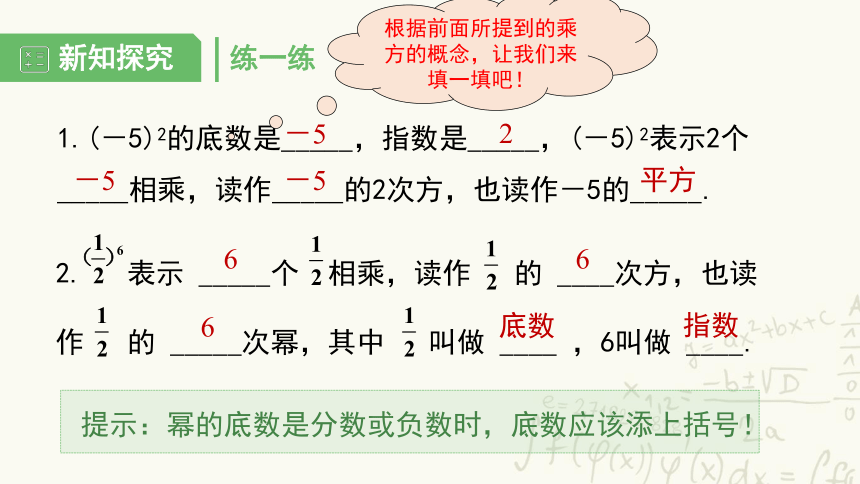
练一练
1.(-5)2的底数是_____,指数是_____,(-5)2表示2个 _____相乘,读作_____的2次方,也读作-5的_____.
2. 表示 _____个 相乘,读作 的 ____次方,也读作 的 _____次幂,其中 叫做 ____ ,6叫做 ____.
6
2
-5
-5
平方
-5
6
6
底数
指数
提示:幂的底数是分数或负数时,底数应该添上括号!
根据前面所提到的乘方的概念,让我们来填一填吧!
新知探究
(-3)2 -32
(-3)2与-32有什么不同?结果相等吗?
无括号
3的平方的相反数
2个(-3)相乘
即(-3)×(-3)
2个3相乘的积的相反数
即-(3×3)
-9
9
有括号
-3的平方
写法
读法
意义
结果
议一议
注意:底数是负数或分数时,必须加上括号.
新知探究
练一练
你能计算出下列各个有理数的结果吗?
(1); (2); (3); (4)
解 (1) =(-3)(-3) (-3)= -27
(2) = 0 0 0 0 0 0 0 = 0
(3) = =
(4) = =
新知探究
负数的奇次幂是负数,负数的偶次幂是正数.
正数的任何正整数次幂都是正数.
根据有理数的乘法法则可以得出:
0的任何正整数次幂都是0.
归纳总结
新知探究
动脑筋
快速计算下面几道题:
(1)13 (2)12018 (3)(-1)8
(4)(-1)2018 (5)(-1)7 (6)(-1)2019
=1
=1
=1
=1
=-1
=-1
思考:你发现了什么规律呢?
新知探究
想一想
(1)1的任何正整数次幂都为 ;
(2)-1的幂很有规律:
-1的奇次幂是 ,-1的偶次幂是 .
注意:当底数是负数或分数时,底数一定要加上括弧,这也是辨认底数的方法.
1
-1
1
新知探究
科学记数法概念
科学记数法:把一个绝对值大于 10 的数记做 a×的形式,其中 a 是整数数位只有一位的数(即 1≤|a|<10),这种记数法叫做科学记数法。
新知探究
练一练
用科学记数法表示下列各数:
(1) 315 000 000; (2) -2 180 000 000.
解析:
(1)3.15×108 (2)-2.18×109
03 典型例题
例题讲解
1.计算:
(-2)3; (2) 08;
( )4; (4)(- )3
解析:
(1)(-2)3 =(-2)×(-2)×(-2)=-8;
(2) 08 = 0×0×0×0×0×0×0×0=0
(3)(2/5)4= 2/5×2/5×2/5×2/5= 16/625 ;
(4)(- )3=(- )×(- )×(- )= -1/8
例题讲解
2.计算:
(1)(-4)2 ×(-1/2)2;
(2) - 23 × ( - 2 )2
解析:
(1) (-4)2 ×(-1/2)2= 1 6 × 1/4= 4 ;
(2) -23×(-2)2 = -8 × 4 = -32 .
例题讲解
3.用科学记数法表示下列各数:
(1) 108 000 000; (2) - 32 000 000
解析:
(1) 108 000 000= 1.08 × 108
(2) -32 000 000= - 3.2 × 107
拓展提高
应用
4.2010年11月14日,半年评选一次的全球超级计算机500强名单正式公布,我国“天河一号”超级计算机以每秒2570万亿次的实测运算速度,成为世界运算最快的超级计算机.请用科学记数法表示”天河一号” 的实测运算速度为每秒多少次.
拓展提高
应用
解析:
2570万亿就是 2 570 000 000 000 000.
用科学记数法表示为2.57× , 即 “天河一号”的实测运算速度为每秒2.57×次
∴ b=2, a= -1
∴ ab=1
5.一个有理数的平方是正数,那么这个有理数的立方是( )
A. 正数 B .负数 C .正数或负数 D. 整数
6.已知 b-2 ︳与 (a+1)2 互为相反数,求ab 的值.
解:∵ ,,且两者互为相反数
b-2
b-2
=0 , ( a+1)2
=
0
∴
C
例题讲解
例题讲解
(7)= .
(1)-(-3)2= ; (2)-32= ;
(3)(-5)3= ; (4)0.13= ;
(5)(-1)9= ; (6)(-1)12= ;
-9
-9
-125
0.001
-1
1
7.填空
(4)(-4)3÷(-1)200+2×(-3)4=-64÷1+2×81=98
(1) ; (2)-23×(-32)
(3)64÷(-2)5 ; (4)(-4)3÷(-1)200+2×(-3)4
(2)-23×(-32)=-8×(-9)=72;
(3)64÷(-2)5=64÷(-32)=-2;
8.计算
例题讲解
04 拓展提高
拓展提高
应用
如果 x-3 +(y+2)2=0,求yx的值.
且 |x-3| +(y+2)2=0,
解:∵ |x-3| ≥0,(y+2)2≥0
∴ |x-3| =0,(y+2)2=0,
∴x=3, y=-2,
∴=(-2)3= -8.
方法总结:几个非负数的和为0,则这几个数都等于0.
05 课堂小结
课堂小结
1.求几个相同因数的积的运算,叫做乘方.
幂
指数
底数
课堂小结
2.乘方法则:正数的任何次幂都是正数;
负数的奇次幂是负数,负数的偶次幂是正数;
0的任何次幂(0次幂除外)都为0.
3.科学记数法:把一个绝对值大于10的数记做a×的形式,其中a是整数数位只有一位的数(即 1≤|a|<10),这种记数法叫做科学记数法.
06 作业布置
作业布置
练习:1、P44第1、2题
2、预习新课
谢 谢 观 看
有理数的乘方
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
读一读 0.1的学问
下图是日本某小学门前贴的一张海报,你懂其中的含义吗?
新课导入
读一读
事实上,图中所展示给我们的信息其实很简单,那便是:每天进步一点点,总有一天能够变成巨大的力量.反之,稍微有一点怠慢的话,总有一天会变得无力.
如何用数学关系来解释呢?
02 新知探究
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
新知探究
乘方概念
这种求n个相同因数的乘积的运算叫做乘方,乘方的结果叫做幂.
1次方可省略不写,2次方又叫平方,3次方又叫立方
a×a×……×a = an
n个
幂
指数
因数的个数
底数
因数
新知探究
练一练
1.(-5)2的底数是_____,指数是_____,(-5)2表示2个 _____相乘,读作_____的2次方,也读作-5的_____.
2. 表示 _____个 相乘,读作 的 ____次方,也读作 的 _____次幂,其中 叫做 ____ ,6叫做 ____.
6
2
-5
-5
平方
-5
6
6
底数
指数
提示:幂的底数是分数或负数时,底数应该添上括号!
根据前面所提到的乘方的概念,让我们来填一填吧!
新知探究
(-3)2 -32
(-3)2与-32有什么不同?结果相等吗?
无括号
3的平方的相反数
2个(-3)相乘
即(-3)×(-3)
2个3相乘的积的相反数
即-(3×3)
-9
9
有括号
-3的平方
写法
读法
意义
结果
议一议
注意:底数是负数或分数时,必须加上括号.
新知探究
练一练
你能计算出下列各个有理数的结果吗?
(1); (2); (3); (4)
解 (1) =(-3)(-3) (-3)= -27
(2) = 0 0 0 0 0 0 0 = 0
(3) = =
(4) = =
新知探究
负数的奇次幂是负数,负数的偶次幂是正数.
正数的任何正整数次幂都是正数.
根据有理数的乘法法则可以得出:
0的任何正整数次幂都是0.
归纳总结
新知探究
动脑筋
快速计算下面几道题:
(1)13 (2)12018 (3)(-1)8
(4)(-1)2018 (5)(-1)7 (6)(-1)2019
=1
=1
=1
=1
=-1
=-1
思考:你发现了什么规律呢?
新知探究
想一想
(1)1的任何正整数次幂都为 ;
(2)-1的幂很有规律:
-1的奇次幂是 ,-1的偶次幂是 .
注意:当底数是负数或分数时,底数一定要加上括弧,这也是辨认底数的方法.
1
-1
1
新知探究
科学记数法概念
科学记数法:把一个绝对值大于 10 的数记做 a×的形式,其中 a 是整数数位只有一位的数(即 1≤|a|<10),这种记数法叫做科学记数法。
新知探究
练一练
用科学记数法表示下列各数:
(1) 315 000 000; (2) -2 180 000 000.
解析:
(1)3.15×108 (2)-2.18×109
03 典型例题
例题讲解
1.计算:
(-2)3; (2) 08;
( )4; (4)(- )3
解析:
(1)(-2)3 =(-2)×(-2)×(-2)=-8;
(2) 08 = 0×0×0×0×0×0×0×0=0
(3)(2/5)4= 2/5×2/5×2/5×2/5= 16/625 ;
(4)(- )3=(- )×(- )×(- )= -1/8
例题讲解
2.计算:
(1)(-4)2 ×(-1/2)2;
(2) - 23 × ( - 2 )2
解析:
(1) (-4)2 ×(-1/2)2= 1 6 × 1/4= 4 ;
(2) -23×(-2)2 = -8 × 4 = -32 .
例题讲解
3.用科学记数法表示下列各数:
(1) 108 000 000; (2) - 32 000 000
解析:
(1) 108 000 000= 1.08 × 108
(2) -32 000 000= - 3.2 × 107
拓展提高
应用
4.2010年11月14日,半年评选一次的全球超级计算机500强名单正式公布,我国“天河一号”超级计算机以每秒2570万亿次的实测运算速度,成为世界运算最快的超级计算机.请用科学记数法表示”天河一号” 的实测运算速度为每秒多少次.
拓展提高
应用
解析:
2570万亿就是 2 570 000 000 000 000.
用科学记数法表示为2.57× , 即 “天河一号”的实测运算速度为每秒2.57×次
∴ b=2, a= -1
∴ ab=1
5.一个有理数的平方是正数,那么这个有理数的立方是( )
A. 正数 B .负数 C .正数或负数 D. 整数
6.已知 b-2 ︳与 (a+1)2 互为相反数,求ab 的值.
解:∵ ,,且两者互为相反数
b-2
b-2
=0 , ( a+1)2
=
0
∴
C
例题讲解
例题讲解
(7)= .
(1)-(-3)2= ; (2)-32= ;
(3)(-5)3= ; (4)0.13= ;
(5)(-1)9= ; (6)(-1)12= ;
-9
-9
-125
0.001
-1
1
7.填空
(4)(-4)3÷(-1)200+2×(-3)4=-64÷1+2×81=98
(1) ; (2)-23×(-32)
(3)64÷(-2)5 ; (4)(-4)3÷(-1)200+2×(-3)4
(2)-23×(-32)=-8×(-9)=72;
(3)64÷(-2)5=64÷(-32)=-2;
8.计算
例题讲解
04 拓展提高
拓展提高
应用
如果 x-3 +(y+2)2=0,求yx的值.
且 |x-3| +(y+2)2=0,
解:∵ |x-3| ≥0,(y+2)2≥0
∴ |x-3| =0,(y+2)2=0,
∴x=3, y=-2,
∴=(-2)3= -8.
方法总结:几个非负数的和为0,则这几个数都等于0.
05 课堂小结
课堂小结
1.求几个相同因数的积的运算,叫做乘方.
幂
指数
底数
课堂小结
2.乘方法则:正数的任何次幂都是正数;
负数的奇次幂是负数,负数的偶次幂是正数;
0的任何次幂(0次幂除外)都为0.
3.科学记数法:把一个绝对值大于10的数记做a×的形式,其中a是整数数位只有一位的数(即 1≤|a|<10),这种记数法叫做科学记数法.
06 作业布置
作业布置
练习:1、P44第1、2题
2、预习新课
谢 谢 观 看
同课章节目录
