湘教版七年级数学上册第1章 有理数1.5.1 有理数的乘法教学课件(共32张)
文档属性
| 名称 | 湘教版七年级数学上册第1章 有理数1.5.1 有理数的乘法教学课件(共32张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
有理数的乘法
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
1、如果蜗牛从0处一直以每分钟2cm的速度向右爬行(规定:向右为正)那么3分钟后蜗牛在什么位置?
-2
0
2
4
6
8
2 + 2 + 2 = 6
新课导入
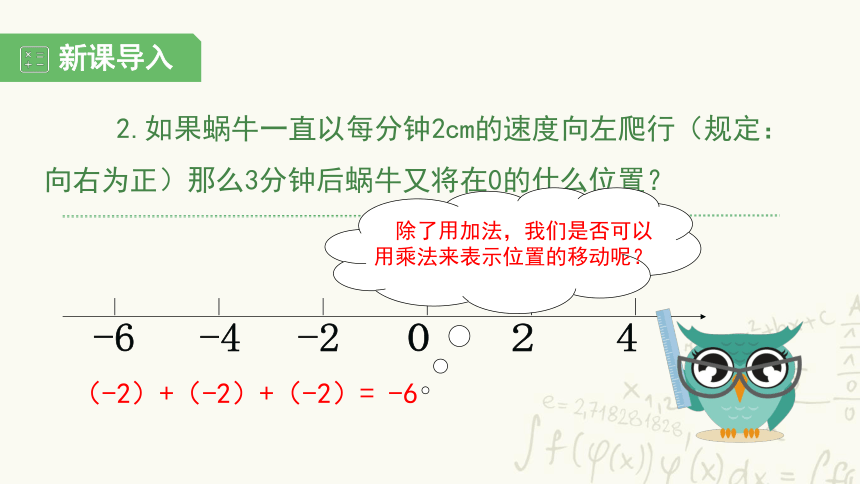
2.如果蜗牛一直以每分钟2cm的速度向左爬行(规定:向右为正)那么3分钟后蜗牛又将在0的什么位置?
-6
-4
-2
0
2
4
(-2)+(-2)+(-2)= -6
除了用加法,我们是否可以用乘法来表示位置的移动呢?
02 新知探究
新知探究
想一想
甲水库的水位每天升高3cm,乙水库的水位每天下降3cm,如果规定上升为正,下降为负,4天后,甲、乙水库水位的总变化量是多少?
我们是不是可以得出这样的算式:
3+3+3+3=3×4=12,
(-3)+(-3)+(-3)+(-3)=(-3)× 4 = -12
新知探究
想一想
(?3)×0 =_____.
0
(?3)×4=(?3)+(?3)+(?3)+(?3) =?12
(?3)×3 = _____________=_____,
(?3)×2 =_____________=_____,
(?3)×1 =_____,
?9
?6
类比前面得到的式子,能否将下面的空填好呢?
(?3)+(?3)+(?3)
(?3)+(?3)
3×4=3+3+3+3 = 12
?3
新知探究
乘法概念学习
如图,一只蜗牛沿直线L爬行,它现在的位置在L上的点O.
O
1.如果一只蜗牛向右爬行2cm记为+2cm,那么向左爬行2cm应该记为 .
2.如果3分钟以后记为+3分钟,那么3分钟以前应该记为__________.
-2cm
-3分钟
新知探究
规定:向左为负,向右为正.现在前为负,现在后为正.
结果:3分钟后在L上点O 边 cm处
表示: .
(+2)×(+3)= 6
(1)如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置?
O
2
6
4
l
乘法概念学习
右
6
新知探究
说一说
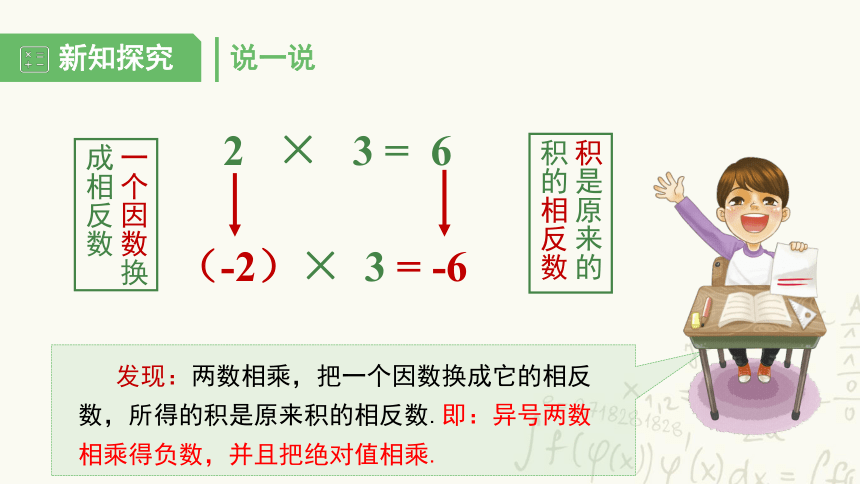
2 × 3 = 6
(-2)× 3 = -6
一个因数换成相反数
积是原来的积的相反数
发现:两数相乘,把一个因数换成它的相反数,所得的积是原来积的相反数.即:异号两数相乘得负数,并且把绝对值相乘.
新知探究
练一练
如图1-20,我们把向东走的路程记为正数.如果小丽从点O出发,以5km/h的速度向西行走3h后,请问小丽现在的位置是从点O向哪个方向行走了多少千米?
解析:
(- 5)×3 = -(5×3)=-15
答:小丽从O点向西走了15千米.
新知探究
符号的确定
2 x 1 = 2
2 x 0 = 0
(-2) x 1 =-2
(-2) x 0 = 0
2 x (-1)=-2
2 x (-2)=-4
(-2) x (-1)=2
(-2) x (-2)=4
新知探究
小归纳
一般规定:
异号两数相乘得负数,并且把绝对值相乘.
同号两数相乘得正数,并且把绝对值相乘.
(-)×(+)→(-)
任何数与0相乘,都得0.
新知探究
思考
讨论:
(1)若a<0,b>0,则ab____0 ;
(2)若a<0,b<0,则ab____0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号且a、b均不为0
a、b异号且a、b均不为0
新知探究
议一议
填空:
(1)(-2 )× 4 = -8 ,
4 × ( -2 ) = -8 ;
(2)[(-2 )×(-3 )]×( -4 )
= 6 ×( - 4 )= -24 ,
( -2 ) × [( - 3 )×( -4 )]
= ( -2 )× 12 = -24 .
从上面的填空题中,你发现了什么?
新知探究
乘法运算律学习
有理数的乘法的运算律:
乘法交换律:a×b =b×a
乘法结合律:(a×b)×c=a×(b×c)
乘法对加法的分配律(简称为分配律):
a ×( b + c ) = a × b + a × c .
新知探究
练一练
计算(-2)×( 3- ),用乘法分配律计算过程正确的是( )
B.(-2)×3-(-2)×(- )
C.2×3-(-2)×(- )
D.(-2)×3+2×(- )
A
A.(-2)×3+(-2)×(- )
03 典型例题
典型例题
1.计算:
(1) 3.5 ×(- 2)= -(3.5×2)=-7 ;
(2)(-3/8)×2/9 = -(3/8×2/9)= - 1/12 ;
(3)(-3)×(-1/3)=3×1/3=1;
(4)(-0.57)×0 = 0 .
(1) 3.5 ×(- 2); (2)(-3/8)×2/9 ;
(3)(-3)×(-1/3 ); (4)(-0.57)×0 ; .
解:
(1)( -8 )× 4 ×( -1 )×( -3 ) ;
(2) - (1/5 )× ( -10 )× ( -3.2 )×( -5 )
解析:
2.计算:
(1)(- 8)× 4×(-1)×(-3)= -(8×4×1×3)=-96 ;
(2) -(1/5 )×(-10)×(-3.2)×(-5)
= 1/5× 10 × 3.2× 5 = 32.
先确定积的符号,再把绝对值相乘.
典型例题
选择
3.若 ab>0,则必有 ( )
A. a>0,b>0 B. a<0,b<0
C. a>0,b<0 D. a>0,b>0或a<0,b<0
4.若 ab = 0,则一定有( )
a=b=0 B. a,b至少有一个为0
C. a=0 D. a,b最多有一个为0
D
B
典型例题
填空
被乘数 乘数 积的符号 积的绝对值 结果
-5 7
15 6
-30 -6
4 -25
-
35
-35
+
90
+
180
-
100
90
180
-100
5.填空
典型例题
(1)
(2)
(3)
(4)
解析:
6.计算
典型例题
04 拓展提高
拓展提高
应用
1.商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?
解:
(-5)×60=-300(元)
答:销售额减少300元.
拓展提高
应用
2.气象观测统计资料表明,在一般情况下,高度每上升1km,气温下降6℃.已知甲地现在地面气温为21℃,求甲地上空9km处的气温大约是多少.
解:(-6)×9=-54(℃);
21+(-54)=-33(℃).
答:甲地上空9km处的气温大约为-33℃.
05 课堂小结
课堂小结
有理数乘法
有理数乘法运算律
多个有理数相乘
乘法交换律:a×b=b×a
分配律:
a×(b+c)=a×b+a×c
几个不是零的数相乘,负因数的个数为奇数时,积为负数;偶数时,积为正数.
有一个因数为0,积为0.
乘法结合律:
(a×b)×c = a×(b×c)
06 作业布置
作业布置
1、练习:课本P32练习
2、预习新课
谢 谢 观 看
有理数的乘法
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
1、如果蜗牛从0处一直以每分钟2cm的速度向右爬行(规定:向右为正)那么3分钟后蜗牛在什么位置?
-2
0
2
4
6
8
2 + 2 + 2 = 6
新课导入
2.如果蜗牛一直以每分钟2cm的速度向左爬行(规定:向右为正)那么3分钟后蜗牛又将在0的什么位置?
-6
-4
-2
0
2
4
(-2)+(-2)+(-2)= -6
除了用加法,我们是否可以用乘法来表示位置的移动呢?
02 新知探究
新知探究
想一想
甲水库的水位每天升高3cm,乙水库的水位每天下降3cm,如果规定上升为正,下降为负,4天后,甲、乙水库水位的总变化量是多少?
我们是不是可以得出这样的算式:
3+3+3+3=3×4=12,
(-3)+(-3)+(-3)+(-3)=(-3)× 4 = -12
新知探究
想一想
(?3)×0 =_____.
0
(?3)×4=(?3)+(?3)+(?3)+(?3) =?12
(?3)×3 = _____________=_____,
(?3)×2 =_____________=_____,
(?3)×1 =_____,
?9
?6
类比前面得到的式子,能否将下面的空填好呢?
(?3)+(?3)+(?3)
(?3)+(?3)
3×4=3+3+3+3 = 12
?3
新知探究
乘法概念学习
如图,一只蜗牛沿直线L爬行,它现在的位置在L上的点O.
O
1.如果一只蜗牛向右爬行2cm记为+2cm,那么向左爬行2cm应该记为 .
2.如果3分钟以后记为+3分钟,那么3分钟以前应该记为__________.
-2cm
-3分钟
新知探究
规定:向左为负,向右为正.现在前为负,现在后为正.
结果:3分钟后在L上点O 边 cm处
表示: .
(+2)×(+3)= 6
(1)如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置?
O
2
6
4
l
乘法概念学习
右
6
新知探究
说一说
2 × 3 = 6
(-2)× 3 = -6
一个因数换成相反数
积是原来的积的相反数
发现:两数相乘,把一个因数换成它的相反数,所得的积是原来积的相反数.即:异号两数相乘得负数,并且把绝对值相乘.
新知探究
练一练
如图1-20,我们把向东走的路程记为正数.如果小丽从点O出发,以5km/h的速度向西行走3h后,请问小丽现在的位置是从点O向哪个方向行走了多少千米?
解析:
(- 5)×3 = -(5×3)=-15
答:小丽从O点向西走了15千米.
新知探究
符号的确定
2 x 1 = 2
2 x 0 = 0
(-2) x 1 =-2
(-2) x 0 = 0
2 x (-1)=-2
2 x (-2)=-4
(-2) x (-1)=2
(-2) x (-2)=4
新知探究
小归纳
一般规定:
异号两数相乘得负数,并且把绝对值相乘.
同号两数相乘得正数,并且把绝对值相乘.
(-)×(+)→(-)
任何数与0相乘,都得0.
新知探究
思考
讨论:
(1)若a<0,b>0,则ab____0 ;
(2)若a<0,b<0,则ab____0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号且a、b均不为0
a、b异号且a、b均不为0
新知探究
议一议
填空:
(1)(-2 )× 4 = -8 ,
4 × ( -2 ) = -8 ;
(2)[(-2 )×(-3 )]×( -4 )
= 6 ×( - 4 )= -24 ,
( -2 ) × [( - 3 )×( -4 )]
= ( -2 )× 12 = -24 .
从上面的填空题中,你发现了什么?
新知探究
乘法运算律学习
有理数的乘法的运算律:
乘法交换律:a×b =b×a
乘法结合律:(a×b)×c=a×(b×c)
乘法对加法的分配律(简称为分配律):
a ×( b + c ) = a × b + a × c .
新知探究
练一练
计算(-2)×( 3- ),用乘法分配律计算过程正确的是( )
B.(-2)×3-(-2)×(- )
C.2×3-(-2)×(- )
D.(-2)×3+2×(- )
A
A.(-2)×3+(-2)×(- )
03 典型例题
典型例题
1.计算:
(1) 3.5 ×(- 2)= -(3.5×2)=-7 ;
(2)(-3/8)×2/9 = -(3/8×2/9)= - 1/12 ;
(3)(-3)×(-1/3)=3×1/3=1;
(4)(-0.57)×0 = 0 .
(1) 3.5 ×(- 2); (2)(-3/8)×2/9 ;
(3)(-3)×(-1/3 ); (4)(-0.57)×0 ; .
解:
(1)( -8 )× 4 ×( -1 )×( -3 ) ;
(2) - (1/5 )× ( -10 )× ( -3.2 )×( -5 )
解析:
2.计算:
(1)(- 8)× 4×(-1)×(-3)= -(8×4×1×3)=-96 ;
(2) -(1/5 )×(-10)×(-3.2)×(-5)
= 1/5× 10 × 3.2× 5 = 32.
先确定积的符号,再把绝对值相乘.
典型例题
选择
3.若 ab>0,则必有 ( )
A. a>0,b>0 B. a<0,b<0
C. a>0,b<0 D. a>0,b>0或a<0,b<0
4.若 ab = 0,则一定有( )
a=b=0 B. a,b至少有一个为0
C. a=0 D. a,b最多有一个为0
D
B
典型例题
填空
被乘数 乘数 积的符号 积的绝对值 结果
-5 7
15 6
-30 -6
4 -25
-
35
-35
+
90
+
180
-
100
90
180
-100
5.填空
典型例题
(1)
(2)
(3)
(4)
解析:
6.计算
典型例题
04 拓展提高
拓展提高
应用
1.商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?
解:
(-5)×60=-300(元)
答:销售额减少300元.
拓展提高
应用
2.气象观测统计资料表明,在一般情况下,高度每上升1km,气温下降6℃.已知甲地现在地面气温为21℃,求甲地上空9km处的气温大约是多少.
解:(-6)×9=-54(℃);
21+(-54)=-33(℃).
答:甲地上空9km处的气温大约为-33℃.
05 课堂小结
课堂小结
有理数乘法
有理数乘法运算律
多个有理数相乘
乘法交换律:a×b=b×a
分配律:
a×(b+c)=a×b+a×c
几个不是零的数相乘,负因数的个数为奇数时,积为负数;偶数时,积为正数.
有一个因数为0,积为0.
乘法结合律:
(a×b)×c = a×(b×c)
06 作业布置
作业布置
1、练习:课本P32练习
2、预习新课
谢 谢 观 看
同课章节目录
