湘教版七年级数学上册第1章 有理数1.5.2 有理数的除法教学课件(共33张)
文档属性
| 名称 | 湘教版七年级数学上册第1章 有理数1.5.2 有理数的除法教学课件(共33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 00:00:00 | ||
图片预览










文档简介
(共33张PPT)
有理数的除法
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
同学们能很快地说出下列算式的结果吗?
小学时我们就知道除法是乘法的逆运算,那它在有理数的运算中也满足吗?
乘法 除法
2×3=6
3×4=12
0×3=0
3
2
4
3
0
02 新知探究
新知探究
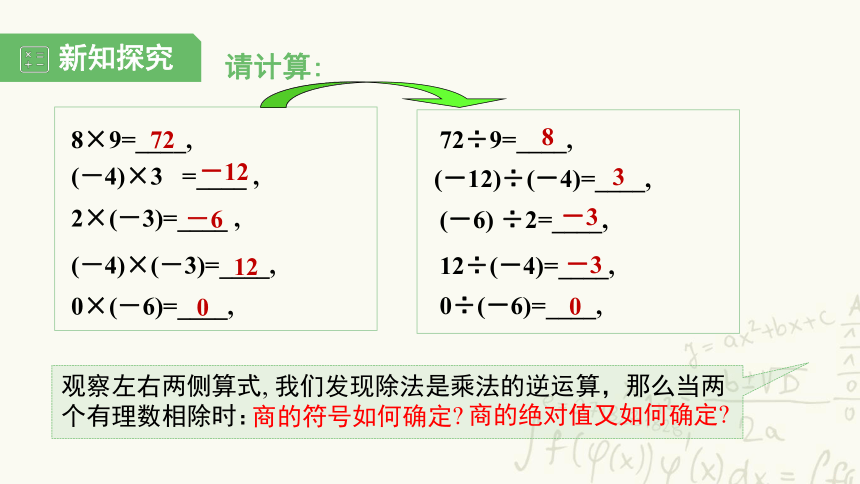
2×(-3)=____ ,
(-4)×(-3)=____,
8×9=____,
0×(-6)=____,
(-4)×3 =____ ,
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-12)÷(-4)=____,
0÷(-6)=____,
观察左右两侧算式, 我们发现除法是乘法的逆运算,那么当两个有理数相除时:
商的符号如何确定?
商的绝对值又如何确定?
-6
72
-12
0
-3
-3
0
3
请计算:
12
8
新知探究
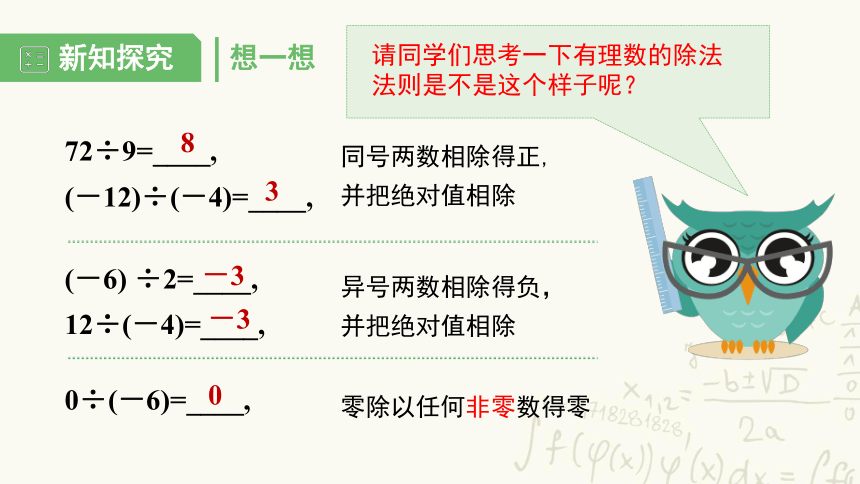
想一想
(-6) ÷2=____,
12÷(-4)=____,
0÷(-6)=____,
-3
-3
0
异号两数相除得负,
并把绝对值相除
零除以任何非零数得零
72÷9=____,
(-12)÷(-4)=____,
8
同号两数相除得正,
并把绝对值相除
3
请同学们思考一下有理数的除法法则是不是这个样子呢?
新课导入
观察
我们知道 2 × 3 = 6,
因此 6 ÷ 3 = 2.
那么又该如何计算以下算式呢?
( - 6 ) ÷ 3 ,
6 ÷ ( -3 ) ,
( -6 ) ÷ ( -3 )
新知探究
除法概念
(- 6)÷3 = ? 6 ÷(-3)= ? (- 6)÷(- 3)= ?
由于( - 2 )× 3 = - 6 ,
因此( - 6 )÷3 = - 2 .
类似 由于 ( - 2 ) × ( - 3 ) = 6 ,
因此 6 ÷ ( - 3 ) = - 2
新知探究
除法概念
有理数的除法运算:对于两个有理数 a,b,其中b≠0,如果有一个有理数c,使得c b =a ,
那么规定 a÷b =c, 且把 c 叫做 a 除以 b 的商.
新知探究
除法法则
知道了有理数除法的概念,又根据前面的观察,我们是否可以得出有理数除法的运算法则呢?
新知探究
除法法则
同号两数相除得正数,异号两数相除得负数,并把它们的绝对值相除;
0除以任何一个不等于0的数都得0.
即: (+)÷(+)→(+)
(-)÷(-)→(+)
(-)÷(+)→(-)
(+)÷(-)→(-)
新知探究
练一练
(1)(-15)÷(-3)
(2)12 ÷(- )
解:原式=-(12÷ )=-48
1
4
(3)(-0.75)÷0.25
解:原式=-(0.75 ÷ 0.25)=-3
解:原式= +(15÷3)=5
1
4
新知探究
练一练
计算:
(1) ×2; (2)(- )×(-2).
解:(1) ×2 = 1
(2)( )×(-2)= 1
观察上面两题有何特点?
有理数中仍然这个结论仍然成立:乘积是1的两个数互为倒数.
新知探究
倒数概念
定义:一般地,如果两个数的乘积等于1,我们把其中一个数叫做另一个数的倒数,也称它们互为倒数.
注意:1.正数的倒数是正数,负数的倒数是负数;
2.分数的倒数是分子与分母颠倒位置;
3.求小数的倒数,先化成分数,再求倒数;
4.0没有倒数.
新知探究
想一想
根据前面提到的倒数的概念,是不是可以很简单地想到除以一个不为零的数便可以转换成乘他的倒数呢?
我们已经知道 10 ÷( - 5 )= - 2 ,
又 10 ×(- 1/5)= - 2 ,
所以 10 ÷( - 5 )= 10 ×(- 1 /5 )
试问 10÷(-5)还可以怎样计算?
新知探究
小归纳
一般地,有理数的除法运算可以转化为乘法运算,即除以一个不等于零的数等于乘这个数的倒数.也可以表示成
a÷b =a×(1/b)(b≠0)
新知探究
练一练
(-12)÷ 1/3 ; (2) 15÷ (-3/7 );
解析:
(1) (-12)÷ 1/3 =(-12)× 3= -36;
(2) 15÷ (-3 / 7 )= 15× (- 7/ 3 )= -35
03 典型例题
例题讲解
1.计算:
(1)(-24)÷ 4 ; (2)(-18)÷(- 9);
(3) 10÷(-5) .
解析:
(1)(-24)÷4 = -(24÷4)= - 6 ;
(2)(-18)÷(-9)= +(18÷9)= 2 ;
(3) 10÷( -5 )= -(10÷5)= - 2 .
例题讲解
2.计算
(1)(-24)÷(-6); (2)-3.5÷6×(-3/4);
(3)(-6)÷(-4)×(2/7).
解析:
(1)(-24)÷(-6)=-24×(-1/6)= 4
(2) -3.5÷6×(-3/4)=-3.5×1/6 ×(-3/4)= 7/16
(3)(-6)÷(-4)×(2/7)=(-6)×(-1/4)×(2/7)= 3/7
例题讲解
3.计算
(1) ( -56 ) ÷ ( -2 ) ÷ ( -8 ) ;
(2) ( -10)÷[ ( -5 ) × ( -2 ) ] ;
解析:
(1)( -56 )÷(-2)÷(-8)= 28÷(-8)= -7/2 ;
(2)( -10)÷[(-5)×(-2) ]=(-10)÷10 = -1 ;
(1)若a、b互为相反数,且 ab, =________,
2a + 2b =________;
(3)若 a > b, < 0,则 a、b 的符号分别是________________.
(2)当 时, =_______;
a >0,b < 0
4.填空
例题讲解
(1)1的倒数为_____;
(2)-1的倒数为______;
(3) 的倒数为______;
(4) 的倒数为______;
(5) 的倒数为_____;
(6) 的倒数为______.
1
-1
3
-3
不对,只有当a≠0时,a的倒数是 .
思考:a的倒数是 吗?
5.填空
例题讲解
解:
6.计算
例题讲解
04 拓展提高
拓展提高
应用
1.a,b,c为非零有理数,求 的值.
解:分a,b,c中只有1个负数、2个负数、3个负数、全部都是正数四种情况分别讨论
当a<0,b>0,c>0时,
原式= = -1+1+(-1)+(-1)=-2;
当a<0,b<0,c>0时,
原式= = 1+(-1)+(-1)+1=0;
拓展提高
应用
解:当a<0,b<0,c<0时,
原式= = 1+1+1+(-1)=2
当a>0,b>0,c>0时,
原式= =4.
05 课堂小结
课堂小结
有理数除法法则
0除以任何非0的数都得0.
两个有理数相除,同号得正,异号得负,并把绝对值相除.
除以一个数等于乘这个数的倒数.
06 作业布置
作业布置
(1)24÷(-3)÷(-4) ; (2)(-6)÷(-2)÷3;
(3)2÷(-7)×(-4); (4)18÷6×(-2).
(1)24÷(-3)÷(-4)= -8 ÷(-4)= 2 ;
(2)(-6)÷(-2)÷3 = 3÷3 = 1 ;
(3)2÷(-7)×(-4) = ( ) ×(-4) = ;
解析:
(4)18÷6×(-2) = 3×(-2)= -6.
谢 谢 观 看
有理数的除法
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
同学们能很快地说出下列算式的结果吗?
小学时我们就知道除法是乘法的逆运算,那它在有理数的运算中也满足吗?
乘法 除法
2×3=6
3×4=12
0×3=0
3
2
4
3
0
02 新知探究
新知探究
2×(-3)=____ ,
(-4)×(-3)=____,
8×9=____,
0×(-6)=____,
(-4)×3 =____ ,
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-12)÷(-4)=____,
0÷(-6)=____,
观察左右两侧算式, 我们发现除法是乘法的逆运算,那么当两个有理数相除时:
商的符号如何确定?
商的绝对值又如何确定?
-6
72
-12
0
-3
-3
0
3
请计算:
12
8
新知探究
想一想
(-6) ÷2=____,
12÷(-4)=____,
0÷(-6)=____,
-3
-3
0
异号两数相除得负,
并把绝对值相除
零除以任何非零数得零
72÷9=____,
(-12)÷(-4)=____,
8
同号两数相除得正,
并把绝对值相除
3
请同学们思考一下有理数的除法法则是不是这个样子呢?
新课导入
观察
我们知道 2 × 3 = 6,
因此 6 ÷ 3 = 2.
那么又该如何计算以下算式呢?
( - 6 ) ÷ 3 ,
6 ÷ ( -3 ) ,
( -6 ) ÷ ( -3 )
新知探究
除法概念
(- 6)÷3 = ? 6 ÷(-3)= ? (- 6)÷(- 3)= ?
由于( - 2 )× 3 = - 6 ,
因此( - 6 )÷3 = - 2 .
类似 由于 ( - 2 ) × ( - 3 ) = 6 ,
因此 6 ÷ ( - 3 ) = - 2
新知探究
除法概念
有理数的除法运算:对于两个有理数 a,b,其中b≠0,如果有一个有理数c,使得c b =a ,
那么规定 a÷b =c, 且把 c 叫做 a 除以 b 的商.
新知探究
除法法则
知道了有理数除法的概念,又根据前面的观察,我们是否可以得出有理数除法的运算法则呢?
新知探究
除法法则
同号两数相除得正数,异号两数相除得负数,并把它们的绝对值相除;
0除以任何一个不等于0的数都得0.
即: (+)÷(+)→(+)
(-)÷(-)→(+)
(-)÷(+)→(-)
(+)÷(-)→(-)
新知探究
练一练
(1)(-15)÷(-3)
(2)12 ÷(- )
解:原式=-(12÷ )=-48
1
4
(3)(-0.75)÷0.25
解:原式=-(0.75 ÷ 0.25)=-3
解:原式= +(15÷3)=5
1
4
新知探究
练一练
计算:
(1) ×2; (2)(- )×(-2).
解:(1) ×2 = 1
(2)( )×(-2)= 1
观察上面两题有何特点?
有理数中仍然这个结论仍然成立:乘积是1的两个数互为倒数.
新知探究
倒数概念
定义:一般地,如果两个数的乘积等于1,我们把其中一个数叫做另一个数的倒数,也称它们互为倒数.
注意:1.正数的倒数是正数,负数的倒数是负数;
2.分数的倒数是分子与分母颠倒位置;
3.求小数的倒数,先化成分数,再求倒数;
4.0没有倒数.
新知探究
想一想
根据前面提到的倒数的概念,是不是可以很简单地想到除以一个不为零的数便可以转换成乘他的倒数呢?
我们已经知道 10 ÷( - 5 )= - 2 ,
又 10 ×(- 1/5)= - 2 ,
所以 10 ÷( - 5 )= 10 ×(- 1 /5 )
试问 10÷(-5)还可以怎样计算?
新知探究
小归纳
一般地,有理数的除法运算可以转化为乘法运算,即除以一个不等于零的数等于乘这个数的倒数.也可以表示成
a÷b =a×(1/b)(b≠0)
新知探究
练一练
(-12)÷ 1/3 ; (2) 15÷ (-3/7 );
解析:
(1) (-12)÷ 1/3 =(-12)× 3= -36;
(2) 15÷ (-3 / 7 )= 15× (- 7/ 3 )= -35
03 典型例题
例题讲解
1.计算:
(1)(-24)÷ 4 ; (2)(-18)÷(- 9);
(3) 10÷(-5) .
解析:
(1)(-24)÷4 = -(24÷4)= - 6 ;
(2)(-18)÷(-9)= +(18÷9)= 2 ;
(3) 10÷( -5 )= -(10÷5)= - 2 .
例题讲解
2.计算
(1)(-24)÷(-6); (2)-3.5÷6×(-3/4);
(3)(-6)÷(-4)×(2/7).
解析:
(1)(-24)÷(-6)=-24×(-1/6)= 4
(2) -3.5÷6×(-3/4)=-3.5×1/6 ×(-3/4)= 7/16
(3)(-6)÷(-4)×(2/7)=(-6)×(-1/4)×(2/7)= 3/7
例题讲解
3.计算
(1) ( -56 ) ÷ ( -2 ) ÷ ( -8 ) ;
(2) ( -10)÷[ ( -5 ) × ( -2 ) ] ;
解析:
(1)( -56 )÷(-2)÷(-8)= 28÷(-8)= -7/2 ;
(2)( -10)÷[(-5)×(-2) ]=(-10)÷10 = -1 ;
(1)若a、b互为相反数,且 ab, =________,
2a + 2b =________;
(3)若 a > b, < 0,则 a、b 的符号分别是________________.
(2)当 时, =_______;
a >0,b < 0
4.填空
例题讲解
(1)1的倒数为_____;
(2)-1的倒数为______;
(3) 的倒数为______;
(4) 的倒数为______;
(5) 的倒数为_____;
(6) 的倒数为______.
1
-1
3
-3
不对,只有当a≠0时,a的倒数是 .
思考:a的倒数是 吗?
5.填空
例题讲解
解:
6.计算
例题讲解
04 拓展提高
拓展提高
应用
1.a,b,c为非零有理数,求 的值.
解:分a,b,c中只有1个负数、2个负数、3个负数、全部都是正数四种情况分别讨论
当a<0,b>0,c>0时,
原式= = -1+1+(-1)+(-1)=-2;
当a<0,b<0,c>0时,
原式= = 1+(-1)+(-1)+1=0;
拓展提高
应用
解:当a<0,b<0,c<0时,
原式= = 1+1+1+(-1)=2
当a>0,b>0,c>0时,
原式= =4.
05 课堂小结
课堂小结
有理数除法法则
0除以任何非0的数都得0.
两个有理数相除,同号得正,异号得负,并把绝对值相除.
除以一个数等于乘这个数的倒数.
06 作业布置
作业布置
(1)24÷(-3)÷(-4) ; (2)(-6)÷(-2)÷3;
(3)2÷(-7)×(-4); (4)18÷6×(-2).
(1)24÷(-3)÷(-4)= -8 ÷(-4)= 2 ;
(2)(-6)÷(-2)÷3 = 3÷3 = 1 ;
(3)2÷(-7)×(-4) = ( ) ×(-4) = ;
解析:
(4)18÷6×(-2) = 3×(-2)= -6.
谢 谢 观 看
同课章节目录
