湘教版七年级数学上册第1章 有理数1.2.3 绝对值教学课件(共31张)
文档属性
| 名称 | 湘教版七年级数学上册第1章 有理数1.2.3 绝对值教学课件(共31张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 09:41:28 | ||
图片预览








文档简介
(共31张PPT)
绝对值
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
观察
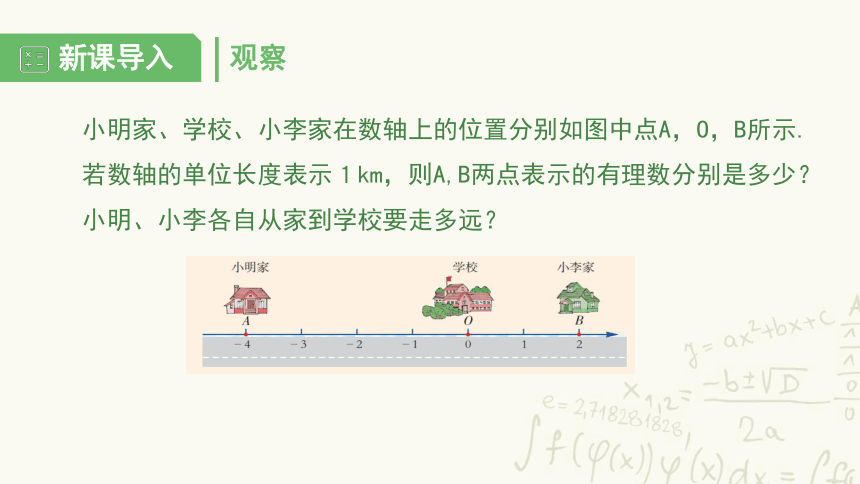
小明家、学校、小李家在数轴上的位置分别如图中点A,O,B所示.若数轴的单位长度表示1km,则A,B两点表示的有理数分别是多少?小明、小李各自从家到学校要走多远?
新课导入
观察
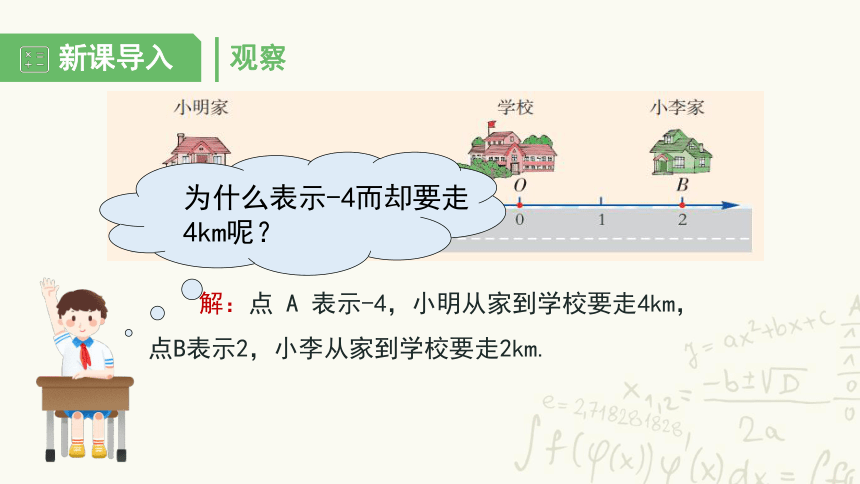
解:点 A 表示-4,小明从家到学校要走4km,点B表示2,小李从家到学校要走2km.
为什么表示-4而却要走4km呢?
02 新知探究
新知探究
绝对值的概念
两辆汽车从同一处O 出发,分别向东、西方向行驶10km,到达A、B 两处(如图所示).它们的行驶路线相同吗?它们行驶路程的远近(线段OA、OB的长度)相同吗?
解:由图可知行驶的路线不相同,方向刚好相反,行驶的路程远近相同,都为10km.
A
O
B
新知探究
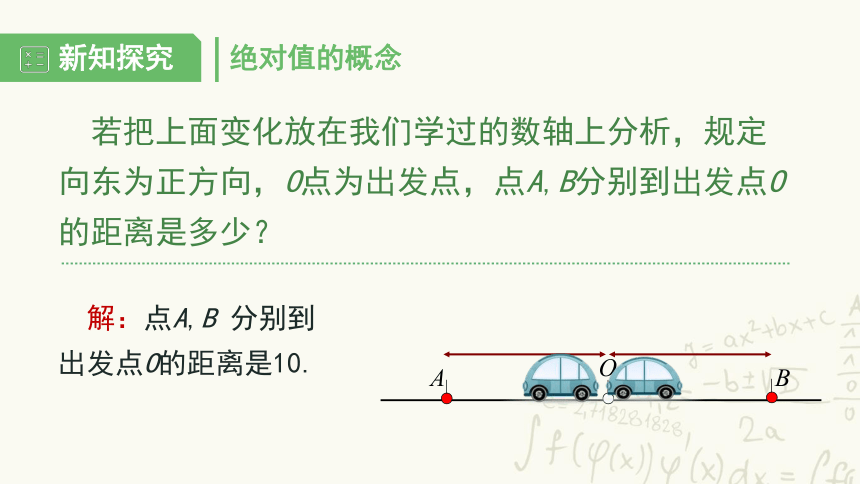
若把上面变化放在我们学过的数轴上分析,规定向东为正方向,O点为出发点,点A,B分别到出发点O的距离是多少?
解:点A,B 分别到出发点O的距离是10.
绝对值的概念
A
O
B
新知探究
绝对值的概念
在数轴上,一个数所对应的点与原点的距离叫做该数的
绝对值。绝对值的符号:| |。
例如:-1.5的绝对值为1.5,记作|-1.5|=1.5
一般地,数学上规定:
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
新知探究
练一练
求下列各数的绝对值:
解:
新知探究
绝对值的意义
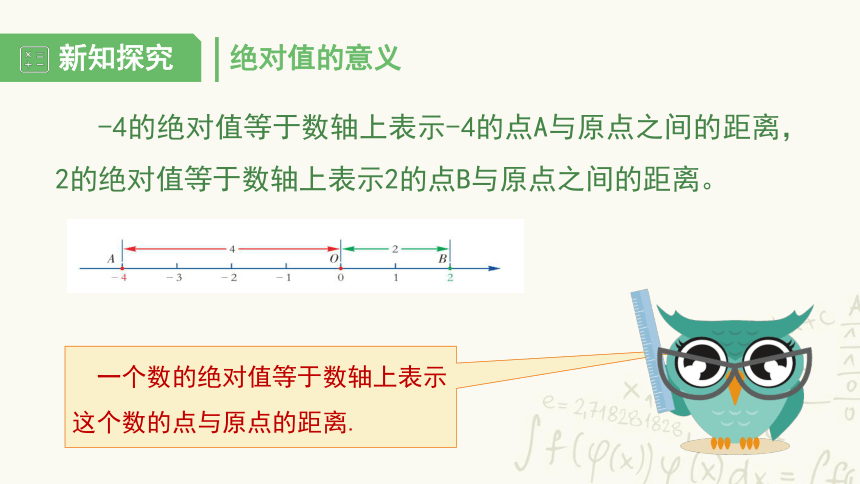
-4的绝对值等于数轴上表示-4的点A与原点之间的距离,2的绝对值等于数轴上表示2的点B与原点之间的距离。
一个数的绝对值等于数轴上表示这个数的点与原点的距离.
新知探究
如果a表示有理数,那么│a│有什么含义?
解:∣a∣表示数a的绝对值;
∣a∣表示数轴上数a对应的点与原点的距离.
新知探究
一个数的绝对值是它本身,这个数是( ).
正数或零
一个数的绝对值是它的相反数,这个数是( ).
负数或零
绝对值的意义
新知探究
如果 | a | = a , 则 a ? 0 .
绝对值的意义
新知探究
a (a>0)
0 (a=0)
-a (a<0)
︱a︱=
或者:
绝对值的意义
即:
新知探究
议一议
1.怎样表示a的相反数?
a
-a
相反数
新知探究
议一议
2. 若|a|= |b|,则a与b有什么关系?
a=b
a=-b
03 典型例题
例题讲解
答案解析:
1.求下列各数的绝对值.
12,-7.5, 0.
|12|=12;
|-7.5|=7.5;
|0|=0
(正数的绝对值等于它本身)
(负数的绝对值等于它的相反数)
(0的绝对值是0)
例题讲解
解:|+4|=4 |-4|=4
2.求绝对值等于4的数。
绝对值等于4的数是+4和-4.
(1)一个数的绝对值是2?,则这数是2。
(2)|5|=|-5|。
(3)|-0.3|=|0.3|。
(4)|3|>0。
(5)|-1.4|>0。
3.判断
例题讲解
4.任何一个有理数的绝对值一定( )
D
A.大于0 B.小于0
C.小于或等于0 D.大于或等于0
例题讲解
(1)|2|=______,|-2|=______.
(2)若|x|=4,则x=_____.
(3)若|a|=0,则a=______.
(4)|-6|的相反数是______.
(5)+7.2的相反数的绝对值是______.
±4
2
-6
7.2
2
0
5.填空
例题讲解
04 拓展提高
应用
1.第55届世乒赛于2019年4月21日至4月28日在匈牙利举办,此次比赛中用球的质量有严格的规定,下表是6个乒乓球质量检测的结果(单位:克,超过标准质量的克数记为正数).
一号球 二号球 三号球 四号球 五号球 六号球
-0.5 0.1 0.2 0 -0.08 -0.15
若规定与标准质量误差不超过0.1g的为优等品,超过0.1g但不超过0.3g的为合格品,在这六个乒乓球中,优等品、合格品和不合格品分别是哪几个乒乓球?请说明理由.
解:一号球|-0.5|=0.5,不合格,二号球|0.1|=0.1,优等品,三号球|0.2|=0.2,合格品,四号球|0|=0,优等品,五号球|-0.08|=0.08,优等品,六号球
|-0.15|=0.15,合格品.
拓展提高
拓展提高
应用
解析:由绝对值的性质可得|a-3|≥0,|b-2015|≥0.
2.若|a-3|+|b-2015|=0,求a,b的值.
解:由题意得|a-3|≥0,|b-2015|≥0,又因为|a-3|+|b-2015|=0,所以|a-3|=0,|b-2015|=0,所以a=3,b=2015.
05 课堂小结
课堂小结
绝对值
定义
应用
几何意义
代数意义
求一个数的绝对值
由绝对值求数
在数轴上,表示数a到原点的距离.
用绝对值解决实际问题
︱a︱=
a (a>0)
0 (a=0)
-a (a<0)
06 作业布置
作业布置
课本P12第2题
谢 谢 观 看
绝对值
教学课件
湘教版七年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
观察
小明家、学校、小李家在数轴上的位置分别如图中点A,O,B所示.若数轴的单位长度表示1km,则A,B两点表示的有理数分别是多少?小明、小李各自从家到学校要走多远?
新课导入
观察
解:点 A 表示-4,小明从家到学校要走4km,点B表示2,小李从家到学校要走2km.
为什么表示-4而却要走4km呢?
02 新知探究
新知探究
绝对值的概念
两辆汽车从同一处O 出发,分别向东、西方向行驶10km,到达A、B 两处(如图所示).它们的行驶路线相同吗?它们行驶路程的远近(线段OA、OB的长度)相同吗?
解:由图可知行驶的路线不相同,方向刚好相反,行驶的路程远近相同,都为10km.
A
O
B
新知探究
若把上面变化放在我们学过的数轴上分析,规定向东为正方向,O点为出发点,点A,B分别到出发点O的距离是多少?
解:点A,B 分别到出发点O的距离是10.
绝对值的概念
A
O
B
新知探究
绝对值的概念
在数轴上,一个数所对应的点与原点的距离叫做该数的
绝对值。绝对值的符号:| |。
例如:-1.5的绝对值为1.5,记作|-1.5|=1.5
一般地,数学上规定:
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
新知探究
练一练
求下列各数的绝对值:
解:
新知探究
绝对值的意义
-4的绝对值等于数轴上表示-4的点A与原点之间的距离,2的绝对值等于数轴上表示2的点B与原点之间的距离。
一个数的绝对值等于数轴上表示这个数的点与原点的距离.
新知探究
如果a表示有理数,那么│a│有什么含义?
解:∣a∣表示数a的绝对值;
∣a∣表示数轴上数a对应的点与原点的距离.
新知探究
一个数的绝对值是它本身,这个数是( ).
正数或零
一个数的绝对值是它的相反数,这个数是( ).
负数或零
绝对值的意义
新知探究
如果 | a | = a , 则 a ? 0 .
绝对值的意义
新知探究
a (a>0)
0 (a=0)
-a (a<0)
︱a︱=
或者:
绝对值的意义
即:
新知探究
议一议
1.怎样表示a的相反数?
a
-a
相反数
新知探究
议一议
2. 若|a|= |b|,则a与b有什么关系?
a=b
a=-b
03 典型例题
例题讲解
答案解析:
1.求下列各数的绝对值.
12,-7.5, 0.
|12|=12;
|-7.5|=7.5;
|0|=0
(正数的绝对值等于它本身)
(负数的绝对值等于它的相反数)
(0的绝对值是0)
例题讲解
解:|+4|=4 |-4|=4
2.求绝对值等于4的数。
绝对值等于4的数是+4和-4.
(1)一个数的绝对值是2?,则这数是2。
(2)|5|=|-5|。
(3)|-0.3|=|0.3|。
(4)|3|>0。
(5)|-1.4|>0。
3.判断
例题讲解
4.任何一个有理数的绝对值一定( )
D
A.大于0 B.小于0
C.小于或等于0 D.大于或等于0
例题讲解
(1)|2|=______,|-2|=______.
(2)若|x|=4,则x=_____.
(3)若|a|=0,则a=______.
(4)|-6|的相反数是______.
(5)+7.2的相反数的绝对值是______.
±4
2
-6
7.2
2
0
5.填空
例题讲解
04 拓展提高
应用
1.第55届世乒赛于2019年4月21日至4月28日在匈牙利举办,此次比赛中用球的质量有严格的规定,下表是6个乒乓球质量检测的结果(单位:克,超过标准质量的克数记为正数).
一号球 二号球 三号球 四号球 五号球 六号球
-0.5 0.1 0.2 0 -0.08 -0.15
若规定与标准质量误差不超过0.1g的为优等品,超过0.1g但不超过0.3g的为合格品,在这六个乒乓球中,优等品、合格品和不合格品分别是哪几个乒乓球?请说明理由.
解:一号球|-0.5|=0.5,不合格,二号球|0.1|=0.1,优等品,三号球|0.2|=0.2,合格品,四号球|0|=0,优等品,五号球|-0.08|=0.08,优等品,六号球
|-0.15|=0.15,合格品.
拓展提高
拓展提高
应用
解析:由绝对值的性质可得|a-3|≥0,|b-2015|≥0.
2.若|a-3|+|b-2015|=0,求a,b的值.
解:由题意得|a-3|≥0,|b-2015|≥0,又因为|a-3|+|b-2015|=0,所以|a-3|=0,|b-2015|=0,所以a=3,b=2015.
05 课堂小结
课堂小结
绝对值
定义
应用
几何意义
代数意义
求一个数的绝对值
由绝对值求数
在数轴上,表示数a到原点的距离.
用绝对值解决实际问题
︱a︱=
a (a>0)
0 (a=0)
-a (a<0)
06 作业布置
作业布置
课本P12第2题
谢 谢 观 看
同课章节目录
