14.1.1 直角三角形三边的关系 同步练习(解析版)
文档属性
| 名称 | 14.1.1 直角三角形三边的关系 同步练习(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 14:44:01 | ||
图片预览



文档简介
初中数学华师大版八年级上学期 第14章 14.1.1 直角三角形三边的关系
一、单选题
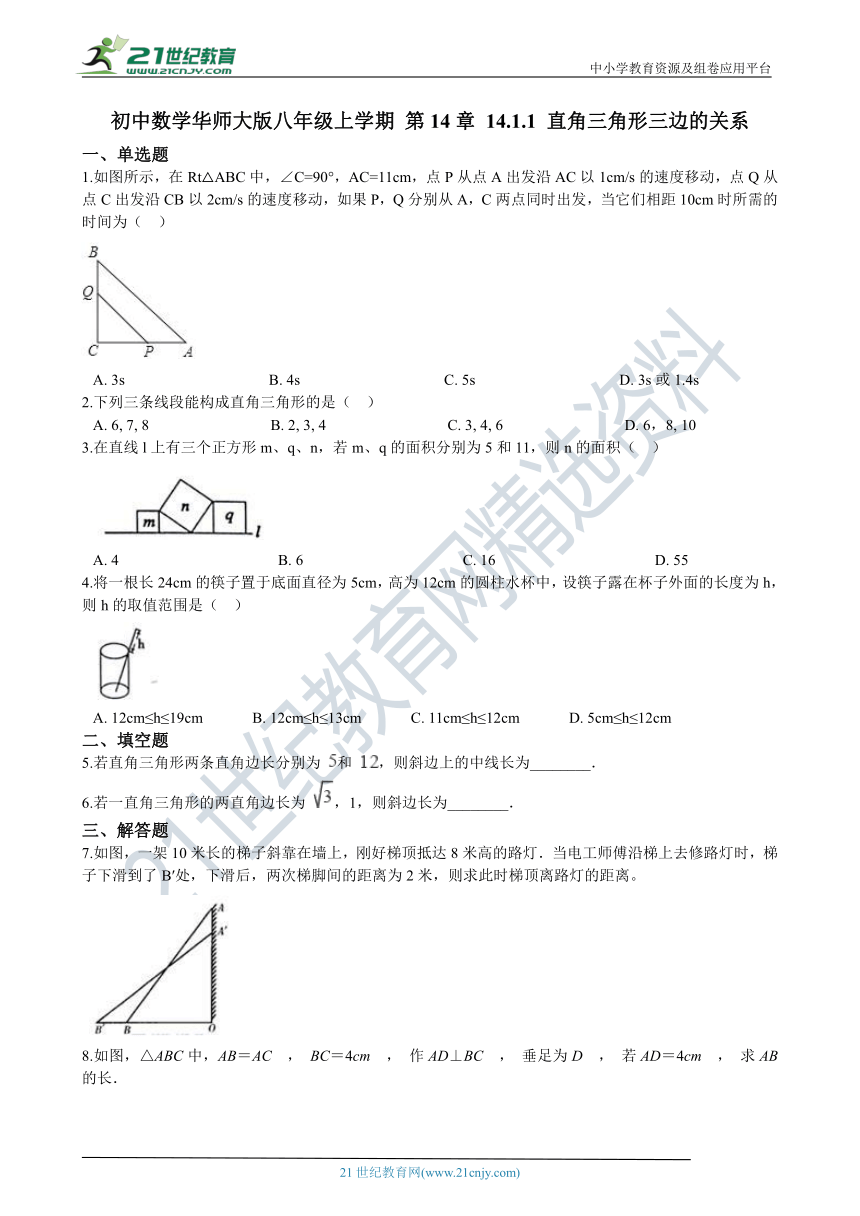
1.如图所示,在Rt△ABC中,∠C=90°,AC=11cm,点P从点A出发沿AC以1cm/s的速度移动,点Q从点C出发沿CB以2cm/s的速度移动,如果P,Q分别从A,C两点同时出发,当它们相距10cm时所需的时间为(?? ) 21世纪教育网版权所有
A.?3s??????????????????????????????????????B.?4s??????????????????????????????????????C.?5s??????????????????????????????????????D.?3s或1.4s
2.下列三条线段能构成直角三角形的是( ??)
A.?6, 7, 8????????????????????????????????B.?2, 3, 4????????????????????????????????C.?3, 4, 6????????????????????????????????D.?6,8, 10
3.在直线l上有三个正方形m、q、n,若m、q的面积分别为5和11,则n的面积( ??)
A.?4??????????????????????????????????????????B.?6??????????????????????????????????????????C.?16??????????????????????????????????????????D.?55
4.将一根长24cm的筷子置于底面直径为5cm,高为12cm的圆柱水杯中,设筷子露在杯子外面的长度为h,则h的取值范围是( ??) 21教育网
A.?12cm≤h≤19cm?????????????B.?12cm≤h≤13cm?????????????C.?11cm≤h≤12cm?????????????D.?5cm≤h≤12cm
二、填空题
5.若直角三角形两条直角边长分别为 和 ,则斜边上的中线长为________.
6.若一直角三角形的两直角边长为 ,1,则斜边长为________.
三、解答题
7.如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则求此时梯顶离路灯的距离。
8.如图,△ABC中,AB=AC , BC=4cm , 作AD⊥BC , 垂足为D , 若AD=4cm , 求AB的长. 21cnjy.com
9.如图,在Rt△ABC中,∠C=90°,AC=5,AB=13,求BC.
四、综合题
10.我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.21·cn·jy·com
(1)请你根据上述的规律写出下一组勾股数:
(2)若第一个数用字母n(n为奇数,且n≥3)表示,那么后两个数用含n的代数式分别表示为________和________,请用所学知识说明它们是一组勾股数. 2·1·c·n·j·y
11.如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5.
求:
(1)△ABC的周长;
(2)判断△ABC是否是直角三角形?为什么?
答案解析部分
一、单选题
1. D
解:设运动时间为ts时PQ=10cm,则CP=(11﹣x)cm,CQ=2xcm,
根据题意得:4x2+(11﹣x)2=100,
解得:x1=1.4,x2=3.
故答案为:D.
【分析】设运动时间为ts时PQ=10cm,根据路程等于速度乘以时间得出AP=tcm,CQ=2tcm,故CP=(11﹣x)cm,根据勾股定理建立方程,求解即可。21·世纪*教育网
2. D
解:A、最大边82=64<62+72=85, 为锐角三角形,A不符合题意; B、最大边42=16>32+22=13, 为钝角三角形,B不符合题意; C、最大边62=36>32+42=25, 为钝角三角形,C不符合题意; C、最大边102=100=62+82=100, 为直角三角形,D不符合题意; 故答案为:D 【分析】先找出最大边,然后根据勾股定理分析判断,最大边的平方小于另外两边的平方和是锐角三角形,等于另外两边的平方和是直角三角形,大于另外两边的平方和是钝角三角形。2-1-c-n-j-y
3. C
∵∠ACB+∠ECD=∠ACB+∠BAC=90°, ∴∠ABC=∠DEC,∠ACB=∠CDE,AC=CD, ∴△ACB≌△△DCE(AAS), ∴AB=CE,BC=DE, 由勾股定理可得,AC2=AB2+BC2=AB2+DE2 Sn=Sm+Sq=11+5=16. n的面积为16 21*cnjy*com
故答案为:C.
【分析】利用全等三角形判定定理证明,再利用勾股定理求得线段的关系,得到面积。
4. C
h最大时为筷子与杯底垂直时,h=12cm 最小时为筷子与杯底和杯高形成直角三角形时,AB= h=24-13=11cm, ∴11cm≤h≤12cm. 【来源:21cnj*y.co*m】
故答案为:C.
【分析】根据题意,找到h最小、最大值的情况,利用勾股定理解答。
二、填空题
5.
解:根据勾股定理,可求得斜边长为 ,所以斜边上的中线长为 .
故答案为: .
【分析】结合题意,由勾股定理即可计算得到斜边的长度,继而计算得到斜边上的中线长即可。
6. 2
解:斜边长= =2,
故答案为:2.
【分析】直接利用勾股定理计算即可.
三、解答题
7. 解:由题意得:BO= B'O=BO+BB'=6+2=8, ∴A'O= ∴AA‘=AO-A'O=8-6=2(米); 故答案为:2米. www-2-1-cnjy-com
【分析】由勾股定理求出BO的长,于是B'D的长可求,在△A'BO中,用勾股定理求出A'D的长,则此时梯顶离路灯的距离可求.【出处:21教育名师】
8. 解:∵AB=AC , BC=4cm , AD⊥BC ,
∴BD= BC=2,
∵AD=4cm ,
∴AB= =2 cm.
【分析】根据等腰三角形三线合一的性质可得BD的长,利用勾股定理求出AB的长即可.
9. 解:∵在Rt△ABC中,∠C=90°,AC=5,AB=13,
∴BC= =12
【分析】因为 △ABC为直角三角形,已知两边的长,运用勾股定理即可直接求出第三边。
四、综合题
10. (1)解: 由题意可知,下一个勾是奇数11, 设斜边和另一条直角边为:m、n, 则m2-n2=112 , 则(m+n)(m-n)=121×1, ∴m+n=121,m-n=1, 解得:m=61, n=60. (2) ; www.21-cn-jy.com
解:(2)设后两个数为:p,q, 且p>q, 由观察可知:则p=q+1, 则n2+q2=(q+1)2 , ∴q=. 则p= 故答案为:,. 【分析】(1)由题意可知下一个奇数为11,设斜边和另一条直角边为m、n,由勾股定理列式,将左式分解因式,结合正整数的特点,求出斜边和直角边分别为61、60. (2)设后两个数为:p,q, 且p>q, 由观察可知p=q+1,根据勾股定理列式,先把q用含n的代数式表示,则p也可用含n的代数式表示.【来源:21·世纪·教育·网】
11. (1)解:在Rt△ABD和Rt△ACD中,
根据勾股定理得:AB2=AD2+BD2 , AC2=AD2+CD2 ,
又AD=12,BD=16,CD=5,
∴AB=20,AC=13,
△ABC的周长=AB+AC+BC=AB+AC+BD+DC=20+13+16+5=54.
(2)解:∵AB=20,AC=13,BC=21,
AB2+AC2≠BC2 ,
∴△ABC不是直角三角形.
【分析】(1)?已知AD、BD、CD,?在Rt△ABD和Rt△ACD中,分别由勾股定理求得AB和AC,BC=BD+DC长度可求,则 △ABC的周长可求; (2)先找出最大边,再求较小两边的平方和,利用勾股定理的逆定理判断即可。
一、单选题
1.如图所示,在Rt△ABC中,∠C=90°,AC=11cm,点P从点A出发沿AC以1cm/s的速度移动,点Q从点C出发沿CB以2cm/s的速度移动,如果P,Q分别从A,C两点同时出发,当它们相距10cm时所需的时间为(?? ) 21世纪教育网版权所有
A.?3s??????????????????????????????????????B.?4s??????????????????????????????????????C.?5s??????????????????????????????????????D.?3s或1.4s
2.下列三条线段能构成直角三角形的是( ??)
A.?6, 7, 8????????????????????????????????B.?2, 3, 4????????????????????????????????C.?3, 4, 6????????????????????????????????D.?6,8, 10
3.在直线l上有三个正方形m、q、n,若m、q的面积分别为5和11,则n的面积( ??)
A.?4??????????????????????????????????????????B.?6??????????????????????????????????????????C.?16??????????????????????????????????????????D.?55
4.将一根长24cm的筷子置于底面直径为5cm,高为12cm的圆柱水杯中,设筷子露在杯子外面的长度为h,则h的取值范围是( ??) 21教育网
A.?12cm≤h≤19cm?????????????B.?12cm≤h≤13cm?????????????C.?11cm≤h≤12cm?????????????D.?5cm≤h≤12cm
二、填空题
5.若直角三角形两条直角边长分别为 和 ,则斜边上的中线长为________.
6.若一直角三角形的两直角边长为 ,1,则斜边长为________.
三、解答题
7.如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则求此时梯顶离路灯的距离。
8.如图,△ABC中,AB=AC , BC=4cm , 作AD⊥BC , 垂足为D , 若AD=4cm , 求AB的长. 21cnjy.com
9.如图,在Rt△ABC中,∠C=90°,AC=5,AB=13,求BC.
四、综合题
10.我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.21·cn·jy·com
(1)请你根据上述的规律写出下一组勾股数:
(2)若第一个数用字母n(n为奇数,且n≥3)表示,那么后两个数用含n的代数式分别表示为________和________,请用所学知识说明它们是一组勾股数. 2·1·c·n·j·y
11.如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5.
求:
(1)△ABC的周长;
(2)判断△ABC是否是直角三角形?为什么?
答案解析部分
一、单选题
1. D
解:设运动时间为ts时PQ=10cm,则CP=(11﹣x)cm,CQ=2xcm,
根据题意得:4x2+(11﹣x)2=100,
解得:x1=1.4,x2=3.
故答案为:D.
【分析】设运动时间为ts时PQ=10cm,根据路程等于速度乘以时间得出AP=tcm,CQ=2tcm,故CP=(11﹣x)cm,根据勾股定理建立方程,求解即可。21·世纪*教育网
2. D
解:A、最大边82=64<62+72=85, 为锐角三角形,A不符合题意; B、最大边42=16>32+22=13, 为钝角三角形,B不符合题意; C、最大边62=36>32+42=25, 为钝角三角形,C不符合题意; C、最大边102=100=62+82=100, 为直角三角形,D不符合题意; 故答案为:D 【分析】先找出最大边,然后根据勾股定理分析判断,最大边的平方小于另外两边的平方和是锐角三角形,等于另外两边的平方和是直角三角形,大于另外两边的平方和是钝角三角形。2-1-c-n-j-y
3. C
∵∠ACB+∠ECD=∠ACB+∠BAC=90°, ∴∠ABC=∠DEC,∠ACB=∠CDE,AC=CD, ∴△ACB≌△△DCE(AAS), ∴AB=CE,BC=DE, 由勾股定理可得,AC2=AB2+BC2=AB2+DE2 Sn=Sm+Sq=11+5=16. n的面积为16 21*cnjy*com
故答案为:C.
【分析】利用全等三角形判定定理证明,再利用勾股定理求得线段的关系,得到面积。
4. C
h最大时为筷子与杯底垂直时,h=12cm 最小时为筷子与杯底和杯高形成直角三角形时,AB= h=24-13=11cm, ∴11cm≤h≤12cm. 【来源:21cnj*y.co*m】
故答案为:C.
【分析】根据题意,找到h最小、最大值的情况,利用勾股定理解答。
二、填空题
5.
解:根据勾股定理,可求得斜边长为 ,所以斜边上的中线长为 .
故答案为: .
【分析】结合题意,由勾股定理即可计算得到斜边的长度,继而计算得到斜边上的中线长即可。
6. 2
解:斜边长= =2,
故答案为:2.
【分析】直接利用勾股定理计算即可.
三、解答题
7. 解:由题意得:BO= B'O=BO+BB'=6+2=8, ∴A'O= ∴AA‘=AO-A'O=8-6=2(米); 故答案为:2米. www-2-1-cnjy-com
【分析】由勾股定理求出BO的长,于是B'D的长可求,在△A'BO中,用勾股定理求出A'D的长,则此时梯顶离路灯的距离可求.【出处:21教育名师】
8. 解:∵AB=AC , BC=4cm , AD⊥BC ,
∴BD= BC=2,
∵AD=4cm ,
∴AB= =2 cm.
【分析】根据等腰三角形三线合一的性质可得BD的长,利用勾股定理求出AB的长即可.
9. 解:∵在Rt△ABC中,∠C=90°,AC=5,AB=13,
∴BC= =12
【分析】因为 △ABC为直角三角形,已知两边的长,运用勾股定理即可直接求出第三边。
四、综合题
10. (1)解: 由题意可知,下一个勾是奇数11, 设斜边和另一条直角边为:m、n, 则m2-n2=112 , 则(m+n)(m-n)=121×1, ∴m+n=121,m-n=1, 解得:m=61, n=60. (2) ; www.21-cn-jy.com
解:(2)设后两个数为:p,q, 且p>q, 由观察可知:则p=q+1, 则n2+q2=(q+1)2 , ∴q=. 则p= 故答案为:,. 【分析】(1)由题意可知下一个奇数为11,设斜边和另一条直角边为m、n,由勾股定理列式,将左式分解因式,结合正整数的特点,求出斜边和直角边分别为61、60. (2)设后两个数为:p,q, 且p>q, 由观察可知p=q+1,根据勾股定理列式,先把q用含n的代数式表示,则p也可用含n的代数式表示.【来源:21·世纪·教育·网】
11. (1)解:在Rt△ABD和Rt△ACD中,
根据勾股定理得:AB2=AD2+BD2 , AC2=AD2+CD2 ,
又AD=12,BD=16,CD=5,
∴AB=20,AC=13,
△ABC的周长=AB+AC+BC=AB+AC+BD+DC=20+13+16+5=54.
(2)解:∵AB=20,AC=13,BC=21,
AB2+AC2≠BC2 ,
∴△ABC不是直角三角形.
【分析】(1)?已知AD、BD、CD,?在Rt△ABD和Rt△ACD中,分别由勾股定理求得AB和AC,BC=BD+DC长度可求,则 △ABC的周长可求; (2)先找出最大边,再求较小两边的平方和,利用勾股定理的逆定理判断即可。
