第14章 勾股定理 单元测试卷(解析版)
文档属性
| 名称 | 第14章 勾股定理 单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 15:20:41 | ||
图片预览


文档简介
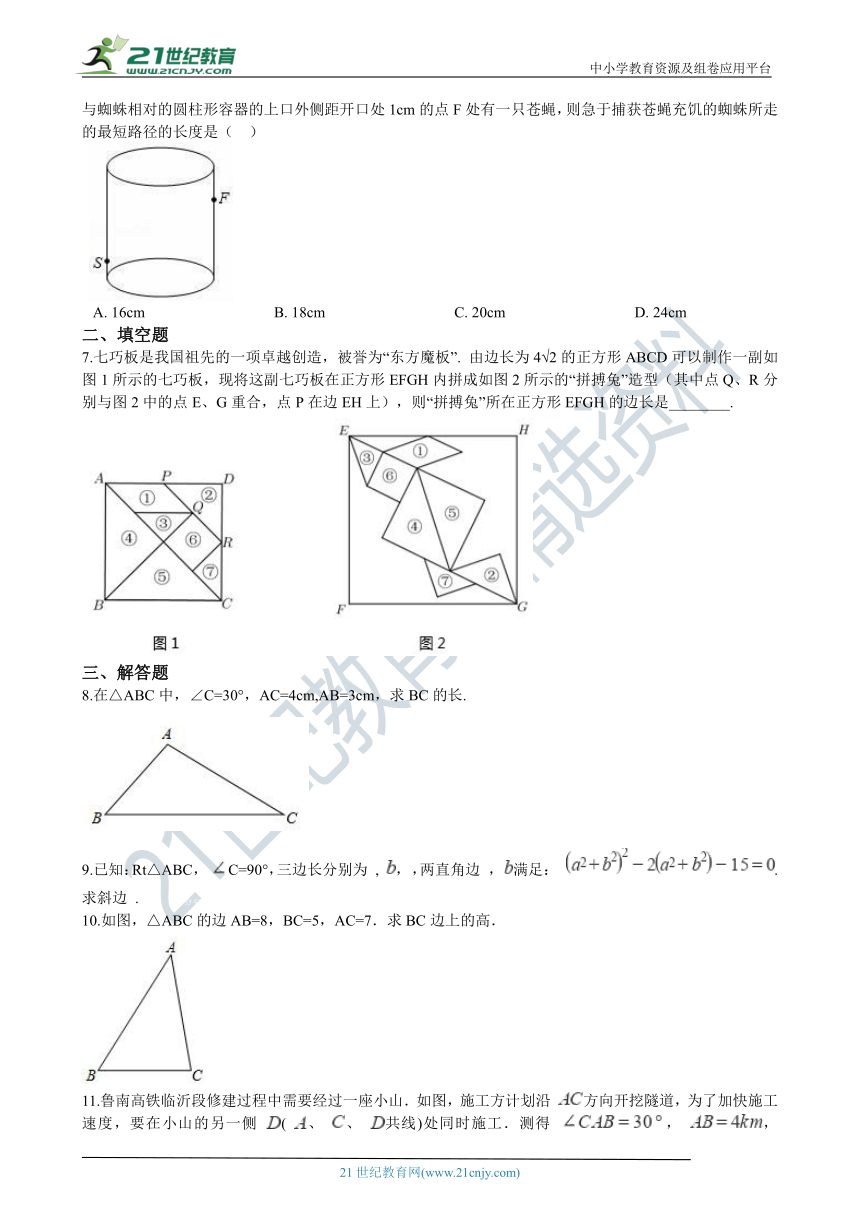
初中数学华师大版八年级上学期 第14章测试卷
一、单选题
1.以下列各组数为边长,能构成直角三角形的是(?? )
A.?2,3,4???????????????????????????B.?3,4,6???????????????????????????C.?5,12,13???????????????????????????D.?1,2,3
2.如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,那么△ABC中BC的高是( ??) 21·cn·jy·com
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
3.下列语句:①每一个外角都等于 的多边形是六边形;②“反证法”就是举反例说明一个命题是假命题;③“等腰三角形两底角相等”的逆命题是真命题;④分式值为零的条件是分子为零且分母不为零,其中正确的个数为(?? ) 2·1·c·n·j·y
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
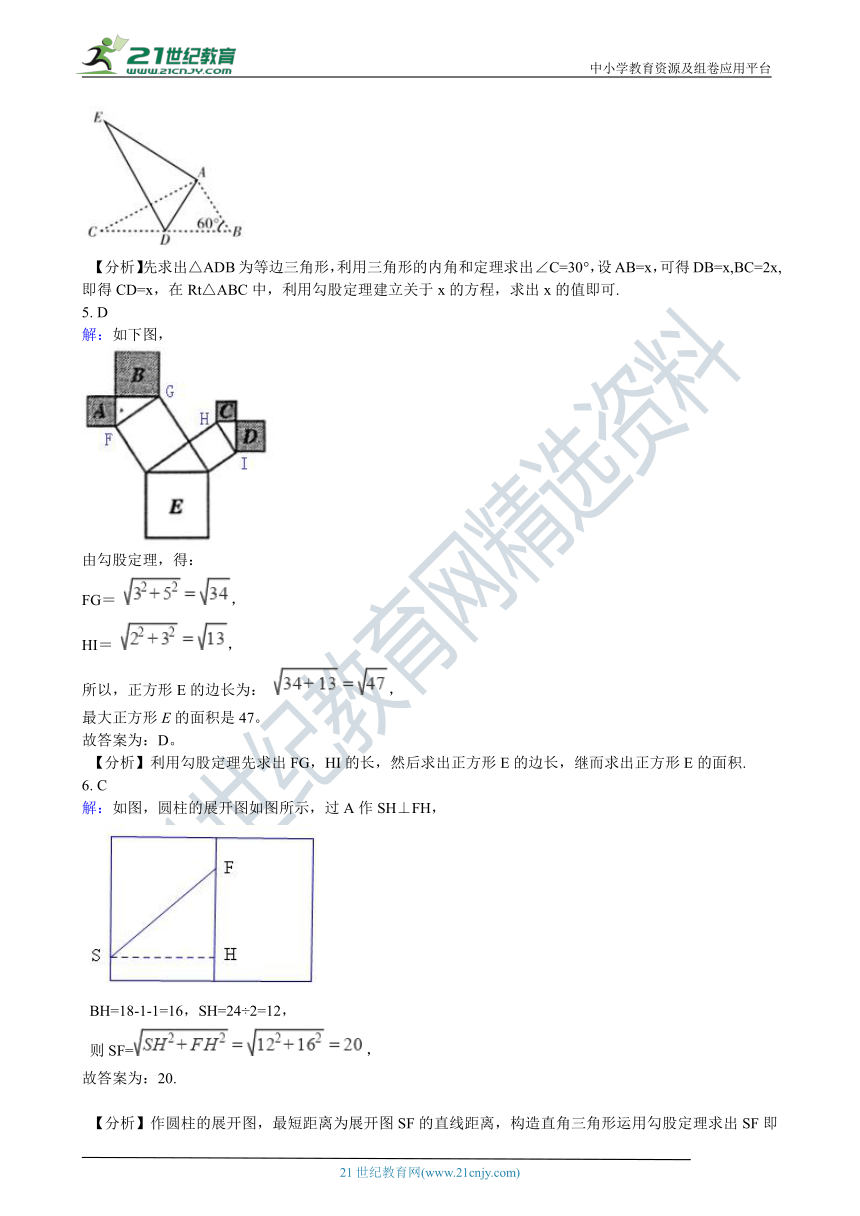
4.如图,将 绕点 按顺时针旋转一定角度得到 ,点 的对应点 恰好落在 边上.若 , ,则 的长为(?? ) 【来源:21·世纪·教育·网】
A.?1???????????????????????????????????????B.????????????????????????????????????????C.?2???????????????????????????????????????D.?
5.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是(?? ) 2-1-c-n-j-y
A.?13?????????????????????????????????????????B.?26?????????????????????????????????????????C.?34?????????????????????????????????????????D.?47
6.如图所示,有一个高18cm,底面周长为24cm的圆柱形玻璃容器,在外侧距下底1cm的点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一只苍蝇,则急于捕获苍蝇充饥的蜘蛛所走的最短路径的长度是( ??) 【出处:21教育名师】
A.?16cm??????????????????????????????????B.?18cm??????????????????????????????????C.?20cm??????????????????????????????????D.?24cm
二、填空题
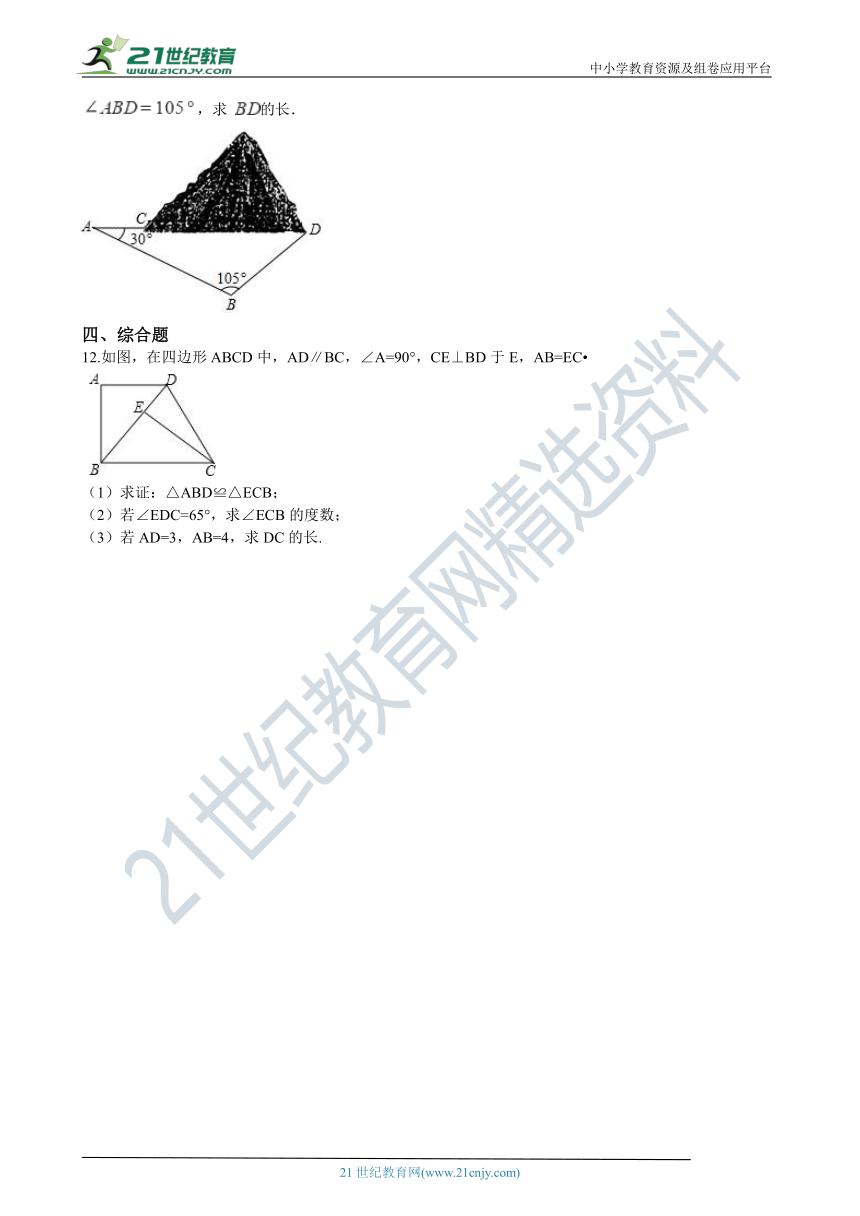
7.七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”. 由边长为4√2的正方形ABCD可以制作一副如图1所示的七巧板,现将这副七巧板在正方形EFGH内拼成如图2所示的“拼搏兔”造型(其中点Q、R分别与图2中的点E、G重合,点P在边EH上),则“拼搏兔”所在正方形EFGH的边长是________.
三、解答题
8.在△ABC中,∠C=30°,AC=4cm,AB=3cm,求BC的长.
9.已知:Rt△ABC, C=90°,三边长分别为 , , ,两直角边 , 满足: .求斜边 . 21cnjy.com
10.如图,△ABC的边AB=8,BC=5,AC=7.求BC边上的高.
11.鲁南高铁临沂段修建过程中需要经过一座小山.如图,施工方计划沿 方向开挖隧道,为了加快施工速度,要在小山的另一侧 ( 、 、 共线)处同时施工.测得 , , ,求 的长.
四、综合题
12.如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC??
(1)求证:△ABD≌△ECB;
(2)若∠EDC=65°,求∠ECB的度数;
(3)若AD=3,AB=4,求DC的长.
答案解析部分
一、单选题
1. C
解:A、22+32=13,42=16,13≠16,
∴2、3、4不能构成直角三角形;
B、32+42=25,62=36,25≠36,
∴3、4、6不能构成直角三角形;
C、∵52+122=169,132=169,169=169,
∴5、12、13能构成直角三角形;
D、∵1+2=3,
∴1、2、3不能构成三角形.
故答案为:C. 【分析】根据勾股定理的逆定理逐一分析判断即可.
2. A
解:S△ABC=2×3-2××1×2-×3×1 =6-2- =. BC= ∴ BC的高为:?. 故答案为:A. ? 21世纪教育网版权所有
【分析】△ABC的面积等于它周围的矩形面积减去其相邻的三个直角三角形面积,据此求出△ABC的面积,再代入面积公式求出BC边上的高即可.21教育网
3. C
解:①每一个外角都等于60°的多边形是六边形,符合题意;
②“反证法”就是从反面的角度思考问题的证明方法,故不符合题意;
③“等腰三角形两底角相等”的逆命题是有两个角相等的三角形为等腰三角形,是真命题,符合题意;
④分式值为零的条件是分子为零且分母不为零,故符合题意;
正确的有3个.
故答案为:C. 【分析】根据多边形的外角,反证法的定义,等腰三角形的性质与判定,分式的值为零的条件分别进行逐一分析即可.21教育名师原创作品
4. C
解:根据题意可知AB=AD,且∠ABD=60°,
∴ 是等边三角形,且 ,
设 ,
则 , ,所以, ,
在 中, ,得, (负值已舍).
故答案为:C.
【分析】先求出△ADB为等边三角形,利用三角形的内角和定理求出∠C=30°,设AB=x,可得DB=x,BC=2x,即得CD=x,在Rt△ABC中,利用勾股定理建立关于x的方程,求出x的值即可.21*cnjy*com
5. D
解:如下图,
由勾股定理,得:
FG= ,
HI= ,
所以,正方形E的边长为: ,
最大正方形E的面积是47。
故答案为:D。 【分析】利用勾股定理先求出FG,HI的长,然后求出正方形E的边长,继而求出正方形E的面积.
6. C
解:如图,圆柱的展开图如图所示,过A作SH⊥FH, BH=18-1-1=16,SH=24÷2=12, 则SF=?, www-2-1-cnjy-com
故答案为:20.
【分析】作圆柱的展开图,最短距离为展开图SF的直线距离,构造直角三角形运用勾股定理求出SF即可。21*cnjy*com
二、填空题
7.
解:如图,延长EO交GH于点K,取②中三角形斜边中点J,连结JK,由图1知KJ一定过②中三角形的直角顶点, 【版权所有:21教育】
由图1可得:
EO=8,OK=2,KJ=4,
∴EK=EO+OK=8+2=10,
在Rt△KGJ中,
∴KG= ,
设正方形EFGH边长为a,则HK=a-2 ,
在Rt△KEH中,
∵EK2=EH2+HK2 ,
即102=a2+(a-2 )2 ,
解得:a=4 或a=-2 (舍去),
∴正方形EFGH边长为4 .
故答案为:4 .
【分析】由图1可得:EO=8,OK=2,KJ=4,EK=10,在Rt△KGJ中,根据勾股定理求得KG长,
设正方形EFGH边长为a,则HK=a-2 ,在Rt△KEH中,根据勾股定理建立一元二次方程,解之即可求得答案.
三、解答题
8. 解:过A点作AD⊥BC,垂足为D,
在Rt△ACD中,
∵ C= :30°,AC=4,
∴AD= AC=2,
∴CD= =2
在Rt△ABD中,
BD= ,
则BC=BD+CD= +2 (cm)
【分析】 添加辅助线过A点作AD⊥BC,垂足为D,将要解决的问题转化为直角三角形中,在Rt△ACD中,利用30°角所对的直角边等于斜边的一半,求出AD的长,利用勾股定理求出CD的长;在Rt△ABD中,利用勾股定理求出BD的长,然后根据BC=BD+CD求出BC的长。www.21-cn-jy.com
9. 解:设这个直角三角形的斜边长是c.
∵a,b分别是一个直角三角形的两直角边的长,
∴a2+b2=c2 ,
又∵(a2+b2)2-2(a2+b2)-15=0,
∴(c2)2-2c2-15=0,
∴(c2-5)(c2+3)=0,
∵c2>0,
∴c2=5,
∵c>0,
∴c= .
即这个直角三角形的斜边长是 .
【分析】根据勾股定理 a2+b2=c2 , 然后利用换元的方法将方程变形为 (c2)2-2c2-15=0, 再利用因式分解法求解并检验即可得出c的值,从而得出答案。21·世纪*教育网
10. 解:作AD⊥BC于D,
由勾股定理得,AD2=AB2-BD2 , AD2=AC2-CD2 ,
∴AB2-BD2=AC2-CD2 , 即82-(5-CD)2=72-CD2 ,
解得,CD=1,
则BC边上的高AD= .
【分析】作AD⊥BC于D,由勾股定理得AD2=AB2-BD2, AD2=AC2-CD2, 从而可得AB2-BD2=AC2-CD2, 即得82-(5-CD)2=72-CD2, 据此求出CD的长,利用勾股定理求出AD的长即可.
11. 解:作 于点 ,
∵ , ,
∴ , ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
即 的长是
【分析】做出辅助线,利用勾股定理,可求得BD的长度。
四、综合题
12. (1)证明:∵AD∥BC,∴∠ADB=∠EBC,
∵∠A=∠CEB=90°,
在△ABD与△CEB中, ,
∴△ABD≌△ECB
(2)解:由(1)证得△ABD≌△ECB,∴BD=BC,
∴∠BCD=∠BDC=65°,
∵∠DCE=90°﹣65°=25°,
∴∠ECB=40°
(3)解: 由(1)证得△ABD≌△ECB,∴CE=AB=4,BE=AD=3,
∴BD=BC= =5,
∴DE=2,
∴CD= =2.
【分析】(1)根据二直线平行,内错角相等得出∠ADB=∠EBC,然后利用AAS判断出△ABD≌△ECB; (2)根据全等三角形的对应边相等得出BD=BC,根据等边对等角得出 ∠BCD=∠BDC=65°, 根据直角三角形的两锐角互余得出 ∠DCE ,根据根据角的和差,由∠ECB=∠DCB-∠DCE即可算出答案; (3) 根据勾股定理算出BD=5,根据全等三角形的对应边相等得出BC=BD=5, AB=EC =4, BE=AB=3, 进而根据边的和差算出DE的长,最后再根据勾股定理算出CD的长.【来源:21cnj*y.co*m】
一、单选题
1.以下列各组数为边长,能构成直角三角形的是(?? )
A.?2,3,4???????????????????????????B.?3,4,6???????????????????????????C.?5,12,13???????????????????????????D.?1,2,3
2.如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,那么△ABC中BC的高是( ??) 21·cn·jy·com
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
3.下列语句:①每一个外角都等于 的多边形是六边形;②“反证法”就是举反例说明一个命题是假命题;③“等腰三角形两底角相等”的逆命题是真命题;④分式值为零的条件是分子为零且分母不为零,其中正确的个数为(?? ) 2·1·c·n·j·y
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
4.如图,将 绕点 按顺时针旋转一定角度得到 ,点 的对应点 恰好落在 边上.若 , ,则 的长为(?? ) 【来源:21·世纪·教育·网】
A.?1???????????????????????????????????????B.????????????????????????????????????????C.?2???????????????????????????????????????D.?
5.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是(?? ) 2-1-c-n-j-y
A.?13?????????????????????????????????????????B.?26?????????????????????????????????????????C.?34?????????????????????????????????????????D.?47
6.如图所示,有一个高18cm,底面周长为24cm的圆柱形玻璃容器,在外侧距下底1cm的点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一只苍蝇,则急于捕获苍蝇充饥的蜘蛛所走的最短路径的长度是( ??) 【出处:21教育名师】
A.?16cm??????????????????????????????????B.?18cm??????????????????????????????????C.?20cm??????????????????????????????????D.?24cm
二、填空题
7.七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”. 由边长为4√2的正方形ABCD可以制作一副如图1所示的七巧板,现将这副七巧板在正方形EFGH内拼成如图2所示的“拼搏兔”造型(其中点Q、R分别与图2中的点E、G重合,点P在边EH上),则“拼搏兔”所在正方形EFGH的边长是________.
三、解答题
8.在△ABC中,∠C=30°,AC=4cm,AB=3cm,求BC的长.
9.已知:Rt△ABC, C=90°,三边长分别为 , , ,两直角边 , 满足: .求斜边 . 21cnjy.com
10.如图,△ABC的边AB=8,BC=5,AC=7.求BC边上的高.
11.鲁南高铁临沂段修建过程中需要经过一座小山.如图,施工方计划沿 方向开挖隧道,为了加快施工速度,要在小山的另一侧 ( 、 、 共线)处同时施工.测得 , , ,求 的长.
四、综合题
12.如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC??
(1)求证:△ABD≌△ECB;
(2)若∠EDC=65°,求∠ECB的度数;
(3)若AD=3,AB=4,求DC的长.
答案解析部分
一、单选题
1. C
解:A、22+32=13,42=16,13≠16,
∴2、3、4不能构成直角三角形;
B、32+42=25,62=36,25≠36,
∴3、4、6不能构成直角三角形;
C、∵52+122=169,132=169,169=169,
∴5、12、13能构成直角三角形;
D、∵1+2=3,
∴1、2、3不能构成三角形.
故答案为:C. 【分析】根据勾股定理的逆定理逐一分析判断即可.
2. A
解:S△ABC=2×3-2××1×2-×3×1 =6-2- =. BC= ∴ BC的高为:?. 故答案为:A. ? 21世纪教育网版权所有
【分析】△ABC的面积等于它周围的矩形面积减去其相邻的三个直角三角形面积,据此求出△ABC的面积,再代入面积公式求出BC边上的高即可.21教育网
3. C
解:①每一个外角都等于60°的多边形是六边形,符合题意;
②“反证法”就是从反面的角度思考问题的证明方法,故不符合题意;
③“等腰三角形两底角相等”的逆命题是有两个角相等的三角形为等腰三角形,是真命题,符合题意;
④分式值为零的条件是分子为零且分母不为零,故符合题意;
正确的有3个.
故答案为:C. 【分析】根据多边形的外角,反证法的定义,等腰三角形的性质与判定,分式的值为零的条件分别进行逐一分析即可.21教育名师原创作品
4. C
解:根据题意可知AB=AD,且∠ABD=60°,
∴ 是等边三角形,且 ,
设 ,
则 , ,所以, ,
在 中, ,得, (负值已舍).
故答案为:C.
【分析】先求出△ADB为等边三角形,利用三角形的内角和定理求出∠C=30°,设AB=x,可得DB=x,BC=2x,即得CD=x,在Rt△ABC中,利用勾股定理建立关于x的方程,求出x的值即可.21*cnjy*com
5. D
解:如下图,
由勾股定理,得:
FG= ,
HI= ,
所以,正方形E的边长为: ,
最大正方形E的面积是47。
故答案为:D。 【分析】利用勾股定理先求出FG,HI的长,然后求出正方形E的边长,继而求出正方形E的面积.
6. C
解:如图,圆柱的展开图如图所示,过A作SH⊥FH, BH=18-1-1=16,SH=24÷2=12, 则SF=?, www-2-1-cnjy-com
故答案为:20.
【分析】作圆柱的展开图,最短距离为展开图SF的直线距离,构造直角三角形运用勾股定理求出SF即可。21*cnjy*com
二、填空题
7.
解:如图,延长EO交GH于点K,取②中三角形斜边中点J,连结JK,由图1知KJ一定过②中三角形的直角顶点, 【版权所有:21教育】
由图1可得:
EO=8,OK=2,KJ=4,
∴EK=EO+OK=8+2=10,
在Rt△KGJ中,
∴KG= ,
设正方形EFGH边长为a,则HK=a-2 ,
在Rt△KEH中,
∵EK2=EH2+HK2 ,
即102=a2+(a-2 )2 ,
解得:a=4 或a=-2 (舍去),
∴正方形EFGH边长为4 .
故答案为:4 .
【分析】由图1可得:EO=8,OK=2,KJ=4,EK=10,在Rt△KGJ中,根据勾股定理求得KG长,
设正方形EFGH边长为a,则HK=a-2 ,在Rt△KEH中,根据勾股定理建立一元二次方程,解之即可求得答案.
三、解答题
8. 解:过A点作AD⊥BC,垂足为D,
在Rt△ACD中,
∵ C= :30°,AC=4,
∴AD= AC=2,
∴CD= =2
在Rt△ABD中,
BD= ,
则BC=BD+CD= +2 (cm)
【分析】 添加辅助线过A点作AD⊥BC,垂足为D,将要解决的问题转化为直角三角形中,在Rt△ACD中,利用30°角所对的直角边等于斜边的一半,求出AD的长,利用勾股定理求出CD的长;在Rt△ABD中,利用勾股定理求出BD的长,然后根据BC=BD+CD求出BC的长。www.21-cn-jy.com
9. 解:设这个直角三角形的斜边长是c.
∵a,b分别是一个直角三角形的两直角边的长,
∴a2+b2=c2 ,
又∵(a2+b2)2-2(a2+b2)-15=0,
∴(c2)2-2c2-15=0,
∴(c2-5)(c2+3)=0,
∵c2>0,
∴c2=5,
∵c>0,
∴c= .
即这个直角三角形的斜边长是 .
【分析】根据勾股定理 a2+b2=c2 , 然后利用换元的方法将方程变形为 (c2)2-2c2-15=0, 再利用因式分解法求解并检验即可得出c的值,从而得出答案。21·世纪*教育网
10. 解:作AD⊥BC于D,
由勾股定理得,AD2=AB2-BD2 , AD2=AC2-CD2 ,
∴AB2-BD2=AC2-CD2 , 即82-(5-CD)2=72-CD2 ,
解得,CD=1,
则BC边上的高AD= .
【分析】作AD⊥BC于D,由勾股定理得AD2=AB2-BD2, AD2=AC2-CD2, 从而可得AB2-BD2=AC2-CD2, 即得82-(5-CD)2=72-CD2, 据此求出CD的长,利用勾股定理求出AD的长即可.
11. 解:作 于点 ,
∵ , ,
∴ , ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
即 的长是
【分析】做出辅助线,利用勾股定理,可求得BD的长度。
四、综合题
12. (1)证明:∵AD∥BC,∴∠ADB=∠EBC,
∵∠A=∠CEB=90°,
在△ABD与△CEB中, ,
∴△ABD≌△ECB
(2)解:由(1)证得△ABD≌△ECB,∴BD=BC,
∴∠BCD=∠BDC=65°,
∵∠DCE=90°﹣65°=25°,
∴∠ECB=40°
(3)解: 由(1)证得△ABD≌△ECB,∴CE=AB=4,BE=AD=3,
∴BD=BC= =5,
∴DE=2,
∴CD= =2.
【分析】(1)根据二直线平行,内错角相等得出∠ADB=∠EBC,然后利用AAS判断出△ABD≌△ECB; (2)根据全等三角形的对应边相等得出BD=BC,根据等边对等角得出 ∠BCD=∠BDC=65°, 根据直角三角形的两锐角互余得出 ∠DCE ,根据根据角的和差,由∠ECB=∠DCB-∠DCE即可算出答案; (3) 根据勾股定理算出BD=5,根据全等三角形的对应边相等得出BC=BD=5, AB=EC =4, BE=AB=3, 进而根据边的和差算出DE的长,最后再根据勾股定理算出CD的长.【来源:21cnj*y.co*m】
