4.6.3 余角和补角 同步练习(解析版)
文档属性
| 名称 | 4.6.3 余角和补角 同步练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 16:43:30 | ||
图片预览

文档简介
初中数学华师大版七年级上学期 第4章 4.6.3 余角和补角
一、单选题
1.已知 ,则 的余角等于(?? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
2.已知 ,则 的补角为(?? )
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
3.已知∠α=60°32’,则∠α的余角是( ??)
A.?29°28’???????????????????????????B.?29°68’???????????????????????????C.?119°28’???????????????????????????D.?119°68’
4.如果一个角的余角是50°,那么这个角的度数是(?? )
A.?30°??????????????????????????????????????B.?40°??????????????????????????????????????C.?50°??????????????????????????????????????D.?130°
5.如图,在?ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( ??)
A.?45°???????????????????????????????????????B.?55°???????????????????????????????????????C.?65°???????????????????????????????????????D.?75°
二、填空题
6.如图,将一块直角三角板的直角顶点放在直尺的一边上,如果∠1=32°,则∠2等于________.
7.如图,AB,CD相交于点O,EO⊥CD,∠AOC=50°,则∠BOE= ________°. 21世纪教育网版权所有
8.如图,两条直线相交成四个角,已知∠2=3∠1,那么∠4=________度。
9.已知一个角的补角比它余角的2倍还大45°,则这个角的度数为________?。
10.如图所示,直线 , 相交于 ,若 ,则 ________度.
三、解答题
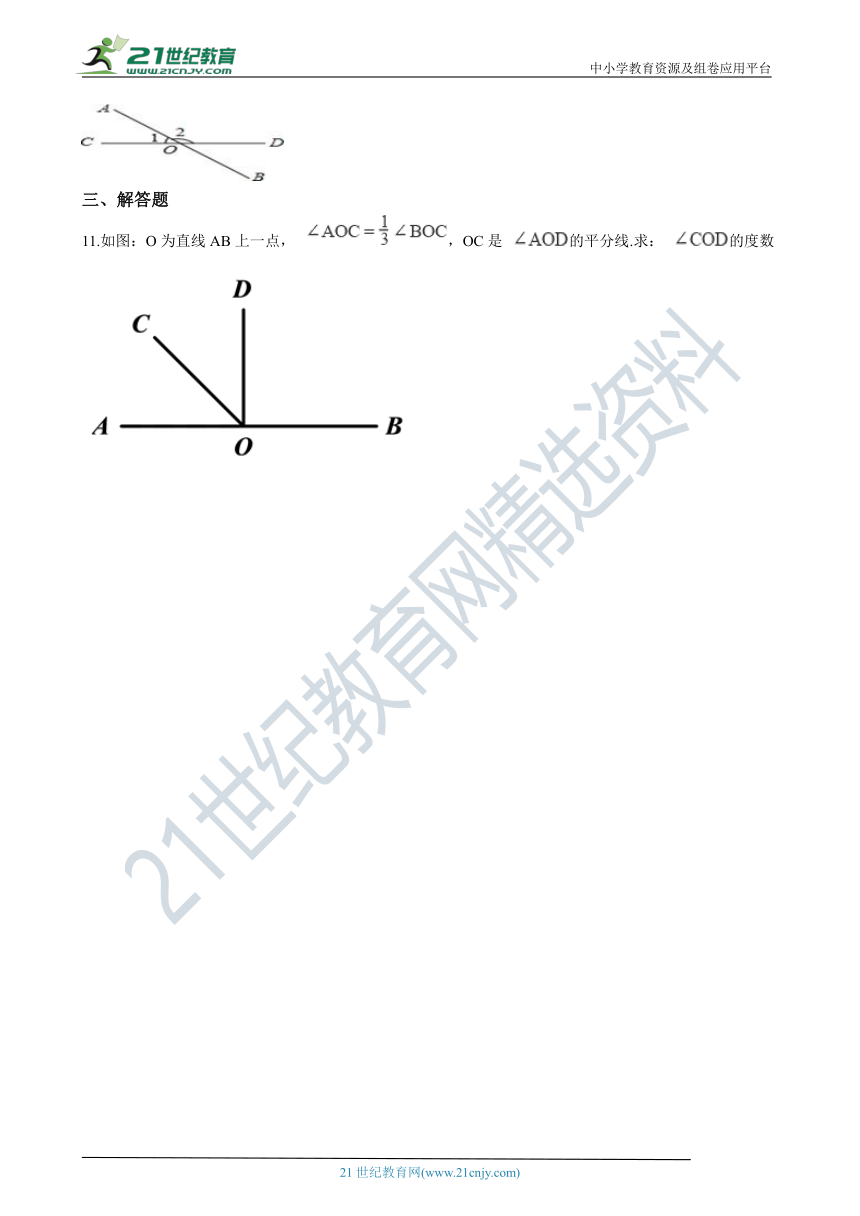
11.如图:O为直线AB上一点, ,OC是 的平分线.求: 的度数
答案解析部分
一、单选题
1. B
解:∵α=60°,
∴α的余角为:90°-α=30°,
故答案为:B.
【分析】如果两个角的和等于90°,那么这两个角是互为余角,其中一个角叫做另一个角的余角,据此解答即可.21cnjy.com
2. C
解:∠A的补角等于:180°-∠A=140°.
故答案为:C.
【分析】若两个角的和等于180°,则这两个角互为补角,据此计算即可.
3. A
解:∵∠α=60°32′,
∴∠α的余角为:90°-60°32′=29°28′.
故答案为:A.
【分析】互余的两个角之和为90°,依此计算即可得出答案.
4. B
解:设这个角为x°,由题意得:
90﹣x=50,
解得:x=40
故答案为:B. 【分析】根据余角的定义从而算出这个角的度数
5. A
根据平行四边形的邻角互补,因为∠A=135°,所以 ?,又因为 ?,所以 ?. 21教育网
故答案为:A. 【分析】根据平行四边形的邻角互补的性质0,可得出∠MCD的度数。
二、填空题
6. 58°
设∠2的补角为x ∠2=180°-x=90°-∠1=58° 【分析】根据平角以及同旁内角互补的关系,可求解。21·cn·jy·com
7. 40
解:∠AOC=∠BOD=50°, ∵ EO⊥CD,?即∠DOE=90°, ∴∠BOE=∠DOE-∠BOD=90°-50°=40°; 故答案为:40. 【分析】∠AOC和∠BOD是对顶角,求得∠AOC,?由EO⊥CD,得∠DOE=90°,由∠BOE等于∠DOE和∠BOD之差,求得∠BOE。www.21-cn-jy.com
8. 135
解∠1+∠2=180°, ∠1+3∠1=180°, 4∠1=180°, ∴∠1=45°, 则∠4=180°-∠1=180°-45°=135°; 故答案为: 135?. ? 2·1·c·n·j·y
【分析】根据邻补角的定义列关系式,求出∠1,再根据邻补角的定义列式求出∠4即可。
9. 45
设这个角的度数为x,则180°-x=2(90°-x)+45° 解得x=45°. 【分析】根据余角和补角的定义,列出方程,解出角的度数。【来源:21·世纪·教育·网】
10. 120
解:∵ ,∠1+∠2=180°,
∴ =180°,
∴ ,
故答案为:120.
【分析】根据邻补角定义可得∠1+∠2=180°,结合已知可求出∠2的度数.
三、解答题
11. 解:∵∠AOC= ∠BOC,∠AOC+∠BOC=180
∴4∠AOC=180 ,∠AOC=45
∵OC平分∠AOD
∴∠COD=∠AOC=45
【分析】利用补角的性质、角平分线的性质,通过计算求解。也可以列一元一次方程求解更容易理解。
一、单选题
1.已知 ,则 的余角等于(?? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
2.已知 ,则 的补角为(?? )
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
3.已知∠α=60°32’,则∠α的余角是( ??)
A.?29°28’???????????????????????????B.?29°68’???????????????????????????C.?119°28’???????????????????????????D.?119°68’
4.如果一个角的余角是50°,那么这个角的度数是(?? )
A.?30°??????????????????????????????????????B.?40°??????????????????????????????????????C.?50°??????????????????????????????????????D.?130°
5.如图,在?ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( ??)
A.?45°???????????????????????????????????????B.?55°???????????????????????????????????????C.?65°???????????????????????????????????????D.?75°
二、填空题
6.如图,将一块直角三角板的直角顶点放在直尺的一边上,如果∠1=32°,则∠2等于________.
7.如图,AB,CD相交于点O,EO⊥CD,∠AOC=50°,则∠BOE= ________°. 21世纪教育网版权所有
8.如图,两条直线相交成四个角,已知∠2=3∠1,那么∠4=________度。
9.已知一个角的补角比它余角的2倍还大45°,则这个角的度数为________?。
10.如图所示,直线 , 相交于 ,若 ,则 ________度.
三、解答题
11.如图:O为直线AB上一点, ,OC是 的平分线.求: 的度数
答案解析部分
一、单选题
1. B
解:∵α=60°,
∴α的余角为:90°-α=30°,
故答案为:B.
【分析】如果两个角的和等于90°,那么这两个角是互为余角,其中一个角叫做另一个角的余角,据此解答即可.21cnjy.com
2. C
解:∠A的补角等于:180°-∠A=140°.
故答案为:C.
【分析】若两个角的和等于180°,则这两个角互为补角,据此计算即可.
3. A
解:∵∠α=60°32′,
∴∠α的余角为:90°-60°32′=29°28′.
故答案为:A.
【分析】互余的两个角之和为90°,依此计算即可得出答案.
4. B
解:设这个角为x°,由题意得:
90﹣x=50,
解得:x=40
故答案为:B. 【分析】根据余角的定义从而算出这个角的度数
5. A
根据平行四边形的邻角互补,因为∠A=135°,所以 ?,又因为 ?,所以 ?. 21教育网
故答案为:A. 【分析】根据平行四边形的邻角互补的性质0,可得出∠MCD的度数。
二、填空题
6. 58°
设∠2的补角为x ∠2=180°-x=90°-∠1=58° 【分析】根据平角以及同旁内角互补的关系,可求解。21·cn·jy·com
7. 40
解:∠AOC=∠BOD=50°, ∵ EO⊥CD,?即∠DOE=90°, ∴∠BOE=∠DOE-∠BOD=90°-50°=40°; 故答案为:40. 【分析】∠AOC和∠BOD是对顶角,求得∠AOC,?由EO⊥CD,得∠DOE=90°,由∠BOE等于∠DOE和∠BOD之差,求得∠BOE。www.21-cn-jy.com
8. 135
解∠1+∠2=180°, ∠1+3∠1=180°, 4∠1=180°, ∴∠1=45°, 则∠4=180°-∠1=180°-45°=135°; 故答案为: 135?. ? 2·1·c·n·j·y
【分析】根据邻补角的定义列关系式,求出∠1,再根据邻补角的定义列式求出∠4即可。
9. 45
设这个角的度数为x,则180°-x=2(90°-x)+45° 解得x=45°. 【分析】根据余角和补角的定义,列出方程,解出角的度数。【来源:21·世纪·教育·网】
10. 120
解:∵ ,∠1+∠2=180°,
∴ =180°,
∴ ,
故答案为:120.
【分析】根据邻补角定义可得∠1+∠2=180°,结合已知可求出∠2的度数.
三、解答题
11. 解:∵∠AOC= ∠BOC,∠AOC+∠BOC=180
∴4∠AOC=180 ,∠AOC=45
∵OC平分∠AOD
∴∠COD=∠AOC=45
【分析】利用补角的性质、角平分线的性质,通过计算求解。也可以列一元一次方程求解更容易理解。
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
