第4节 简单机械 复习(课件 30张ppt)
文档属性
| 名称 | 第4节 简单机械 复习(课件 30张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2019-11-15 00:00:00 | ||
图片预览






文档简介
(共30张PPT)
九上科学复习课件
简单机械
第三章 能量的转化与守恒
考点一:杠杆
五要素:支点、动力、阻力、动力臂、阻力臂
平衡条件:_________
费力杠杆:动力臂_____阻力臂
省力杠杆:动力臂_____阻力臂
等臂杠杆:动力臂_____阻力臂
F1l1=F2l2
小于
大于
等于
第三章 能量的转化与守恒
例题1:
中国人是使用筷子的专家,如图所示,将AB这支筷子作为杠杆分析。O点为支点,食指指头对筷子上的M点压力FM(垂直于筷子)是动力,食物对筷子上N点挤压力FN(垂直于筷子)是阻力,动力FM力臂是( )
OA B.OB
C.OM D.ON
C
第三章 能量的转化与守恒
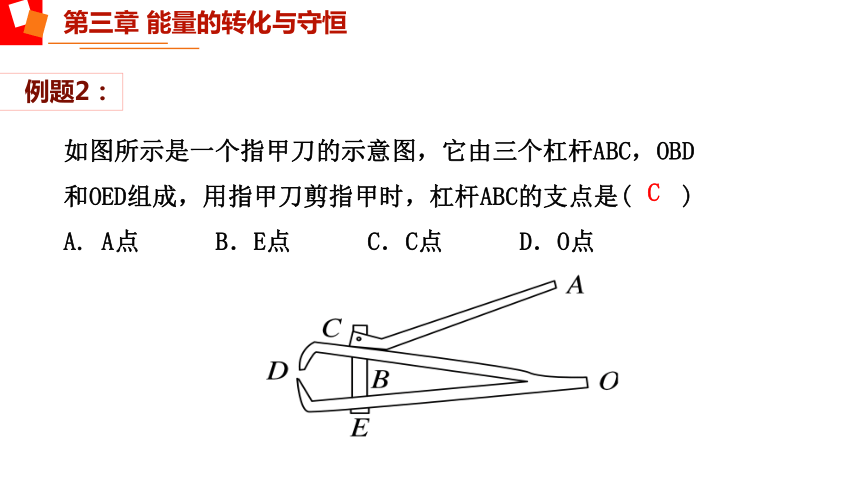
例题2:
如图所示是一个指甲刀的示意图,它由三个杠杆ABC,OBD和OED组成,用指甲刀剪指甲时,杠杆ABC的支点是( )
A. A点 B.E点 C.C点 D.O点
C
第三章 能量的转化与守恒
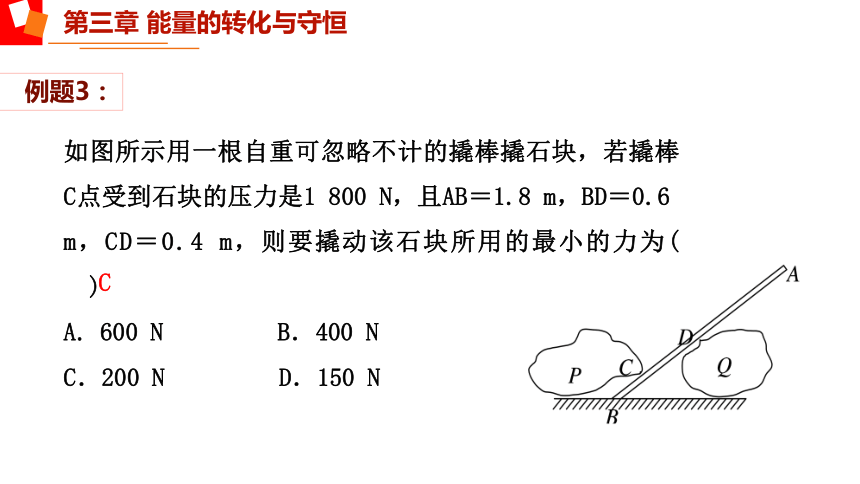
例题3:
如图所示用一根自重可忽略不计的撬棒撬石块,若撬棒C点受到石块的压力是1 800 N,且AB=1.8 m,BD=0.6 m,CD=0.4 m,则要撬动该石块所用的最小的力为( )
600 N B.400 N
C.200 N D.150 N
C
第三章 能量的转化与守恒
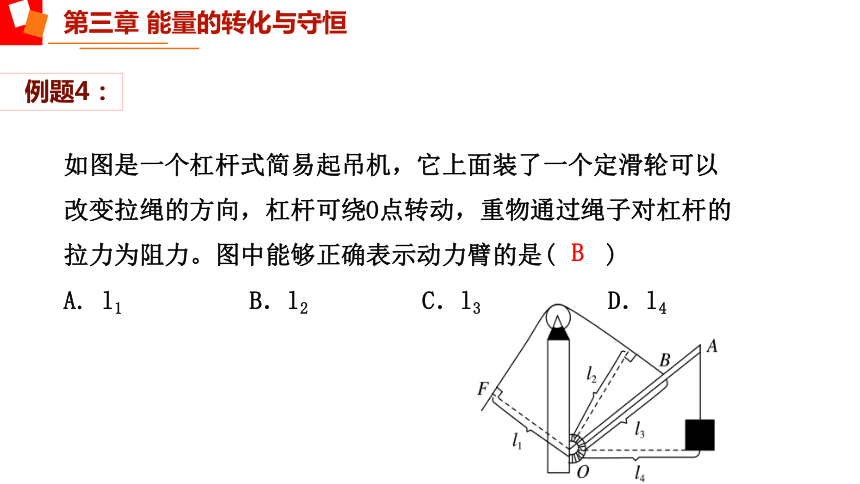
例题4:
B
如图是一个杠杆式简易起吊机,它上面装了一个定滑轮可以改变拉绳的方向,杠杆可绕O点转动,重物通过绳子对杠杆的拉力为阻力。图中能够正确表示动力臂的是( )
A. l1 B.l2 C.l3 D.l4
第三章 能量的转化与守恒
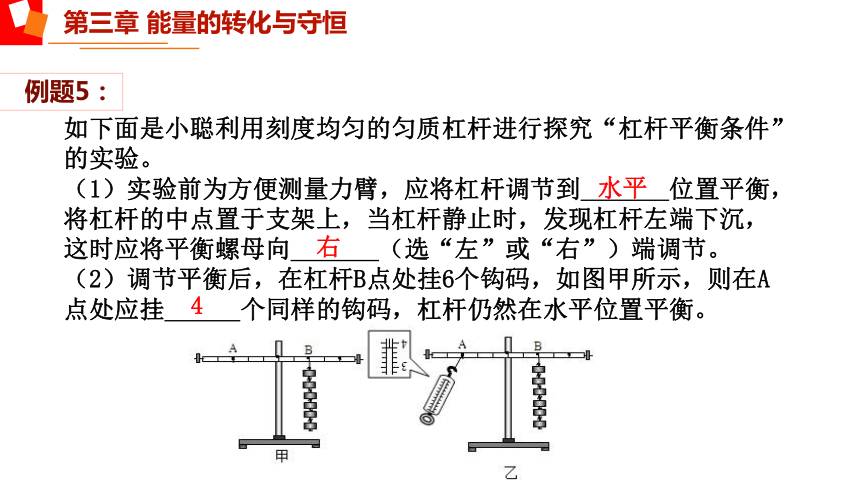
例题5:
水平
如下面是小聪利用刻度均匀的匀质杠杆进行探究“杠杆平衡条件”的实验。
(1)实验前为方便测量力臂,应将杠杆调节到 位置平衡,将杠杆的中点置于支架上,当杠杆静止时,发现杠杆左端下沉,这时应将平衡螺母向 (选“左”或“右”)端调节。
(2)调节平衡后,在杠杆B点处挂6个钩码,如图甲所示,则在A点处应挂 个同样的钩码,杠杆仍然在水平位置平衡。
右
4
第三章 能量的转化与守恒
例题5:
(3)图乙是小聪利用弹簧测力计做的某次实验情景,已知杠杆每格长5cm,钩码每个重0.5N,请将弹簧测力计的示数填入下表。
上述实验数据不符合杠杆平衡条件,出现问题的原因是 。
3.8
弹簧测力计没有竖直向下拉
第三章 能量的转化与守恒
例题6:
如图所示重力不计的木棒AOB可绕支点O无摩擦转动,木棒AB长为3 m,均匀正方体甲的边长为10 cm,物体乙的质量为5.6 kg。当把甲、乙两物体用细绳分别挂在木棒的两个端点A、B上时,木棒在水平位置平衡,此时物体甲对地面的压强为3 000 Pa,支点O距A点1.6 m。求:
(1)物体乙受到的重力;
(2)物体甲受到的支持力;
(3)物体甲的密度。
56N
30N
7.9×103 kg/m3
第三章 能量的转化与守恒
考点二:滑轮
定滑轮:
特点: _____省力、 _____省距离、 _____改变用力的方向
不
不
可以
动滑轮:
特点: _____力、 _____距离、 _____改变用力的方向
省
费
不可以
滑轮组:
特点: _____力、 _____距离、有的 _____改变用力的方向
省
费
可以
省力的机械费距离,费力的机械省距离。
第三章 能量的转化与守恒
考点二:滑轮
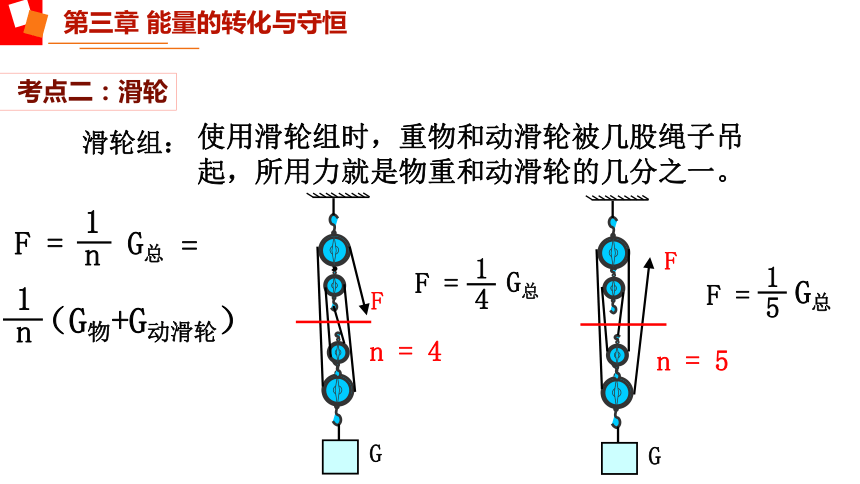
滑轮组:
使用滑轮组时,重物和动滑轮被几股绳子吊
起,所用力就是物重和动滑轮的几分之一。
F =
n
1
=
n
1
(G物+G动滑轮)
G总
G总
F
G
n = 4
F
G
n = 5
F =
4
1
F =
G总
5
1
第三章 能量的转化与守恒
例题1:
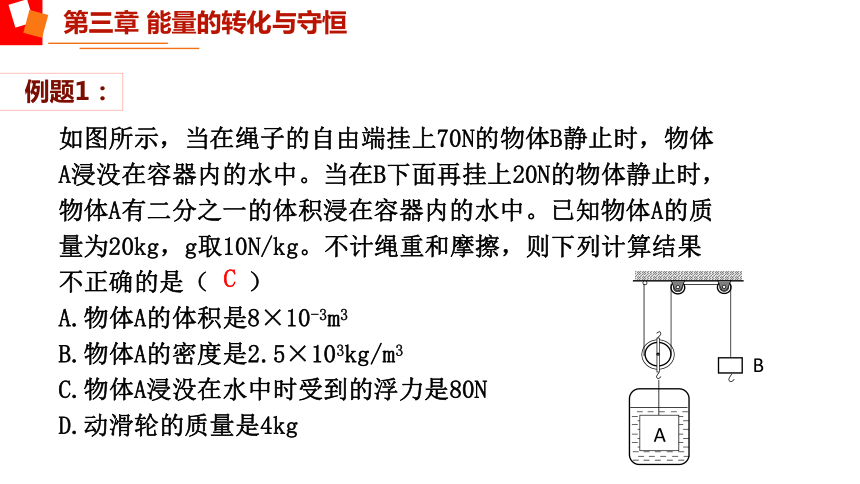
如图所示,当在绳子的自由端挂上70N的物体B静止时,物体A浸没在容器内的水中。当在B下面再挂上20N的物体静止时,物体A有二分之一的体积浸在容器内的水中。已知物体A的质量为20kg,g取10N/kg。不计绳重和摩擦,则下列计算结果不正确的是( )
A.物体A的体积是8×10-3m3
B.物体A的密度是2.5×103kg/m3
C.物体A浸没在水中时受到的浮力是80N
D.动滑轮的质量是4kg
C
A
B
?
第三章 能量的转化与守恒
例题2:
如图所示,体重为510N的人,用滑轮组拉重500N的物体A沿水平方向以0.02m/s的速度匀速运动。运动中物体A受到地面的摩擦阻力为 200N。动滑轮重为20N(不计绳重和摩擦,地面上的定滑轮与物体A相连的绳子沿水平方向,地面上的定滑轮与动滑轮相连的绳子沿竖直方向,人对绳子的拉力与对地面的压力始终竖直向下且在同一直线上,)。则下列计算结果中,正确的是( )
A.绳子自由端受到的拉力大小是100N
B.人对地面的压力为400N
C.人对地面的压力为250N
D.绳子自由端运动速度是0.01m/s
B
A
?
第三章 能量的转化与守恒
例题3:
重为40N的物体A放在水平桌面上,利用图所示的装置使物体A以2m/s 的速度做匀速直线运动,拉力F的大小是2N并保持水平,绳子的伸长及滑轮的摩擦不计。则 ( )
A.拉力F移动的速度是4m/s B.A受到桌面的滑动摩擦力是40N
C.1s内拉力F做的功是4J D.拉力做功的功率是4W
A
第三章 能量的转化与守恒
例题4:
如图所示,用24N的水平拉力F拉滑轮,可以使重20N的物体A以0.2m/s的速度在水平地面上匀速运动。物体B重10N,弹簧测力计的示数为5N且不变。若不计轮重、弹簧测力计重、绳重和轴摩擦则下列说法中正确的是( )
A.地面受到的摩擦力为10N B.滑轮移动的速度为0.4m/s
C.水平拉力F的功率为4.8W D.在2s内绳子对物体A所做的功为4.8J
D
第三章 能量的转化与守恒
考点三:斜面
一种可以省力的简单机械
h
F
A
C
B
L
G
FL
W动力 =
W克服重力=
Gh
W克服摩擦=
fL
f
第三章 能量的转化与守恒
例题1:
某同学家新房装修时,在地面与窗台间放置一斜木板,将瓷砖沿木板从地面匀速拉上窗台。如图所示,已知窗台高3 m,木板长5 m,瓷砖重500 N,沿斜面所用拉力为400 N,则拉力做的功是______,克服重力做的功是______,克服摩擦阻力做功________。
2000J
1500J
500J
第三章 能量的转化与守恒
考点四:有用功、额外功、总功
1.有用功(W有用):
2.额外功(W额外):
3.总功(W总):
即必须要做的功。
即不需要但又不得不做的功。
机械克服摩擦等额外阻力所做的功。
机械克服有用阻力所做的功。
有用功加额外功是总共做的功。
W总 = W有用 + W额外
第三章 能量的转化与守恒
例题1:
建筑工人利用如图所示装置,将质量为100kg的沙袋沿竖直方向从地面匀速提到3m高的二楼楼面,用时30s。已知动滑轮的质量为8kg,不计绳子重力和摩擦。求:
(1)拉力的大小。
(2)这段时间内人拉绳子做的功。
(3)这段时间内人对沙袋做的功。
(4)这段时间内人对动滑轮做的功。
540N
3240J
3000J
240J
第三章 能量的转化与守恒
例题2:
如图所示,用100N的力F将重为150N物体匀速拉到斜面顶部,斜面高h=1m,长S=2m,则人做的有用功是_________,总功是_________。
150J
200J
第三章 能量的转化与守恒
考点五:机械效率
有用功跟总功的比值
1.表达式:
2.η的特点:
(1)无单位
(2)总小于1
(3)一般用百分比表示
η
=
W有用
W总
×100% =
W有用
W有用+W额外
×100%
第三章 能量的转化与守恒
如图所示的滑轮组,用250牛的力提升重为400牛的重物,动滑轮重80牛,要使重物上升3米,求:该滑轮组的机械效率?(摩擦及绳的重力不计)
例题1:
F
G
总功 即拉力所做的功是:
W总 = Fs = 250牛×6米 = 1500焦
有用功 即提升重物所做的功是:
W有 = G物h = 400牛×3米 = 1200焦
η
=
W有用
W总
×100%
=
1200焦
1500焦
×100%=80%
拉力移动距离为 s = 2h = 6米
第三章 能量的转化与守恒
当摩擦及绳的重力不计时:
例题1:
F
G
W总 = Fs = 1/2(G+G滑)×2h=(G+G滑)h
W有用 = Gh
η
=
W有用
W总
×100%
=
Gh
(G+G滑)h
×100%=
G
G+G滑
×100%
第三章 能量的转化与守恒
例题2:
如图所示,用100N的力F将重为150N物体匀速拉到斜面顶部,斜面高h=1m,长S=2m,则机械效率是_________。
75%
如果斜面光滑:FL=Gh
η=100%
如果斜面粗糙:FL=Gh+fL
η=Gh/FL=Gh/(Gh+fL)
第三章 能量的转化与守恒
例题3:
图中定滑轮重2N,动滑轮重1N。物体A在拉力F=4N的作用下,1s内沿竖直方向匀速升高了0.2m。不计绳重和轴摩擦,则以下计算结果正确的是( )
A.绳子自由端移动速度为0.1m/s
B.滑轮组的机械效率为87.5%
C.天花板对滑轮组的拉力为10N
D.滑轮组对物体A做功的功率为1.6W
B
F
第三章 能量的转化与守恒
例题4:
利用如图所示的甲、乙两滑轮组,在相同的时间内用大小相同的力F1和F2分别把质量相等的重物提升到相同的高度,则( )
A.力F2做功的功率大 B.甲滑轮组做的有用功较大 C.甲和乙滑轮组的机械效率相同 D.甲滑轮组做的总功较大
D
乙
F2
G
甲
F1
G
第三章 能量的转化与守恒
例题5:
如图工人们用滑轮组匀速提起水池中体积为0.1m3、密度为2.7×103kg/m3的实心金属块,在10s内竖直上升了0.5m(金属块始终浸没在水中),水面到池底深度为12m(ρ水=1.0×103kg/m3,g=10N/kg)求:
(1)水池底部受到水的压强;
(2)金属块受到的浮力大小;
(3)若不计摩擦、绳子和动滑轮的重力,则作用于绳子末端的力为多大?
(4)若实际所用拉力为1000N,则这个滑轮组的机械效率为多大?
1.2×105Pa
1000N
850N
85%
第三章 能量的转化与守恒
例题5:
(1)水池底部受到水的压强:p=ρ水gh=1.0×103kg/m3×10N/kg×12m=1.2×105Pa;
(2)因为金属块浸没在水中,所以排开水的体积:V排=V=0.1m3,
金属块受到的浮力:F浮=ρ水gV排=1×103kg/m3×10N/kg×0.1m3=1000N;
第三章 能量的转化与守恒
例题5:
(3)由ρ=m/V得金属块的质量:m=ρ铝V=2.7×103kg/m3×0.1m3=270kg,金属块的重力:G=mg=270kg×10N/kg=2700N;由图可知,n=2,不计摩擦、绳子和动滑轮的重力,拉力:F=1/2(G﹣F浮)=1/2(2700N﹣1000N)=850N;
(4)由图知,n=2,绳端移动距离s=2h′=2×0.5m=1m,若实际所用拉力为1000N,则总功为:W总=Fs=1000N×1m=1000J,使用滑轮组所做的有用功:W有用=(G﹣F浮)h=(2700N﹣1000N)×0.5m=850J,
此时该滑轮组的机械效率:η= W有用/ W总= 850J/ 1000J×100%=85%。
第三章 能量的转化与守恒
考点五:机械效率
提高机械效率的方法:
(1)减小摩擦,经常润滑,定时保养。
(2)减小机械本身的重力。
1、在使用机械时,尽可能减小额外功。
影响滑轮组的机械效率的主要因素有:动滑轮重、摩擦、物重。
影响斜面的机械效率的主要因素有:倾斜角度、接触面粗糙程度。
2、在额外功一定时,增大有用功.
九上科学复习课件
简单机械
第三章 能量的转化与守恒
考点一:杠杆
五要素:支点、动力、阻力、动力臂、阻力臂
平衡条件:_________
费力杠杆:动力臂_____阻力臂
省力杠杆:动力臂_____阻力臂
等臂杠杆:动力臂_____阻力臂
F1l1=F2l2
小于
大于
等于
第三章 能量的转化与守恒
例题1:
中国人是使用筷子的专家,如图所示,将AB这支筷子作为杠杆分析。O点为支点,食指指头对筷子上的M点压力FM(垂直于筷子)是动力,食物对筷子上N点挤压力FN(垂直于筷子)是阻力,动力FM力臂是( )
OA B.OB
C.OM D.ON
C
第三章 能量的转化与守恒
例题2:
如图所示是一个指甲刀的示意图,它由三个杠杆ABC,OBD和OED组成,用指甲刀剪指甲时,杠杆ABC的支点是( )
A. A点 B.E点 C.C点 D.O点
C
第三章 能量的转化与守恒
例题3:
如图所示用一根自重可忽略不计的撬棒撬石块,若撬棒C点受到石块的压力是1 800 N,且AB=1.8 m,BD=0.6 m,CD=0.4 m,则要撬动该石块所用的最小的力为( )
600 N B.400 N
C.200 N D.150 N
C
第三章 能量的转化与守恒
例题4:
B
如图是一个杠杆式简易起吊机,它上面装了一个定滑轮可以改变拉绳的方向,杠杆可绕O点转动,重物通过绳子对杠杆的拉力为阻力。图中能够正确表示动力臂的是( )
A. l1 B.l2 C.l3 D.l4
第三章 能量的转化与守恒
例题5:
水平
如下面是小聪利用刻度均匀的匀质杠杆进行探究“杠杆平衡条件”的实验。
(1)实验前为方便测量力臂,应将杠杆调节到 位置平衡,将杠杆的中点置于支架上,当杠杆静止时,发现杠杆左端下沉,这时应将平衡螺母向 (选“左”或“右”)端调节。
(2)调节平衡后,在杠杆B点处挂6个钩码,如图甲所示,则在A点处应挂 个同样的钩码,杠杆仍然在水平位置平衡。
右
4
第三章 能量的转化与守恒
例题5:
(3)图乙是小聪利用弹簧测力计做的某次实验情景,已知杠杆每格长5cm,钩码每个重0.5N,请将弹簧测力计的示数填入下表。
上述实验数据不符合杠杆平衡条件,出现问题的原因是 。
3.8
弹簧测力计没有竖直向下拉
第三章 能量的转化与守恒
例题6:
如图所示重力不计的木棒AOB可绕支点O无摩擦转动,木棒AB长为3 m,均匀正方体甲的边长为10 cm,物体乙的质量为5.6 kg。当把甲、乙两物体用细绳分别挂在木棒的两个端点A、B上时,木棒在水平位置平衡,此时物体甲对地面的压强为3 000 Pa,支点O距A点1.6 m。求:
(1)物体乙受到的重力;
(2)物体甲受到的支持力;
(3)物体甲的密度。
56N
30N
7.9×103 kg/m3
第三章 能量的转化与守恒
考点二:滑轮
定滑轮:
特点: _____省力、 _____省距离、 _____改变用力的方向
不
不
可以
动滑轮:
特点: _____力、 _____距离、 _____改变用力的方向
省
费
不可以
滑轮组:
特点: _____力、 _____距离、有的 _____改变用力的方向
省
费
可以
省力的机械费距离,费力的机械省距离。
第三章 能量的转化与守恒
考点二:滑轮
滑轮组:
使用滑轮组时,重物和动滑轮被几股绳子吊
起,所用力就是物重和动滑轮的几分之一。
F =
n
1
=
n
1
(G物+G动滑轮)
G总
G总
F
G
n = 4
F
G
n = 5
F =
4
1
F =
G总
5
1
第三章 能量的转化与守恒
例题1:
如图所示,当在绳子的自由端挂上70N的物体B静止时,物体A浸没在容器内的水中。当在B下面再挂上20N的物体静止时,物体A有二分之一的体积浸在容器内的水中。已知物体A的质量为20kg,g取10N/kg。不计绳重和摩擦,则下列计算结果不正确的是( )
A.物体A的体积是8×10-3m3
B.物体A的密度是2.5×103kg/m3
C.物体A浸没在水中时受到的浮力是80N
D.动滑轮的质量是4kg
C
A
B
?
第三章 能量的转化与守恒
例题2:
如图所示,体重为510N的人,用滑轮组拉重500N的物体A沿水平方向以0.02m/s的速度匀速运动。运动中物体A受到地面的摩擦阻力为 200N。动滑轮重为20N(不计绳重和摩擦,地面上的定滑轮与物体A相连的绳子沿水平方向,地面上的定滑轮与动滑轮相连的绳子沿竖直方向,人对绳子的拉力与对地面的压力始终竖直向下且在同一直线上,)。则下列计算结果中,正确的是( )
A.绳子自由端受到的拉力大小是100N
B.人对地面的压力为400N
C.人对地面的压力为250N
D.绳子自由端运动速度是0.01m/s
B
A
?
第三章 能量的转化与守恒
例题3:
重为40N的物体A放在水平桌面上,利用图所示的装置使物体A以2m/s 的速度做匀速直线运动,拉力F的大小是2N并保持水平,绳子的伸长及滑轮的摩擦不计。则 ( )
A.拉力F移动的速度是4m/s B.A受到桌面的滑动摩擦力是40N
C.1s内拉力F做的功是4J D.拉力做功的功率是4W
A
第三章 能量的转化与守恒
例题4:
如图所示,用24N的水平拉力F拉滑轮,可以使重20N的物体A以0.2m/s的速度在水平地面上匀速运动。物体B重10N,弹簧测力计的示数为5N且不变。若不计轮重、弹簧测力计重、绳重和轴摩擦则下列说法中正确的是( )
A.地面受到的摩擦力为10N B.滑轮移动的速度为0.4m/s
C.水平拉力F的功率为4.8W D.在2s内绳子对物体A所做的功为4.8J
D
第三章 能量的转化与守恒
考点三:斜面
一种可以省力的简单机械
h
F
A
C
B
L
G
FL
W动力 =
W克服重力=
Gh
W克服摩擦=
fL
f
第三章 能量的转化与守恒
例题1:
某同学家新房装修时,在地面与窗台间放置一斜木板,将瓷砖沿木板从地面匀速拉上窗台。如图所示,已知窗台高3 m,木板长5 m,瓷砖重500 N,沿斜面所用拉力为400 N,则拉力做的功是______,克服重力做的功是______,克服摩擦阻力做功________。
2000J
1500J
500J
第三章 能量的转化与守恒
考点四:有用功、额外功、总功
1.有用功(W有用):
2.额外功(W额外):
3.总功(W总):
即必须要做的功。
即不需要但又不得不做的功。
机械克服摩擦等额外阻力所做的功。
机械克服有用阻力所做的功。
有用功加额外功是总共做的功。
W总 = W有用 + W额外
第三章 能量的转化与守恒
例题1:
建筑工人利用如图所示装置,将质量为100kg的沙袋沿竖直方向从地面匀速提到3m高的二楼楼面,用时30s。已知动滑轮的质量为8kg,不计绳子重力和摩擦。求:
(1)拉力的大小。
(2)这段时间内人拉绳子做的功。
(3)这段时间内人对沙袋做的功。
(4)这段时间内人对动滑轮做的功。
540N
3240J
3000J
240J
第三章 能量的转化与守恒
例题2:
如图所示,用100N的力F将重为150N物体匀速拉到斜面顶部,斜面高h=1m,长S=2m,则人做的有用功是_________,总功是_________。
150J
200J
第三章 能量的转化与守恒
考点五:机械效率
有用功跟总功的比值
1.表达式:
2.η的特点:
(1)无单位
(2)总小于1
(3)一般用百分比表示
η
=
W有用
W总
×100% =
W有用
W有用+W额外
×100%
第三章 能量的转化与守恒
如图所示的滑轮组,用250牛的力提升重为400牛的重物,动滑轮重80牛,要使重物上升3米,求:该滑轮组的机械效率?(摩擦及绳的重力不计)
例题1:
F
G
总功 即拉力所做的功是:
W总 = Fs = 250牛×6米 = 1500焦
有用功 即提升重物所做的功是:
W有 = G物h = 400牛×3米 = 1200焦
η
=
W有用
W总
×100%
=
1200焦
1500焦
×100%=80%
拉力移动距离为 s = 2h = 6米
第三章 能量的转化与守恒
当摩擦及绳的重力不计时:
例题1:
F
G
W总 = Fs = 1/2(G+G滑)×2h=(G+G滑)h
W有用 = Gh
η
=
W有用
W总
×100%
=
Gh
(G+G滑)h
×100%=
G
G+G滑
×100%
第三章 能量的转化与守恒
例题2:
如图所示,用100N的力F将重为150N物体匀速拉到斜面顶部,斜面高h=1m,长S=2m,则机械效率是_________。
75%
如果斜面光滑:FL=Gh
η=100%
如果斜面粗糙:FL=Gh+fL
η=Gh/FL=Gh/(Gh+fL)
第三章 能量的转化与守恒
例题3:
图中定滑轮重2N,动滑轮重1N。物体A在拉力F=4N的作用下,1s内沿竖直方向匀速升高了0.2m。不计绳重和轴摩擦,则以下计算结果正确的是( )
A.绳子自由端移动速度为0.1m/s
B.滑轮组的机械效率为87.5%
C.天花板对滑轮组的拉力为10N
D.滑轮组对物体A做功的功率为1.6W
B
F
第三章 能量的转化与守恒
例题4:
利用如图所示的甲、乙两滑轮组,在相同的时间内用大小相同的力F1和F2分别把质量相等的重物提升到相同的高度,则( )
A.力F2做功的功率大 B.甲滑轮组做的有用功较大 C.甲和乙滑轮组的机械效率相同 D.甲滑轮组做的总功较大
D
乙
F2
G
甲
F1
G
第三章 能量的转化与守恒
例题5:
如图工人们用滑轮组匀速提起水池中体积为0.1m3、密度为2.7×103kg/m3的实心金属块,在10s内竖直上升了0.5m(金属块始终浸没在水中),水面到池底深度为12m(ρ水=1.0×103kg/m3,g=10N/kg)求:
(1)水池底部受到水的压强;
(2)金属块受到的浮力大小;
(3)若不计摩擦、绳子和动滑轮的重力,则作用于绳子末端的力为多大?
(4)若实际所用拉力为1000N,则这个滑轮组的机械效率为多大?
1.2×105Pa
1000N
850N
85%
第三章 能量的转化与守恒
例题5:
(1)水池底部受到水的压强:p=ρ水gh=1.0×103kg/m3×10N/kg×12m=1.2×105Pa;
(2)因为金属块浸没在水中,所以排开水的体积:V排=V=0.1m3,
金属块受到的浮力:F浮=ρ水gV排=1×103kg/m3×10N/kg×0.1m3=1000N;
第三章 能量的转化与守恒
例题5:
(3)由ρ=m/V得金属块的质量:m=ρ铝V=2.7×103kg/m3×0.1m3=270kg,金属块的重力:G=mg=270kg×10N/kg=2700N;由图可知,n=2,不计摩擦、绳子和动滑轮的重力,拉力:F=1/2(G﹣F浮)=1/2(2700N﹣1000N)=850N;
(4)由图知,n=2,绳端移动距离s=2h′=2×0.5m=1m,若实际所用拉力为1000N,则总功为:W总=Fs=1000N×1m=1000J,使用滑轮组所做的有用功:W有用=(G﹣F浮)h=(2700N﹣1000N)×0.5m=850J,
此时该滑轮组的机械效率:η= W有用/ W总= 850J/ 1000J×100%=85%。
第三章 能量的转化与守恒
考点五:机械效率
提高机械效率的方法:
(1)减小摩擦,经常润滑,定时保养。
(2)减小机械本身的重力。
1、在使用机械时,尽可能减小额外功。
影响滑轮组的机械效率的主要因素有:动滑轮重、摩擦、物重。
影响斜面的机械效率的主要因素有:倾斜角度、接触面粗糙程度。
2、在额外功一定时,增大有用功.
同课章节目录
- 第1章 物质及其变化
- 第1节 物质的变化
- 第2节 物质的酸碱性
- 第3节 常见的酸
- 第4节 常见的碱
- 第5节 酸和碱之间发生的反应
- 第6节 几种重要的盐
- 第2章 物质转化与材料利用
- 第1节 金属材料
- 第2节 金属的化学性质
- 第3节 有机物和有机合成材料
- 第4节 物质的分类
- 第5节 物质的转化
- 第6节 材料的利用与发展
- 第3章 能量的转化与守恒
- 第1节 能量及其形式
- 第2节 机械能
- 第3节 能量转化的量度
- 第4节 简单机械
- 第5节 物体的内能
- 第6节 电能
- 第7节 核能
- 第8节 能量的转化与守恒
- 第4章 代谢与平衡
- 第1节 食物与营养
- 第2节 食物的消化与吸收
- 第3节 体内物质的运输
- 第4节 能量的获得
- 第5节 体内物质的动态平衡
- 研究性学习课题
- 一 当地酸雨情况以及对农作物和建筑物的影响
- 二 金属对社会发展的作用
- 三 寻找自行车中的杠杆
- 四 怎样防治龋齿
