4.3 角课件

(共39张PPT)
北师大版 七年级
3 角
有公共端点的两条射线组成的图形叫做角.
角的概念：
这两条射线的公共端点是这个角的顶点.
这两条射线是这个角的两条边.




顶点
边
边
角也可以看成是由一条射线绕着它的端点旋转而成的。

始边
终边
顶点
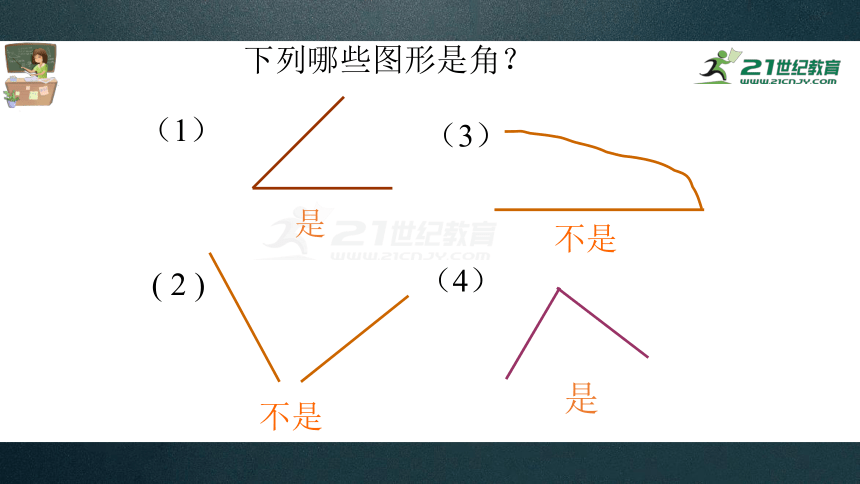
下列哪些图形是角？
（1）


( 2 )


（3）
（4）




是
是
不是
不是





O
B
A
一条射线绕它的端点旋转，当终边和始边成一条直线时，所成的角叫做平角.



O
A
（B）
终边继续旋转，当它有和始边重合时，所成的角叫做周角.
再看两种特殊情况:
在不做特别说明的情况下，我们说的角都指不大于平角的角

A
O
B
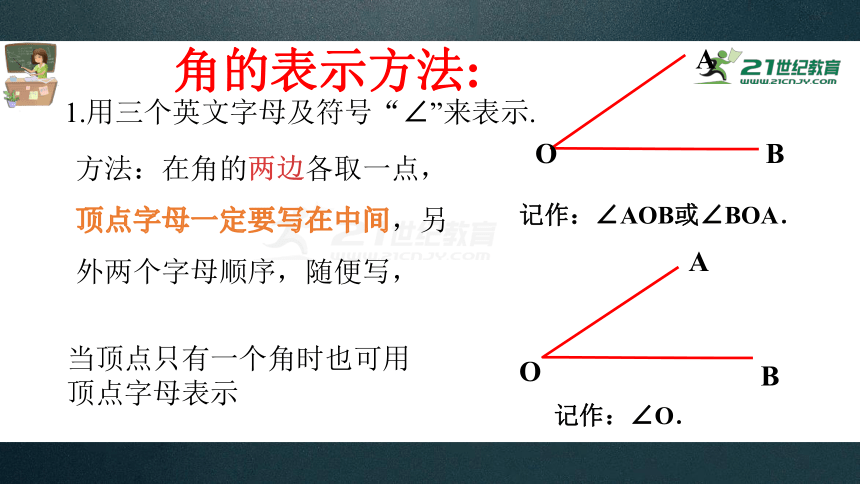
记作：∠AOB或∠BOA．

A
O
B
记作：∠O．
1.用三个英文字母及符号“∠”来表示.
方法：在角的两边各取一点，顶点字母一定要写在中间，另外两个字母顺序，随便写，
当顶点只有一个角时也可用顶点字母表示
角的表示方法:


B
A
C


B
A
D

C
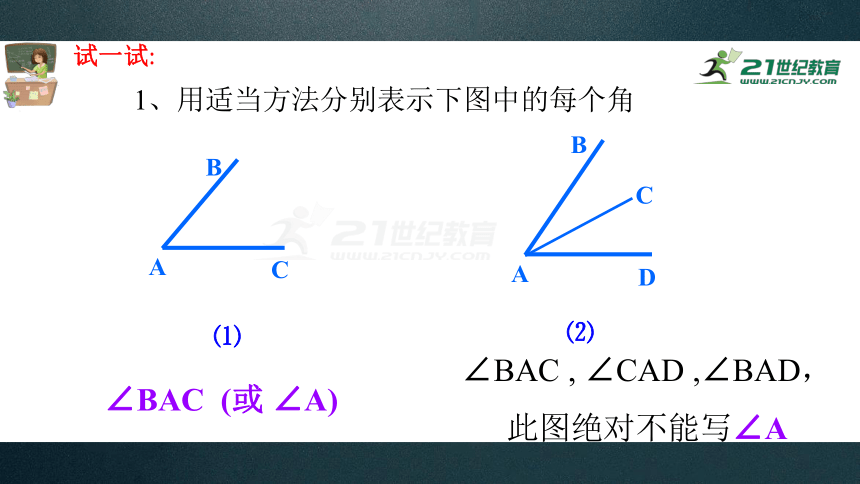
试一试:
⑴
⑵
1、用适当方法分别表示下图中的每个角
∠BAC (或 ∠A)
∠BAC , ∠CAD ,∠BAD，
此图绝对不能写∠A
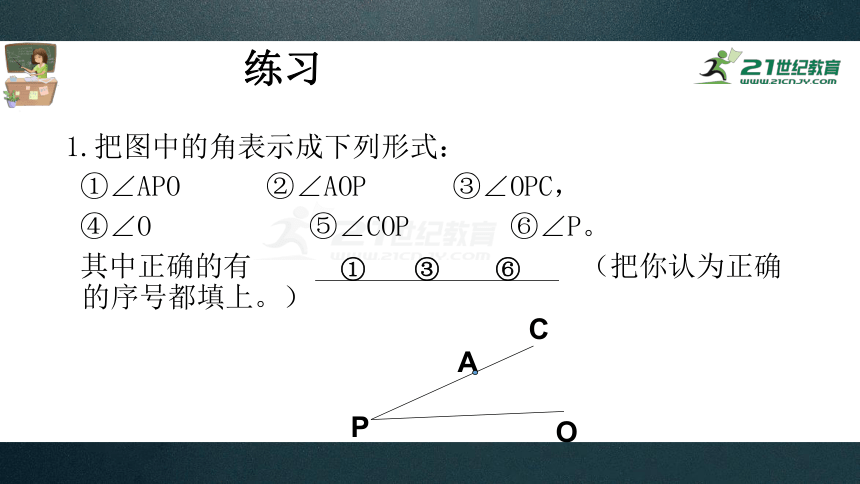
练习
1.把图中的角表示成下列形式：
①∠APO ②∠AOP ③∠OPC，
④∠O ⑤∠COP ⑥∠P。
其中正确的有 （把你认为正确的序号都填上。）



P
O
A
C


① ③ ⑥


α

记作：∠α．∠β，∠θ


1


记作：∠1．
3.用一个数字1、2、3、4等及符号“∠”来表示
2.用一个希腊字母α、β、γ、θ等
及符号“∠” 来表示.


B
A
D

C



记作：∠1．∠2
∠BAD
β

θ
1
2
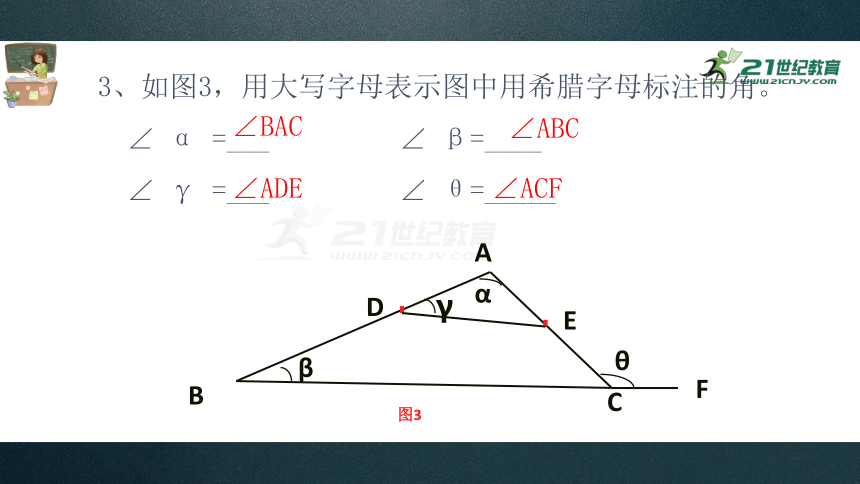
3、如图3，用大写字母表示图中用希腊字母标注的角。
∠ α =___ ∠ β=____
∠ γ =___ ∠ θ=_____



A
C
B
图3
D
E






F




γ
β
α
θ
∠BAC
∠ADE
∠ABC
∠ACF


A
B
C
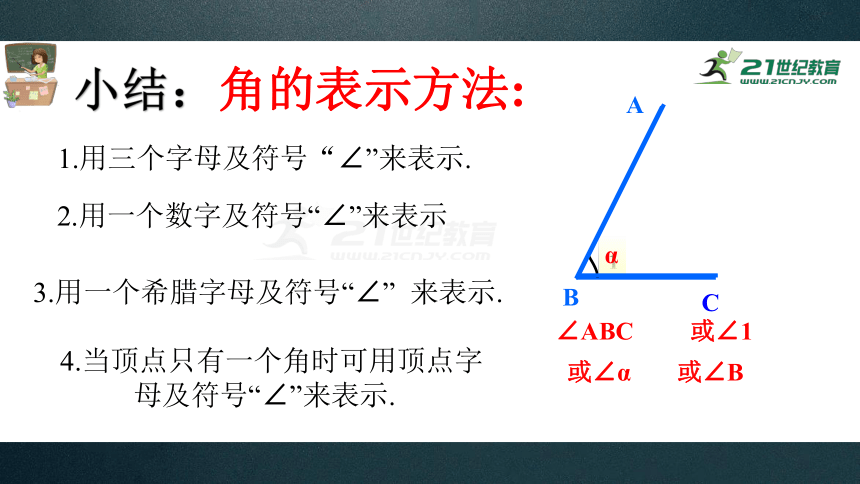
1.用三个字母及符号“∠”来表示.
小结：角的表示方法:
2.用一个数字及符号“∠”来表示
∠ABC
或∠1

1
或∠α
α


3.用一个希腊字母及符号“∠” 来表示.
4.当顶点只有一个角时可用顶点字母及符号“∠”来表示.
或∠B

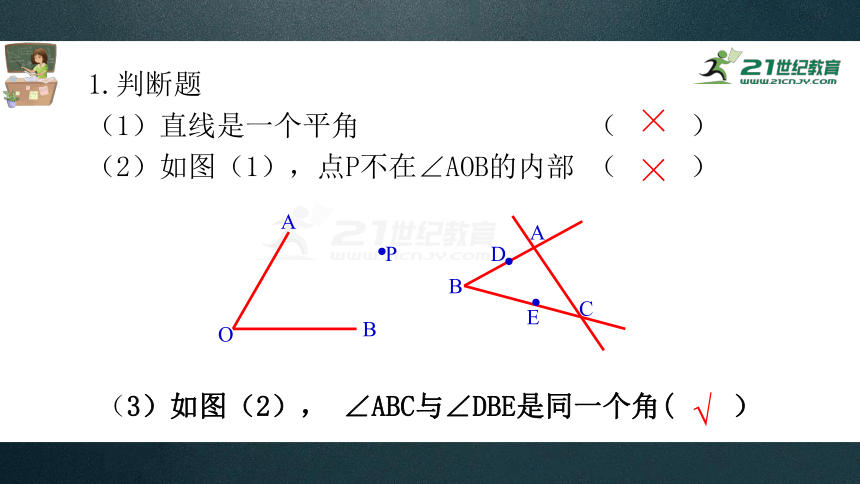
1.判断题
（1）直线是一个平角 （ ）
（2）如图（1），点P不在∠AOB的内部 （ ）


A
O
B
·
P



A
B
C
·
·
D
E
（3）如图（2）， ∠ABC与∠DBE是同一个角( ）
×
×
√
2.将图中的角用不同的方法表示出来，并填写下表：
∠1 ∠3 ∠4
∠ACB ∠ABC
A
D
C



B
E





5
4
3
1
2

∠BCE
∠2

∠BAC
∠DAB
∠5

练一练
C
D
B
A




（1）∠ABD与∠ABC是同一个角吗？
（2）能用一个大写字母表示的角有几个？
（3）以点A为顶点的角有哪几个？
以点D为顶点的角呢？　　　　　
（4）图中共有多少个角？是哪些角？
2个（∠B和∠C）
是
3个∠BAD,∠DAC,∠BAC
2个∠BDA,∠ADC
7个


A
B
C
1.用三个字母及符号“∠”来表示.
角的表示方法:
2.用一个数字及符号“∠”来表示
∠ABC
或∠1

1
或∠α
α


3.用一个希腊字母及符号“∠” 来表示.
4.当顶点只有一个角时可用顶点字母及符号“∠”来表示.
或∠B

有公共端点的两条射线组成的图形叫做角.
小结：
作业布置
完成习题4.3问题解决
4.3角
第二课时，角度计算
把1分的角60等分，每一份所对的角叫做 1 秒的角．记作 “1″ ” 。
把1度的角60等分，每一份所对的角叫做 1 分的角．记作 “1′ ” 。
把一平角分成180等分，每一份所对的角叫做1度的角，记作 “1°” 。
角的 度量
1度=60分 1°＝60 ′
1分=60秒 １′＝60″
1秒= 度 1 ′＝（ ）°
1秒= 分 １″＝（ ）′




归纳
1度=60分； 1分=60秒；1度= 秒
1分= 度； 1秒= 分；1秒= 度
1°＝60 ′ 1′＝60″．

1 ″ ＝ ′ 1′＝ ° ．
3600
例1
计算:⑴1.45°等于多少分? 等于多少秒?
⑵1800″等于多少分? 等于多少度?
解: ⑴ 60′×1.45
=87′,
即 1.45°=87′=5220″.
⑵( ) ′× 1800=
1

60
30′,
60″×87
=5220″,
( ) ° × 30 =
1

60
0.5°,
即 1800″=30′=0.5°.
A
0.25°等于多少分? 等于多少秒?
解：60′× 0.25 = 15′
60″× 15 = 900″
即0.25°= 15′= 900″.
练一练



B
2700″等于多少分? 等于多少度?
解:
( ) ″×2700=45′

( ) °× 45 =0.75°

即2700″=45′=0.75°.
1

60
1

60



C

1
8

(
) °等于多少分? 等于多少秒?

1
8

解: 60′× =7.5′
60″×7.5 =450″
即( ) °=7.5′=450″.
1
8




6000″等于多少分? 等于多少度?
( ) ′×6000=100′

( ) °× 100 = ( )°

即6000″=45′=( )°.
1

60
解:
1

60
5

3
5

3



例题 1 填空
（1）34.50= 0 /
（2）112.270= 0 / //
解：（1）34.50=340+0.50
=340+0.5×60/
=340+3 0/=34030/
（2）112.270=1120+0.27×60/
=1120+16.2/
=1120+16/+0.2×60//
=112016/12//
34
30
112
16
12
例2．计算下列各题：
(1)153°16′42″＋26°40′28″；
?
?
(2)33°15′16″×5；
?
??
＝(153＋26)°(16＋40)′(42＋28)″＝179°56′70″＝179°57′10″；
＝(33×5)°(15×5)′(16×5)″
＝165°75′80″＝166°16′20″；







(3)175°16′30″－47°30′÷6＋4°12′50″×3.
?
＝175°16′30″－(47÷6)°(30÷6)′＋(4×3)°(12×3)′(50×3)″
＝175°16′30″－7°(330÷6)′＋12°36′150″
＝175°16′30″－7°55′＋12°38′30″
＝(174－7＋12)°(76－55＋38)′(30＋30)″
＝179°59′60″
＝180°.







练习
练习
















确定相应钟表上时针与分针所成的角度
开动脑筋
120°
钟表上有12大格，
每小时时针走1大
格，时针转
30°
钟表上有60小格，
每分钟分针走1小
格，分针转
360°÷60=6°
4：00
3
6
10

3、如下图，A、B、C在一直线上，已知
∠1=53°， ∠2=37°；CD与CE垂直吗？


2


1
A
E
D
B
时钟在8点20分时,时钟的时针与分针所成的角是多少度?


课外拓展
18．从6时到7时，钟表面上的时针与分针何时成60°夹角？
【思路点拨】本题有两种情况：一是分针从6时出发在追上时针前的夹角是60°；二是分针从6时出发，追上并超过时针后的夹角为60°.


作业布置
完成练习册上的作业
https://www.21cnjy.com/help/help_extract.php