湘教版八年级数学上册第5章 二次根式5.3 二次根式的加法和减法教学课件(共33张)
文档属性
| 名称 | 湘教版八年级数学上册第5章 二次根式5.3 二次根式的加法和减法教学课件(共33张) |  | |
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 22:46:12 | ||
图片预览











文档简介
(共33张PPT)
二次根式的加法和减法
教学课件
湘教版八年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
计算:
(1)2x - 5x (2)
解:(1)原式=-3 x (2)原式=
上述运算实际上就是合并同类项,如果把题中x换成 ,把换成 ,我们又该如何计算呢?是不是和以前一样呢?让我们一起探究二次根式的加减法则吧!
02 新知探究
新知探究
可以合并的二次根式的加减运算
将二次根式化成最简式,如果被开方数相同,则这样的二次根式可以合并.
新课导入中我们不难发现,所有可以合并的加减运算其对应的元素是一致的,那么对于二次根式,会有什么相类似的情况吗?
注意:判断几个二次根式是否可以合并,一定都要化为最简二次根式再判断.
合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:
新知探究
练一练
1.若最简根式 与 可以合并,求 的值.
解:由题意得 解得
即
确定可以合并的二次根式中字母取值的方法:利用被开方数相同,指数都为2,列关于待定字母的方程求解即可.
归纳
新知探究
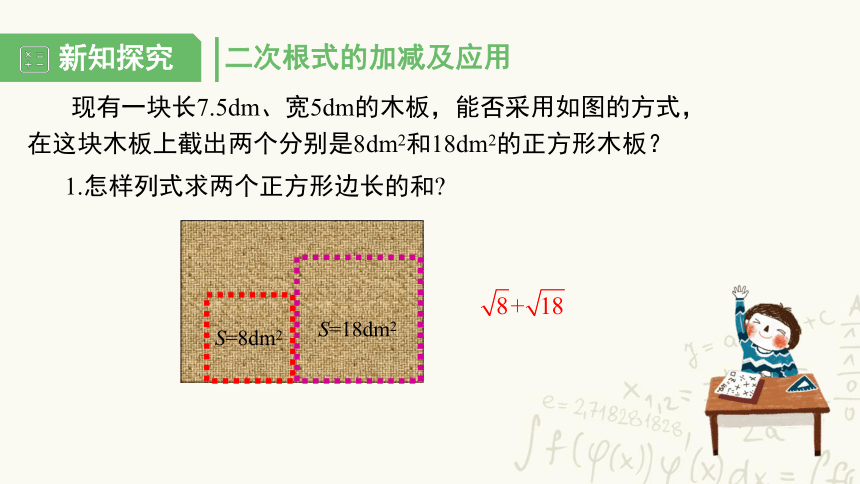
二次根式的加减及应用
现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个分别是8dm2和18dm2的正方形木板?
1.怎样列式求两个正方形边长的和?
S=18dm2
S=8dm2
新知探究
二次根式的加减及应用
2. 所列算式能直接进行加减运算吗?如果不能,把式中各个二次根式化成最简二次根式后,再试一试(说出每步运算的依据).
解:列式如下:
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
在有理数范围内成立的运算律,在实数范围内仍然成立.
新知探究
小归纳
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
加减法的运算步骤:
(1)化——将非最简二次根式的二次根式化简;
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
新知探究
练一练
3. 计算:
解:
新知探究
二次根式的混合运算
烟台、青岛两个城市间计划修建一条城际铁路, 其中有一段路基的横断面设计为上底宽 ,下底宽 ,高 的梯形,这段路基长 500 m,那么这段路基的土石方 (路基的土石方即等于路基的体积)为多少立方米呢?
新知探究
二次根式的混合运算
解:路基的土石方等于路基横断面面积乘以路基的长度,所
以,这段路基的土石方为:
从上面的解答过程可以看到,二次根式的混合运算是根据实数的运算律进行的.
新知探究
练一练
4. 计算:
新知探究
小归纳
二次根式的混合运算,一般先将二次根式转化为最简二次根式,再灵活运用乘法公式等知识来简化计算.
新知探究
二次根式的应用
5.已知 试求x2+2xy+y2的值.
解: x2+2xy+y2=(x+y)2
把 代入上式得
原式=
新知探究
练一练
6. 已知 ,求x3y+xy3.
解:∵
∴
∴
用整体代入法求代数式值的方法:求关于x,y的对称式(即交换任意两个字母的位置后,代数式不变)的值,一般先求 x+y, xy, x-y, 等的值,然后将所求代数式适当变形成知含 x+y, xy, x-y, 等式子,再代入求值.
归纳
新知探究
练一练
7. 计算:
解:
分母形如 的式子,分子、分母同乘以
的式子,构成平方差公式,可以使分母不含根号.
归纳
03 典型例题
例题讲解
1.二次根式: 中,与 能进行合并的
是 ( )
A.
B .
C .
D .
C
2.下列运算中错误的是 ( )
A.
B.
C.
D.
A
例题讲解
3.三角形的三边长分别为 则这个三角形的周长为__________.
4.计算:
例题讲解
5.已知 的整数部分是a,小数部分是b,求a2-b2的值.
解:
例题讲解
6. 教师节就要到了,李欣同学准备做两张大小不同的正方形贺卡送给老师以表示祝贺,其中一张面积为288平方厘米,另一张面积为338平方厘米.如果用彩带把贺卡镶边会更漂亮,她现在有1.5米的彩带,请你帮忙算一算她的彩带够不够用.
分析:可以通过两个正方形的面积分别计算出正方形的边长,进一步求出两个正方形的周长之和,与1.5米比较即可得出结论.
例题讲解
解:贺卡的周长为
答:李欣的彩带够用.
总结:本题是利用二次根式的加法来解决实际生活中的问题,解答本题的关键在于理解题意并列出算式.
04 拓展提高
拓展提高
1. 已知a,b都是有理数,现定义新运算:a*b=
求(2*3)-(27*32)的值.
解:∵a*b= ,
∴(2*3)-(27*32)
=
=
=
拓展提高
2.阅读下列材料,然后回答问题:
在进行类似于二次根式 的运算时,通常有如下两种方法将其进一步化简:
方法一:
方法二:
拓展提高
(1)请用两种不同的方法化简:
(2)化简:
解:(1)?
?
05 课堂小结
课堂小结
二次根式加减
法则
注意
一般地,二次根式的加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
运算原理
运算顺序
运算律仍然适用
与实数的运算顺序一样
06 作业布置
1、完成课本习题 5.3 A、B组
2、复习本章所学,完成复习题5
作业布置
谢 谢 观 看
二次根式的加法和减法
教学课件
湘教版八年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
计算:
(1)2x - 5x (2)
解:(1)原式=-3 x (2)原式=
上述运算实际上就是合并同类项,如果把题中x换成 ,把换成 ,我们又该如何计算呢?是不是和以前一样呢?让我们一起探究二次根式的加减法则吧!
02 新知探究
新知探究
可以合并的二次根式的加减运算
将二次根式化成最简式,如果被开方数相同,则这样的二次根式可以合并.
新课导入中我们不难发现,所有可以合并的加减运算其对应的元素是一致的,那么对于二次根式,会有什么相类似的情况吗?
注意:判断几个二次根式是否可以合并,一定都要化为最简二次根式再判断.
合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:
新知探究
练一练
1.若最简根式 与 可以合并,求 的值.
解:由题意得 解得
即
确定可以合并的二次根式中字母取值的方法:利用被开方数相同,指数都为2,列关于待定字母的方程求解即可.
归纳
新知探究
二次根式的加减及应用
现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个分别是8dm2和18dm2的正方形木板?
1.怎样列式求两个正方形边长的和?
S=18dm2
S=8dm2
新知探究
二次根式的加减及应用
2. 所列算式能直接进行加减运算吗?如果不能,把式中各个二次根式化成最简二次根式后,再试一试(说出每步运算的依据).
解:列式如下:
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
在有理数范围内成立的运算律,在实数范围内仍然成立.
新知探究
小归纳
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
加减法的运算步骤:
(1)化——将非最简二次根式的二次根式化简;
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
新知探究
练一练
3. 计算:
解:
新知探究
二次根式的混合运算
烟台、青岛两个城市间计划修建一条城际铁路, 其中有一段路基的横断面设计为上底宽 ,下底宽 ,高 的梯形,这段路基长 500 m,那么这段路基的土石方 (路基的土石方即等于路基的体积)为多少立方米呢?
新知探究
二次根式的混合运算
解:路基的土石方等于路基横断面面积乘以路基的长度,所
以,这段路基的土石方为:
从上面的解答过程可以看到,二次根式的混合运算是根据实数的运算律进行的.
新知探究
练一练
4. 计算:
新知探究
小归纳
二次根式的混合运算,一般先将二次根式转化为最简二次根式,再灵活运用乘法公式等知识来简化计算.
新知探究
二次根式的应用
5.已知 试求x2+2xy+y2的值.
解: x2+2xy+y2=(x+y)2
把 代入上式得
原式=
新知探究
练一练
6. 已知 ,求x3y+xy3.
解:∵
∴
∴
用整体代入法求代数式值的方法:求关于x,y的对称式(即交换任意两个字母的位置后,代数式不变)的值,一般先求 x+y, xy, x-y, 等的值,然后将所求代数式适当变形成知含 x+y, xy, x-y, 等式子,再代入求值.
归纳
新知探究
练一练
7. 计算:
解:
分母形如 的式子,分子、分母同乘以
的式子,构成平方差公式,可以使分母不含根号.
归纳
03 典型例题
例题讲解
1.二次根式: 中,与 能进行合并的
是 ( )
A.
B .
C .
D .
C
2.下列运算中错误的是 ( )
A.
B.
C.
D.
A
例题讲解
3.三角形的三边长分别为 则这个三角形的周长为__________.
4.计算:
例题讲解
5.已知 的整数部分是a,小数部分是b,求a2-b2的值.
解:
例题讲解
6. 教师节就要到了,李欣同学准备做两张大小不同的正方形贺卡送给老师以表示祝贺,其中一张面积为288平方厘米,另一张面积为338平方厘米.如果用彩带把贺卡镶边会更漂亮,她现在有1.5米的彩带,请你帮忙算一算她的彩带够不够用.
分析:可以通过两个正方形的面积分别计算出正方形的边长,进一步求出两个正方形的周长之和,与1.5米比较即可得出结论.
例题讲解
解:贺卡的周长为
答:李欣的彩带够用.
总结:本题是利用二次根式的加法来解决实际生活中的问题,解答本题的关键在于理解题意并列出算式.
04 拓展提高
拓展提高
1. 已知a,b都是有理数,现定义新运算:a*b=
求(2*3)-(27*32)的值.
解:∵a*b= ,
∴(2*3)-(27*32)
=
=
=
拓展提高
2.阅读下列材料,然后回答问题:
在进行类似于二次根式 的运算时,通常有如下两种方法将其进一步化简:
方法一:
方法二:
拓展提高
(1)请用两种不同的方法化简:
(2)化简:
解:(1)?
?
05 课堂小结
课堂小结
二次根式加减
法则
注意
一般地,二次根式的加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
运算原理
运算顺序
运算律仍然适用
与实数的运算顺序一样
06 作业布置
1、完成课本习题 5.3 A、B组
2、复习本章所学,完成复习题5
作业布置
谢 谢 观 看
同课章节目录
