1.2.1 任意角的三角函数(二)学案
文档属性
| 名称 | 1.2.1 任意角的三角函数(二)学案 |  | |
| 格式 | zip | ||
| 文件大小 | 493.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-16 10:58:09 | ||
图片预览




文档简介
1.2.1 任意角的三角函数(二)
内容要求 1.掌握正弦、余弦、正切函数的定义域(重点).2.了解三角函数线的意义,能用三角函数线表示一个角的正弦、余弦和正切(重点).3.能利用三角函数线解决一些简单的三角函数问题(难点).
知识点1 三角函数的定义域
正弦函数y=sin x的定义域是R;余弦函数y=cos x的定义域是R;正切函数y=tan x的定义域是{x|x∈R且x≠kπ+,k∈Z}.
【预习评价】
函数y=的定义域为________.
解析 由cos x≥0得{x|2kπ-≤x≤2kπ+,k∈Z}.
答案 {x|2kπ-≤x≤2kπ+,k∈Z}
知识点2 三角函数线
1.相关概念
(1)单位圆:
以原点O为圆心,以单位长度为半径的圆.
(2)有向线段:
带有方向(规定了起点和终点)的线段.
规定:方向与x轴或y轴的正方向一致的为正值,反之为负值.
2.三角函数线
题型一 三角函数线及其作法
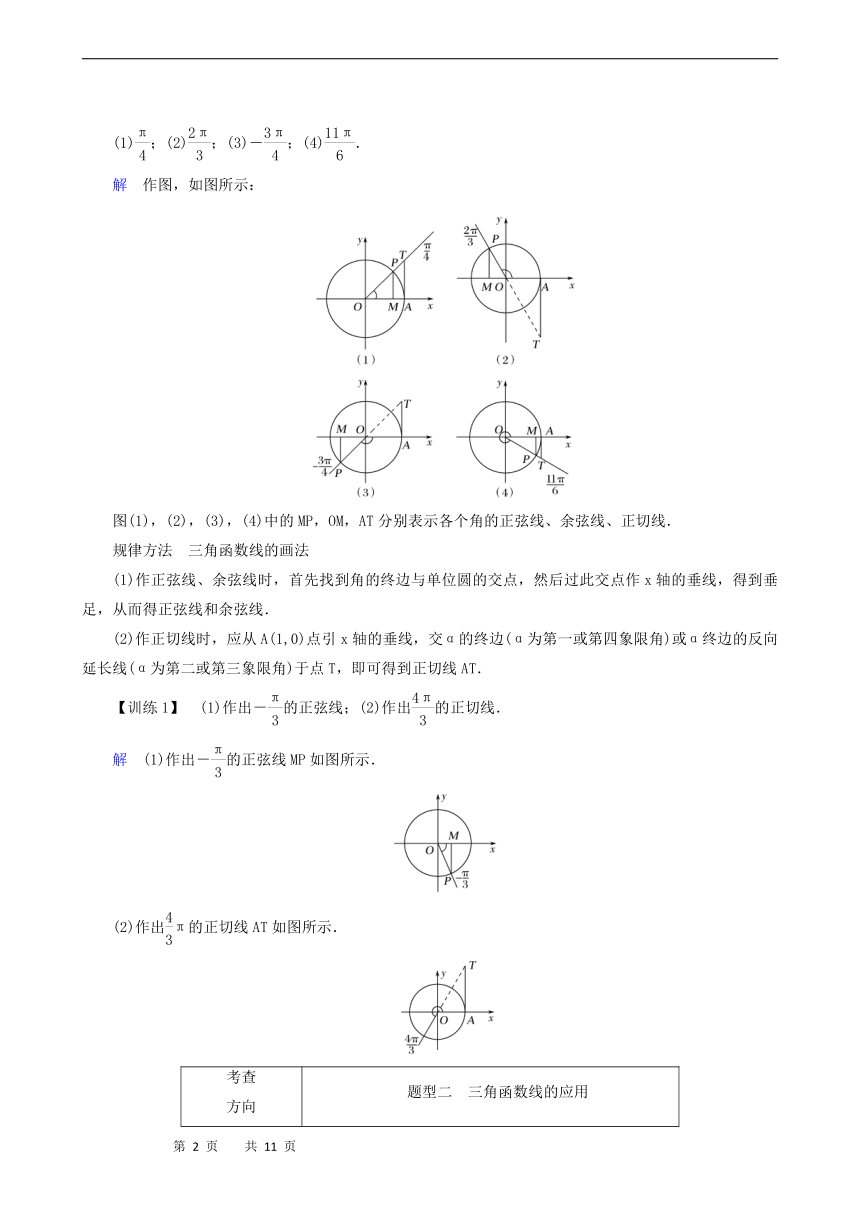
【例1】 分别作出下列各角的正弦线、余弦线、正切线.
(1);(2);(3)-;(4).
解 作图,如图所示:
图(1),(2),(3),(4)中的MP,OM,AT分别表示各个角的正弦线、余弦线、正切线.
规律方法 三角函数线的画法
(1)作正弦线、余弦线时,首先找到角的终边与单位圆的交点,然后过此交点作x轴的垂线,得到垂足,从而得正弦线和余弦线.
(2)作正切线时,应从A(1,0)点引x轴的垂线,交α的终边(α为第一或第四象限角)或α终边的反向延长线(α为第二或第三象限角)于点T,即可得到正切线AT.
【训练1】 (1)作出-的正弦线;(2)作出的正切线.
解 (1)作出-的正弦线MP如图所示.
(2)作出π的正切线AT如图所示.
考查
方向
题型二 三角函数线的应用
方向1 利用三角函数线比较大小
【例2-1】 利用三角函数线比较下列各组数的大小:
(1)sin与sin;(2)tan与tan.
解 如图所示,角的终边与单位圆的交点为P,其反向延长线与单位圆的过点A的切线的交点为T,作PM⊥x轴,垂足为M,sin=MP,tan=AT;
的终边与单位圆的交点为P′,其反向延长线与单位圆的过点A的切线的交点为T′,作P′M′⊥x轴,垂足为M′,则sin=M′P′,tan=AT′,
由图可见,MP>M′P′>0,AT所以(1)sin>sin,(2)tan方向2 利用三角函数线解不等式
【例2-2】 在单位圆中画出适合下列条件的角α的终边的范围,并由此写出角α的集合:
(1)sin α≥;(2)tan α≥-1.
解 (1)作直线y=交单位圆于A,B两点,连接OA,OB,则OA与OB围成的区域即为角α的终边的范围,如图所示,故满足条件的角α的集合为
.
(2)在单位圆过点A(1,0)的切线上取AT=-1,连接OT,OT所在直线与单位圆交于P1,P2两点,则图中阴影部分即为角α终边的范围,如图所示,所以α的取值集合是.
规律方法 1.利用三角函数线比较大小的两个注意点
(1)角的终边的位置要找准;
(2)比较两个三角函数值的大小,不仅要看其长度,还要看其方向.
2.利用三角函数线解不等式的方法
(1)首先作出单位圆,然后根据各问题的约束条件,利用三角函数线画出角α满足条件的终边范围.
(2)角的终边与单位圆交点的横坐标是该角的余弦值,与单位圆交点的纵坐标是该角的正弦值.
(3)写角的范围时,抓住边界值,然后再注意角的范围的写法要求.
【训练2】 解不等式cos α≤-.
解 作直线x=-交单位圆于C,D两点,连接OC,OD,则OC与OD围成的区域(图中阴影部分)即为角α终边的范围,如图所示,故满足条件的角α的集合为.
题型三 求三角函数的定义域
【例3】 求下列函数的定义域:
(1)f(x)=;
(2)f(x)=lg sin x+.
解 (1)∵要使函数f(x)有意义,
∴sin x·tan x≥0,
∴sin x与tan x同号或sin x·tan x=0,
故x是第一、四象限的角或终边在x轴上的角.
∴函数的定义域为{x|2kπ-x=(2k+1)π,k∈Z}.
(2)由题意,要使f(x)有意义,则
由sin x>0得2kπ由9-x2≥0得-3≤x≤3, ②
由①②得:f(x)的定义域为{x|0<x≤3}.
规律方法 求三角函数定义域的方法
(1)求函数的定义域,就是求使解析式有意义的自变量的取值范围,一般通过解不等式或不等式组求得,对于三角函数的定义域问题,还要考虑三角函数自身定义域的限制.
(2)要特别注意求一个固定集合与一个含有无限多段的集合的交集时,可以用取特殊值把不固定的集合写成若干个固定集合再求交集.
【训练3】 求下列函数的定义域:
(1)y=;(2)y=lg(3-4sin2x).
解 (1)∵2cos x-1≥0,∴cos x≥.
如图,
∴x∈(k∈Z).
∴函数的定义域为
.
(2)∵3-4sin2x>0,∴sin2x<,
∴-∴x∈∪(k∈Z).
即x∈(k∈Z).
∴函数的定义域为(k∈Z).
课堂达标
1.下列四个命题中:
①α一定时 ,单位圆中的正弦线一定;
②单位圆中,有相同正弦线的角相等;
③α和α+π有相同的正切线;
④具有相同正切线的两个角终边在同一条直线上.
不正确命题的个数是( )
A.0 B.1
C.2 D.3
解析 由三角函数线的定义①③④正确,②不正确.
答案 B
2.如果<α<,那么下列不等式成立的是( )
A.cos αC.sin α解析 方法一 (特值法)令α=,则cos α=,tan α=,sin α=,故cos αtan α.
方法二 如图所示,在单位圆中分别作出α的正弦线MP、余弦线OM、正切线AT,则OM答案 A
3.比较大小:sin 1________sin(填“>”或“<”).
解析 因为0<1<<,结合单位圆中的三角函数线,知sin 1答案 <
4.当x∈[0,2π]时,不等式sin x≥的解集为________.
解析 如图所示,不等式的解集为{x|≤x≤}.
答案
5.比较sin与tan的大小.
解 的正弦线MP与正切线AT如图所示.
由图易知sin>0,tan<0,∴sin>tan.
基础过关
1.下列说法不正确的是( )
A.当角α的终边在x轴上时,角α的正切线是一个点
B.当角α的终边在y轴上时,角α的正切线不存在
C.正弦线的始点随角的终边位置的变化而变化
D.余弦线和正切线的始点都是原点
解析 根据三角函数线的概念,A,B,C是正确的,只有D不正确,因为余弦线的始点在原点而正切线的始点在单位圆与x轴正半轴的交点上.
答案 D
2.使sin x≤cos x成立的x的一个变化区间是( )
A. B.
C. D.[0,π]
解析 如图所示,当x=和x=-时,sin x=cos x,故使sin x≤cos x成立的x的一个变化区间是[-,].
答案 A
3.函数f(x)=tan(2x-)的定义域为( )
A.{x|x≠+kπ,k∈Z} B.{x|x≠+kπ,k∈Z}
C.{x|x≠+2kπ,k∈Z} D.{x|x≠+kπ,k∈Z}
解析 易知2x-≠+kπ,,k∈Z,即x≠+kπ,k∈Z,故f(x)的定义域为{x|x≠+kπ,k∈Z}.
答案 A
4.若θ∈(,),则sin θ的取值范围是________.
解析 如图所示,作出和的正弦线,
可得sin θ∈(-,1).
答案 (-,1)
5.比较大小:sin 1.2________sin 1.5(填“>”或“<”).
解析 ∵1.2∈(0,),1.5∈(0,),正弦线在(0,)内随角α的增大而增大,
∴sin 1.2答案 <
6.在单位圆中画出适合下列条件的角α的终边.
(1)sin α=;(2)cos α=-.
解 (1)作直线y=交单位圆于P,Q两点,则OP,OQ为角α的终边,如图甲.
(2)作直线x=-交单位圆于M,N两点,则OM,ON为角α的终边,如图乙.
7.求函数f(x)=+ln的定义域.
解 由题意,得自变量x应满足不等式组
即
则不等式组的解的集合如图(阴影部分)所示,
即定义域为.
能力提升
8.点P(sin 3-cos 3,sin 3+cos 3)所在的象限为( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析 ∵π<3<π,作出单位圆如图所示.
设MP,OM分别为a,b.
sin 3=a>0,cos 3=b<0,
所以sin 3-cos 3>0.
因为|MP|<|OM|即|a|<|b|,
所以sin 3+cos 3=a+b<0.
故点P(sin 3-cos 3,sin 3+cos 3)在第四象限.
答案 D
9.已知函数f(x)=2asin+b的定义域为,值域为[-5,1],则函数g(x)=
abx+7在[b,a]上( )
A.有最大值2 B.有最小值2
C.有最大值1 D.有最小值1
解析 易知2x+∈[,],a>0,∴由三角函数线易得f(x)∈[-a+b,2a+b],即解得
∴g(x)=2-3x+7,x∈[-3,2],故当x=2时,g(x)有最小值2.
答案 B
10.函数f(x)=的定义域为________.
解析 如图所示.
答案 { x |kπ-≤ x≤ kπ+(k∈Z)]
11.sin 1,cos 1,tan 1的大小关系是________.
解析 由题意1>,在单位圆中作出锐角α=1的正切线、正弦线、余弦线,可知正切线最长,余弦线最短,所以有cos 1答案 cos 112.设θ是第二象限角,试比较sin ,cos ,tan 的大小.
解
θ是第二象限角,
即2kπ+<θ<2kπ+π(k∈Z),
故kπ+<作出所在范围如图所示.
当2kπ+<<2kπ+(k∈Z)时,
cos当2kπ+<<2kπ+π(k∈Z)时,
sin13.(选做题)利用三角函数线证明:若0<α<β<,则β-α>sin β-sin α.
证明 如图,单位圆O与x轴正半轴交于点A,与角α,β的终边分别交于点Q,P,过P,Q分别作OA的垂线,设垂足分别为点M,N,则由三角函数线定义可知:
sin α=NQ,sin β=MP,过点Q作QH⊥MP于点H,于是MH=NQ,则HP=MP-MH=sin β-sin α.
由图可知HP<=-=β-α,
即β-α>sin β-sin α.
内容要求 1.掌握正弦、余弦、正切函数的定义域(重点).2.了解三角函数线的意义,能用三角函数线表示一个角的正弦、余弦和正切(重点).3.能利用三角函数线解决一些简单的三角函数问题(难点).
知识点1 三角函数的定义域
正弦函数y=sin x的定义域是R;余弦函数y=cos x的定义域是R;正切函数y=tan x的定义域是{x|x∈R且x≠kπ+,k∈Z}.
【预习评价】
函数y=的定义域为________.
解析 由cos x≥0得{x|2kπ-≤x≤2kπ+,k∈Z}.
答案 {x|2kπ-≤x≤2kπ+,k∈Z}
知识点2 三角函数线
1.相关概念
(1)单位圆:
以原点O为圆心,以单位长度为半径的圆.
(2)有向线段:
带有方向(规定了起点和终点)的线段.
规定:方向与x轴或y轴的正方向一致的为正值,反之为负值.
2.三角函数线
题型一 三角函数线及其作法
【例1】 分别作出下列各角的正弦线、余弦线、正切线.
(1);(2);(3)-;(4).
解 作图,如图所示:
图(1),(2),(3),(4)中的MP,OM,AT分别表示各个角的正弦线、余弦线、正切线.
规律方法 三角函数线的画法
(1)作正弦线、余弦线时,首先找到角的终边与单位圆的交点,然后过此交点作x轴的垂线,得到垂足,从而得正弦线和余弦线.
(2)作正切线时,应从A(1,0)点引x轴的垂线,交α的终边(α为第一或第四象限角)或α终边的反向延长线(α为第二或第三象限角)于点T,即可得到正切线AT.
【训练1】 (1)作出-的正弦线;(2)作出的正切线.
解 (1)作出-的正弦线MP如图所示.
(2)作出π的正切线AT如图所示.
考查
方向
题型二 三角函数线的应用
方向1 利用三角函数线比较大小
【例2-1】 利用三角函数线比较下列各组数的大小:
(1)sin与sin;(2)tan与tan.
解 如图所示,角的终边与单位圆的交点为P,其反向延长线与单位圆的过点A的切线的交点为T,作PM⊥x轴,垂足为M,sin=MP,tan=AT;
的终边与单位圆的交点为P′,其反向延长线与单位圆的过点A的切线的交点为T′,作P′M′⊥x轴,垂足为M′,则sin=M′P′,tan=AT′,
由图可见,MP>M′P′>0,AT
【例2-2】 在单位圆中画出适合下列条件的角α的终边的范围,并由此写出角α的集合:
(1)sin α≥;(2)tan α≥-1.
解 (1)作直线y=交单位圆于A,B两点,连接OA,OB,则OA与OB围成的区域即为角α的终边的范围,如图所示,故满足条件的角α的集合为
.
(2)在单位圆过点A(1,0)的切线上取AT=-1,连接OT,OT所在直线与单位圆交于P1,P2两点,则图中阴影部分即为角α终边的范围,如图所示,所以α的取值集合是.
规律方法 1.利用三角函数线比较大小的两个注意点
(1)角的终边的位置要找准;
(2)比较两个三角函数值的大小,不仅要看其长度,还要看其方向.
2.利用三角函数线解不等式的方法
(1)首先作出单位圆,然后根据各问题的约束条件,利用三角函数线画出角α满足条件的终边范围.
(2)角的终边与单位圆交点的横坐标是该角的余弦值,与单位圆交点的纵坐标是该角的正弦值.
(3)写角的范围时,抓住边界值,然后再注意角的范围的写法要求.
【训练2】 解不等式cos α≤-.
解 作直线x=-交单位圆于C,D两点,连接OC,OD,则OC与OD围成的区域(图中阴影部分)即为角α终边的范围,如图所示,故满足条件的角α的集合为.
题型三 求三角函数的定义域
【例3】 求下列函数的定义域:
(1)f(x)=;
(2)f(x)=lg sin x+.
解 (1)∵要使函数f(x)有意义,
∴sin x·tan x≥0,
∴sin x与tan x同号或sin x·tan x=0,
故x是第一、四象限的角或终边在x轴上的角.
∴函数的定义域为{x|2kπ-
(2)由题意,要使f(x)有意义,则
由sin x>0得2kπ
由①②得:f(x)的定义域为{x|0<x≤3}.
规律方法 求三角函数定义域的方法
(1)求函数的定义域,就是求使解析式有意义的自变量的取值范围,一般通过解不等式或不等式组求得,对于三角函数的定义域问题,还要考虑三角函数自身定义域的限制.
(2)要特别注意求一个固定集合与一个含有无限多段的集合的交集时,可以用取特殊值把不固定的集合写成若干个固定集合再求交集.
【训练3】 求下列函数的定义域:
(1)y=;(2)y=lg(3-4sin2x).
解 (1)∵2cos x-1≥0,∴cos x≥.
如图,
∴x∈(k∈Z).
∴函数的定义域为
.
(2)∵3-4sin2x>0,∴sin2x<,
∴-
即x∈(k∈Z).
∴函数的定义域为(k∈Z).
课堂达标
1.下列四个命题中:
①α一定时 ,单位圆中的正弦线一定;
②单位圆中,有相同正弦线的角相等;
③α和α+π有相同的正切线;
④具有相同正切线的两个角终边在同一条直线上.
不正确命题的个数是( )
A.0 B.1
C.2 D.3
解析 由三角函数线的定义①③④正确,②不正确.
答案 B
2.如果<α<,那么下列不等式成立的是( )
A.cos α
方法二 如图所示,在单位圆中分别作出α的正弦线MP、余弦线OM、正切线AT,则OM
3.比较大小:sin 1________sin(填“>”或“<”).
解析 因为0<1<<,结合单位圆中的三角函数线,知sin 1
4.当x∈[0,2π]时,不等式sin x≥的解集为________.
解析 如图所示,不等式的解集为{x|≤x≤}.
答案
5.比较sin与tan的大小.
解 的正弦线MP与正切线AT如图所示.
由图易知sin>0,tan<0,∴sin>tan.
基础过关
1.下列说法不正确的是( )
A.当角α的终边在x轴上时,角α的正切线是一个点
B.当角α的终边在y轴上时,角α的正切线不存在
C.正弦线的始点随角的终边位置的变化而变化
D.余弦线和正切线的始点都是原点
解析 根据三角函数线的概念,A,B,C是正确的,只有D不正确,因为余弦线的始点在原点而正切线的始点在单位圆与x轴正半轴的交点上.
答案 D
2.使sin x≤cos x成立的x的一个变化区间是( )
A. B.
C. D.[0,π]
解析 如图所示,当x=和x=-时,sin x=cos x,故使sin x≤cos x成立的x的一个变化区间是[-,].
答案 A
3.函数f(x)=tan(2x-)的定义域为( )
A.{x|x≠+kπ,k∈Z} B.{x|x≠+kπ,k∈Z}
C.{x|x≠+2kπ,k∈Z} D.{x|x≠+kπ,k∈Z}
解析 易知2x-≠+kπ,,k∈Z,即x≠+kπ,k∈Z,故f(x)的定义域为{x|x≠+kπ,k∈Z}.
答案 A
4.若θ∈(,),则sin θ的取值范围是________.
解析 如图所示,作出和的正弦线,
可得sin θ∈(-,1).
答案 (-,1)
5.比较大小:sin 1.2________sin 1.5(填“>”或“<”).
解析 ∵1.2∈(0,),1.5∈(0,),正弦线在(0,)内随角α的增大而增大,
∴sin 1.2
6.在单位圆中画出适合下列条件的角α的终边.
(1)sin α=;(2)cos α=-.
解 (1)作直线y=交单位圆于P,Q两点,则OP,OQ为角α的终边,如图甲.
(2)作直线x=-交单位圆于M,N两点,则OM,ON为角α的终边,如图乙.
7.求函数f(x)=+ln的定义域.
解 由题意,得自变量x应满足不等式组
即
则不等式组的解的集合如图(阴影部分)所示,
即定义域为.
能力提升
8.点P(sin 3-cos 3,sin 3+cos 3)所在的象限为( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析 ∵π<3<π,作出单位圆如图所示.
设MP,OM分别为a,b.
sin 3=a>0,cos 3=b<0,
所以sin 3-cos 3>0.
因为|MP|<|OM|即|a|<|b|,
所以sin 3+cos 3=a+b<0.
故点P(sin 3-cos 3,sin 3+cos 3)在第四象限.
答案 D
9.已知函数f(x)=2asin+b的定义域为,值域为[-5,1],则函数g(x)=
abx+7在[b,a]上( )
A.有最大值2 B.有最小值2
C.有最大值1 D.有最小值1
解析 易知2x+∈[,],a>0,∴由三角函数线易得f(x)∈[-a+b,2a+b],即解得
∴g(x)=2-3x+7,x∈[-3,2],故当x=2时,g(x)有最小值2.
答案 B
10.函数f(x)=的定义域为________.
解析 如图所示.
答案 { x |kπ-≤ x≤ kπ+(k∈Z)]
11.sin 1,cos 1,tan 1的大小关系是________.
解析 由题意1>,在单位圆中作出锐角α=1的正切线、正弦线、余弦线,可知正切线最长,余弦线最短,所以有cos 1
解
θ是第二象限角,
即2kπ+<θ<2kπ+π(k∈Z),
故kπ+<
当2kπ+<<2kπ+(k∈Z)时,
cos
sin
证明 如图,单位圆O与x轴正半轴交于点A,与角α,β的终边分别交于点Q,P,过P,Q分别作OA的垂线,设垂足分别为点M,N,则由三角函数线定义可知:
sin α=NQ,sin β=MP,过点Q作QH⊥MP于点H,于是MH=NQ,则HP=MP-MH=sin β-sin α.
由图可知HP<=-=β-α,
即β-α>sin β-sin α.
