1.3 三角函数的诱导公式(一)学案
文档属性
| 名称 | 1.3 三角函数的诱导公式(一)学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 172.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-16 00:00:00 | ||
图片预览





文档简介
§1.3 三角函数的诱导公式(一)
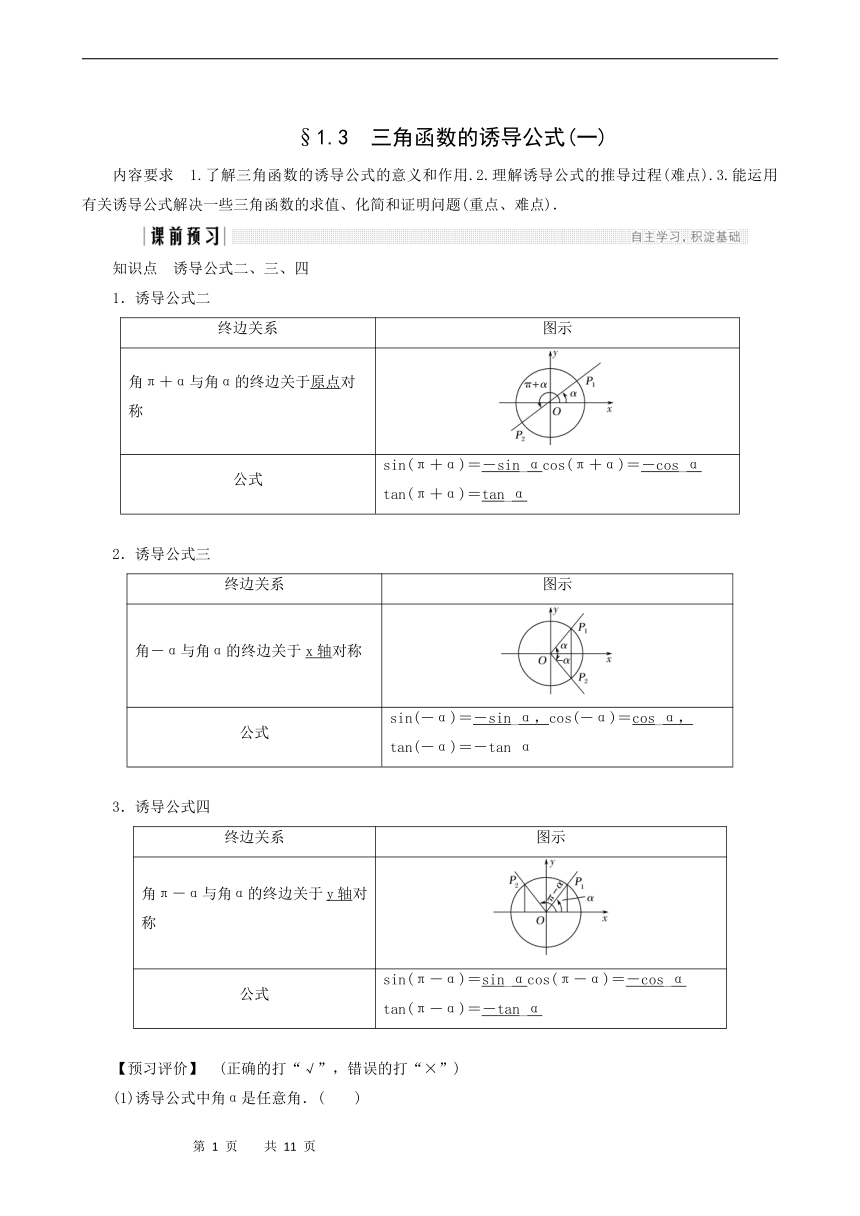
内容要求 1.了解三角函数的诱导公式的意义和作用.2.理解诱导公式的推导过程(难点).3.能运用有关诱导公式解决一些三角函数的求值、化简和证明问题(重点、难点).
知识点 诱导公式二、三、四
1.诱导公式二
终边关系
图示
角π+α与角α的终边关于原点对称
公式
sin(π+α)=-sin_αcos(π+α)=-cos_α
tan(π+α)=tan_α
2.诱导公式三
终边关系
图示
角-α与角α的终边关于x轴对称
公式
sin(-α)=-sin_α,cos(-α)=cos_α,
tan(-α)=-tan α
3.诱导公式四
终边关系
图示
角π-α与角α的终边关于y轴对称
公式
sin(π-α)=sin_αcos(π-α)=-cos_α
tan(π-α)=-tan_α
【预习评价】 (正确的打“√”,错误的打“×”)
(1)诱导公式中角α是任意角.( )
(2)sin(α-π)=sin α.( )
(3)cosπ=-.( )
提示 (1)×,正、余弦函数的诱导公式中,α为任意角,但是正切函数的诱导公式中,α的取值必须使公式中角的正切值有意义.
(2)×,sin(α-π)=sin[-(π-α)]=-sin(π-α)=-sin α.
(3)√,cos=cos(π+)=-cos=-.
题型一 给角求值问题
【例1】 (1)sin 750°=________;cos(-2 040°)=________.;
解析 sin 750°=sin(2×360°+30°)=sin 30°=;
cos(-2 040°)=cos 2 040°=cos(5×360°+240°)=cos 240°
=cos(180°+60°)=-cos 60°=-.
答案 -
(2)计算:sin(-)-cos(-)=________.
解析 原式=-sin-cos=-sin(4π+π+)-cos(2π+π+)=sin+cos=+=1.
答案 1
规律方法 利用诱导公式求任意角三角函数值的步骤
(1)“负化正”:用公式一或三来转化.
(2)“大化小”:用公式一将角化为0°到360°间的角.
(3)“小化锐”:用公式二或四将大于90°的角转化为锐角.
(4)“锐求值”:得到锐角的三角函数后求值.
【训练1】 求下列各三角函数式的值:
(1)sin 1 320°;(2)cos;(3)tan(-945°).
解 (1)方法一 sin 1 320°=sin(3×360°+240°)
=sin 240°=sin(180°+60°)=-sin 60°=-.
方法二 sin 1 320°=sin(4×360°-120°)=sin(-120°)
=-sin(180°-60°)=-sin 60°=-.
(2)方法一 cos=cos=cos
=cos(π+)=-cos=-.
方法二 cos=cos
=cos=-cos=-.
(3)tan(-945°)=-tan 945°=-tan(225°+2×360°)
=-tan 225°=-tan(180°+45°)=-tan 45°=-1.
题型二 化简求值问题
【例2】 (1)计算:cos+cos+cos+cos+cos+cos=________;
解析 原式=cos+cos+cos+cos(π-)+cos(π-)+cos(π-)=cos+cos+cos-cos-cos-cos=0.
答案 0
(2)化简:.
解 原式==·=1.
规律方法 三角函数式化简的常用方法
(1)合理转化:①将角化成2kπ±α,π±α,k∈Z的形式.
②依据所给式子合理选用诱导公式将所给角的三角函数转化为角α的三角函数.
(2)切化弦:一般需将表达式中的切函数转化为弦函数.
【训练2】 化简下列各式:
(1);
(2).
解 (1)原式=
==-=-tan α.
(2)原式=
==
==-1.
典例
迁移
题型三 给值或式求值问题
【例3】 (1) 在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称 .若sin α=,则sin β=________.
解析 α与β的终边关于y轴对称,则α+β=π+2kπ,k∈Z,∴β=π-α+2kπ,k∈Z.
∴sin β=sin(π-α+2kπ)=sin α=.
答案
(2)已知cos(-α)=,求cos(+α)-sin2(α-)的值.
解 因为cos(+α)=cos[π-(-α)]=-cos(-α)=-,
sin2(α-)=sin2(-α)=1-cos2(-α)=1-()2=,
所以cos(+α)-sin2(α-)=--=-.
【迁移1】 将例3(2)题中的“-”改为“+”,“+”改为“-”,其他不变,应如何解答?
解 由题意知cos(+α)=,求cos(-α)+sin2(α+)的值.
因为cos(-α)=cos[π-(+α)]=-cos(+α)=-,
sin2(α+)=1-cos2(+α)=1-()2=,
所以,cos(-α)+sin2(α+)=-+=.
【迁移2】 例3(2)题中的条件不变,求cos(-α)-sin2(α-)的值.
解 cos(-α)-sin2(α-)=cos[π+(-α)]-sin2[(α-)-2π]
=-cos(-α)-sin2(-α)=--=-.
规律方法 解决条件求值问题的策略
(1)解决条件求值问题,首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系.
(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
课堂达标
1.tan 300°+sin 450°的值是( )
A.-1+ B.1+
C.-1- D.1-
解析 原式=tan(360°-60°)+sin(360°+90°)
=tan(-60°)+sin 90°=-tan 60°+1=-+1.
答案 D
2.已知sin=m,则cos的值等于( )
A.m B.-m
C. D.-
解析 cos=cos(π-)=-cos=-(-)=.
答案 C
3.已知600°角的终边上有一点P(a,-3),则a的值为________.
解析 tan 600°=tan(360°+240°)=tan(180°+60°)
=tan 60°=-=,
即a=-.
答案 -
4.已知cos(508°-α)=,则cos(212°+α)=________.
解析 cos(212°+α)=cos[2×360°-(508°-α)]
=cos(508°-α)=.
答案
5.化简:.
解 原式=
=
==1.
课堂小结
1.明确各诱导公式的作用
诱导公式
作用
公式一
将角转化为0~2π之间的角求值
公式二
将0~2π内的角转化为0~π之间的角求值
公式三
将负角转化为正角求值
公式四
将角转化为0~之间的角求值
2.诱导公式的记忆
这四组诱导公式的记忆口诀是“函数名不变,符号看象限”.其含义是诱导公式两边的函数名称一致,符号则是将α看成锐角时原角所在象限的三角函数值的符号.α看成锐角,只是公式记忆的方便,实际上α可以是任意角.
基础过关
1.已知sin(π-α)=,则sin(α-2 017π)的值为( )
A. B.
C. D.-
解析 由sin(π-α)=sin α得sin α=,所以sin(α-2 017π)
=sin[(α-π)-2 016π]=sin(α-π)=-sin(π-α)=-sin α=-.
答案 D
2.若sin(-110°)=a,则tan 70°等于( )
A. B.
C. D.
解析 ∵sin(-110°)=-sin 110°=-sin(180°-70°)
=-sin 70°=a,∴sin 70°=-a,
∴cos 70°==,
∴tan 70°==.
答案 B
3.tan(5π+α)=m(m≠±1),则的值为( )
A. B.
C.-1 D.1
解析 ∵tan(5π+α)=tan α=m,
∴原式===.
答案 A
4.若P(-4,3)是角α终边上一点,则的值为________.
解析 由题意知sin α=,原式==-=-=-.
答案 -
5.的值是________________.
解析 原式=
=
=
===-2.
答案 -2
6.化简下列各式:
(1)sin(-π)cos π;
(2)sin(-960°)cos 1 470°-cos(-240°)sin(-210°).
解 (1)sin(-π)cos π
=-sin(6π+)cos(π+)=sin cos =.
(2)sin(-960°)cos 1 470°-cos(-240°)sin(-210°)
=-sin(180°+60°+2×360°)cos(30°+4×360°)
+cos(180°+60°)sin(180°+30°)
=sin 60°cos 30°+cos 60°sin 30°=1.
7.已知tan(π+α)=-,求下列各式的值:
(1);
(2)sin(α-7π)·cos(α+5π).
解 由tan(π+α)=-,
得tan α=-,
(1)原式=
==
==-.
(2)原式=sin(-6π+α-π)·cos(4π+α+π)
=sin(α-π)·cos(α+π)
=-sin α(-cos α)
=sin αcos α=
==-.
能力提升
8.已知n为整数,化简所得的结果是( )
A.tan(nα) B.-tan(nα)
C.tan α D.-tan α
解析 当n为偶数时,原式==tan α;
当n为奇数时,原式==tan α.故选C.
答案 C
9.设f(x)=asin(πx+α)+bcos(πx+β)+4,其中a,b,α,β∈R,且ab≠0,α≠kπ(k∈Z).若f(2 009)=5,则f(2 017)等于( )
A.4 B.3
C.-5 D.5
解析 f(2 009)=-(asin α+bcos β)+4=5,
f(2 017)=-(asin α+bcos β)+4=5.
答案 D
10.若cos(π+α)=-,π<α<2π,则sin(α-2π)=________.
解析 由cos(π+α)=-,得cos α=,
故sin(α-2π)=sin α=-=-
=-(α为第四象限角).
答案 -
11.已知a=tan,b=cos,c=sin,则a,b,c的大小关系是________.
解析 a=-tan=-tan=-,
b=cos=cos=,
c=-sin=-sin=-,
∴b>a>c.
答案 b>a>c
12.若cos(α-π)=-,求
的值.
解 原式=
===-tan α.
∵cos(α-π)=cos(π-α)=-cos α=-,
∴cos α=.∴α为第一象限角或第四象限角.
当α为第一象限角时,cos α=,
sin α==,
∴tan α==,
∴原式=-.
当α为第四象限角时,cos α=,
sin α=-=-,
∴tan α==-,∴原式=.
综上,原式=±.
13.(选做题)在△ABC中,若sin(2π-A)=-sin(π-B),cos A=-cos(π-B),求△ABC的三个内角.
解 由条件得sin A=sin B,cos A=cos B,
平方相加得2cos2A=1,cos A=±,
又∵A∈(0,π),
∴A=或π.
当A=π时,cos B=-<0,
∴B∈,
∴A,B均为钝角,不合题意,舍去.
∴A=,cos B=,
∴B=,∴C=π.
综上所述,A=,B=,C=π.
内容要求 1.了解三角函数的诱导公式的意义和作用.2.理解诱导公式的推导过程(难点).3.能运用有关诱导公式解决一些三角函数的求值、化简和证明问题(重点、难点).
知识点 诱导公式二、三、四
1.诱导公式二
终边关系
图示
角π+α与角α的终边关于原点对称
公式
sin(π+α)=-sin_αcos(π+α)=-cos_α
tan(π+α)=tan_α
2.诱导公式三
终边关系
图示
角-α与角α的终边关于x轴对称
公式
sin(-α)=-sin_α,cos(-α)=cos_α,
tan(-α)=-tan α
3.诱导公式四
终边关系
图示
角π-α与角α的终边关于y轴对称
公式
sin(π-α)=sin_αcos(π-α)=-cos_α
tan(π-α)=-tan_α
【预习评价】 (正确的打“√”,错误的打“×”)
(1)诱导公式中角α是任意角.( )
(2)sin(α-π)=sin α.( )
(3)cosπ=-.( )
提示 (1)×,正、余弦函数的诱导公式中,α为任意角,但是正切函数的诱导公式中,α的取值必须使公式中角的正切值有意义.
(2)×,sin(α-π)=sin[-(π-α)]=-sin(π-α)=-sin α.
(3)√,cos=cos(π+)=-cos=-.
题型一 给角求值问题
【例1】 (1)sin 750°=________;cos(-2 040°)=________.;
解析 sin 750°=sin(2×360°+30°)=sin 30°=;
cos(-2 040°)=cos 2 040°=cos(5×360°+240°)=cos 240°
=cos(180°+60°)=-cos 60°=-.
答案 -
(2)计算:sin(-)-cos(-)=________.
解析 原式=-sin-cos=-sin(4π+π+)-cos(2π+π+)=sin+cos=+=1.
答案 1
规律方法 利用诱导公式求任意角三角函数值的步骤
(1)“负化正”:用公式一或三来转化.
(2)“大化小”:用公式一将角化为0°到360°间的角.
(3)“小化锐”:用公式二或四将大于90°的角转化为锐角.
(4)“锐求值”:得到锐角的三角函数后求值.
【训练1】 求下列各三角函数式的值:
(1)sin 1 320°;(2)cos;(3)tan(-945°).
解 (1)方法一 sin 1 320°=sin(3×360°+240°)
=sin 240°=sin(180°+60°)=-sin 60°=-.
方法二 sin 1 320°=sin(4×360°-120°)=sin(-120°)
=-sin(180°-60°)=-sin 60°=-.
(2)方法一 cos=cos=cos
=cos(π+)=-cos=-.
方法二 cos=cos
=cos=-cos=-.
(3)tan(-945°)=-tan 945°=-tan(225°+2×360°)
=-tan 225°=-tan(180°+45°)=-tan 45°=-1.
题型二 化简求值问题
【例2】 (1)计算:cos+cos+cos+cos+cos+cos=________;
解析 原式=cos+cos+cos+cos(π-)+cos(π-)+cos(π-)=cos+cos+cos-cos-cos-cos=0.
答案 0
(2)化简:.
解 原式==·=1.
规律方法 三角函数式化简的常用方法
(1)合理转化:①将角化成2kπ±α,π±α,k∈Z的形式.
②依据所给式子合理选用诱导公式将所给角的三角函数转化为角α的三角函数.
(2)切化弦:一般需将表达式中的切函数转化为弦函数.
【训练2】 化简下列各式:
(1);
(2).
解 (1)原式=
==-=-tan α.
(2)原式=
==
==-1.
典例
迁移
题型三 给值或式求值问题
【例3】 (1) 在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称 .若sin α=,则sin β=________.
解析 α与β的终边关于y轴对称,则α+β=π+2kπ,k∈Z,∴β=π-α+2kπ,k∈Z.
∴sin β=sin(π-α+2kπ)=sin α=.
答案
(2)已知cos(-α)=,求cos(+α)-sin2(α-)的值.
解 因为cos(+α)=cos[π-(-α)]=-cos(-α)=-,
sin2(α-)=sin2(-α)=1-cos2(-α)=1-()2=,
所以cos(+α)-sin2(α-)=--=-.
【迁移1】 将例3(2)题中的“-”改为“+”,“+”改为“-”,其他不变,应如何解答?
解 由题意知cos(+α)=,求cos(-α)+sin2(α+)的值.
因为cos(-α)=cos[π-(+α)]=-cos(+α)=-,
sin2(α+)=1-cos2(+α)=1-()2=,
所以,cos(-α)+sin2(α+)=-+=.
【迁移2】 例3(2)题中的条件不变,求cos(-α)-sin2(α-)的值.
解 cos(-α)-sin2(α-)=cos[π+(-α)]-sin2[(α-)-2π]
=-cos(-α)-sin2(-α)=--=-.
规律方法 解决条件求值问题的策略
(1)解决条件求值问题,首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系.
(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
课堂达标
1.tan 300°+sin 450°的值是( )
A.-1+ B.1+
C.-1- D.1-
解析 原式=tan(360°-60°)+sin(360°+90°)
=tan(-60°)+sin 90°=-tan 60°+1=-+1.
答案 D
2.已知sin=m,则cos的值等于( )
A.m B.-m
C. D.-
解析 cos=cos(π-)=-cos=-(-)=.
答案 C
3.已知600°角的终边上有一点P(a,-3),则a的值为________.
解析 tan 600°=tan(360°+240°)=tan(180°+60°)
=tan 60°=-=,
即a=-.
答案 -
4.已知cos(508°-α)=,则cos(212°+α)=________.
解析 cos(212°+α)=cos[2×360°-(508°-α)]
=cos(508°-α)=.
答案
5.化简:.
解 原式=
=
==1.
课堂小结
1.明确各诱导公式的作用
诱导公式
作用
公式一
将角转化为0~2π之间的角求值
公式二
将0~2π内的角转化为0~π之间的角求值
公式三
将负角转化为正角求值
公式四
将角转化为0~之间的角求值
2.诱导公式的记忆
这四组诱导公式的记忆口诀是“函数名不变,符号看象限”.其含义是诱导公式两边的函数名称一致,符号则是将α看成锐角时原角所在象限的三角函数值的符号.α看成锐角,只是公式记忆的方便,实际上α可以是任意角.
基础过关
1.已知sin(π-α)=,则sin(α-2 017π)的值为( )
A. B.
C. D.-
解析 由sin(π-α)=sin α得sin α=,所以sin(α-2 017π)
=sin[(α-π)-2 016π]=sin(α-π)=-sin(π-α)=-sin α=-.
答案 D
2.若sin(-110°)=a,则tan 70°等于( )
A. B.
C. D.
解析 ∵sin(-110°)=-sin 110°=-sin(180°-70°)
=-sin 70°=a,∴sin 70°=-a,
∴cos 70°==,
∴tan 70°==.
答案 B
3.tan(5π+α)=m(m≠±1),则的值为( )
A. B.
C.-1 D.1
解析 ∵tan(5π+α)=tan α=m,
∴原式===.
答案 A
4.若P(-4,3)是角α终边上一点,则的值为________.
解析 由题意知sin α=,原式==-=-=-.
答案 -
5.的值是________________.
解析 原式=
=
=
===-2.
答案 -2
6.化简下列各式:
(1)sin(-π)cos π;
(2)sin(-960°)cos 1 470°-cos(-240°)sin(-210°).
解 (1)sin(-π)cos π
=-sin(6π+)cos(π+)=sin cos =.
(2)sin(-960°)cos 1 470°-cos(-240°)sin(-210°)
=-sin(180°+60°+2×360°)cos(30°+4×360°)
+cos(180°+60°)sin(180°+30°)
=sin 60°cos 30°+cos 60°sin 30°=1.
7.已知tan(π+α)=-,求下列各式的值:
(1);
(2)sin(α-7π)·cos(α+5π).
解 由tan(π+α)=-,
得tan α=-,
(1)原式=
==
==-.
(2)原式=sin(-6π+α-π)·cos(4π+α+π)
=sin(α-π)·cos(α+π)
=-sin α(-cos α)
=sin αcos α=
==-.
能力提升
8.已知n为整数,化简所得的结果是( )
A.tan(nα) B.-tan(nα)
C.tan α D.-tan α
解析 当n为偶数时,原式==tan α;
当n为奇数时,原式==tan α.故选C.
答案 C
9.设f(x)=asin(πx+α)+bcos(πx+β)+4,其中a,b,α,β∈R,且ab≠0,α≠kπ(k∈Z).若f(2 009)=5,则f(2 017)等于( )
A.4 B.3
C.-5 D.5
解析 f(2 009)=-(asin α+bcos β)+4=5,
f(2 017)=-(asin α+bcos β)+4=5.
答案 D
10.若cos(π+α)=-,π<α<2π,则sin(α-2π)=________.
解析 由cos(π+α)=-,得cos α=,
故sin(α-2π)=sin α=-=-
=-(α为第四象限角).
答案 -
11.已知a=tan,b=cos,c=sin,则a,b,c的大小关系是________.
解析 a=-tan=-tan=-,
b=cos=cos=,
c=-sin=-sin=-,
∴b>a>c.
答案 b>a>c
12.若cos(α-π)=-,求
的值.
解 原式=
===-tan α.
∵cos(α-π)=cos(π-α)=-cos α=-,
∴cos α=.∴α为第一象限角或第四象限角.
当α为第一象限角时,cos α=,
sin α==,
∴tan α==,
∴原式=-.
当α为第四象限角时,cos α=,
sin α=-=-,
∴tan α==-,∴原式=.
综上,原式=±.
13.(选做题)在△ABC中,若sin(2π-A)=-sin(π-B),cos A=-cos(π-B),求△ABC的三个内角.
解 由条件得sin A=sin B,cos A=cos B,
平方相加得2cos2A=1,cos A=±,
又∵A∈(0,π),
∴A=或π.
当A=π时,cos B=-<0,
∴B∈,
∴A,B均为钝角,不合题意,舍去.
∴A=,cos B=,
∴B=,∴C=π.
综上所述,A=,B=,C=π.
