1.4.3 正切函数的性质与图象学案
文档属性
| 名称 | 1.4.3 正切函数的性质与图象学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 265.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-16 11:02:17 | ||
图片预览





文档简介
1.4.3 正切函数的性质与图象
内容要求 1.了解正切函数图象的画法,理解并掌握正切函数的性质(重点).2.能利用正切函数的图象及性质解决有关问题(重点、难点).
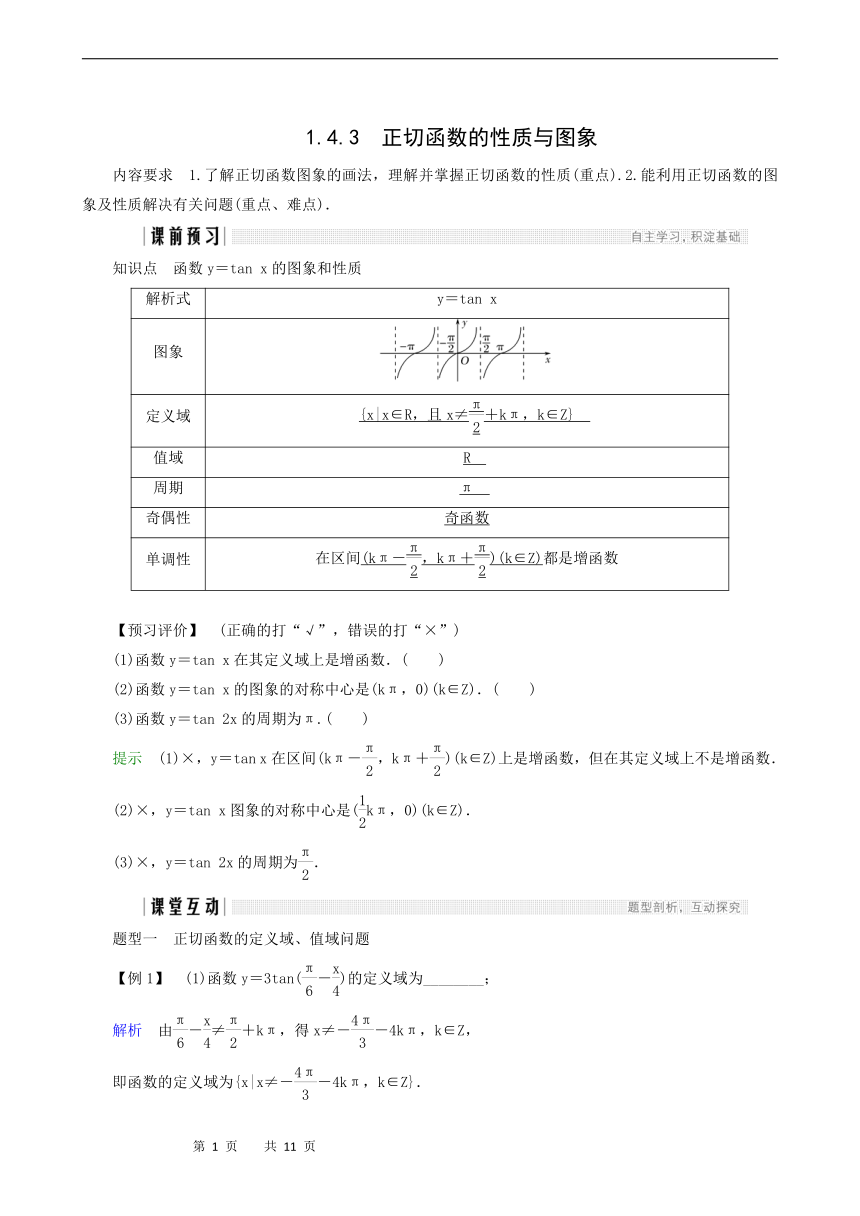
知识点 函数y=tan x的图象和性质
解析式
y=tan x
图象
定义域
{x|x∈R,且x≠+kπ,k∈Z}
值域
R
周期
π
奇偶性
奇函数
单调性
在区间(kπ-,kπ+)(k∈Z)都是增函数
【预习评价】 (正确的打“√”,错误的打“×”)
(1)函数y=tan x在其定义域上是增函数.( )
(2)函数y=tan x的图象的对称中心是(kπ,0)(k∈Z).( )
(3)函数y=tan 2x的周期为π.( )
提示 (1)×,y=tan x在区间(kπ-,kπ+)(k∈Z)上是增函数,但在其定义域上不是增函数.
(2)×,y=tan x图象的对称中心是(kπ,0)(k∈Z).
(3)×,y=tan 2x的周期为.
题型一 正切函数的定义域、值域问题
【例1】 (1)函数y=3tan(-)的定义域为________;
解析 由-≠+kπ,得x≠--4kπ,k∈Z,
即函数的定义域为{x|x≠--4kπ,k∈Z}.
答案 {x|x≠--4kπ,k∈Z}
(2)函数y=tan(2x-),x∈(-,)的值域是________.
解析 ∵-∴tan(2x-)<1,即函数的值域为(-∞,1).
答案 (-∞,1)
规律方法 求正切函数定义域的方法
(1)求与正切函数有关的函数的定义域时,除了求函数定义域的一般要求外,还要保证正切函数y=tan x有意义即x≠+kπ,k∈Z.
(2)求正切型函数y=Atan(ωx+φ)(A≠0,ω>0)的定义域时,要将“ωx+φ”视为一个“整体”,令ωx+φ≠kπ+,k∈Z,解得x.
【训练1】 函数y=tan(sin x)的定义域为______________,值域为______________.
解析 因为-1≤sin x≤1,
所以tan(-1)≤tan(sin x)≤tan 1,
所以y=tan(sin x)的定义域为R,
值域为[-tan 1,tan 1].
答案 R [-tan 1,tan 1]
考查
方向
题型二 正切函数的单调性及应用
方向1 求正切函数的单调区间
【例2-1】 求函数y=tan(-x+)的单调区间.
解 y=tan(-x+)=-tan(x-),
由-+kπ方向2 比较大小
【例2-2】 比较大小:tan(-)和tan(-).
解 ∵tan(-)=-tan(2π-)=tan,
tan(-)=-tan(2π-)=tan.
又0<<<,y=tan x在(0,)内单调递增,
∴tantan(-).
规律方法 1.运用正切函数单调性比较大小的方法
(1)运用函数的周期性或诱导公式将角化到同一单调区间内.
(2)运用单调性比较大小关系.
2.求函数y=Atan(ωx+φ)(A,ω,φ都是常数)的单调区间的方法
(1)若ω>0,由于y=tan x在每一个单调区间上都是增函数,故可用“整体代换”的思想,令kπ-<ωx+φ(2)若ω<0,可利用诱导公式先把y=Atan(ωx+φ)转化为y=Atan[-(-ωx-φ)]=
-Atan(-ωx-φ),即把x的系数化为正值,再利用“整体代换”的思想,求得x的范围即可.
【训练2】 比较tan 1,tan 2,tan 3的大小.
解 ∵1<<2<3<π,根据y=tan x的性质可得:y=tan x在(0,)上单调递增且大于0,在(,π)上单调递增且小于0,∴tan 20,
∴tan 2题型三 正切函数图象性质的应用
【例3】 (1)函数y=tan(2x+)的最小正周期是( )
A.π B.2π
C. D.
解析 最小正周期为T==.
答案 C
(2)画出函数y=|tan x|的图象,并根据图象判断其单调区间、奇偶性、周期性.
解 由y=|tan x|得,
y=
其图象如图:
由图象可知,函数y=|tan x|是偶函数.
函数y=|tan x|的周期T=π,
函数y=|tan x|的单调递增区间[kπ,kπ+)(k∈Z),
单调递减区间为(kπ-,kπ)(k∈Z).
规律方法 1.作出函数y=|f(x)|的图象一般利用图象变换方法,具体步骤是:
(1)保留函数y=f(x)图象在x轴上方的部分;
(2)将函数y=f(x)图象在x轴下方的部分沿x轴向上翻折.
2.若函数为周期函数,可先研究其一个周期上的图象,再利用周期性,延拓到定义域上即可.
【训练3】 (1)下列函数中,既是以π为周期的奇函数,又是(0,)上的增函数的是( )
A.y=tan x B.y=cos x
C.y=tan D.y=|sin x|
解析 由于y=tan x与y=tan 是奇函数,但是只有y=tan x的周期为π,y=cos x与y=|sin x|是偶函数.
答案 A
(2)画出f(x)=tan|x|的图象,并根据其图象判断其单调区间、周期性、奇偶性.
解 f(x)=tan|x|化为
f(x)=
根据y=tan x的图象,作出f(x)=tan|x|的图象,如图所示,
由图象知,f(x)不是周期函数,是偶函数,单调增区间为[0,),(kπ+,kπ+π)(k∈N);单调减区间为(-,0],(kπ-π,kπ-)(k=0,-1,-2,…).
课堂达标
1.函数f(x)=tan(x+)的单调增区间是( )
A.(kπ-,kπ+),k∈Z
B.(kπ,kπ+π),k∈Z
C.(kπ-,kπ+),k∈Z
D.(kπ-,kπ+),k∈Z
解析 由-+kπ答案 C
2.函数y=2tan(-3x+)的最小正周期是( )
A. B.
C. D.π
解析 T==.
答案 B
3.比较大小:tan________tan.
解析 因为tan>0,tan<0,所以tan>tan.
答案 >
4.函数y=tan x(≤x≤,且x≠)的值域是________.
解析 函数y=tan x在[,)上单调递增,在(,]上也是单调递增,所以函数的值域是(-∞,-1]∪[1,+∞).
答案 (-∞,-1]∪[1,+∞)
5.求函数y=tan 2x的定义域、值域和周期,并作出它在区间[-π,π]内的图象.
解 由2x≠+kπ,k∈Z,得x≠+kπ,k∈Z,
即函数的定义域为{x|x≠+kπ,k∈Z},
值域为(-∞,+∞),周期为T=,对应图象如图所示:
课堂小结
1.正切函数的图象
正切函数y=tan x有无数多条渐近线,渐近线方程为x=kπ+,k∈Z,相邻两条渐近线之间都有一支正切曲线,且单调递增.
2.正切函数的性质
(1)正切函数y=tan x的定义域是,
值域是R.
(2)正切函数y=tan x的最小正周期是π,函数y=Atan(ωx+φ) (Aω≠0)的周期为T=.
(3)正切函数在(k∈Z)上递增,不能写成闭区间.正切函数无单调减区间.
基础过关
1.函数y=2tan(2x+)的定义域为( )
A.{x|x≠} B.{x|x≠-}
C.{x|x≠+kπ,k∈Z} D.{x|x≠+kπ,k∈Z}
解析 由2x+≠+kπ,k∈Z,得x≠+kπ,k∈Z,故函数的定义域为{x|x≠+kπ,k∈Z}.
答案 D
2.函数y=tan x+是( )
A.奇函数 B.偶函数
C.既是奇函数又是偶函数 D.既不是奇函数又不是偶函数
解析 函数的定义域是{x|x≠kπ,k∈Z},且tan(-x)+=-tan x-
=-(tan x+),所以函数y=tan x+是奇函数.
答案 A
3.函数y=lg tan x的增区间是( )
A.(k∈Z) B.(k∈Z)
C.(k∈Z) D.(kπ,kπ+π)(k∈Z)
解析 由tan x>0,得kπ答案 B
4.函数y=3tan的对称中心的坐标是________.
解析 由x+= (k∈Z),得x=- (k∈Z).
∴对称中心坐标为 (k∈Z).
答案 (k∈Z)
5.比较大小:tan(-)________tan(-).
解析 tan(-)=tan,tan(-)=tan,
又y=tan x在(,π)内单增,
所以tan即tan(-)答案 <
6.求函数y=-tan2x+4tan x+1,x∈的值域.
解 ∵-≤x≤,
∴-1≤tan x≤1.
令tan x=t,则t∈[-1,1].
∴y=-t2+4t+1=-(t-2)2+5.
∴当t=-1,即x=-时,ymin=-4,
当t=1,即x=时,ymax=4.
故所求函数的值域为[-4,4].
7.设函数f(x)=tan,
(1)求函数f(x)的周期、对称中心;
(2)作出函数f(x)在一个周期内的简图.
解 (1)∵ω=,
∴周期T===2π.
令-=(k∈Z),得x=kπ+(k∈Z),
∴f(x)的对称中心是(k∈Z).
(2)令-=0,则x=.
令-=,则x=.
令-=-,则x=-.
∴函数y=tan的图象与x轴的一个交点坐标是,在这个交点左、右两侧相邻的两条渐近线方程分别是x=-,x=,从而得函数y=f(x)在一个周期内的简图(如图).
能力提升
8.已知函数y=tan ωx在(-,)内是减函数,则( )
A.0<ω≤1 B.-1≤ω<0
C.ω≥1 D.ω≤-1
解析 ∵y=tan ωx在(-,)内是减函数,
∴ω<0且T=≥π.
∴|ω|≤1,即-1≤ω<0.
答案 B
9.函数y=tan x+sin x-|tan x-sin x|在区间内的图象是( )
解析 当当x=π时,y=0;当πsin x,y=2sin x.故选D.
答案 D
10.函数y=tan(+),x∈[0,)∪(,π]的值域为________.
解析 ∵x∈[0,)∪(,π],
∴+∈[,)∪(,],
令t=+,
由y=tan t,t∈[,)∪(,]的图象(如图所示).
可得,所求函数的值域为(-∞,-]∪[,+∞).
答案 (-∞,-]∪[,+∞)
11.若tan(2x-)≤1,则x的取值范围是________.
解析 由题意可得-+kπ<2x-≤+kπ,k∈Z,解之得-+kπ答案 { x|-+kπ12.有两个函数f(x)=asin,g(x)=btan(k>0),它们的周期之和为,且f=g,f=-·g+1.求这两个函数,并求g(x)的单调递增区间.
解 根据题意,可得:
解得
故f(x)=sin,g(x)=tan.
当kπ-<2x-即-所以g(x)的单调递增区间为(k∈Z).
13.(选做题)函数y=sin x与y=tan x的图象在区间[0,2π]上交点的个数是多少?
解 因为当x∈时,tan x>x>sin x,
所以当x∈时,y=sin x与y=tan x没有公共点,因此函数y=sin x与y=tan x在区间[0,2π]内的图象如图所示:
观察图象可知,函数y=tan x与y=sin x在区间[0,2π]上有3个交点.
内容要求 1.了解正切函数图象的画法,理解并掌握正切函数的性质(重点).2.能利用正切函数的图象及性质解决有关问题(重点、难点).
知识点 函数y=tan x的图象和性质
解析式
y=tan x
图象
定义域
{x|x∈R,且x≠+kπ,k∈Z}
值域
R
周期
π
奇偶性
奇函数
单调性
在区间(kπ-,kπ+)(k∈Z)都是增函数
【预习评价】 (正确的打“√”,错误的打“×”)
(1)函数y=tan x在其定义域上是增函数.( )
(2)函数y=tan x的图象的对称中心是(kπ,0)(k∈Z).( )
(3)函数y=tan 2x的周期为π.( )
提示 (1)×,y=tan x在区间(kπ-,kπ+)(k∈Z)上是增函数,但在其定义域上不是增函数.
(2)×,y=tan x图象的对称中心是(kπ,0)(k∈Z).
(3)×,y=tan 2x的周期为.
题型一 正切函数的定义域、值域问题
【例1】 (1)函数y=3tan(-)的定义域为________;
解析 由-≠+kπ,得x≠--4kπ,k∈Z,
即函数的定义域为{x|x≠--4kπ,k∈Z}.
答案 {x|x≠--4kπ,k∈Z}
(2)函数y=tan(2x-),x∈(-,)的值域是________.
解析 ∵-
答案 (-∞,1)
规律方法 求正切函数定义域的方法
(1)求与正切函数有关的函数的定义域时,除了求函数定义域的一般要求外,还要保证正切函数y=tan x有意义即x≠+kπ,k∈Z.
(2)求正切型函数y=Atan(ωx+φ)(A≠0,ω>0)的定义域时,要将“ωx+φ”视为一个“整体”,令ωx+φ≠kπ+,k∈Z,解得x.
【训练1】 函数y=tan(sin x)的定义域为______________,值域为______________.
解析 因为-1≤sin x≤1,
所以tan(-1)≤tan(sin x)≤tan 1,
所以y=tan(sin x)的定义域为R,
值域为[-tan 1,tan 1].
答案 R [-tan 1,tan 1]
考查
方向
题型二 正切函数的单调性及应用
方向1 求正切函数的单调区间
【例2-1】 求函数y=tan(-x+)的单调区间.
解 y=tan(-x+)=-tan(x-),
由-+kπ
【例2-2】 比较大小:tan(-)和tan(-).
解 ∵tan(-)=-tan(2π-)=tan,
tan(-)=-tan(2π-)=tan.
又0<<<,y=tan x在(0,)内单调递增,
∴tan
规律方法 1.运用正切函数单调性比较大小的方法
(1)运用函数的周期性或诱导公式将角化到同一单调区间内.
(2)运用单调性比较大小关系.
2.求函数y=Atan(ωx+φ)(A,ω,φ都是常数)的单调区间的方法
(1)若ω>0,由于y=tan x在每一个单调区间上都是增函数,故可用“整体代换”的思想,令kπ-<ωx+φ
-Atan(-ωx-φ),即把x的系数化为正值,再利用“整体代换”的思想,求得x的范围即可.
【训练2】 比较tan 1,tan 2,tan 3的大小.
解 ∵1<<2<3<π,根据y=tan x的性质可得:y=tan x在(0,)上单调递增且大于0,在(,π)上单调递增且小于0,∴tan 2
∴tan 2
【例3】 (1)函数y=tan(2x+)的最小正周期是( )
A.π B.2π
C. D.
解析 最小正周期为T==.
答案 C
(2)画出函数y=|tan x|的图象,并根据图象判断其单调区间、奇偶性、周期性.
解 由y=|tan x|得,
y=
其图象如图:
由图象可知,函数y=|tan x|是偶函数.
函数y=|tan x|的周期T=π,
函数y=|tan x|的单调递增区间[kπ,kπ+)(k∈Z),
单调递减区间为(kπ-,kπ)(k∈Z).
规律方法 1.作出函数y=|f(x)|的图象一般利用图象变换方法,具体步骤是:
(1)保留函数y=f(x)图象在x轴上方的部分;
(2)将函数y=f(x)图象在x轴下方的部分沿x轴向上翻折.
2.若函数为周期函数,可先研究其一个周期上的图象,再利用周期性,延拓到定义域上即可.
【训练3】 (1)下列函数中,既是以π为周期的奇函数,又是(0,)上的增函数的是( )
A.y=tan x B.y=cos x
C.y=tan D.y=|sin x|
解析 由于y=tan x与y=tan 是奇函数,但是只有y=tan x的周期为π,y=cos x与y=|sin x|是偶函数.
答案 A
(2)画出f(x)=tan|x|的图象,并根据其图象判断其单调区间、周期性、奇偶性.
解 f(x)=tan|x|化为
f(x)=
根据y=tan x的图象,作出f(x)=tan|x|的图象,如图所示,
由图象知,f(x)不是周期函数,是偶函数,单调增区间为[0,),(kπ+,kπ+π)(k∈N);单调减区间为(-,0],(kπ-π,kπ-)(k=0,-1,-2,…).
课堂达标
1.函数f(x)=tan(x+)的单调增区间是( )
A.(kπ-,kπ+),k∈Z
B.(kπ,kπ+π),k∈Z
C.(kπ-,kπ+),k∈Z
D.(kπ-,kπ+),k∈Z
解析 由-+kπ
2.函数y=2tan(-3x+)的最小正周期是( )
A. B.
C. D.π
解析 T==.
答案 B
3.比较大小:tan________tan.
解析 因为tan>0,tan<0,所以tan>tan.
答案 >
4.函数y=tan x(≤x≤,且x≠)的值域是________.
解析 函数y=tan x在[,)上单调递增,在(,]上也是单调递增,所以函数的值域是(-∞,-1]∪[1,+∞).
答案 (-∞,-1]∪[1,+∞)
5.求函数y=tan 2x的定义域、值域和周期,并作出它在区间[-π,π]内的图象.
解 由2x≠+kπ,k∈Z,得x≠+kπ,k∈Z,
即函数的定义域为{x|x≠+kπ,k∈Z},
值域为(-∞,+∞),周期为T=,对应图象如图所示:
课堂小结
1.正切函数的图象
正切函数y=tan x有无数多条渐近线,渐近线方程为x=kπ+,k∈Z,相邻两条渐近线之间都有一支正切曲线,且单调递增.
2.正切函数的性质
(1)正切函数y=tan x的定义域是,
值域是R.
(2)正切函数y=tan x的最小正周期是π,函数y=Atan(ωx+φ) (Aω≠0)的周期为T=.
(3)正切函数在(k∈Z)上递增,不能写成闭区间.正切函数无单调减区间.
基础过关
1.函数y=2tan(2x+)的定义域为( )
A.{x|x≠} B.{x|x≠-}
C.{x|x≠+kπ,k∈Z} D.{x|x≠+kπ,k∈Z}
解析 由2x+≠+kπ,k∈Z,得x≠+kπ,k∈Z,故函数的定义域为{x|x≠+kπ,k∈Z}.
答案 D
2.函数y=tan x+是( )
A.奇函数 B.偶函数
C.既是奇函数又是偶函数 D.既不是奇函数又不是偶函数
解析 函数的定义域是{x|x≠kπ,k∈Z},且tan(-x)+=-tan x-
=-(tan x+),所以函数y=tan x+是奇函数.
答案 A
3.函数y=lg tan x的增区间是( )
A.(k∈Z) B.(k∈Z)
C.(k∈Z) D.(kπ,kπ+π)(k∈Z)
解析 由tan x>0,得kπ
4.函数y=3tan的对称中心的坐标是________.
解析 由x+= (k∈Z),得x=- (k∈Z).
∴对称中心坐标为 (k∈Z).
答案 (k∈Z)
5.比较大小:tan(-)________tan(-).
解析 tan(-)=tan,tan(-)=tan,
又y=tan x在(,π)内单增,
所以tan
6.求函数y=-tan2x+4tan x+1,x∈的值域.
解 ∵-≤x≤,
∴-1≤tan x≤1.
令tan x=t,则t∈[-1,1].
∴y=-t2+4t+1=-(t-2)2+5.
∴当t=-1,即x=-时,ymin=-4,
当t=1,即x=时,ymax=4.
故所求函数的值域为[-4,4].
7.设函数f(x)=tan,
(1)求函数f(x)的周期、对称中心;
(2)作出函数f(x)在一个周期内的简图.
解 (1)∵ω=,
∴周期T===2π.
令-=(k∈Z),得x=kπ+(k∈Z),
∴f(x)的对称中心是(k∈Z).
(2)令-=0,则x=.
令-=,则x=.
令-=-,则x=-.
∴函数y=tan的图象与x轴的一个交点坐标是,在这个交点左、右两侧相邻的两条渐近线方程分别是x=-,x=,从而得函数y=f(x)在一个周期内的简图(如图).
能力提升
8.已知函数y=tan ωx在(-,)内是减函数,则( )
A.0<ω≤1 B.-1≤ω<0
C.ω≥1 D.ω≤-1
解析 ∵y=tan ωx在(-,)内是减函数,
∴ω<0且T=≥π.
∴|ω|≤1,即-1≤ω<0.
答案 B
9.函数y=tan x+sin x-|tan x-sin x|在区间内的图象是( )
解析 当
答案 D
10.函数y=tan(+),x∈[0,)∪(,π]的值域为________.
解析 ∵x∈[0,)∪(,π],
∴+∈[,)∪(,],
令t=+,
由y=tan t,t∈[,)∪(,]的图象(如图所示).
可得,所求函数的值域为(-∞,-]∪[,+∞).
答案 (-∞,-]∪[,+∞)
11.若tan(2x-)≤1,则x的取值范围是________.
解析 由题意可得-+kπ<2x-≤+kπ,k∈Z,解之得-+kπ
解 根据题意,可得:
解得
故f(x)=sin,g(x)=tan.
当kπ-<2x-
13.(选做题)函数y=sin x与y=tan x的图象在区间[0,2π]上交点的个数是多少?
解 因为当x∈时,tan x>x>sin x,
所以当x∈时,y=sin x与y=tan x没有公共点,因此函数y=sin x与y=tan x在区间[0,2π]内的图象如图所示:
观察图象可知,函数y=tan x与y=sin x在区间[0,2π]上有3个交点.
