1.6 三角函数模型的简单应用学案
文档属性
| 名称 | 1.6 三角函数模型的简单应用学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 426.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-16 00:00:00 | ||
图片预览



文档简介
§1.6 三角函数模型的简单应用
内容要求 1.会用三角函数解决一些简单的实际问题(重点、难点).2.体会三角函数是描述周期变化现象的重要函数模型(重点).
知识点 三角函数的应用
1.根据实际问题的图象求出函数解析式.
2.三角函数是描述现实世界中周期现象的一种数学模型,因此可将实际问题抽象为与三角函数有关的简单函数模型.
3.利用搜集的数据,作出散点图,通过观察散点图进行函数拟合而得到函数模型,最后利用这个函数模型来解决相应的实际问题.
【预习评价】
一根长l cm的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(cm)与时间t(s)的函数关系式为s=3cos,其中g是重力加速度,当小球摆动的周期是1 s时,线长l=________ cm.
解析 T==1,
∴ =2π,
∴l=.
答案
题型一 三角函数图象与解析式的对应问题
【例1】 (1)已知函数y=sin ax+b(a>0)的图象如图所示,则函数y=loga(x+b)的图象可能是( )
解析 由函数的图象可得02π-π,
∴0答案 C
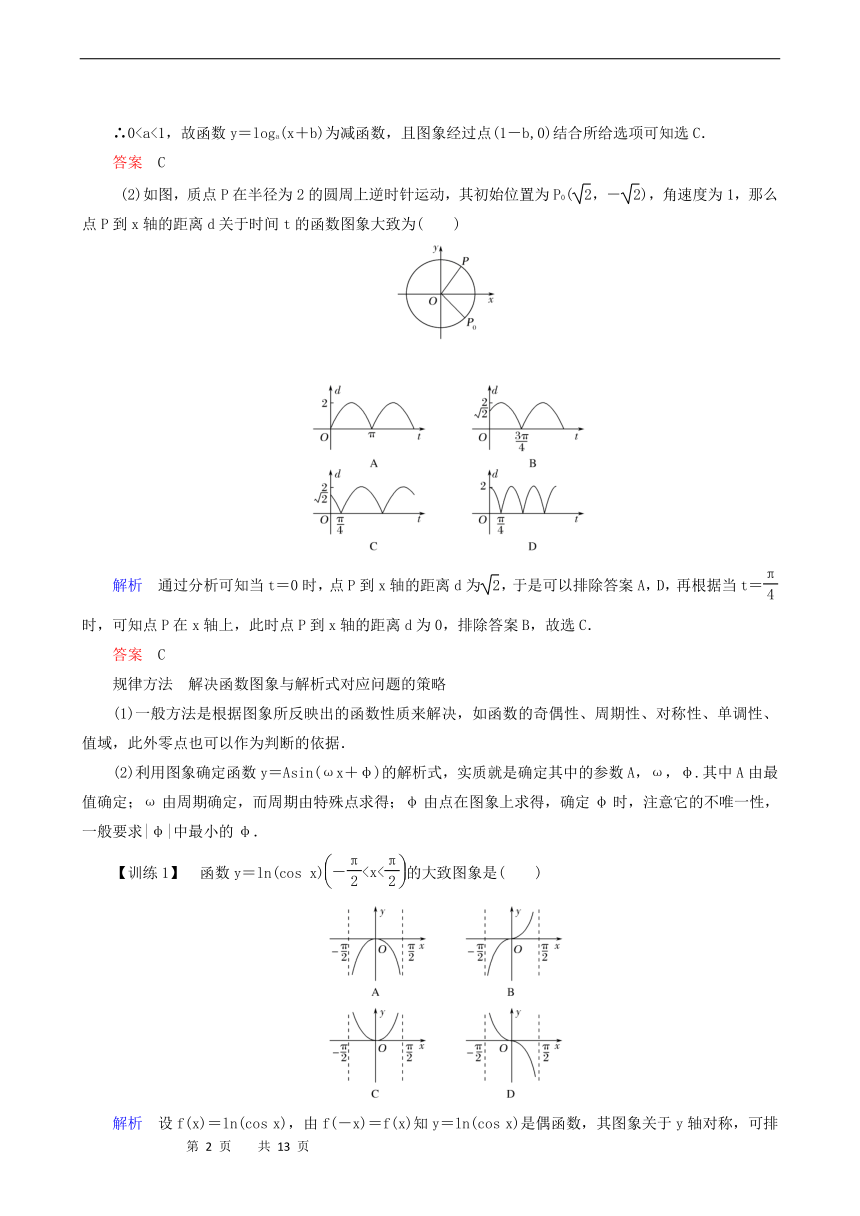
(2)如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0(,-),角速度为1,那么点P到x轴的距离d关于时间t的函数图象大致为( )
解析 通过分析可知当t=0时,点P到x轴的距离d为,于是可以排除答案A,D,再根据当t=时,可知点P在x轴上,此时点P到x轴的距离d为0,排除答案B,故选C.
答案 C
规律方法 解决函数图象与解析式对应问题的策略
(1)一般方法是根据图象所反映出的函数性质来解决,如函数的奇偶性、周期性、对称性、单调性、值域,此外零点也可以作为判断的依据.
(2)利用图象确定函数y=Asin(ωx+φ)的解析式,实质就是确定其中的参数A,ω,φ.其中A由最值确定;ω由周期确定,而周期由特殊点求得;φ由点在图象上求得,确定φ时,注意它的不唯一性,一般要求|φ|中最小的φ.
【训练1】 函数y=ln(cos x)的大致图象是( )
解析 设f(x)=ln(cos x),由f(-x)=f(x)知y=ln(cos x)是偶函数,其图象关于y轴对称,可排除B,D,又当-答案 A
题型二 三角函数在物理学中的应用
【例2】 已知电流I与时间t的关系为I=Asin(ωt+φ).
(1)如图所示的是I=Asin(ωt+φ)(ω>0,|φ|<)在一个周期内的图象,根据图中数据求I=Asin(ωt+φ)的解析式;
(2)如果t在任意一段秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,那么ω的最小正整数值是多少?
解 (1)由题图知A=300,设t1=-,t2=,
则周期T=2(t2-t1)=2=.
∴ω==150π.
又当t=时,I=0,即sin=0,
而|φ|<,∴φ=.
故所求的解析式为I=300sin.
(2)依题意,周期T≤,
即≤(ω>0),
∴ω≥300π>942,又ω∈N*,
故所求最小正整数ω=943.
规律方法 处理物理学问题的策略
(1)常涉及的物理学问题有单摆、光波、电流、机械波等,其共同的特点是具有周期性.
(2)明确物理概念的意义,此类问题往往涉及诸如频率、振幅等概念,因此要熟知其意义并与对应的三角函数知识结合解题.
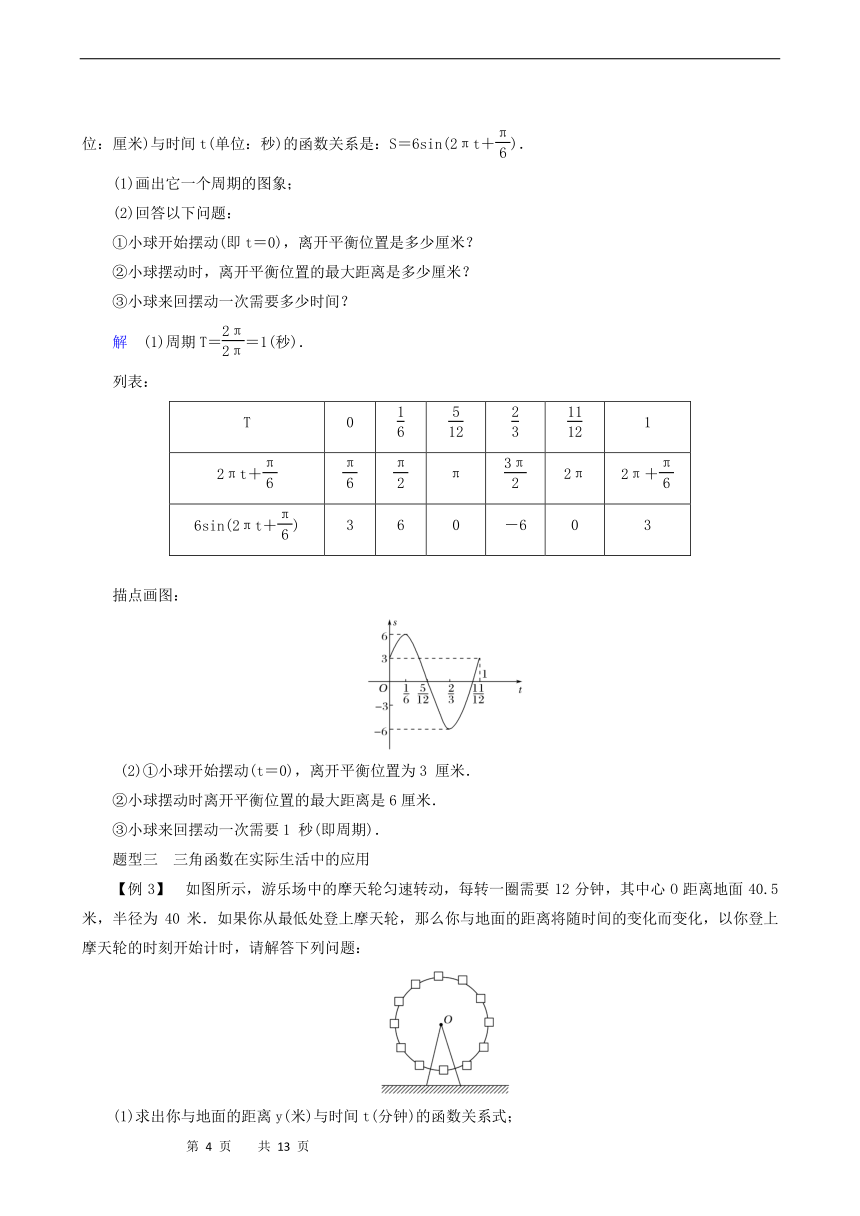
【训练2】 一根细线的一端固定,另一端悬挂一个小球,小球来回摆动时,离开平衡位置的位移S(单位:厘米)与时间t(单位:秒)的函数关系是:S=6sin(2πt+).
(1)画出它一个周期的图象;
(2)回答以下问题:
①小球开始摆动(即t=0),离开平衡位置是多少厘米?
②小球摆动时,离开平衡位置的最大距离是多少厘米?
③小球来回摆动一次需要多少时间?
解 (1)周期T==1(秒).
列表:
T
0
1
2πt+
π
2π
2π+
6sin(2πt+)
3
6
0
-6
0
3
描点画图:
(2)①小球开始摆动(t=0),离开平衡位置为3 厘米.
②小球摆动时离开平衡位置的最大距离是6厘米.
③小球来回摆动一次需要1 秒(即周期).
题型三 三角函数在实际生活中的应用
【例3】 如图所示,游乐场中的摩天轮匀速转动,每转一圈需要12分钟,其中心O距离地面40.5米,半径为40米.如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时,请解答下列问题:
(1)求出你与地面的距离y(米)与时间t(分钟)的函数关系式;
(2)当你第4次距离地面60.5米时,用了多长时间?
解 (1)由已知可设y=40.5-40cos ωt,t≥0,由周期为12分钟可知,当t=6时,摩天轮第1次到达最高点,即此函数第1次取得最大值,所以6ω=π,即ω=,所以y=40.5-40cost(t≥0).
(2)设转第1圈时,第t0分钟时距离地面60.5米.由60.5=40.5-40cost0,得cost0=-,所以t0=或t0=,解得t0=4或t0=8,所以t=8(分钟)时,第2次距地面60.5米,故第4次距离地面60.5米时,用了12+8=20(分钟).
规律方法 解三角函数应用问题的基本步骤
【训练3】 一物体相对于某一固定位置的位移y(cm)和时间t(s)之间的一组对应值如下表所示,则可近似地描述该物体的位置y和时间t之间的关系的一个三角函数式为________.
t
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
y
-4.0
-2.8
0.0
2.8
4.0
2.8
0.0
-2.8
-4.0
解析 设y=Asin(ωx+φ),则从表中可以得到 A=4,T=0.8,ω==,又由4sin φ=-4.0,可得sin φ=-1,即φ=-,故y=4sin(t-),即y=-4cost.
答案 y=-4cost
课堂达标
1.函数y=|sin(x+)|的最小正周期为( )
A.2π B.π
C.4π D.
解析 易知函数y=sin(x+)的周期为4π,故y=|sin(x+)|的最小正周期为×4π=2π.
答案 A
2.如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin+k,据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5 B.6
C.8 D.10
解析 由题意可知当sin(x+φ)取最小值-1时,
函数取最小值ymin=-3+k=2,得k=5,
∴y=3sin(x+φ)+5,当sin(x+φ)取最大值1时,
函数取最大值ymax=3+5=8.
答案 C
3.电流强度I(A)随时间t(s)变化的关系式是I=5sin,则当t= s时,电流强度I为( )
A.5 A B.2.5 A
C.2 A D.-5 A
解析 当t=时,I=5sin(100π×+)=5sin(+)=5cos==2.5 A.
答案 B
4.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y=a+Acos (x=1,2,3,…,12,A>0)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值为________℃.
解析 由题意得
∴
∴y=23+5cos,
当x=10时,y=23+5×=20.5.
答案 20.5
5.如图所示,一个摩天轮半径为10 m,轮子的底部在地面上2 m处,如果此摩天轮按逆时针转动,每30 s转一圈,且当摩天轮上某人经过点P处(点P与摩天轮中心高度相同)时开始计时.
(1)求此人相对于地面的高度关于时间的关系式;
(2)在摩天轮转动的一圈内,约有多长时间此人相对于地面的高度不小于17 m.
解 (1)设在t s时,摩天轮上某人在高h m处.这时此人所转过的角为 t= t,故在t s时,此人相对于地面的高度为h=10sin t+12(t≥0).
(2)由10sint+12≥17,
得sint≥,
则≤t≤.
故此人有10 s相对于地面的高度不小于17 m.
课堂小结
1.三角函数模型是研究周期现象最重要的数学模型,三角函数模型在研究物理 、生物、自然界中的周期现象(运动)有着广泛的应用.
2.三角函数模型构建的步骤:
(1)收集数据,观察数据,发现是否具有周期性的重复现象.
(2)制作散点图,选择函数模型进行拟合.
(3)利用三角函数模型解决实际问题.
(4)根据问题的实际意义,对答案的合理性进行检验.
基础过关
1.函数f(x)的部分图象如图所示,则f(x)的解析式可以是( )
A.f(x)=x+sin x B.f(x)=
C.f(x)=x cos x D.f(x)=x··
解析 由题图象可知f(x)是奇函数,可排除选项D,又f()=0,可排除A,f(0)=0,可排除B,故选C.
答案 C
2.如图所示,有一广告气球,直径为6 m,放在公司大楼上空,当行人仰望气球中心的仰角∠BAC=30°时,测得气球的视角为β=1°,当θ很小时,可取sin θ≈θ,试估算气球的高BC的值约为( )
A.70 m B.86 m
C.102 m D.118 m
解析 AC==≈×180≈172(m),又∠BAC=30°,∴BC=AC=86 m.
答案 B
3.如图所示,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )
解析 设所对的圆心角为α,则α=l,
弦AP的长d=2·|OA|·sin,
即有d=f(l)=2sin .
答案 C
4.已知某种交流电流I(A)随时间t(s)的变化规律可以拟合为函数I=5sin,t∈[0,+∞),则这种交流电在0.5 s内往复运动________次.
解析 据I=5sin(100πt-)知ω=100π rad/s,
该电流的周期为T===0.02 s,
则这种交流电电流在0.5 s内往复运行次数为
n=2·=2× s=50(次).
答案 50
5.某时钟的秒针端点A到中心点O的距离为5 cm,秒针均匀地绕点O旋转,当时间t=0时,点A与钟面上标12的点B重合,将A,B两点的距离d(cm)表示成t(s)的函数,则d=__________,其中t∈[0,60].
解析 将解析式可写为d=Asin(ωt+φ)的形式,由题意易知A=10,当t=0时,d=0,得φ=0;当t=30时,d=10,
可得ω=,所以d=10sin .
答案 10sin
6.如图所示,某地夏天从8~14时的用电量变化曲线近似满足函数y=Asin(ωx+φ)+b(0<φ<).
(1)求这一天的最大用电量及最小用电量;
(2)写出这段曲线的函数解析式.
解 (1)最大用电量为50万kW·h,
最小用电量为30万kW·h.
(2)观察图象可知从8~14时的图象是y=Asin(ωx+φ)+b的半个周期的图象,
∴A=×(50-30)=10,b=×(50+30)=40.
∵×=14-8,
∴ω=.∴y=10sin+40.
将x=8,y=30代入上式,
又∵0<φ<,∴解得φ=.
∴所求解析式为y=10sin+40,x∈[8,14].
7.已知某海滨浴场海浪的高度y(米)是时间t(0≤t≤24,单位:小时)的函数,记作:y=f(t),下表是某日各时的浪高数据:
t(时)
0
3
6
9
12
15
18
21
24
y(米)
1.5
1.0
0.5
1.0
1.5
1.0
0.5
0.99
1.5
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acos ωt+b.
(1)根据以上数据,求函数y=Acos ωt+b的最小正周期T,振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8∶00至晚上20∶00之间,有多少时间可供冲浪者进行运动?
解 (1)由表中数据知周期T=12,
∴ω===,
由t=0,y=1.5,得A+b=1.5.
由t=3,y=1.0,得b=1.0.
∴A=0.5,b=1,∴y=cos t+1.
(2)由题意知,当y>1时才可对冲浪者开放,
∴cos t+1>1,
∴cos t>0,∴2kπ-即12k-3∵0≤t≤24,故可令①中k分别为0,1,2,
得0≤t<3或9∴在规定时间上午8∶00至晚上20∶00之间,有6个小时时间可供冲浪者运动,即上午9∶00至下午3∶00.
能力提升
8.动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
A.[0,1] B.[1,7]
C.[7,12] D.[0,1]和[7,12]
解析 设动点A与x轴正方向夹角为α,则t=0时,α=,每秒钟旋转,在t∈[0,1]上,α∈[,],在[7,12]上α∈[,],动点A的纵坐标y关于t都是单调递增的,故选D.
答案 D
9.商场人流量被定义为每分钟通过入口的人数,五一某商场的人流量满足函数F(t)=50+4sin(t≥0),则在下列哪个时间段内人流量是增加的( )
A.[0,5] B.[5,10]
C.[10,15] D.[15,20]
解析 由2kπ-≤≤2kπ+,k∈Z,知函数F(t)的增区间为[4kπ-π,4kπ+π],k∈Z.当k=1时,t∈[3π,5π],而[10,15]?[3π,5π],故选C.
答案 C
10.一种波的波形为函数y=-sinx的图象,若其在区间[0,t]上至少有2个波峰(图象的最高点),则正整数t的最小值是________.
解析 由T==4可知此波形的函数周期为4,显然当0≤x≤1时函数单调递减,1答案 7
11.设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,|KL|=1,则f()的值为________.
解析 取K,L中点N,则MN=,
因此A=.由T=2得ω=π.
∵函数为偶函数,0<φ<π,∴φ=,
∴f(x)=cos πx,∴f()=cos =.
答案
12.为迎接夏季旅游旺季的到来,少林寺单独设置了一个专门安排旅客住宿的客栈,寺庙的工作人员发现为游客准备的食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入.为此他们统计每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数会发生周期性的变化,并且有以下规律:
①每年相同的月份,入住客栈的游客人数基本相同;
②入住客栈的游客人数在2月份最少,在8月份最多,相差约400人;
③2月份入住客栈的游客约为100人,随后逐月递增直到8月份达到最多.
(1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系;
(2)请问哪几个月份要准备400份以上的食物?
解 (1)设该函数为f(x)=Asin(ωx+φ)+B(A>0,ω>0,0<|φ|<π),根据条件①,可知这个函数的周期是12;由②可知,f(2)最小,f(8)最大,且f(8)-f(2)=400,故该函数的振幅为200;由③可知,f(x)在[2,8]上单调递增,且f(2)=100,所以f(8)=500.
根据上述分析可得,=12,
故ω=,且解得
根据分析可知,当x=2时,f(x)最小,
当x=8时,f(x)最大,
故sin=-1,且sin=1.
又因为0<|φ|<π,故φ=-.
所以入住客栈的游客人数与月份之间的关系式为
f(x)=200sin+300.
(2)由条件可知,200sin+300≥400,化简得
sin≥?2kπ+≤x-≤2kπ+,k∈Z,
解得12k+6≤x≤12k+10,k∈Z.
因为x∈N*,且1≤x≤12,所以x=6,7,8,9,10.
即只有6,7,8,9,10五个月份要准备400份以上的食物.
13.(选做题)下表是某地某年月平均气温(华氏):
月份
1
2
3
4
5
6
平均气温
21.4
26.0
36.0
48.8
59.1
68.6
月份
7
8
9
10
11
12
平均气温
73.0
71.9
64.7
53.5
39.8
27.7
以月份为x轴(x=月份-1),以平均气温为y轴.
(1)用正弦曲线去拟合这些数据;
(2)估计这个正弦曲线的周期T和振幅A;
(3)下面三个函数模型中,哪一个最适合这些数据?
①=cos;②=cos;③=cos.
解 (1)如图.
(2)最低气温为1月份21.4,最高气温为7月份73.0,
故=7-1=6,所以T=12.
因为2A的值等于最高气温与最低气温的差,
即2A=73.0-21.4=51.6,所以A=25.8.
(3)因为x=月份-1,
所以不妨取x=2-1=1,y=26.0.
代入①,得=>1≠cos,故①不适合;代入②,得=<0≠cos,故②不适合.所以应选③.
内容要求 1.会用三角函数解决一些简单的实际问题(重点、难点).2.体会三角函数是描述周期变化现象的重要函数模型(重点).
知识点 三角函数的应用
1.根据实际问题的图象求出函数解析式.
2.三角函数是描述现实世界中周期现象的一种数学模型,因此可将实际问题抽象为与三角函数有关的简单函数模型.
3.利用搜集的数据,作出散点图,通过观察散点图进行函数拟合而得到函数模型,最后利用这个函数模型来解决相应的实际问题.
【预习评价】
一根长l cm的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(cm)与时间t(s)的函数关系式为s=3cos,其中g是重力加速度,当小球摆动的周期是1 s时,线长l=________ cm.
解析 T==1,
∴ =2π,
∴l=.
答案
题型一 三角函数图象与解析式的对应问题
【例1】 (1)已知函数y=sin ax+b(a>0)的图象如图所示,则函数y=loga(x+b)的图象可能是( )
解析 由函数的图象可得0
∴0
(2)如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0(,-),角速度为1,那么点P到x轴的距离d关于时间t的函数图象大致为( )
解析 通过分析可知当t=0时,点P到x轴的距离d为,于是可以排除答案A,D,再根据当t=时,可知点P在x轴上,此时点P到x轴的距离d为0,排除答案B,故选C.
答案 C
规律方法 解决函数图象与解析式对应问题的策略
(1)一般方法是根据图象所反映出的函数性质来解决,如函数的奇偶性、周期性、对称性、单调性、值域,此外零点也可以作为判断的依据.
(2)利用图象确定函数y=Asin(ωx+φ)的解析式,实质就是确定其中的参数A,ω,φ.其中A由最值确定;ω由周期确定,而周期由特殊点求得;φ由点在图象上求得,确定φ时,注意它的不唯一性,一般要求|φ|中最小的φ.
【训练1】 函数y=ln(cos x)的大致图象是( )
解析 设f(x)=ln(cos x),由f(-x)=f(x)知y=ln(cos x)是偶函数,其图象关于y轴对称,可排除B,D,又当-
题型二 三角函数在物理学中的应用
【例2】 已知电流I与时间t的关系为I=Asin(ωt+φ).
(1)如图所示的是I=Asin(ωt+φ)(ω>0,|φ|<)在一个周期内的图象,根据图中数据求I=Asin(ωt+φ)的解析式;
(2)如果t在任意一段秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,那么ω的最小正整数值是多少?
解 (1)由题图知A=300,设t1=-,t2=,
则周期T=2(t2-t1)=2=.
∴ω==150π.
又当t=时,I=0,即sin=0,
而|φ|<,∴φ=.
故所求的解析式为I=300sin.
(2)依题意,周期T≤,
即≤(ω>0),
∴ω≥300π>942,又ω∈N*,
故所求最小正整数ω=943.
规律方法 处理物理学问题的策略
(1)常涉及的物理学问题有单摆、光波、电流、机械波等,其共同的特点是具有周期性.
(2)明确物理概念的意义,此类问题往往涉及诸如频率、振幅等概念,因此要熟知其意义并与对应的三角函数知识结合解题.
【训练2】 一根细线的一端固定,另一端悬挂一个小球,小球来回摆动时,离开平衡位置的位移S(单位:厘米)与时间t(单位:秒)的函数关系是:S=6sin(2πt+).
(1)画出它一个周期的图象;
(2)回答以下问题:
①小球开始摆动(即t=0),离开平衡位置是多少厘米?
②小球摆动时,离开平衡位置的最大距离是多少厘米?
③小球来回摆动一次需要多少时间?
解 (1)周期T==1(秒).
列表:
T
0
1
2πt+
π
2π
2π+
6sin(2πt+)
3
6
0
-6
0
3
描点画图:
(2)①小球开始摆动(t=0),离开平衡位置为3 厘米.
②小球摆动时离开平衡位置的最大距离是6厘米.
③小球来回摆动一次需要1 秒(即周期).
题型三 三角函数在实际生活中的应用
【例3】 如图所示,游乐场中的摩天轮匀速转动,每转一圈需要12分钟,其中心O距离地面40.5米,半径为40米.如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时,请解答下列问题:
(1)求出你与地面的距离y(米)与时间t(分钟)的函数关系式;
(2)当你第4次距离地面60.5米时,用了多长时间?
解 (1)由已知可设y=40.5-40cos ωt,t≥0,由周期为12分钟可知,当t=6时,摩天轮第1次到达最高点,即此函数第1次取得最大值,所以6ω=π,即ω=,所以y=40.5-40cost(t≥0).
(2)设转第1圈时,第t0分钟时距离地面60.5米.由60.5=40.5-40cost0,得cost0=-,所以t0=或t0=,解得t0=4或t0=8,所以t=8(分钟)时,第2次距地面60.5米,故第4次距离地面60.5米时,用了12+8=20(分钟).
规律方法 解三角函数应用问题的基本步骤
【训练3】 一物体相对于某一固定位置的位移y(cm)和时间t(s)之间的一组对应值如下表所示,则可近似地描述该物体的位置y和时间t之间的关系的一个三角函数式为________.
t
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
y
-4.0
-2.8
0.0
2.8
4.0
2.8
0.0
-2.8
-4.0
解析 设y=Asin(ωx+φ),则从表中可以得到 A=4,T=0.8,ω==,又由4sin φ=-4.0,可得sin φ=-1,即φ=-,故y=4sin(t-),即y=-4cost.
答案 y=-4cost
课堂达标
1.函数y=|sin(x+)|的最小正周期为( )
A.2π B.π
C.4π D.
解析 易知函数y=sin(x+)的周期为4π,故y=|sin(x+)|的最小正周期为×4π=2π.
答案 A
2.如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin+k,据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5 B.6
C.8 D.10
解析 由题意可知当sin(x+φ)取最小值-1时,
函数取最小值ymin=-3+k=2,得k=5,
∴y=3sin(x+φ)+5,当sin(x+φ)取最大值1时,
函数取最大值ymax=3+5=8.
答案 C
3.电流强度I(A)随时间t(s)变化的关系式是I=5sin,则当t= s时,电流强度I为( )
A.5 A B.2.5 A
C.2 A D.-5 A
解析 当t=时,I=5sin(100π×+)=5sin(+)=5cos==2.5 A.
答案 B
4.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y=a+Acos (x=1,2,3,…,12,A>0)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值为________℃.
解析 由题意得
∴
∴y=23+5cos,
当x=10时,y=23+5×=20.5.
答案 20.5
5.如图所示,一个摩天轮半径为10 m,轮子的底部在地面上2 m处,如果此摩天轮按逆时针转动,每30 s转一圈,且当摩天轮上某人经过点P处(点P与摩天轮中心高度相同)时开始计时.
(1)求此人相对于地面的高度关于时间的关系式;
(2)在摩天轮转动的一圈内,约有多长时间此人相对于地面的高度不小于17 m.
解 (1)设在t s时,摩天轮上某人在高h m处.这时此人所转过的角为 t= t,故在t s时,此人相对于地面的高度为h=10sin t+12(t≥0).
(2)由10sint+12≥17,
得sint≥,
则≤t≤.
故此人有10 s相对于地面的高度不小于17 m.
课堂小结
1.三角函数模型是研究周期现象最重要的数学模型,三角函数模型在研究物理 、生物、自然界中的周期现象(运动)有着广泛的应用.
2.三角函数模型构建的步骤:
(1)收集数据,观察数据,发现是否具有周期性的重复现象.
(2)制作散点图,选择函数模型进行拟合.
(3)利用三角函数模型解决实际问题.
(4)根据问题的实际意义,对答案的合理性进行检验.
基础过关
1.函数f(x)的部分图象如图所示,则f(x)的解析式可以是( )
A.f(x)=x+sin x B.f(x)=
C.f(x)=x cos x D.f(x)=x··
解析 由题图象可知f(x)是奇函数,可排除选项D,又f()=0,可排除A,f(0)=0,可排除B,故选C.
答案 C
2.如图所示,有一广告气球,直径为6 m,放在公司大楼上空,当行人仰望气球中心的仰角∠BAC=30°时,测得气球的视角为β=1°,当θ很小时,可取sin θ≈θ,试估算气球的高BC的值约为( )
A.70 m B.86 m
C.102 m D.118 m
解析 AC==≈×180≈172(m),又∠BAC=30°,∴BC=AC=86 m.
答案 B
3.如图所示,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )
解析 设所对的圆心角为α,则α=l,
弦AP的长d=2·|OA|·sin,
即有d=f(l)=2sin .
答案 C
4.已知某种交流电流I(A)随时间t(s)的变化规律可以拟合为函数I=5sin,t∈[0,+∞),则这种交流电在0.5 s内往复运动________次.
解析 据I=5sin(100πt-)知ω=100π rad/s,
该电流的周期为T===0.02 s,
则这种交流电电流在0.5 s内往复运行次数为
n=2·=2× s=50(次).
答案 50
5.某时钟的秒针端点A到中心点O的距离为5 cm,秒针均匀地绕点O旋转,当时间t=0时,点A与钟面上标12的点B重合,将A,B两点的距离d(cm)表示成t(s)的函数,则d=__________,其中t∈[0,60].
解析 将解析式可写为d=Asin(ωt+φ)的形式,由题意易知A=10,当t=0时,d=0,得φ=0;当t=30时,d=10,
可得ω=,所以d=10sin .
答案 10sin
6.如图所示,某地夏天从8~14时的用电量变化曲线近似满足函数y=Asin(ωx+φ)+b(0<φ<).
(1)求这一天的最大用电量及最小用电量;
(2)写出这段曲线的函数解析式.
解 (1)最大用电量为50万kW·h,
最小用电量为30万kW·h.
(2)观察图象可知从8~14时的图象是y=Asin(ωx+φ)+b的半个周期的图象,
∴A=×(50-30)=10,b=×(50+30)=40.
∵×=14-8,
∴ω=.∴y=10sin+40.
将x=8,y=30代入上式,
又∵0<φ<,∴解得φ=.
∴所求解析式为y=10sin+40,x∈[8,14].
7.已知某海滨浴场海浪的高度y(米)是时间t(0≤t≤24,单位:小时)的函数,记作:y=f(t),下表是某日各时的浪高数据:
t(时)
0
3
6
9
12
15
18
21
24
y(米)
1.5
1.0
0.5
1.0
1.5
1.0
0.5
0.99
1.5
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acos ωt+b.
(1)根据以上数据,求函数y=Acos ωt+b的最小正周期T,振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8∶00至晚上20∶00之间,有多少时间可供冲浪者进行运动?
解 (1)由表中数据知周期T=12,
∴ω===,
由t=0,y=1.5,得A+b=1.5.
由t=3,y=1.0,得b=1.0.
∴A=0.5,b=1,∴y=cos t+1.
(2)由题意知,当y>1时才可对冲浪者开放,
∴cos t+1>1,
∴cos t>0,∴2kπ-
得0≤t<3或9
能力提升
8.动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
A.[0,1] B.[1,7]
C.[7,12] D.[0,1]和[7,12]
解析 设动点A与x轴正方向夹角为α,则t=0时,α=,每秒钟旋转,在t∈[0,1]上,α∈[,],在[7,12]上α∈[,],动点A的纵坐标y关于t都是单调递增的,故选D.
答案 D
9.商场人流量被定义为每分钟通过入口的人数,五一某商场的人流量满足函数F(t)=50+4sin(t≥0),则在下列哪个时间段内人流量是增加的( )
A.[0,5] B.[5,10]
C.[10,15] D.[15,20]
解析 由2kπ-≤≤2kπ+,k∈Z,知函数F(t)的增区间为[4kπ-π,4kπ+π],k∈Z.当k=1时,t∈[3π,5π],而[10,15]?[3π,5π],故选C.
答案 C
10.一种波的波形为函数y=-sinx的图象,若其在区间[0,t]上至少有2个波峰(图象的最高点),则正整数t的最小值是________.
解析 由T==4可知此波形的函数周期为4,显然当0≤x≤1时函数单调递减,1
11.设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,|KL|=1,则f()的值为________.
解析 取K,L中点N,则MN=,
因此A=.由T=2得ω=π.
∵函数为偶函数,0<φ<π,∴φ=,
∴f(x)=cos πx,∴f()=cos =.
答案
12.为迎接夏季旅游旺季的到来,少林寺单独设置了一个专门安排旅客住宿的客栈,寺庙的工作人员发现为游客准备的食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入.为此他们统计每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数会发生周期性的变化,并且有以下规律:
①每年相同的月份,入住客栈的游客人数基本相同;
②入住客栈的游客人数在2月份最少,在8月份最多,相差约400人;
③2月份入住客栈的游客约为100人,随后逐月递增直到8月份达到最多.
(1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系;
(2)请问哪几个月份要准备400份以上的食物?
解 (1)设该函数为f(x)=Asin(ωx+φ)+B(A>0,ω>0,0<|φ|<π),根据条件①,可知这个函数的周期是12;由②可知,f(2)最小,f(8)最大,且f(8)-f(2)=400,故该函数的振幅为200;由③可知,f(x)在[2,8]上单调递增,且f(2)=100,所以f(8)=500.
根据上述分析可得,=12,
故ω=,且解得
根据分析可知,当x=2时,f(x)最小,
当x=8时,f(x)最大,
故sin=-1,且sin=1.
又因为0<|φ|<π,故φ=-.
所以入住客栈的游客人数与月份之间的关系式为
f(x)=200sin+300.
(2)由条件可知,200sin+300≥400,化简得
sin≥?2kπ+≤x-≤2kπ+,k∈Z,
解得12k+6≤x≤12k+10,k∈Z.
因为x∈N*,且1≤x≤12,所以x=6,7,8,9,10.
即只有6,7,8,9,10五个月份要准备400份以上的食物.
13.(选做题)下表是某地某年月平均气温(华氏):
月份
1
2
3
4
5
6
平均气温
21.4
26.0
36.0
48.8
59.1
68.6
月份
7
8
9
10
11
12
平均气温
73.0
71.9
64.7
53.5
39.8
27.7
以月份为x轴(x=月份-1),以平均气温为y轴.
(1)用正弦曲线去拟合这些数据;
(2)估计这个正弦曲线的周期T和振幅A;
(3)下面三个函数模型中,哪一个最适合这些数据?
①=cos;②=cos;③=cos.
解 (1)如图.
(2)最低气温为1月份21.4,最高气温为7月份73.0,
故=7-1=6,所以T=12.
因为2A的值等于最高气温与最低气温的差,
即2A=73.0-21.4=51.6,所以A=25.8.
(3)因为x=月份-1,
所以不妨取x=2-1=1,y=26.0.
代入①,得=>1≠cos,故①不适合;代入②,得=<0≠cos,故②不适合.所以应选③.
