第1章 三角函数章末复习课学案
文档属性
| 名称 | 第1章 三角函数章末复习课学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 352.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-16 00:00:00 | ||
图片预览




文档简介
章末复习课
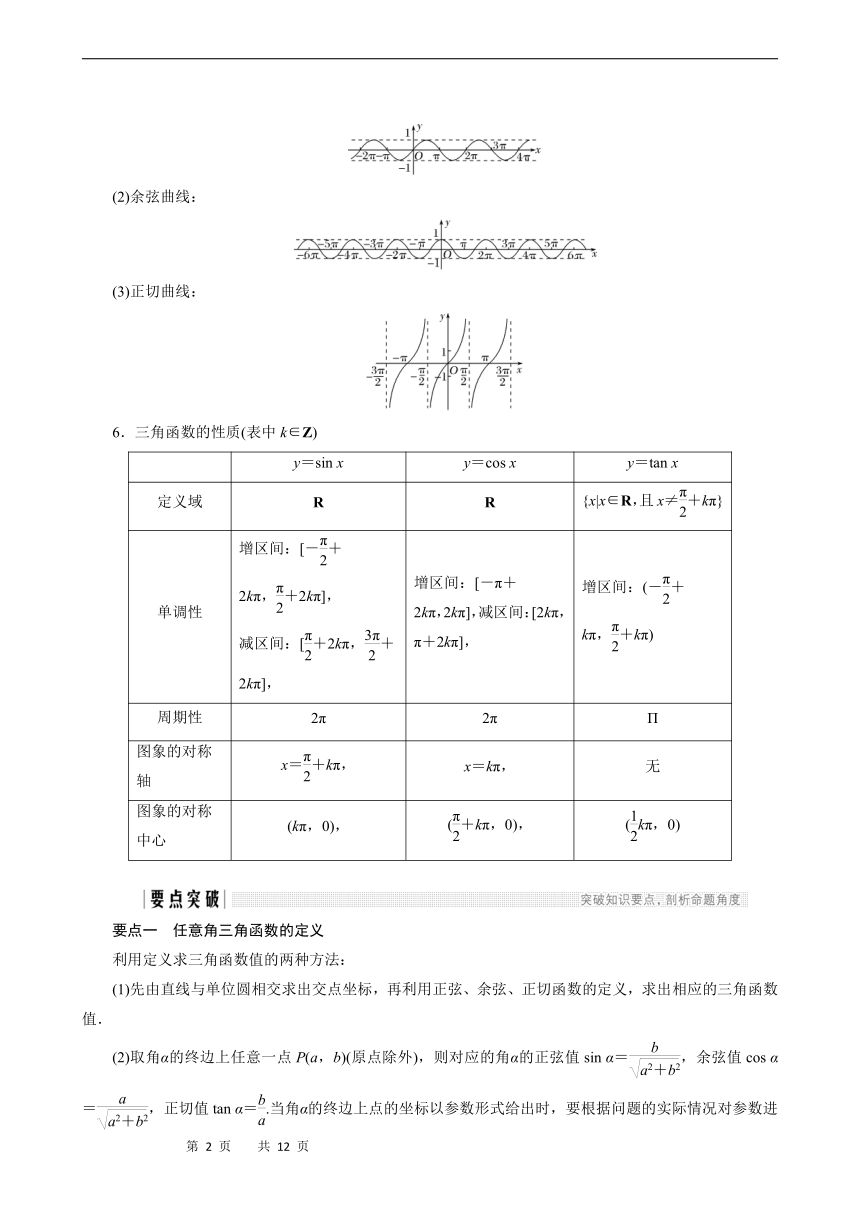
网络构建
核心归纳
1.任意角与弧度制
(1)与角α终边相同的角的集合为S={β|β=α+2kπ,k∈Z}.
(2)角度与弧度的互化:1°= rad,1 rad=()°.
(3)弧长公式:l=|α|r,
扇形面积公式:S=l r=|α|r2.
2.任意角的三角函数
设任意角α的终边上任意一点P(x,y),则sin α=,cos α=,tan α=(x≠0).
3.同角三角函数基本关系式:sin2α+cos2α=1;=tan α.
4.诱导公式
(1)记忆口诀:奇变偶不变,符号看象限.
(2)功能:将k·±α(k∈Z)的三角函数值化为α的三角函数值,实现变名、变号或变角等作用.
5.三角函数的图象
(1)正弦曲线:
(2)余弦曲线:
(3)正切曲线:
6.三角函数的性质(表中k∈Z)
y=sin x
y=cos x
y=tan x
定义域
R
R
{x|x∈R,且x≠+kπ}
单调性
增区间:[-+
2kπ,+2kπ],
减区间:[+2kπ,+2kπ],
增区间:[-π+
2kπ,2kπ],减区间:[2kπ,π+2kπ],
增区间:(-+
kπ,+kπ)
周期性
2π
2π
Π
图象的对称轴
x=+kπ,
x=kπ,
无
图象的对称中心
(kπ,0),
(+kπ,0),
(kπ,0)
要点一 任意角三角函数的定义
利用定义求三角函数值的两种方法:
(1)先由直线与单位圆相交求出交点坐标,再利用正弦、余弦、正切函数的定义,求出相应的三角函数值.
(2)取角α的终边上任意一点P(a,b)(原点除外),则对应的角α的正弦值sin α=,余弦值cos α=,正切值tan α=.当角α的终边上点的坐标以参数形式给出时,要根据问题的实际情况对参数进行分类讨论.
【例1】 已知角α的终边经过点P(3m-9,m+2).
(1)若m=2,求5sin α+3tan α的值;
(2)若cos α≤0,且sin α>0,求实数m的取值范围.
解 (1)若m=2,则P(-3,4),
所以x=-3,y=4,r=5,
所以sin α=,cos α=-,tan α=-,
故5sin α+3tan α=5×+3×(-)=4-4=0.
(2)由题意知,cos α=≤0,sin α=>0,
即x≤0,y>0,
所以所以-2【训练1】 已知角θ的终边经过点P(-,m) (m≠0)且sin θ=m,试判断角θ所在的象限,并求cos θ和tan θ的值.
解 由题意,得r=,
所以sin θ==m.
因为m≠0,所以m=±,故角θ是第二或第三象限角.
当m=时,r=2,点P的坐标为(-,),角θ是第二象限角,
所以cos θ===-,
tan θ===-;
当m=-时,r=2,点P的坐标为(-,-),角θ是第三象限角,所以cos θ===-,
tan θ===.
典例
迁移
要点二 同角三角函数基本关系式的应用
同角三角函数基本关系式的应用方法
(1)利用sin2α+cos2α=1可以实现α的正弦、余弦的转化,利用=tan α可以实现角α弦切互化.
(2)关系式的逆用与变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α,
(sin α+cos α)2=(sin α-cos α)2+4sin αcos α.
(3)sin α,cos α的齐次式的应用:分式中分子与分母是关于sin α,cos α的齐次式或含有sin2α,cos2α及sin αcos α的式子求值时,可将所求式子的分母看作“1”,利用“sin2α+cos2α=1”代换后转化为“切”求解.
【例2】 (1)已知tan α=,α∈(0,),则sin α-cos α=________;
解析 因为tan α==,
由
解得sin α=,cos α=,
所以sin α-cos α=-=-.
答案 -
(2)已知α是三角形的内角,且sin α+cos α=.
①求tan α的值;
②把用tan α表示出来,并求其值.
解 ①由sin α+cos α=,
得1+2sin αcos α=,
所以sin αcos α=-,
因为α是三角形的内角,所以sin α>0,cos α<0,
∴sin α-cos α=
=
==,
故得sin α=,cos α=-,tan α=-.
②==,
又tan α=-,
所以==-.
【迁移】 本例(2)中保持条件不变,求:
(1);(2)sin2α+2sin αcos α.
解 (1)原式===.
(2)原式====-.
要点三 诱导公式的应用
用诱导公式化简求值的方法
(1)对于三角函数式的化简求值,关键在于根据给出角的特点,将角化成2kπ±α,π±α,±α,π±α(或k·±α,k∈Z)的形式,再用“奇变偶不变,符号看象限”来化简.
(2)解决“已知某个三角函数值,求其他三角函数值”的问题,关键在于观察分析条件角与结论角,清除条件与结论之间的差异,将已知和未知联系起来,还应注意整体思想的应用.
【例3】 (1)已知cos=,求cos的值;
解 ∵+=π,
∴-α=π-.
∴cos=cos
=-cos=-,
即cos=-.
(2)已知π<α<2π,cos(α-7π)=-,求sin(3π+α)·tan的值.
解 ∵cos(α-7π)=cos(7π-α)
=cos(π-α)=-cos α=-,
∴cos α=.
∴sin(3π+α)·tan
=sin(π+α)·
=sin α·tan
=sin α·
=sin α·
=cos α=.
【训练2】 (1)已知sin=,则cos的值为________;
解析 cos=cos
=-sin=-.
答案 -
(2)已知sin α是方程2x2-x-1=0的根,α是第三象限角,则·tan2(π-α)=________.
解析 ∵方程2x2-x-1=0的根为-或1,
又α是第三象限角,∴sin α=-,
∴cos α=-=-,
∴tan α==,
∴原式=·tan2α=-tan2α=.
答案
要点四 三角函数的图象
1.用“五点法”作函数y=Asin(ωx+φ)图象的步骤:
第一步:列表,由ωx+φ=0,,π,,2π先求出x,再由ωx+φ的值求出y的值.
X
-
-
-
-
-
ωx+φ
0
π
π
2π
Y
0
A
0
-A
0
第二步:在同一坐标系中描出各点.
第三步:用光滑曲线连接这些点,进而成图象.
2.由图象或部分图象确定解析式y=Asin(ωx+φ)中的参数
(1)A:由最大值、最小值来确定A.
(2)ω:通过求周期T来确定ω.
(3)φ:利用已知点列方程求出.
【例4】 (1)下图所示是函数y=Asin(ωx+φ)(A>0,ω>0)图象的一部分,则其函数解析式是( )
A.y=sin B.y=sin
C.y=sin D.y=sin
解析 由题图可知A=1,=-=,∴T=2π,ω==1,又1×+φ=0,即φ=,故y=sin.
答案 A
(2)已知f(x)=1+sin(2x-),画出f(x)在x∈[-,]上的图象.
解 (1)∵x∈,
∴2x-∈.
列表:
X
-
-
-
2x-
-
-π
-
0
f(x)
2
1
1-
1
1+
2
(2)描点,连线,如图所示.
【训练3】 函数f(x)=2sin(ωx+φ)的部分图象如右图所示,则ω,φ的值分别是________.
解析 由题图可知=-,
∴T=π,ω==2,又2×+φ=,所以φ=-.
答案 2,-
要点五 三角函数图象的变换
由函数y=sin x的图象通过变换得到函数y=Asin(ωx+φ)的图象的两种方法
【例5】 如图是函数y=Asin(ωx+φ)(A>0,ω>0,x∈R)在区间上的图象.为了得到这个函数的图象,只要将y=sin x(x∈R)的图象上所有的点( )
A.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变
B.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
C.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变
D.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
解析 由题图象知A=1,T=-=π,所以ω==2.所以f(x)=sin(2x+φ),又图象过点,由五点法知+φ=π,所以φ=,所以y=sin.
故将函数y=sin x的图象先向左平移个单位后,再把所得图象上各点的横坐标缩短为原来的(纵坐标不变),可得函数y=sin的图象.
答案 A
【训练4】 将函数y=cos的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向左平移个单位,所得函数图象的一条对称轴是( )
A.x= B.x=
C.x=π D.x=
解析 y=cos
y=cos
y=cos,即y=cos.
由余弦函数的性质可知,其对称轴一定经过图象的最高点或最低点,又当x=时,y=cos=1,故选D.
答案 D
考查
方向
要点六 三角函数的性质
1.三角函数的两条性质
(1)周期性:函数y=Asin(ωx+φ)和y=Acos(ωx+φ)的最小正周期为,y=tan(ωx+φ)的最小正周期为.
(2)奇偶性:三角函数中奇函数一般可化为y=Asin ωx或y=Atan ωx,而偶函数一般可化为y=Acos ωx+B的形式.
2.求三角函数值域(最值)的方法
(1)利用sin x,cos x的有界性.
(2)从y=Asin(ωx+φ)+k的形式逐步分析ωx+φ的范围,根据正弦函数单调性写出函数的值域.
(3)换元法:把sin x或cos x看作一个整体,可化为求函数在区间上的值域(最值)问题.
特别提醒:利用换元法求三角函数的值域时,一定要注意三角函数自身的取值范围,否则会出现错误.
3.求三角函数的单调区间
求形如y=Asin(ωx+φ)或y=Acos(ωx+φ)(A>0,ω>0)的函数的单调区间可以通过解不等式方法去解答,即把ωx+φ视为一个“整体”,分别与正弦函数y=sin x,余弦函数y=cos x的单调递增(减)区间对应解出x,即得所求的单调递增(减)区间.
方向1 三角函数的周期性和奇偶性
【例6-1】 已知函数f(x)=sin-1,下列命题正确的是( )
A.f(x)是周期为1的奇函数
B.f(x)是周期为2的偶函数
C.f(x)是周期为1的非奇非偶函数
D.f(x)是周期为2的非奇非偶函数
解析 f(x)=sin(πx-)-1=-sin(-πx)-1=-cos πx-1,
∴f(-x)=-cos(-πx)-1=-cos πx-1=f(x),则函数f(x)是偶函数,且周期为T==2.
答案 B
方向2 三角函数的单调性
【例6-2】 已知函数f(x)=-2sin(2x+φ)(|φ|<π),若f()=-2,则f(x)的一个单调递减区间是( )
A.[-,] B.[,]
C.[-,] D.[,]
解析 由f()=-2得
f()=-2sin(2×+φ)
=-2sin(+φ)=-2,
所以sin(+φ)=1.
因为|φ|<π,所以φ=.
由2kπ-≤2x+≤2kπ+,k∈Z,
解得kπ-≤x≤kπ+,k∈Z.
当k=0时,-≤x≤,故选C.
答案 C
方向3 三角函数性质的综合应用
【例6-3】 已知函数f(x)=2sin+a,a为常数.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调递增区间;
(3)若x∈时,f(x)的最小值为-2,求a的值.
解 (1)f(x)=2sin+a,
所以f(x)的最小正周期T==π.
(2)由2kπ-≤2x-≤2kπ+(k∈Z),
得kπ-≤x≤kπ+(k∈Z),
所以f(x)的单调递增区间为(k∈Z).
(3)当x∈时,2x-∈,
所以x=0时,f(x)取得最小值,
即2sin+a=-2,
故a=-1.
网络构建
核心归纳
1.任意角与弧度制
(1)与角α终边相同的角的集合为S={β|β=α+2kπ,k∈Z}.
(2)角度与弧度的互化:1°= rad,1 rad=()°.
(3)弧长公式:l=|α|r,
扇形面积公式:S=l r=|α|r2.
2.任意角的三角函数
设任意角α的终边上任意一点P(x,y),则sin α=,cos α=,tan α=(x≠0).
3.同角三角函数基本关系式:sin2α+cos2α=1;=tan α.
4.诱导公式
(1)记忆口诀:奇变偶不变,符号看象限.
(2)功能:将k·±α(k∈Z)的三角函数值化为α的三角函数值,实现变名、变号或变角等作用.
5.三角函数的图象
(1)正弦曲线:
(2)余弦曲线:
(3)正切曲线:
6.三角函数的性质(表中k∈Z)
y=sin x
y=cos x
y=tan x
定义域
R
R
{x|x∈R,且x≠+kπ}
单调性
增区间:[-+
2kπ,+2kπ],
减区间:[+2kπ,+2kπ],
增区间:[-π+
2kπ,2kπ],减区间:[2kπ,π+2kπ],
增区间:(-+
kπ,+kπ)
周期性
2π
2π
Π
图象的对称轴
x=+kπ,
x=kπ,
无
图象的对称中心
(kπ,0),
(+kπ,0),
(kπ,0)
要点一 任意角三角函数的定义
利用定义求三角函数值的两种方法:
(1)先由直线与单位圆相交求出交点坐标,再利用正弦、余弦、正切函数的定义,求出相应的三角函数值.
(2)取角α的终边上任意一点P(a,b)(原点除外),则对应的角α的正弦值sin α=,余弦值cos α=,正切值tan α=.当角α的终边上点的坐标以参数形式给出时,要根据问题的实际情况对参数进行分类讨论.
【例1】 已知角α的终边经过点P(3m-9,m+2).
(1)若m=2,求5sin α+3tan α的值;
(2)若cos α≤0,且sin α>0,求实数m的取值范围.
解 (1)若m=2,则P(-3,4),
所以x=-3,y=4,r=5,
所以sin α=,cos α=-,tan α=-,
故5sin α+3tan α=5×+3×(-)=4-4=0.
(2)由题意知,cos α=≤0,sin α=>0,
即x≤0,y>0,
所以所以-2
解 由题意,得r=,
所以sin θ==m.
因为m≠0,所以m=±,故角θ是第二或第三象限角.
当m=时,r=2,点P的坐标为(-,),角θ是第二象限角,
所以cos θ===-,
tan θ===-;
当m=-时,r=2,点P的坐标为(-,-),角θ是第三象限角,所以cos θ===-,
tan θ===.
典例
迁移
要点二 同角三角函数基本关系式的应用
同角三角函数基本关系式的应用方法
(1)利用sin2α+cos2α=1可以实现α的正弦、余弦的转化,利用=tan α可以实现角α弦切互化.
(2)关系式的逆用与变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α,
(sin α+cos α)2=(sin α-cos α)2+4sin αcos α.
(3)sin α,cos α的齐次式的应用:分式中分子与分母是关于sin α,cos α的齐次式或含有sin2α,cos2α及sin αcos α的式子求值时,可将所求式子的分母看作“1”,利用“sin2α+cos2α=1”代换后转化为“切”求解.
【例2】 (1)已知tan α=,α∈(0,),则sin α-cos α=________;
解析 因为tan α==,
由
解得sin α=,cos α=,
所以sin α-cos α=-=-.
答案 -
(2)已知α是三角形的内角,且sin α+cos α=.
①求tan α的值;
②把用tan α表示出来,并求其值.
解 ①由sin α+cos α=,
得1+2sin αcos α=,
所以sin αcos α=-,
因为α是三角形的内角,所以sin α>0,cos α<0,
∴sin α-cos α=
=
==,
故得sin α=,cos α=-,tan α=-.
②==,
又tan α=-,
所以==-.
【迁移】 本例(2)中保持条件不变,求:
(1);(2)sin2α+2sin αcos α.
解 (1)原式===.
(2)原式====-.
要点三 诱导公式的应用
用诱导公式化简求值的方法
(1)对于三角函数式的化简求值,关键在于根据给出角的特点,将角化成2kπ±α,π±α,±α,π±α(或k·±α,k∈Z)的形式,再用“奇变偶不变,符号看象限”来化简.
(2)解决“已知某个三角函数值,求其他三角函数值”的问题,关键在于观察分析条件角与结论角,清除条件与结论之间的差异,将已知和未知联系起来,还应注意整体思想的应用.
【例3】 (1)已知cos=,求cos的值;
解 ∵+=π,
∴-α=π-.
∴cos=cos
=-cos=-,
即cos=-.
(2)已知π<α<2π,cos(α-7π)=-,求sin(3π+α)·tan的值.
解 ∵cos(α-7π)=cos(7π-α)
=cos(π-α)=-cos α=-,
∴cos α=.
∴sin(3π+α)·tan
=sin(π+α)·
=sin α·tan
=sin α·
=sin α·
=cos α=.
【训练2】 (1)已知sin=,则cos的值为________;
解析 cos=cos
=-sin=-.
答案 -
(2)已知sin α是方程2x2-x-1=0的根,α是第三象限角,则·tan2(π-α)=________.
解析 ∵方程2x2-x-1=0的根为-或1,
又α是第三象限角,∴sin α=-,
∴cos α=-=-,
∴tan α==,
∴原式=·tan2α=-tan2α=.
答案
要点四 三角函数的图象
1.用“五点法”作函数y=Asin(ωx+φ)图象的步骤:
第一步:列表,由ωx+φ=0,,π,,2π先求出x,再由ωx+φ的值求出y的值.
X
-
-
-
-
-
ωx+φ
0
π
π
2π
Y
0
A
0
-A
0
第二步:在同一坐标系中描出各点.
第三步:用光滑曲线连接这些点,进而成图象.
2.由图象或部分图象确定解析式y=Asin(ωx+φ)中的参数
(1)A:由最大值、最小值来确定A.
(2)ω:通过求周期T来确定ω.
(3)φ:利用已知点列方程求出.
【例4】 (1)下图所示是函数y=Asin(ωx+φ)(A>0,ω>0)图象的一部分,则其函数解析式是( )
A.y=sin B.y=sin
C.y=sin D.y=sin
解析 由题图可知A=1,=-=,∴T=2π,ω==1,又1×+φ=0,即φ=,故y=sin.
答案 A
(2)已知f(x)=1+sin(2x-),画出f(x)在x∈[-,]上的图象.
解 (1)∵x∈,
∴2x-∈.
列表:
X
-
-
-
2x-
-
-π
-
0
f(x)
2
1
1-
1
1+
2
(2)描点,连线,如图所示.
【训练3】 函数f(x)=2sin(ωx+φ)的部分图象如右图所示,则ω,φ的值分别是________.
解析 由题图可知=-,
∴T=π,ω==2,又2×+φ=,所以φ=-.
答案 2,-
要点五 三角函数图象的变换
由函数y=sin x的图象通过变换得到函数y=Asin(ωx+φ)的图象的两种方法
【例5】 如图是函数y=Asin(ωx+φ)(A>0,ω>0,x∈R)在区间上的图象.为了得到这个函数的图象,只要将y=sin x(x∈R)的图象上所有的点( )
A.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变
B.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
C.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变
D.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
解析 由题图象知A=1,T=-=π,所以ω==2.所以f(x)=sin(2x+φ),又图象过点,由五点法知+φ=π,所以φ=,所以y=sin.
故将函数y=sin x的图象先向左平移个单位后,再把所得图象上各点的横坐标缩短为原来的(纵坐标不变),可得函数y=sin的图象.
答案 A
【训练4】 将函数y=cos的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向左平移个单位,所得函数图象的一条对称轴是( )
A.x= B.x=
C.x=π D.x=
解析 y=cos
y=cos
y=cos,即y=cos.
由余弦函数的性质可知,其对称轴一定经过图象的最高点或最低点,又当x=时,y=cos=1,故选D.
答案 D
考查
方向
要点六 三角函数的性质
1.三角函数的两条性质
(1)周期性:函数y=Asin(ωx+φ)和y=Acos(ωx+φ)的最小正周期为,y=tan(ωx+φ)的最小正周期为.
(2)奇偶性:三角函数中奇函数一般可化为y=Asin ωx或y=Atan ωx,而偶函数一般可化为y=Acos ωx+B的形式.
2.求三角函数值域(最值)的方法
(1)利用sin x,cos x的有界性.
(2)从y=Asin(ωx+φ)+k的形式逐步分析ωx+φ的范围,根据正弦函数单调性写出函数的值域.
(3)换元法:把sin x或cos x看作一个整体,可化为求函数在区间上的值域(最值)问题.
特别提醒:利用换元法求三角函数的值域时,一定要注意三角函数自身的取值范围,否则会出现错误.
3.求三角函数的单调区间
求形如y=Asin(ωx+φ)或y=Acos(ωx+φ)(A>0,ω>0)的函数的单调区间可以通过解不等式方法去解答,即把ωx+φ视为一个“整体”,分别与正弦函数y=sin x,余弦函数y=cos x的单调递增(减)区间对应解出x,即得所求的单调递增(减)区间.
方向1 三角函数的周期性和奇偶性
【例6-1】 已知函数f(x)=sin-1,下列命题正确的是( )
A.f(x)是周期为1的奇函数
B.f(x)是周期为2的偶函数
C.f(x)是周期为1的非奇非偶函数
D.f(x)是周期为2的非奇非偶函数
解析 f(x)=sin(πx-)-1=-sin(-πx)-1=-cos πx-1,
∴f(-x)=-cos(-πx)-1=-cos πx-1=f(x),则函数f(x)是偶函数,且周期为T==2.
答案 B
方向2 三角函数的单调性
【例6-2】 已知函数f(x)=-2sin(2x+φ)(|φ|<π),若f()=-2,则f(x)的一个单调递减区间是( )
A.[-,] B.[,]
C.[-,] D.[,]
解析 由f()=-2得
f()=-2sin(2×+φ)
=-2sin(+φ)=-2,
所以sin(+φ)=1.
因为|φ|<π,所以φ=.
由2kπ-≤2x+≤2kπ+,k∈Z,
解得kπ-≤x≤kπ+,k∈Z.
当k=0时,-≤x≤,故选C.
答案 C
方向3 三角函数性质的综合应用
【例6-3】 已知函数f(x)=2sin+a,a为常数.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调递增区间;
(3)若x∈时,f(x)的最小值为-2,求a的值.
解 (1)f(x)=2sin+a,
所以f(x)的最小正周期T==π.
(2)由2kπ-≤2x-≤2kπ+(k∈Z),
得kπ-≤x≤kπ+(k∈Z),
所以f(x)的单调递增区间为(k∈Z).
(3)当x∈时,2x-∈,
所以x=0时,f(x)取得最小值,
即2sin+a=-2,
故a=-1.
