第四章 几何图形初步全章复习学案(含答案)
文档属性
| 名称 | 第四章 几何图形初步全章复习学案(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-16 16:06:12 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第四章 几何图形初步 全单元学案
知识梳理
1.长方体、圆柱、球、长(正)方形、圆、线段、点等,以及小学学习过的三角形、四边形等,都是从形形色色的物体外形中得出的,它们都是 。
2.有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各个部分不都在同一平面内,它们是 。
3.有些几何图形(如线段、角、三角形、长方形、圆等)的各部分都在同一平面内,它们是 。
4.有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的 。
5.几何体简称 ;包围着体的是 ;面和面相交的地方形成 ;线和线相交的地方是 。
6.经过两点有 条直线,并且只有 条直线,简单说成:
。
7.当两条不同的直线有一个公共点时,我们就称这两条直线 ,这个公共点叫做它们的 。
8.用无刻度的直尺和圆规作图,就是 。
9.两点的所有连线中 最短.简单说成 。
10.连接两点间的线段的长度,叫做这两点的 。
11.1°= ‘ ,1’= " .
12.一般地,从一个角度的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的 。
13.如果两个角的和等于 ,就说这两个角互为余角.如果两个角的和等于
,就说这两个角互为补角。
14.同角(等角)的补角 ;同角(等角)的余角 。
知识反馈
知识点1:立体图形
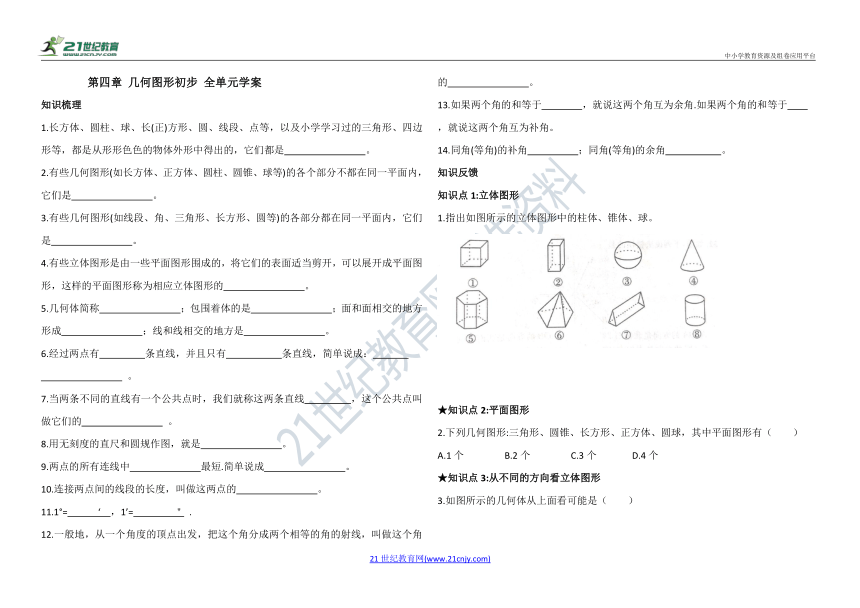
1.指出如图所示的立体图形中的柱体、锥体、球。
★知识点2:平面图形
2.下列几何图形:三角形、圆锥、长方形、正方体、圆球,其中平面图形有( )
A.1个 B.2个 C.3个 D.4个
★知识点3:从不同的方向看立体图形
3.如图所示的几何体从上面看可能是( )
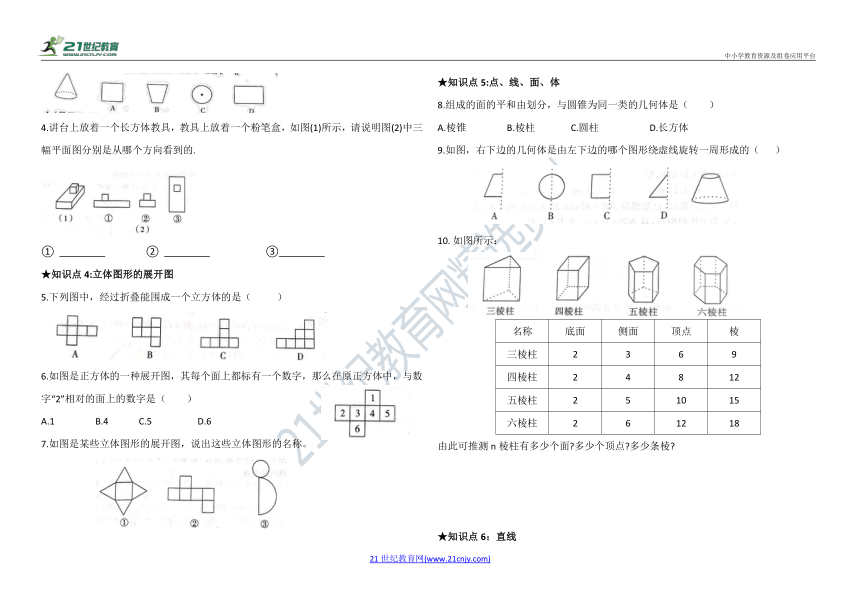
4.讲台上放着一个长方体教具,教具上放着一个粉笔盒,如图(1)所示,请说明图(2)中三幅平面图分别是从哪个方向看到的.
① ② ③
★知识点4:立体图形的展开图
5.下列图中,经过折叠能围成一个立方体的是( )
6.如图是正方体的一种展开图,其每个面上都标有一个数字,那么在原正方体中,与数字“2”相对的面上的数字是( )
A.1 B.4 C.5 D.6
7.如图是某些立体图形的展开图,说出这些立体图形的名称。
★知识点5:点、线、面、体
8.组成的面的平和由划分,与圆锥为同一类的几何体是( )
A.棱锥 B.棱柱 C.圆柱 D.长方体
9.如图,右下边的几何体是由左下边的哪个图形绕虚线旋转一周形成的( )
如图所示:
名称 底面 侧面 顶点 棱
三棱柱 2 3 6 9
四棱柱 2 4 8 12
五棱柱 2 5 10 15
六棱柱 2 6 12 18
由此可推测n棱柱有多少个面?多少个顶点?多少条棱?
★知识点6:直线
11.要想在墙上固定一根木条,至少需要钉钉子( )
A.1个 B.2个 C.3个 D.4个
12.过A、B、C三点作直线,小明说有三条,小颖说有一条,小林说不是一条就是三条,你认为 的说法是正确的.
★知识点7:射线
13.手电筒射出去的光线给我们的形象是( )
A.直线 B.射线 C.线段 D.折线
★知识点8:线段
14.如图,线AB上有C,D两点则图中共有线段( )
A.3条 B.4条 C.5条 D.6条
★知识点9:线段的中点及等分点
15.如图,D、E是AB的三等分点,若DE=2,AC=10,则BC的长为( )
A.2 B.4 C.6 D.8
16.若点C为线段AB的一个三等分点,点D为线段AB的中点,若AB的长为6.6cm,则CD的长为( )
A.0.8 B.1.1 C 3.3 cm D.4.4
16.如图,已知线段AB=80cm,M为AB的中点,P在MB上,N为PB的中点,且NB=14.求PA的长.
知识点10:线段公理及两点间的距离
18.如图,C点在线段AB外,则AC AB+ BC, BC AB+AC, AB AC+BC(填上“<”或“>”),其中的数学道理是 。
19.A,B两点之间的距离是( )
A.连接A,B两点的线段 B.连接A,B两点的直线
C.线段AB的长度 D.直线AB的长度
20.如果点A,B,C在同一条直线上,线段AB=6cm,BC=2cm,则A,C两点的距离为( )
A. 8 cm B.4 C.8cm或4cm D.无法确定
★知识点11:角的定义及表示方法
21.下列说法中正确的是( )
A.由两条射线组成的图形叫做角 B.角的大小与角的两边长有关
C.角的两边是两条射线 D.用放大镜看一个角,角的度数变大了
22.将图中的角用不同的方式表示出来,并填写下表。
∠1 ∠β
∠ACB ∠BAC ∠ABC
★知识点12:角的度量与换算
23.将57.32°用度、分、秒表示的结果是( )
A.58°18'22" B.57°19’12" C. 57°29’22" D.57°39’32"
24.把35°24’36"转化成用度表示的形式.
★知识点13:角的运算及角的平分线
25.如图,已知∠AOB=∠COD=90°,∠BOC=40°,则∠AOD等于( )
A.120° B.100° C.130° D.140°
26.O是直线AB上一点,∠AOC=50°28’,OD平分∠BOC.求∠COD的度数.
27.如图所示,∠AOB是一个平角,射线OE平分∠AOC,射线OF平分∠BOC,求∠EOF的度数.
知识点14:余角、补角的定义及性质
28.已知∠α=70°,则∠α的余角等于 度,若∠α=35°,则∠α的补角是
.
29.因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( )
A.同角的余角相等 B.等角的余角相等
C.同角的补角相等 D.等角的补角相等
30.已知一个角的补角是它的余角的4倍,求这个角的度数。
31.设∠α和∠β分別为(2n-1)°和(68-n)°,且∠α和∠β都是∠θ的补角,∠α与∠β能否互余?为什么?
★知识点15:方位角
32.如图,下列说法错误的是( )
A.OA的方向是北偏西22° B.OB的方向是西南方向
D.OD的方向是北偏东60° C.OC的方向是南偏东60°
参考答案
21世纪教育网(www.21cnjy.com)
第四章 几何图形初步 全单元学案
知识梳理
1.长方体、圆柱、球、长(正)方形、圆、线段、点等,以及小学学习过的三角形、四边形等,都是从形形色色的物体外形中得出的,它们都是 。
2.有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各个部分不都在同一平面内,它们是 。
3.有些几何图形(如线段、角、三角形、长方形、圆等)的各部分都在同一平面内,它们是 。
4.有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的 。
5.几何体简称 ;包围着体的是 ;面和面相交的地方形成 ;线和线相交的地方是 。
6.经过两点有 条直线,并且只有 条直线,简单说成:
。
7.当两条不同的直线有一个公共点时,我们就称这两条直线 ,这个公共点叫做它们的 。
8.用无刻度的直尺和圆规作图,就是 。
9.两点的所有连线中 最短.简单说成 。
10.连接两点间的线段的长度,叫做这两点的 。
11.1°= ‘ ,1’= " .
12.一般地,从一个角度的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的 。
13.如果两个角的和等于 ,就说这两个角互为余角.如果两个角的和等于
,就说这两个角互为补角。
14.同角(等角)的补角 ;同角(等角)的余角 。
知识反馈
知识点1:立体图形
1.指出如图所示的立体图形中的柱体、锥体、球。
★知识点2:平面图形
2.下列几何图形:三角形、圆锥、长方形、正方体、圆球,其中平面图形有( )
A.1个 B.2个 C.3个 D.4个
★知识点3:从不同的方向看立体图形
3.如图所示的几何体从上面看可能是( )
4.讲台上放着一个长方体教具,教具上放着一个粉笔盒,如图(1)所示,请说明图(2)中三幅平面图分别是从哪个方向看到的.
① ② ③
★知识点4:立体图形的展开图
5.下列图中,经过折叠能围成一个立方体的是( )
6.如图是正方体的一种展开图,其每个面上都标有一个数字,那么在原正方体中,与数字“2”相对的面上的数字是( )
A.1 B.4 C.5 D.6
7.如图是某些立体图形的展开图,说出这些立体图形的名称。
★知识点5:点、线、面、体
8.组成的面的平和由划分,与圆锥为同一类的几何体是( )
A.棱锥 B.棱柱 C.圆柱 D.长方体
9.如图,右下边的几何体是由左下边的哪个图形绕虚线旋转一周形成的( )
如图所示:
名称 底面 侧面 顶点 棱
三棱柱 2 3 6 9
四棱柱 2 4 8 12
五棱柱 2 5 10 15
六棱柱 2 6 12 18
由此可推测n棱柱有多少个面?多少个顶点?多少条棱?
★知识点6:直线
11.要想在墙上固定一根木条,至少需要钉钉子( )
A.1个 B.2个 C.3个 D.4个
12.过A、B、C三点作直线,小明说有三条,小颖说有一条,小林说不是一条就是三条,你认为 的说法是正确的.
★知识点7:射线
13.手电筒射出去的光线给我们的形象是( )
A.直线 B.射线 C.线段 D.折线
★知识点8:线段
14.如图,线AB上有C,D两点则图中共有线段( )
A.3条 B.4条 C.5条 D.6条
★知识点9:线段的中点及等分点
15.如图,D、E是AB的三等分点,若DE=2,AC=10,则BC的长为( )
A.2 B.4 C.6 D.8
16.若点C为线段AB的一个三等分点,点D为线段AB的中点,若AB的长为6.6cm,则CD的长为( )
A.0.8 B.1.1 C 3.3 cm D.4.4
16.如图,已知线段AB=80cm,M为AB的中点,P在MB上,N为PB的中点,且NB=14.求PA的长.
知识点10:线段公理及两点间的距离
18.如图,C点在线段AB外,则AC AB+ BC, BC AB+AC, AB AC+BC(填上“<”或“>”),其中的数学道理是 。
19.A,B两点之间的距离是( )
A.连接A,B两点的线段 B.连接A,B两点的直线
C.线段AB的长度 D.直线AB的长度
20.如果点A,B,C在同一条直线上,线段AB=6cm,BC=2cm,则A,C两点的距离为( )
A. 8 cm B.4 C.8cm或4cm D.无法确定
★知识点11:角的定义及表示方法
21.下列说法中正确的是( )
A.由两条射线组成的图形叫做角 B.角的大小与角的两边长有关
C.角的两边是两条射线 D.用放大镜看一个角,角的度数变大了
22.将图中的角用不同的方式表示出来,并填写下表。
∠1 ∠β
∠ACB ∠BAC ∠ABC
★知识点12:角的度量与换算
23.将57.32°用度、分、秒表示的结果是( )
A.58°18'22" B.57°19’12" C. 57°29’22" D.57°39’32"
24.把35°24’36"转化成用度表示的形式.
★知识点13:角的运算及角的平分线
25.如图,已知∠AOB=∠COD=90°,∠BOC=40°,则∠AOD等于( )
A.120° B.100° C.130° D.140°
26.O是直线AB上一点,∠AOC=50°28’,OD平分∠BOC.求∠COD的度数.
27.如图所示,∠AOB是一个平角,射线OE平分∠AOC,射线OF平分∠BOC,求∠EOF的度数.
知识点14:余角、补角的定义及性质
28.已知∠α=70°,则∠α的余角等于 度,若∠α=35°,则∠α的补角是
.
29.因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( )
A.同角的余角相等 B.等角的余角相等
C.同角的补角相等 D.等角的补角相等
30.已知一个角的补角是它的余角的4倍,求这个角的度数。
31.设∠α和∠β分別为(2n-1)°和(68-n)°,且∠α和∠β都是∠θ的补角,∠α与∠β能否互余?为什么?
★知识点15:方位角
32.如图,下列说法错误的是( )
A.OA的方向是北偏西22° B.OB的方向是西南方向
D.OD的方向是北偏东60° C.OC的方向是南偏东60°
参考答案
21世纪教育网(www.21cnjy.com)
