8.3 解三角形的应用举例(1)学案
图片预览




文档简介
8.3 解三角形的应用举例(一)
[学习目标] 1.能够运用正弦、余弦定理解决与方位角有关的航海问题.2.会利用数学建模的思想,结合解三角形的知识,解决与方位角有关的距离问题.
[知识链接]
在下列各小题的空白处填上正确答案:
(1)如图所示,坡角是指坡面与水平面的夹角.(如图所示)
(2)如上图,坡比是指坡面的铅直高度与水平宽度之比,即i=tan α=(i为坡比,α为坡角).
(3)东南方向:指经过目标的射线是正东和正南的夹角平分线.
[预习导引]
1.方位角
从指正北方向线按顺时针方向旋转到目标方向线所成的水平角,叫做方位角.
2.方向角
指北或指南的方向线与目标线所成的小于90°的水平角,叫做方向角,它是方位角的另一种表示形式.
要点一 正弦、余弦定理在航海中的应用
例1 如图,在海岸A处发现北偏东45°方向,距A处(-1)海里的B处有一艘走私船.在A处北偏西75°方向,距A处2海里的C处的我方缉私船奉命以10海里/时的速度追截走私船,此时走私船正以10海里/时的速度,从B处向北偏东30°方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
解 设缉私船应沿CD方向行驶t小时,才能最快截获(在D点)走私船,
则CD=10t海里,BD=10t海里,在△ABC中,
由余弦定理,有BC2=AB2+AC2-2AB·ACcosA
=(-1)2+22-2(-1)·2·cos120°=6.
∴BC=海里.又∵=,
∴sin∠ABC===,
∴∠ABC=45°,∴B点在C点的正东方向上,
∴∠CBD=90°+30°=120°,
在△BCD中,由正弦定理,得=,
∴sin∠BCD===.
∴∠BCD=30°,∴缉私船沿北偏东60°的方向行驶.又在△BCD中,∠CBD=120°,∠BCD=30°,
∴∠D=30°,∴BD=BC,即10t=.
∴t=小时≈15分钟.
∴缉私船应沿北偏东60°的方向行驶,才能最快截获走私船,大约需要15分钟.
规律方法 航海问题是解三角形应用问题中的一类很重要的问题,解决这类问题一定要搞清方位角,再就是选择好不动点,然后根据条件,画出示意图,转化为三角形问题.
跟踪演练1 甲船在A点发现乙船在北偏东60°的B处,乙船以每小时a海里的速度向北行驶,已知甲船的速度是每小时a海里,问甲船应沿着什么方向前进,才能最快与乙船相遇?
解 如图所示.设经过t小时两船在C点相遇,则
在△ABC中,BC=at海里,AC=at海里,
B=90°+30°=120°,由=得:
sin∠CAB====.
∵0°<∠CAB<90°,∴∠CAB=30°.
∴∠DAC=60°-30°=30°.
所以甲船应沿着北偏东30°的方向前进,才能最快与乙船相遇.
要点二 正弦、余弦定理在测量距离中的应用
例2 某观测站C在目标A的南偏西25°方向,从A出发有一条南偏东35°走向的公路,在C处测得与C相距31千米的公路上的B处有一人正沿此公路向A走去,走20千米到达D,此时测得CD为21千米,求此人在D处距A还有多少千米?
解 如图所示,易知∠CAD=25°+35°=60°,在△BCD中,
cosB==,所以sinB=.
在△ABC中,AC===24(千米).
由BC2=AC2+AB2-2AC·AB·cos∠CAB
得AB2-24AB-385=0,解得AB=35或AB=-11(舍去).
∴AD=AB-BD=15(千米).
∴故此人在D处距A还有15千米.
规律方法 由问题中的有关量提炼出三角形中的元素,用正弦、余弦定理解三角形.
跟踪演练2 已知A船在灯塔C北偏东80°方向,且A船到灯塔C的距离为2km,B船在灯塔C北偏西40°方向,A、B两船间的距离为3km,则B船到灯塔C的距离为______km.
答案 -1
解析 如图,由题意可得∠ACB=120°,AC=2,AB=3.设BC=x,
则由余弦定理可得:
AB2=BC2+AC2-2BC·ACcos120°,
即32=22+x2-2×2xcos120°,整理得x2+2x=5,
解得x=-1.
1.已知两座灯塔A,B与海洋观测站C的距离相等,灯塔A在观测站C的北偏东40°,灯塔B在观测站C的南偏东60°,则灯塔A在灯塔B的( )
A.北偏东10° B.北偏西10°
C.南偏东10° D.南偏西10°
答案 B
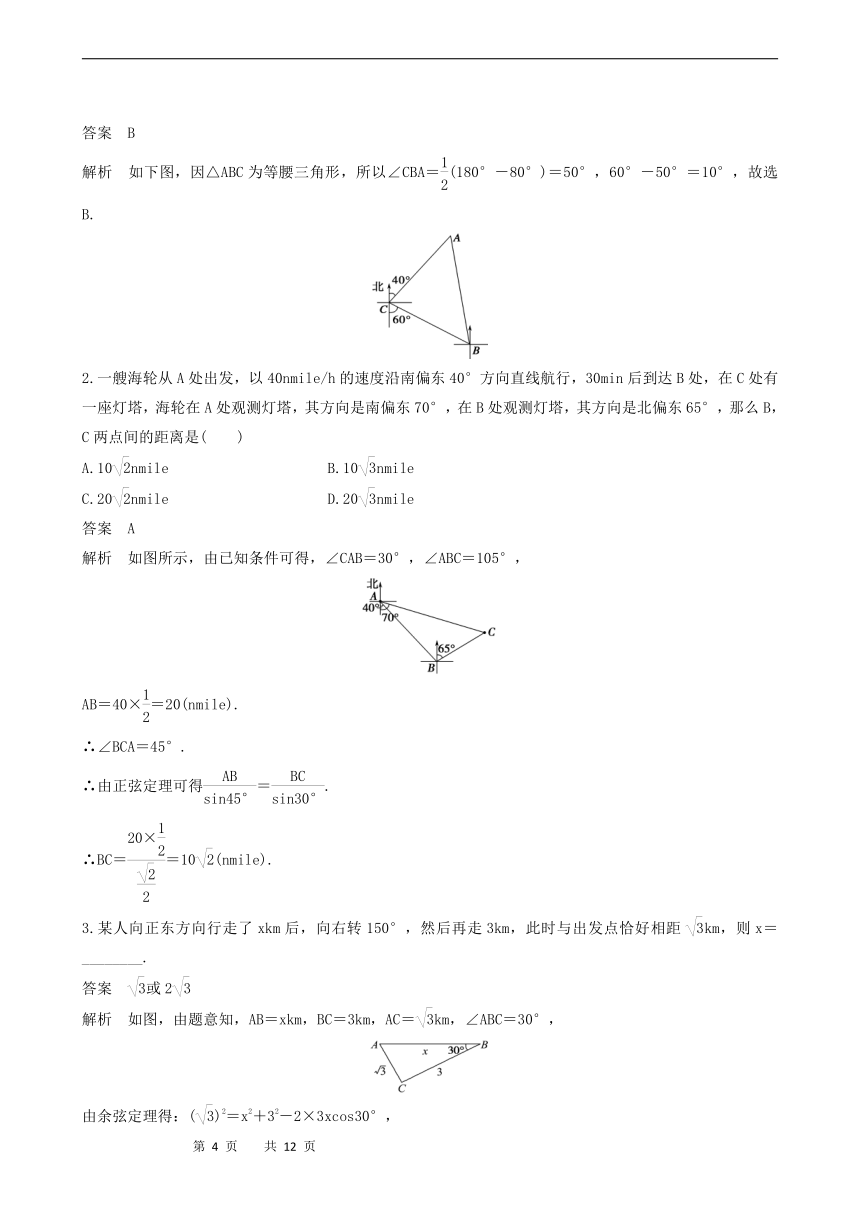
解析 如下图,因△ABC为等腰三角形,所以∠CBA=(180°-80°)=50°,60°-50°=10°,故选B.
2.一艘海轮从A处出发,以40nmile/h的速度沿南偏东40°方向直线航行,30min后到达B处,在C处有一座灯塔,海轮在A处观测灯塔,其方向是南偏东70°,在B处观测灯塔,其方向是北偏东65°,那么B,C两点间的距离是( )
A.10nmile B.10nmile
C.20nmile D.20nmile
答案 A
解析 如图所示,由已知条件可得,∠CAB=30°,∠ABC=105°,
AB=40×=20(nmile).
∴∠BCA=45°.
∴由正弦定理可得=.
∴BC==10(nmile).
3.某人向正东方向行走了xkm后,向右转150°,然后再走3km,此时与出发点恰好相距km,则x=________.
答案 或2
解析 如图,由题意知,AB=xkm,BC=3km,AC=km,∠ABC=30°,
由余弦定理得:()2=x2+32-2×3xcos30°,
即x2-3x+6=0,解得x=或x=2.
4.如图,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°相距20海里的C处的乙船,现乙船朝北偏东θ的方向沿直线CB前往B处救援,求cosθ的值.
解 在△ABC中,AB=40,AC=20,∠BAC=120°,
由余弦定理,得BC2=AB2+AC2-2AB·AC·cos120°=2800,∴BC=20
由正弦定理=,
sin∠ACB=sin∠BAC=.
∵∠BAC=120°,则∠ACB为锐角,cos∠ACB=.
∴cosθ=cos(∠ACB+30°)
=cos∠ACBcos30°-sin∠ACBsin30°
=×-×=.
1.在解三角形时,我们可以根据正弦函数的定义得到两个解,但作为有关现实生活的应用题,必须检验上述所求的解是否符合实际意义,从而得出实际问题的解.
2.解三角形的应用题时,通常会遇到两种情况:
(1)已知量与未知量全部集中在一个三角形中,依次利用正弦定理或余弦定理解之.
(2)已知量与未知量涉及两个或几个三角形,这时需要选择条件足够的三角形优先研究,再逐步在其余的三角形中求出问题的解.
一、基础达标
1.海上有A、B两个小岛相距10nmile,从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,则B、C间的距离是( )
A.10nmile B.nmile
C.5nmile D.5nmile
答案 D
解析 由题意知,在△ABC中AB=10,A=60°,B=75°,则C=180°-A-B=45°.
由正弦定理,得BC===5(nmile).
2.如图,一客轮以速率2v由A至B再到C匀速航行,一货船从AC的中点D出发,以速率v沿直线匀速航行,将货物送达客轮,已知AB⊥BC,AB=BC=50海里,若两船同时出发,则两船相遇之处M距C点的距离为( )
A.海里 B.海里
C.25海里 D.10海里
答案 A
解析 由题意知,M在BC上,设DM=x,则CM=100-2x,
在△CDM中,由余弦定理得:
x2=(25)2+(100-2x)2-2×25(100-2x)·cos45°,
解得x=50-,∴CM=.
3.从高出海平面h米的小岛看正东方向有一只船俯角为30°,看正南方向有一只船俯角为45°,则此时两船间的距离为( )
A.2h米B.h米C.h米D.2h米
答案 A
解析 如图所示,BC=h,AC=h,
∴AB==2h (米).
4.甲骑电动自行车以24km/h的速度沿着正北方向的公路行驶,在点A处望见电视塔S在电动车的北偏东30°方向上,15min后到点B处望见电视塔在电动车的北偏东75°方向上,则电动车在点B时与电视塔S的距离是( )
A.6kmB.3kmC.3kmD.3km
答案 C
解析 由题意知,AB=24×=6(km),∠BAS=30°,
∠ASB=75°-30°=45°.
由正弦定理,得
BS===3(km).
5.某货轮在A处看灯塔B在货轮北偏东75°,距离为12nmile;在A处看灯塔C在货轮的北偏西30°,距离为8nmile.货轮由A处向正北航行到D处时,再看灯塔B在南偏东60°,则A处与D处之间的距离为________nmile;灯塔C与D处之间的距离为________nmile.
答案 24 8
解析 (1)在△ABD中,由已知得∠ADB=60°,
∠B=45°;
由正弦定理得AD===24;
(2)在△ADC中,由余弦定理得CD2=AD2+AC2-2AD·ACcos30°,解得CD=8.
所以A处与D处之间的距离为24nmile,灯塔C与D处之间的距离为8nmile.
6.甲船在A处观察到乙船在它的北偏东60°方向的B处,两船相距anmile,乙船向正北方向行驶.若甲船的速度是乙船速度的倍,问甲船应沿什么方向前进才能最快追上乙船?相遇时乙船行驶多少nmile?
解 如图所示,设两船在C处相遇,并设∠CAB=θ,
乙船行驶距离BC为xnmile,
则AC=xnmile,
由正弦定理得sinθ==,而θ<60°,
∴θ=30°,即∠ACB=θ=30°,AB=BC=a,
从而BC==a (nmile).
答 甲船应沿北偏东30°方向前进才能最快追上乙船,两船相遇时乙船行驶了anmile.
7.某渔船在航行中不幸遇险,发出呼叫信号,我海军舰艇在A处获悉后,立即测出该渔船在方位角为45°,距离为10海里的C处,并测得渔船正沿方位角为105°的方向,以10海里/时的速度行驶,我海军舰艇立即以10海里/时的速度前去营救,求舰艇的航向和靠近渔船所需的时间.
解 如图所示,设舰艇与渔船在B处相遇时所用时间为t小时,
则AB=10t,CB=10t,
在△ABC中,根据余弦定理,则有
AB2=AC2+BC2-2AC·BCcos120°,
可得(10t)2=102+(10t)2-2×10×10tcos120°,
整理得2t2-t-1=0,解得t=1或t=-(舍去).
即舰艇需1小时靠近渔船,此时AB=10,BC=10,
在△ABC中,由正弦定理得=,
所以sin∠CAB===,
所以∠CAB=30°,所以舰艇航行的方位角为75°.
二、能力提升
8.台风中心从A地以20km/h的速度向东北方向移动,离台风中心30km内的地区为危险区,城市B在A的正东40km处,B城市处于危险区内的时间为( )
A.0.5hB.1hC.1.5hD.2h
答案 B
解析 设A地东北方向上点P到B的距离为30km,AP=x,在△ABP中,PB2=AP2+AB2-2AP·ABcosA,
即302=x2+402-2x·40cos45°,
化简得x2-40x+700=0.
设该方程的两根为x1,x2,
则|x1-x2|2=(x1+x2)2-4x1x2=400,
|x1-x2|=20,故t===1.故选B.
9.如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=________m.
答案 150
解析 根据图示,AC=100m.
在△MAC中,∠CMA=180°-75°-60°=45°.
由正弦定理得=?AM=100m.
在△AMN中,=sin60°,
∴MN=100×=150(m).
10.一船以每小时15km的速度向东航行,船在A处看到一个灯塔B在北偏东60°,行驶4h后,船到达C处,看到这个灯塔在北偏东15°,这时船与灯塔的距离为______km.
答案 30
解析 如图,由已知条件,
得AC=60km,∠BAC=30°,
∠ACB=105°,∠ABC=45°.
由正弦定理
BC=
=30(km).
11.某海上养殖基地A,接到气象部门预报,位于基地南偏东60°相距20(+1)海里的海面上有一台风中心,影响半径为20海里,正以每小时10海里的速度沿某一方向匀速直线前进,预计台风中心将从基地东北方向刮过且(+1)小时后开始影响基地持续2小时.求台风移动的方向.
解 如图所示,设预报时台风中心为B,开始影响基地时台风中心为C,基地刚好不受影响时台风中心为D,则B,C,D在一直线上,且AD=20,AC=20.
由题意AB=20(+1),DC=20,
BC=(+1)·10.
在△ADC中,∵DC2=AD2+AC2,
∴∠DAC=90°,∠ADC=45°.在△ABC中,
由余弦定理得cos∠BAC==.
∴∠BAC=30°,又∵B位于A南偏东60°,
60°+30°+90°=180°,∴D位于A的正北方向,
又∵∠ADC=45°,
∴台风移动的方向为向量的方向.即北偏西45°方向.
所以台风向北偏西45°方向移动.
12.如图,A,B是海面上位于东西方向相距5(+1)海里的两个观测点.现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20海里的C点的救援船立即前往营救,其航行速度为30海里/时,该救援船到达D点需要多长时间?
解 由题意知∠DBA=90°-60°=30°,∠DAB=90°-45°=45°,
∴∠ADB=180°-(45°+30°)=105°,
在△DAB中,由正弦定理得=,
∴DB===10(海里),
又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,BC=20(海里),
在△DBC中,由余弦定理得
CD2=BD2+BC2-2BD·BCcos∠DBC=300+1200-2×10×20×=900,
∴CD=30(海里),则需要的时间t==1(小时).
答 救援船到达D点需要1小时.
三、探究与创新
13.如图所示,A,B两个小岛相距21海里,B岛在A岛的正南方,现在甲船从A岛出发,以9海里的速度向B岛行驶,而乙船同时以6海里的速度离开B岛向南偏东60°方向行驶,问行驶多少时间后,两船相距最近,并求出两船的最近距离.
解 如图,行驶th后,甲船行驶了9t海里到达C处,乙船行驶了6t海里到达D处.
当9t<21,即t<时,C在线段AB上,此时BC=(21-9t)海里,
在△BCD中,BC=(21-9t)海里,BD=6t海里,
∠CBD=180°-60°=120°,
由余弦定理知CD2=BC2+BD2-2BC·BD·cos120°=(21-9t)2+(6t)2-2(21-9t)·6t·(-)
=63t2-252t+441=63(t-2)2+189.
当t=2时,CD取得最小值=3.
当t=时,C与B重合,
此时CD=6×=14(海里)>3(海里).
当t>时,BC=(9t-21)(海里),
则CD2=(9t-21)2+(6t)2-2×(9t-21)×6t·cos60°
=63t2-252t+441=63(t-2)2+189>189.
综上可知t=2时,CD取得最小值3.
答 行驶2h后,甲、乙两船相距最近为3海里.
[学习目标] 1.能够运用正弦、余弦定理解决与方位角有关的航海问题.2.会利用数学建模的思想,结合解三角形的知识,解决与方位角有关的距离问题.
[知识链接]
在下列各小题的空白处填上正确答案:
(1)如图所示,坡角是指坡面与水平面的夹角.(如图所示)
(2)如上图,坡比是指坡面的铅直高度与水平宽度之比,即i=tan α=(i为坡比,α为坡角).
(3)东南方向:指经过目标的射线是正东和正南的夹角平分线.
[预习导引]
1.方位角
从指正北方向线按顺时针方向旋转到目标方向线所成的水平角,叫做方位角.
2.方向角
指北或指南的方向线与目标线所成的小于90°的水平角,叫做方向角,它是方位角的另一种表示形式.
要点一 正弦、余弦定理在航海中的应用
例1 如图,在海岸A处发现北偏东45°方向,距A处(-1)海里的B处有一艘走私船.在A处北偏西75°方向,距A处2海里的C处的我方缉私船奉命以10海里/时的速度追截走私船,此时走私船正以10海里/时的速度,从B处向北偏东30°方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
解 设缉私船应沿CD方向行驶t小时,才能最快截获(在D点)走私船,
则CD=10t海里,BD=10t海里,在△ABC中,
由余弦定理,有BC2=AB2+AC2-2AB·ACcosA
=(-1)2+22-2(-1)·2·cos120°=6.
∴BC=海里.又∵=,
∴sin∠ABC===,
∴∠ABC=45°,∴B点在C点的正东方向上,
∴∠CBD=90°+30°=120°,
在△BCD中,由正弦定理,得=,
∴sin∠BCD===.
∴∠BCD=30°,∴缉私船沿北偏东60°的方向行驶.又在△BCD中,∠CBD=120°,∠BCD=30°,
∴∠D=30°,∴BD=BC,即10t=.
∴t=小时≈15分钟.
∴缉私船应沿北偏东60°的方向行驶,才能最快截获走私船,大约需要15分钟.
规律方法 航海问题是解三角形应用问题中的一类很重要的问题,解决这类问题一定要搞清方位角,再就是选择好不动点,然后根据条件,画出示意图,转化为三角形问题.
跟踪演练1 甲船在A点发现乙船在北偏东60°的B处,乙船以每小时a海里的速度向北行驶,已知甲船的速度是每小时a海里,问甲船应沿着什么方向前进,才能最快与乙船相遇?
解 如图所示.设经过t小时两船在C点相遇,则
在△ABC中,BC=at海里,AC=at海里,
B=90°+30°=120°,由=得:
sin∠CAB====.
∵0°<∠CAB<90°,∴∠CAB=30°.
∴∠DAC=60°-30°=30°.
所以甲船应沿着北偏东30°的方向前进,才能最快与乙船相遇.
要点二 正弦、余弦定理在测量距离中的应用
例2 某观测站C在目标A的南偏西25°方向,从A出发有一条南偏东35°走向的公路,在C处测得与C相距31千米的公路上的B处有一人正沿此公路向A走去,走20千米到达D,此时测得CD为21千米,求此人在D处距A还有多少千米?
解 如图所示,易知∠CAD=25°+35°=60°,在△BCD中,
cosB==,所以sinB=.
在△ABC中,AC===24(千米).
由BC2=AC2+AB2-2AC·AB·cos∠CAB
得AB2-24AB-385=0,解得AB=35或AB=-11(舍去).
∴AD=AB-BD=15(千米).
∴故此人在D处距A还有15千米.
规律方法 由问题中的有关量提炼出三角形中的元素,用正弦、余弦定理解三角形.
跟踪演练2 已知A船在灯塔C北偏东80°方向,且A船到灯塔C的距离为2km,B船在灯塔C北偏西40°方向,A、B两船间的距离为3km,则B船到灯塔C的距离为______km.
答案 -1
解析 如图,由题意可得∠ACB=120°,AC=2,AB=3.设BC=x,
则由余弦定理可得:
AB2=BC2+AC2-2BC·ACcos120°,
即32=22+x2-2×2xcos120°,整理得x2+2x=5,
解得x=-1.
1.已知两座灯塔A,B与海洋观测站C的距离相等,灯塔A在观测站C的北偏东40°,灯塔B在观测站C的南偏东60°,则灯塔A在灯塔B的( )
A.北偏东10° B.北偏西10°
C.南偏东10° D.南偏西10°
答案 B
解析 如下图,因△ABC为等腰三角形,所以∠CBA=(180°-80°)=50°,60°-50°=10°,故选B.
2.一艘海轮从A处出发,以40nmile/h的速度沿南偏东40°方向直线航行,30min后到达B处,在C处有一座灯塔,海轮在A处观测灯塔,其方向是南偏东70°,在B处观测灯塔,其方向是北偏东65°,那么B,C两点间的距离是( )
A.10nmile B.10nmile
C.20nmile D.20nmile
答案 A
解析 如图所示,由已知条件可得,∠CAB=30°,∠ABC=105°,
AB=40×=20(nmile).
∴∠BCA=45°.
∴由正弦定理可得=.
∴BC==10(nmile).
3.某人向正东方向行走了xkm后,向右转150°,然后再走3km,此时与出发点恰好相距km,则x=________.
答案 或2
解析 如图,由题意知,AB=xkm,BC=3km,AC=km,∠ABC=30°,
由余弦定理得:()2=x2+32-2×3xcos30°,
即x2-3x+6=0,解得x=或x=2.
4.如图,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°相距20海里的C处的乙船,现乙船朝北偏东θ的方向沿直线CB前往B处救援,求cosθ的值.
解 在△ABC中,AB=40,AC=20,∠BAC=120°,
由余弦定理,得BC2=AB2+AC2-2AB·AC·cos120°=2800,∴BC=20
由正弦定理=,
sin∠ACB=sin∠BAC=.
∵∠BAC=120°,则∠ACB为锐角,cos∠ACB=.
∴cosθ=cos(∠ACB+30°)
=cos∠ACBcos30°-sin∠ACBsin30°
=×-×=.
1.在解三角形时,我们可以根据正弦函数的定义得到两个解,但作为有关现实生活的应用题,必须检验上述所求的解是否符合实际意义,从而得出实际问题的解.
2.解三角形的应用题时,通常会遇到两种情况:
(1)已知量与未知量全部集中在一个三角形中,依次利用正弦定理或余弦定理解之.
(2)已知量与未知量涉及两个或几个三角形,这时需要选择条件足够的三角形优先研究,再逐步在其余的三角形中求出问题的解.
一、基础达标
1.海上有A、B两个小岛相距10nmile,从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,则B、C间的距离是( )
A.10nmile B.nmile
C.5nmile D.5nmile
答案 D
解析 由题意知,在△ABC中AB=10,A=60°,B=75°,则C=180°-A-B=45°.
由正弦定理,得BC===5(nmile).
2.如图,一客轮以速率2v由A至B再到C匀速航行,一货船从AC的中点D出发,以速率v沿直线匀速航行,将货物送达客轮,已知AB⊥BC,AB=BC=50海里,若两船同时出发,则两船相遇之处M距C点的距离为( )
A.海里 B.海里
C.25海里 D.10海里
答案 A
解析 由题意知,M在BC上,设DM=x,则CM=100-2x,
在△CDM中,由余弦定理得:
x2=(25)2+(100-2x)2-2×25(100-2x)·cos45°,
解得x=50-,∴CM=.
3.从高出海平面h米的小岛看正东方向有一只船俯角为30°,看正南方向有一只船俯角为45°,则此时两船间的距离为( )
A.2h米B.h米C.h米D.2h米
答案 A
解析 如图所示,BC=h,AC=h,
∴AB==2h (米).
4.甲骑电动自行车以24km/h的速度沿着正北方向的公路行驶,在点A处望见电视塔S在电动车的北偏东30°方向上,15min后到点B处望见电视塔在电动车的北偏东75°方向上,则电动车在点B时与电视塔S的距离是( )
A.6kmB.3kmC.3kmD.3km
答案 C
解析 由题意知,AB=24×=6(km),∠BAS=30°,
∠ASB=75°-30°=45°.
由正弦定理,得
BS===3(km).
5.某货轮在A处看灯塔B在货轮北偏东75°,距离为12nmile;在A处看灯塔C在货轮的北偏西30°,距离为8nmile.货轮由A处向正北航行到D处时,再看灯塔B在南偏东60°,则A处与D处之间的距离为________nmile;灯塔C与D处之间的距离为________nmile.
答案 24 8
解析 (1)在△ABD中,由已知得∠ADB=60°,
∠B=45°;
由正弦定理得AD===24;
(2)在△ADC中,由余弦定理得CD2=AD2+AC2-2AD·ACcos30°,解得CD=8.
所以A处与D处之间的距离为24nmile,灯塔C与D处之间的距离为8nmile.
6.甲船在A处观察到乙船在它的北偏东60°方向的B处,两船相距anmile,乙船向正北方向行驶.若甲船的速度是乙船速度的倍,问甲船应沿什么方向前进才能最快追上乙船?相遇时乙船行驶多少nmile?
解 如图所示,设两船在C处相遇,并设∠CAB=θ,
乙船行驶距离BC为xnmile,
则AC=xnmile,
由正弦定理得sinθ==,而θ<60°,
∴θ=30°,即∠ACB=θ=30°,AB=BC=a,
从而BC==a (nmile).
答 甲船应沿北偏东30°方向前进才能最快追上乙船,两船相遇时乙船行驶了anmile.
7.某渔船在航行中不幸遇险,发出呼叫信号,我海军舰艇在A处获悉后,立即测出该渔船在方位角为45°,距离为10海里的C处,并测得渔船正沿方位角为105°的方向,以10海里/时的速度行驶,我海军舰艇立即以10海里/时的速度前去营救,求舰艇的航向和靠近渔船所需的时间.
解 如图所示,设舰艇与渔船在B处相遇时所用时间为t小时,
则AB=10t,CB=10t,
在△ABC中,根据余弦定理,则有
AB2=AC2+BC2-2AC·BCcos120°,
可得(10t)2=102+(10t)2-2×10×10tcos120°,
整理得2t2-t-1=0,解得t=1或t=-(舍去).
即舰艇需1小时靠近渔船,此时AB=10,BC=10,
在△ABC中,由正弦定理得=,
所以sin∠CAB===,
所以∠CAB=30°,所以舰艇航行的方位角为75°.
二、能力提升
8.台风中心从A地以20km/h的速度向东北方向移动,离台风中心30km内的地区为危险区,城市B在A的正东40km处,B城市处于危险区内的时间为( )
A.0.5hB.1hC.1.5hD.2h
答案 B
解析 设A地东北方向上点P到B的距离为30km,AP=x,在△ABP中,PB2=AP2+AB2-2AP·ABcosA,
即302=x2+402-2x·40cos45°,
化简得x2-40x+700=0.
设该方程的两根为x1,x2,
则|x1-x2|2=(x1+x2)2-4x1x2=400,
|x1-x2|=20,故t===1.故选B.
9.如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=________m.
答案 150
解析 根据图示,AC=100m.
在△MAC中,∠CMA=180°-75°-60°=45°.
由正弦定理得=?AM=100m.
在△AMN中,=sin60°,
∴MN=100×=150(m).
10.一船以每小时15km的速度向东航行,船在A处看到一个灯塔B在北偏东60°,行驶4h后,船到达C处,看到这个灯塔在北偏东15°,这时船与灯塔的距离为______km.
答案 30
解析 如图,由已知条件,
得AC=60km,∠BAC=30°,
∠ACB=105°,∠ABC=45°.
由正弦定理
BC=
=30(km).
11.某海上养殖基地A,接到气象部门预报,位于基地南偏东60°相距20(+1)海里的海面上有一台风中心,影响半径为20海里,正以每小时10海里的速度沿某一方向匀速直线前进,预计台风中心将从基地东北方向刮过且(+1)小时后开始影响基地持续2小时.求台风移动的方向.
解 如图所示,设预报时台风中心为B,开始影响基地时台风中心为C,基地刚好不受影响时台风中心为D,则B,C,D在一直线上,且AD=20,AC=20.
由题意AB=20(+1),DC=20,
BC=(+1)·10.
在△ADC中,∵DC2=AD2+AC2,
∴∠DAC=90°,∠ADC=45°.在△ABC中,
由余弦定理得cos∠BAC==.
∴∠BAC=30°,又∵B位于A南偏东60°,
60°+30°+90°=180°,∴D位于A的正北方向,
又∵∠ADC=45°,
∴台风移动的方向为向量的方向.即北偏西45°方向.
所以台风向北偏西45°方向移动.
12.如图,A,B是海面上位于东西方向相距5(+1)海里的两个观测点.现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20海里的C点的救援船立即前往营救,其航行速度为30海里/时,该救援船到达D点需要多长时间?
解 由题意知∠DBA=90°-60°=30°,∠DAB=90°-45°=45°,
∴∠ADB=180°-(45°+30°)=105°,
在△DAB中,由正弦定理得=,
∴DB===10(海里),
又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,BC=20(海里),
在△DBC中,由余弦定理得
CD2=BD2+BC2-2BD·BCcos∠DBC=300+1200-2×10×20×=900,
∴CD=30(海里),则需要的时间t==1(小时).
答 救援船到达D点需要1小时.
三、探究与创新
13.如图所示,A,B两个小岛相距21海里,B岛在A岛的正南方,现在甲船从A岛出发,以9海里的速度向B岛行驶,而乙船同时以6海里的速度离开B岛向南偏东60°方向行驶,问行驶多少时间后,两船相距最近,并求出两船的最近距离.
解 如图,行驶th后,甲船行驶了9t海里到达C处,乙船行驶了6t海里到达D处.
当9t<21,即t<时,C在线段AB上,此时BC=(21-9t)海里,
在△BCD中,BC=(21-9t)海里,BD=6t海里,
∠CBD=180°-60°=120°,
由余弦定理知CD2=BC2+BD2-2BC·BD·cos120°=(21-9t)2+(6t)2-2(21-9t)·6t·(-)
=63t2-252t+441=63(t-2)2+189.
当t=2时,CD取得最小值=3.
当t=时,C与B重合,
此时CD=6×=14(海里)>3(海里).
当t>时,BC=(9t-21)(海里),
则CD2=(9t-21)2+(6t)2-2×(9t-21)×6t·cos60°
=63t2-252t+441=63(t-2)2+189>189.
综上可知t=2时,CD取得最小值3.
答 行驶2h后,甲、乙两船相距最近为3海里.
