湘教版九年级数学上册第4章 锐角三角函数4.4 解直角三角形的应用教学课件(共28张)
文档属性
| 名称 | 湘教版九年级数学上册第4章 锐角三角函数4.4 解直角三角形的应用教学课件(共28张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-15 23:22:03 | ||
图片预览







文档简介
(共28张PPT)
解直角三角形的应用
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
某探险者某天到达如图所示的点A 处时,他准备估算出离他的目的地,海拔为3 500 m的山峰顶点B处的水平距离。同学们认为他能想出一个可行的办法吗?
为了帮助探险者解决这一问题,让我们开始今天的“解三角形”之旅吧。
.
A
B
.
02 新知探究
新知探究
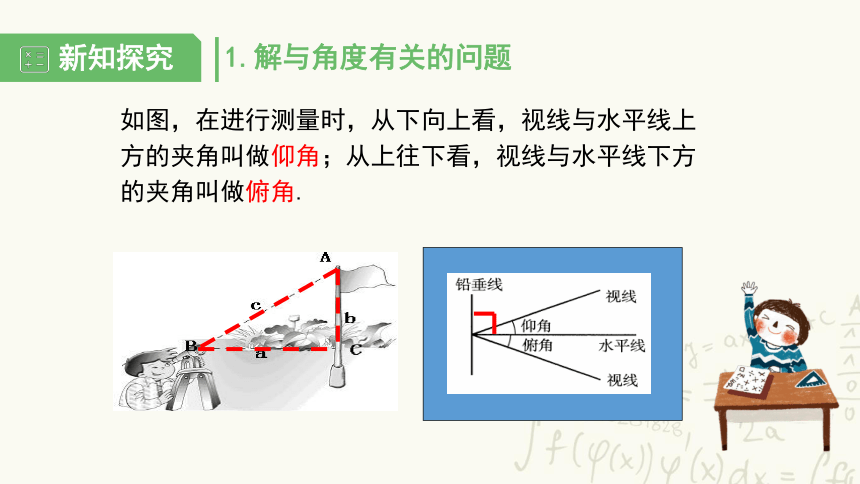
1.解与角度有关的问题
如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
新知探究
练一练
建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
解:在等腰Rt△BCD中,∠ACD=90°,BC=DC=40m.
在 Rt△ACD中 ,
∴AB=AC-BC=55.2-40=15.2 (m).
新知探究
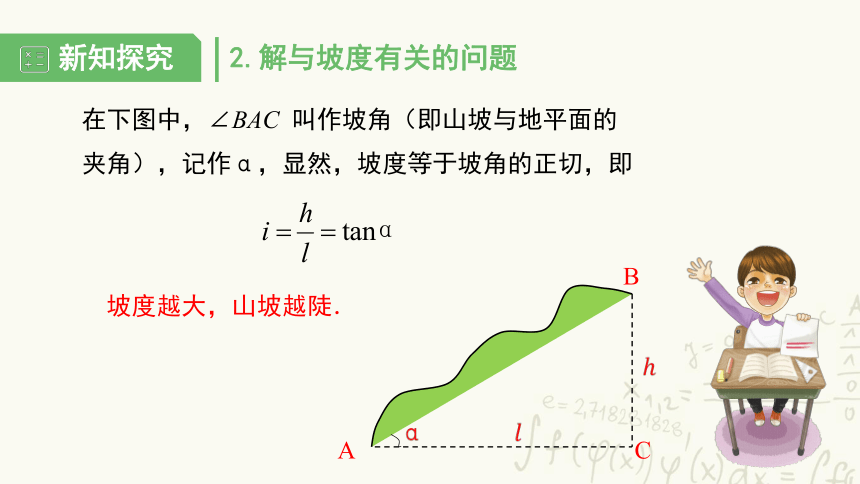
2.解与坡度有关的问题
如上图所示,从山坡脚下点 A 上坡走到点B时,升高的高度h(即线段BC的长度)与水平前进的距离l(即线段AC 的长度)的比叫作坡度,用字母i表示,即
(坡度通常写成1:m的形式).
A
B
C
新知探究
坡度越大,山坡越陡.
在下图中,∠BAC 叫作坡角(即山坡与地平面的
夹角),记作α,显然,坡度等于坡角的正切,即
2.解与坡度有关的问题
C
A
B
新知探究
练一练
1. 斜坡的坡度是 ,则坡角α =___度.
2. 斜坡的坡角是45° ,则坡比是 _____.
3. 斜坡长是12米,坡高6米,则坡比是_______.
30
1 : 1
新知探究
3.解与方位角有关的问题
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方位角. 如图所示:
30°
45°
B
O
A
东
西
北
南
45°
45°
西南
O
东北
东
西
北
南
西北
东南
北偏东30°
南偏西45°
新知探究
练一练
如图所示,A、B两城市相距200km.现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上.已知森林保护区的范围在以P点为圆心,100km为半径的圆形区域内,请问:计划修
筑的这条高速公路会
不会穿越保护区(参考
数据: ≈1.732,
≈1.414).
新知探究
练一练
200km
解:过点P作PC⊥AB,C是垂足.
则∠APC=30°,∠BPC=45°,
AC=PC·tan30°,BC=PC·tan45°.
∵AC+BC=AB,
∴PC · tan30°+PC · tan45°=200,
即 PC+PC=200,
解得 PC≈126.8km>100km.
答:计划修筑的这条高速公
路不会穿越保护区.
C
03 典型例题
1.要测量B点到河岸AD的距离,在A点测得∠BAD=30,在C点测得∠BCD=60,又测得AC=100米,测B点到河岸AD的距离为( )。
典型例题
A 100米
B 米
C 米
D 米
解析:过 B 作 BM⊥AD
∵∠BAD=30 ,∠BCD=60 ,
∴∠ABC=30 ∴AC-CB=100米,
∵ BM⊥AD,∴∠BMC=90 ,∴∠CBM=30
∴CM=CM=50米
M
B
典型例题
2.从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是 ( )
A.(6+6 )米 B. (6+3 )米
C. (6+2 )米 D. 12米
A
典型例题
3.如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 ( )
A.4km B.2 km
C.2 km D. ( +1)km
C
D
解析:作AD⊥OB,垂足为D,
很容易推断△BAD为等腰直角三角形,
AB == =2 km
4.一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度往前救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°=0.8,cos53°=0.6)
典型例题
C(游船)
A(港口)
B(海景船)
60°
37°
典型例题
解析:解直角三角形的应用-方向角问题
解:过C点作CD⊥AB交AB延长线于D.
在Rt△ACD中,∵∠ADC=90 ∠CAD=30,AC=80海里
∴CD=海里
在Rt△CBD中,∵∠CDB=90 ∠CBD=90-30,
∴BC=海里
∴海警船到大事故船C处所需的时间大约为
(小时)
C(游船)
A(港口)
B(海景船)
60°
37°
D
04 拓展提高
拓展提高
郴州北湖公园的小岛上有为了纪念唐代著名诗人韩愈而建的韩愈铜像,其底部为A,某人在岸边的B处测得A在B的北偏东60°的方向锁,然后沿岸边直行200米到达C处,再次测得A在C的北偏东30°的方向上(其中A,B,C在同一平面上).求这个铜像底部A到岸边BC的距离(结果精确到0.1米,参考数据)
解: 过A作AB⊥BC与D,则AD的长度就是A到岸边BC的距离
∵在岸边的B处测得A在B的北偏东60°的方向上
∴∠ABC=30°
D
拓展提高
∵A在C的北偏东30°的方向上
∴∠ACD=60°
∴BAC=30°
∴∠ABC=∠BAC
∴AC=BC=200
∵在Rt△ACD中,sin∠ACD=
∴sin60°=
∴AD=200sin60°=100≈173.2(米)
答:这个铜像底部A到岸边BC的距离是173.2米
D
05 课堂小结
课堂小结
模型一
模型二
模型三
模型四
仰角、俯角问题的常见基本模型:
A
D
B
E
C
课堂小结
解直角三角形的应用
坡度问题
方位角问题
坡角
坡度(或坡比)
角度问题
仰角
俯角
06 作业布置
1、巩固本章所学,熟练掌握锐角三角形求解
2、完成课本习题4.4 A、B组,并完成复习题4
作业布置
谢 谢 观 看
解直角三角形的应用
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
某探险者某天到达如图所示的点A 处时,他准备估算出离他的目的地,海拔为3 500 m的山峰顶点B处的水平距离。同学们认为他能想出一个可行的办法吗?
为了帮助探险者解决这一问题,让我们开始今天的“解三角形”之旅吧。
.
A
B
.
02 新知探究
新知探究
1.解与角度有关的问题
如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
新知探究
练一练
建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
解:在等腰Rt△BCD中,∠ACD=90°,BC=DC=40m.
在 Rt△ACD中 ,
∴AB=AC-BC=55.2-40=15.2 (m).
新知探究
2.解与坡度有关的问题
如上图所示,从山坡脚下点 A 上坡走到点B时,升高的高度h(即线段BC的长度)与水平前进的距离l(即线段AC 的长度)的比叫作坡度,用字母i表示,即
(坡度通常写成1:m的形式).
A
B
C
新知探究
坡度越大,山坡越陡.
在下图中,∠BAC 叫作坡角(即山坡与地平面的
夹角),记作α,显然,坡度等于坡角的正切,即
2.解与坡度有关的问题
C
A
B
新知探究
练一练
1. 斜坡的坡度是 ,则坡角α =___度.
2. 斜坡的坡角是45° ,则坡比是 _____.
3. 斜坡长是12米,坡高6米,则坡比是_______.
30
1 : 1
新知探究
3.解与方位角有关的问题
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方位角. 如图所示:
30°
45°
B
O
A
东
西
北
南
45°
45°
西南
O
东北
东
西
北
南
西北
东南
北偏东30°
南偏西45°
新知探究
练一练
如图所示,A、B两城市相距200km.现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上.已知森林保护区的范围在以P点为圆心,100km为半径的圆形区域内,请问:计划修
筑的这条高速公路会
不会穿越保护区(参考
数据: ≈1.732,
≈1.414).
新知探究
练一练
200km
解:过点P作PC⊥AB,C是垂足.
则∠APC=30°,∠BPC=45°,
AC=PC·tan30°,BC=PC·tan45°.
∵AC+BC=AB,
∴PC · tan30°+PC · tan45°=200,
即 PC+PC=200,
解得 PC≈126.8km>100km.
答:计划修筑的这条高速公
路不会穿越保护区.
C
03 典型例题
1.要测量B点到河岸AD的距离,在A点测得∠BAD=30,在C点测得∠BCD=60,又测得AC=100米,测B点到河岸AD的距离为( )。
典型例题
A 100米
B 米
C 米
D 米
解析:过 B 作 BM⊥AD
∵∠BAD=30 ,∠BCD=60 ,
∴∠ABC=30 ∴AC-CB=100米,
∵ BM⊥AD,∴∠BMC=90 ,∴∠CBM=30
∴CM=CM=50米
M
B
典型例题
2.从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是 ( )
A.(6+6 )米 B. (6+3 )米
C. (6+2 )米 D. 12米
A
典型例题
3.如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 ( )
A.4km B.2 km
C.2 km D. ( +1)km
C
D
解析:作AD⊥OB,垂足为D,
很容易推断△BAD为等腰直角三角形,
AB == =2 km
4.一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度往前救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°=0.8,cos53°=0.6)
典型例题
C(游船)
A(港口)
B(海景船)
60°
37°
典型例题
解析:解直角三角形的应用-方向角问题
解:过C点作CD⊥AB交AB延长线于D.
在Rt△ACD中,∵∠ADC=90 ∠CAD=30,AC=80海里
∴CD=海里
在Rt△CBD中,∵∠CDB=90 ∠CBD=90-30,
∴BC=海里
∴海警船到大事故船C处所需的时间大约为
(小时)
C(游船)
A(港口)
B(海景船)
60°
37°
D
04 拓展提高
拓展提高
郴州北湖公园的小岛上有为了纪念唐代著名诗人韩愈而建的韩愈铜像,其底部为A,某人在岸边的B处测得A在B的北偏东60°的方向锁,然后沿岸边直行200米到达C处,再次测得A在C的北偏东30°的方向上(其中A,B,C在同一平面上).求这个铜像底部A到岸边BC的距离(结果精确到0.1米,参考数据)
解: 过A作AB⊥BC与D,则AD的长度就是A到岸边BC的距离
∵在岸边的B处测得A在B的北偏东60°的方向上
∴∠ABC=30°
D
拓展提高
∵A在C的北偏东30°的方向上
∴∠ACD=60°
∴BAC=30°
∴∠ABC=∠BAC
∴AC=BC=200
∵在Rt△ACD中,sin∠ACD=
∴sin60°=
∴AD=200sin60°=100≈173.2(米)
答:这个铜像底部A到岸边BC的距离是173.2米
D
05 课堂小结
课堂小结
模型一
模型二
模型三
模型四
仰角、俯角问题的常见基本模型:
A
D
B
E
C
课堂小结
解直角三角形的应用
坡度问题
方位角问题
坡角
坡度(或坡比)
角度问题
仰角
俯角
06 作业布置
1、巩固本章所学,熟练掌握锐角三角形求解
2、完成课本习题4.4 A、B组,并完成复习题4
作业布置
谢 谢 观 看
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
