湘教版九年级数学上册第4章 锐角三角函数4.1 正弦和余弦教学课件(共41张)
文档属性
| 名称 | 湘教版九年级数学上册第4章 锐角三角函数4.1 正弦和余弦教学课件(共41张) |  | |
| 格式 | zip | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-15 23:25:54 | ||
图片预览










文档简介
(共41张PPT)
正弦和余弦
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
如图,是上海东方明珠电视塔的远景图,同学们能测量出它的高度吗?
小明不会计算呀。
在测量高度或者距离的问题的时候,我们一般可以利用锐角三角函数的相关知识来解决。通过这节课的学习我们就可以解决小明同学的问题了。
02 新知探究
新知探究
1.正弦的概念
为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上建一座扬水站,对坡面绿地进行喷灌. 先测得斜坡的坡脚 (∠A )为 30°,为使出水口的高度为 35 m,需要准备多长的水管?
30°
新知探究
1.正弦的概念
A
B
C
30°
35m
解:如图在 Rt△ABC 中,∠C=90°,∠A=30°, BC = 35 m,求AB.
根据“在直角三角形中,30°角所对的
边等于斜边的一半”. 即
可得 AB = 2BC =70 (m). 即需要准备 70 m 长的水管.
在直角三角形中,如果一个锐角等于30°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于 .
新知探究
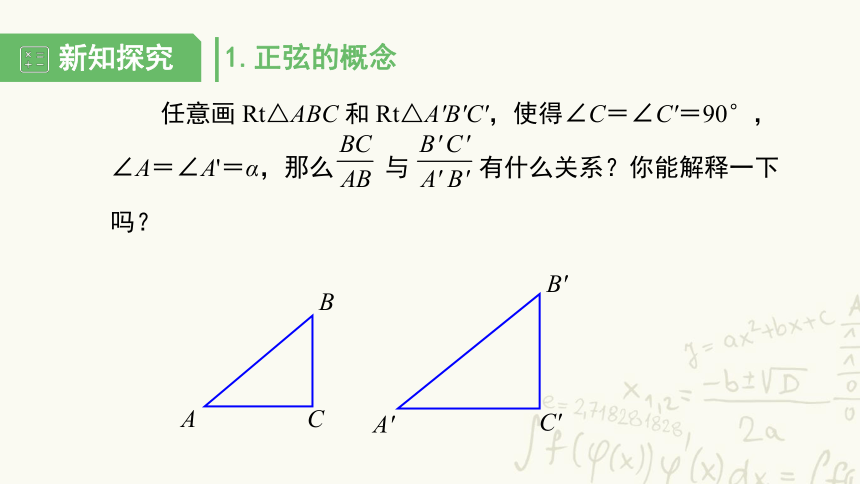
任意画 Rt△ABC 和 Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系?你能解释一下吗?
A
B
C
A'
B'
C'
1.正弦的概念
新知探究
因为∠C=∠C'=90°,∠A=∠A'=α,所以Rt△ABC ∽Rt△A'B'C'. 所以
这就是说,在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A 的对边与斜边的比也是一个固定值.
1.正弦的概念
新知探究
如图,在 Rt△ABC 中,∠C=90°,我们把锐角 A 的对边与斜边的比叫做∠A的正弦,记作 sin A 即
例如,当∠A=30°时,我们有
A
B
C
c
a
b
对边
斜边
∠A的对边
斜边
sin A =
1.正弦的概念
新知探究
练一练
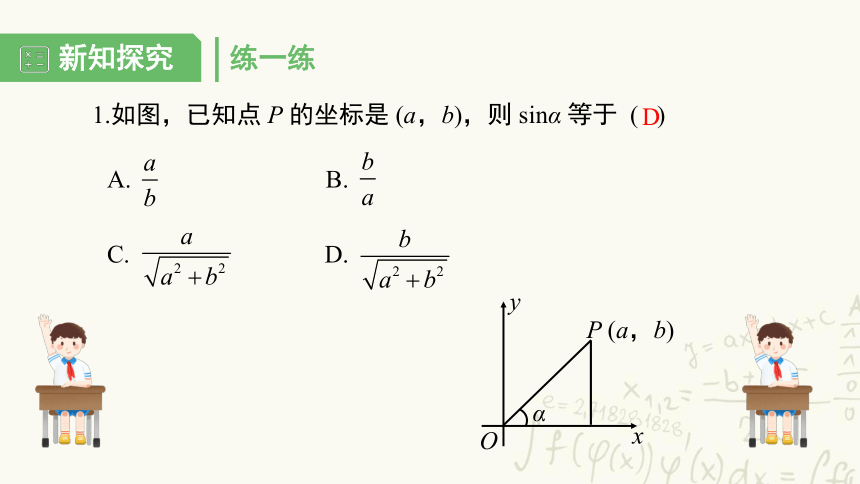
1.如图,已知点 P 的坐标是 (a,b),则 sinα 等于 ( )
O
x
y
P (a,b)
α
A. B.
C. D.
D
新知探究
正弦的简单应用
如图,在 Rt△ABC 中,∠C=90°, ,BC = 3,求 sinB 及 Rt△ABC 的面积.
A
B
C
提示:已知 sinA 及∠A的对边 BC 的长度,可以求出斜边 AB 的长. 然后再利用勾股定理,求出 BC 的长度,进而求出 sinB 及 Rt△ABC 的面积.
新知探究
2.正弦的简单应用
解:∵ ∴
∴ AB = 3BC =3×3=9.
∴
∴
∴
新知探究
小归纳
在 Rt△ABC 中,∠C = 90°,sinA = k,sinB = h,AB = c,则
BC = ck,
AC = ch.
在 Rt△ABC 中,∠C = 90°,sinA = k,sinB = h,BC=a,则
AB =
AC =
新知探究
练一练
2. 在Rt△ABC中,∠C=90°,sinA= ,BC=6,则
AB 的长为 ( )
D
A. 4 B. 6 C. 8 D. 10
3. 在△ABC中,∠C=90°,如果 sinA = ,AB=6,
那么BC=___.
2
新知探究
特殊角的正弦值
如何求sin 45°的值?
如图所示,构造一个Rt△ABC,使∠C=90°,∠A=45°.
于是∠B=45°.
从而AC=BC.
根据勾股定理,得
AB2=AC2+BC2=BC2+BC2=2BC2.
于是AB= BC.
因此sin45°=
新知探究
小归纳
30°、45°、60°角的正弦值如下表:
锐角a
三角
函数 30° 45° 60°
sin a
新知探究
利用计算器求正弦值
例如:求50°角的正弦值,可以在计算器上依次按键
,显示结果为0.7660…
至此,我们已经知道了三个特殊角(30°,45°,60°)的正弦值,而对于一般锐角α的正弦值,我们可以利用计算器来求.
新知探究
做一做
已知sinA=0.501 8,用计算器求锐角A可以按照下面方法操作:
第一步:按计算器 键,
第二步:然后输入函数值0. 501 8
屏幕显示答案: 30.119 158 67°
2nd F
sin
新知探究
2.余弦
在有一个锐角相等的所有直角三角形中,这个锐角的邻边与斜边的比值是一个常数,与直角三角形的大小无关.
如下图所示,在直角三角形中,我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即
A
B
C
斜边
邻边
∠A的邻边
斜边
cos A =
新知探究
小归纳
1.sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sinA、 cosA是一个比值(数值).
3.sinA、 cosA的大小只与∠A的大小有关,而与直角三角形的边长无关.
新知探究
练一练
4. 求 cos30°,cos60°,cos45°的值.
解:cos30°= sin (90°-30°) = sin60° = ;
cos60°= sin (90°-60°) = sin30°=
cos45°= sin (90°-45°) = sin45°=
新知探究
练一练
5.在Rt△ABC中,∠C=90°,如图,已知AC=3,AB=6,
求sinA和cosB.
┌
B
C
A
3
6
想一想:我们发现sinA=cosB,其中有没有什么内在的关系?
解:在Rt△ABC中,∵AB=6,AC=3
∴
∴
新知探究
小归纳
从上述探究和证明过程看出,对于任意锐角α,有
cos α = sin (90°-α)
从而有
sin α = cos (90°-α)
新知探究
小归纳
如图:在Rt △ABC中,∠C=90°,
sinA=cosB
A
B
C
∠A 的对边a
∠A 的邻边b
c
新知探究
如图:在Rt △ABC中,∠C=90°,
B
A
C
∠A 的对边a
∠A 的邻边b
小归纳
03 典型例题
典型例题
1.在Rt△ABC 中,∠C=90°,∠A=30°,则 的值是 ( )
A
2.如图,在Rt△ABC 中,∠C=90°,AB=5,BC=4,则sinB的值是 ( )
D
典型例题
3.如果△ABC中,sinA=cosB= ,则下列最准确的结论是( )
C
A △ABC是直角三角形
B △ABC是等腰三角形
C △ABC是等腰直角三角形
D △ABC是锐角三角形
4.如图,在平面直角坐标系内有一点 P (3,4),连接 OP,求 OP 与 x 轴正方向所夹锐角 α 的正弦值.
解:如图,设点 A (3,0),连接 PA .
A (0,3)
在△APO中,由勾股定理得
=5
因此
α
方法总结:结合平面直角坐标系求某角的正弦函数值,一般过已知点向x轴或y轴作垂线,构造直角三角形,再结合勾股定理求解.
典型例题
5.在△ABC中,∠C=90°,BC=24cm,cosA= ,求这个三角形的周长.
典型例题
解:cosA=,BC=24
∴
∴ =2
∴
∴ △ABC60cm
04 拓展提高
拓展提高
如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一动点(不与点A,B重合),DP交AC与点Q.
(1)求证:△APQ∽△CDQ
(2)当PD⊥AC时,求线段PA的长度
(3)当点P在线段AC的垂直平分线上时,求sin∠CPB的值
解:(1)∵四边形ABCD是矩形,∴DC∥AB
∴∠QAP=∠QCD,∠QPA=∠QDC,
∴△APQ∽△CDQ
拓展提高
解:(2)∵PD⊥AC,∴∠QDC+∠QCD=90°又∠QDC+∠QDA=90°
(2)当PD⊥AC时,求线段PA的长度
∴∠QCD=∠QDA,又∠DAP=∠CDA=90°,
∴△DAP∽△CDA
∴ ,即
解得 AP=
拓展提高
解:(3)连接PC
(3)当点P在线段AC的垂直平分线上时,求sin∠CPB的值
∵点P在线段AC的垂直平分线上
∴PC=PA
设PA= ,则PC= ,PB=10-
由勾股定理得,PC2=PB2+BC2,即
解得=
∴PC=PA=
∴sin∠CPB=
05 课堂小结
课堂小结
正弦函数
正弦函数的概念
正弦函数的应用
已知边长求正弦值
已知正弦值求边长
∠A的对边
斜边
sin A =
课堂小结
余弦
余弦的概念:在直角三角形中,锐角α的邻边与斜边的比叫做角α的余弦
余弦的性质:α确定的情况下,cosα为定值,与三角形的大小无关
用计算器解决余弦问题
06 作业布置
1、巩固本节所学
2、完成课本习题 4.1 A、B组
作业布置
谢 谢 观 看
正弦和余弦
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
如图,是上海东方明珠电视塔的远景图,同学们能测量出它的高度吗?
小明不会计算呀。
在测量高度或者距离的问题的时候,我们一般可以利用锐角三角函数的相关知识来解决。通过这节课的学习我们就可以解决小明同学的问题了。
02 新知探究
新知探究
1.正弦的概念
为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上建一座扬水站,对坡面绿地进行喷灌. 先测得斜坡的坡脚 (∠A )为 30°,为使出水口的高度为 35 m,需要准备多长的水管?
30°
新知探究
1.正弦的概念
A
B
C
30°
35m
解:如图在 Rt△ABC 中,∠C=90°,∠A=30°, BC = 35 m,求AB.
根据“在直角三角形中,30°角所对的
边等于斜边的一半”. 即
可得 AB = 2BC =70 (m). 即需要准备 70 m 长的水管.
在直角三角形中,如果一个锐角等于30°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于 .
新知探究
任意画 Rt△ABC 和 Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系?你能解释一下吗?
A
B
C
A'
B'
C'
1.正弦的概念
新知探究
因为∠C=∠C'=90°,∠A=∠A'=α,所以Rt△ABC ∽Rt△A'B'C'. 所以
这就是说,在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A 的对边与斜边的比也是一个固定值.
1.正弦的概念
新知探究
如图,在 Rt△ABC 中,∠C=90°,我们把锐角 A 的对边与斜边的比叫做∠A的正弦,记作 sin A 即
例如,当∠A=30°时,我们有
A
B
C
c
a
b
对边
斜边
∠A的对边
斜边
sin A =
1.正弦的概念
新知探究
练一练
1.如图,已知点 P 的坐标是 (a,b),则 sinα 等于 ( )
O
x
y
P (a,b)
α
A. B.
C. D.
D
新知探究
正弦的简单应用
如图,在 Rt△ABC 中,∠C=90°, ,BC = 3,求 sinB 及 Rt△ABC 的面积.
A
B
C
提示:已知 sinA 及∠A的对边 BC 的长度,可以求出斜边 AB 的长. 然后再利用勾股定理,求出 BC 的长度,进而求出 sinB 及 Rt△ABC 的面积.
新知探究
2.正弦的简单应用
解:∵ ∴
∴ AB = 3BC =3×3=9.
∴
∴
∴
新知探究
小归纳
在 Rt△ABC 中,∠C = 90°,sinA = k,sinB = h,AB = c,则
BC = ck,
AC = ch.
在 Rt△ABC 中,∠C = 90°,sinA = k,sinB = h,BC=a,则
AB =
AC =
新知探究
练一练
2. 在Rt△ABC中,∠C=90°,sinA= ,BC=6,则
AB 的长为 ( )
D
A. 4 B. 6 C. 8 D. 10
3. 在△ABC中,∠C=90°,如果 sinA = ,AB=6,
那么BC=___.
2
新知探究
特殊角的正弦值
如何求sin 45°的值?
如图所示,构造一个Rt△ABC,使∠C=90°,∠A=45°.
于是∠B=45°.
从而AC=BC.
根据勾股定理,得
AB2=AC2+BC2=BC2+BC2=2BC2.
于是AB= BC.
因此sin45°=
新知探究
小归纳
30°、45°、60°角的正弦值如下表:
锐角a
三角
函数 30° 45° 60°
sin a
新知探究
利用计算器求正弦值
例如:求50°角的正弦值,可以在计算器上依次按键
,显示结果为0.7660…
至此,我们已经知道了三个特殊角(30°,45°,60°)的正弦值,而对于一般锐角α的正弦值,我们可以利用计算器来求.
新知探究
做一做
已知sinA=0.501 8,用计算器求锐角A可以按照下面方法操作:
第一步:按计算器 键,
第二步:然后输入函数值0. 501 8
屏幕显示答案: 30.119 158 67°
2nd F
sin
新知探究
2.余弦
在有一个锐角相等的所有直角三角形中,这个锐角的邻边与斜边的比值是一个常数,与直角三角形的大小无关.
如下图所示,在直角三角形中,我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即
A
B
C
斜边
邻边
∠A的邻边
斜边
cos A =
新知探究
小归纳
1.sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sinA、 cosA是一个比值(数值).
3.sinA、 cosA的大小只与∠A的大小有关,而与直角三角形的边长无关.
新知探究
练一练
4. 求 cos30°,cos60°,cos45°的值.
解:cos30°= sin (90°-30°) = sin60° = ;
cos60°= sin (90°-60°) = sin30°=
cos45°= sin (90°-45°) = sin45°=
新知探究
练一练
5.在Rt△ABC中,∠C=90°,如图,已知AC=3,AB=6,
求sinA和cosB.
┌
B
C
A
3
6
想一想:我们发现sinA=cosB,其中有没有什么内在的关系?
解:在Rt△ABC中,∵AB=6,AC=3
∴
∴
新知探究
小归纳
从上述探究和证明过程看出,对于任意锐角α,有
cos α = sin (90°-α)
从而有
sin α = cos (90°-α)
新知探究
小归纳
如图:在Rt △ABC中,∠C=90°,
sinA=cosB
A
B
C
∠A 的对边a
∠A 的邻边b
c
新知探究
如图:在Rt △ABC中,∠C=90°,
B
A
C
∠A 的对边a
∠A 的邻边b
小归纳
03 典型例题
典型例题
1.在Rt△ABC 中,∠C=90°,∠A=30°,则 的值是 ( )
A
2.如图,在Rt△ABC 中,∠C=90°,AB=5,BC=4,则sinB的值是 ( )
D
典型例题
3.如果△ABC中,sinA=cosB= ,则下列最准确的结论是( )
C
A △ABC是直角三角形
B △ABC是等腰三角形
C △ABC是等腰直角三角形
D △ABC是锐角三角形
4.如图,在平面直角坐标系内有一点 P (3,4),连接 OP,求 OP 与 x 轴正方向所夹锐角 α 的正弦值.
解:如图,设点 A (3,0),连接 PA .
A (0,3)
在△APO中,由勾股定理得
=5
因此
α
方法总结:结合平面直角坐标系求某角的正弦函数值,一般过已知点向x轴或y轴作垂线,构造直角三角形,再结合勾股定理求解.
典型例题
5.在△ABC中,∠C=90°,BC=24cm,cosA= ,求这个三角形的周长.
典型例题
解:cosA=,BC=24
∴
∴ =2
∴
∴ △ABC60cm
04 拓展提高
拓展提高
如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一动点(不与点A,B重合),DP交AC与点Q.
(1)求证:△APQ∽△CDQ
(2)当PD⊥AC时,求线段PA的长度
(3)当点P在线段AC的垂直平分线上时,求sin∠CPB的值
解:(1)∵四边形ABCD是矩形,∴DC∥AB
∴∠QAP=∠QCD,∠QPA=∠QDC,
∴△APQ∽△CDQ
拓展提高
解:(2)∵PD⊥AC,∴∠QDC+∠QCD=90°又∠QDC+∠QDA=90°
(2)当PD⊥AC时,求线段PA的长度
∴∠QCD=∠QDA,又∠DAP=∠CDA=90°,
∴△DAP∽△CDA
∴ ,即
解得 AP=
拓展提高
解:(3)连接PC
(3)当点P在线段AC的垂直平分线上时,求sin∠CPB的值
∵点P在线段AC的垂直平分线上
∴PC=PA
设PA= ,则PC= ,PB=10-
由勾股定理得,PC2=PB2+BC2,即
解得=
∴PC=PA=
∴sin∠CPB=
05 课堂小结
课堂小结
正弦函数
正弦函数的概念
正弦函数的应用
已知边长求正弦值
已知正弦值求边长
∠A的对边
斜边
sin A =
课堂小结
余弦
余弦的概念:在直角三角形中,锐角α的邻边与斜边的比叫做角α的余弦
余弦的性质:α确定的情况下,cosα为定值,与三角形的大小无关
用计算器解决余弦问题
06 作业布置
1、巩固本节所学
2、完成课本习题 4.1 A、B组
作业布置
谢 谢 观 看
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
