湘教版九年级数学上册第4章 锐角三角函数4.3 解直角三角形教学课件(共24张)
文档属性
| 名称 | 湘教版九年级数学上册第4章 锐角三角函数4.3 解直角三角形教学课件(共24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-16 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
解直角三角形
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
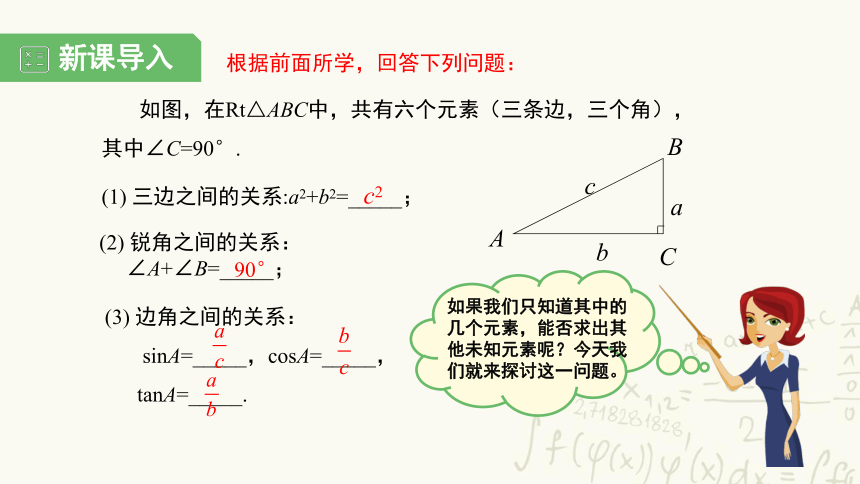
新课导入
根据前面所学,回答下列问题:
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2=_____;
(2) 锐角之间的关系:
∠A+∠B=_____;
(3) 边角之间的关系:
sinA=_____,cosA=_____,
tanA=_____.
如图,在Rt△ABC中,共有六个元素(三条边,三个角), 其中∠C=90°.
c2
90°
如果我们只知道其中的几个元素,能否求出其他未知元素呢?今天我们就来探讨这一问题。
02 新知探究
新知探究
1.在图中的Rt△ABC中,
(1) 根据∠A=75°,斜边AB=6,你能求出这个直角三角形的其他元素吗?
A
B
C
6
75°
1.已知一锐角和一边求其他元素
新知探究
2. 根据AC=2.4,斜边AB=6,你能求出这个直角三角形的其他元素吗?
A
B
C
6
2.4
2.已知两边求其他元素
根据∠A+∠B=90°,
∴∠B=90°-66°=24°
新知探究
解直角三角形的概念
在直角三角形中,除直角外有5个元素(即3条边、2个锐角),只要知道其中的2个元素(至少有1个是边),就可以求出其余的3个未知元素.
由直角三角形中的已知元素,求出其余未知元素的过程,叫作解直角三角形.
新知探究
解直角三角形的概念
想一想:如果只知道直角三角形的两个角,可以求出其余未知元素吗?
答:已知两个角不行,
相似直角三角形的角都相等,但是边的大小却不同。
不能求出其余的元素。
新知探究
练一练
1.如图,已知 AC = 4,求 AB 和 BC 的长.
提示:作CD⊥AB于点D,根据三角函数的定义,在Rt△ACD,Rt△CDB中,即可求出 CD,AD,BD 的长,从而求解.
新知探究
练一练
在Rt△CDB中,∵∠DCB=∠ACB-∠ACD=45°,
D
解:如图,作CD⊥AB于点D,
在Rt△ACD中,∵∠A=30°,∴∠ACD=90°-∠A=60°,
∴BD=CD=2.
新知探究
2.如图,在Rt△ABC 中,∠C=90°,cosA = ,BC = 5, 试求AB的长.
A
C
B
解:
设
练一练
∴ AB的长为
∵,
∴,
∴, (舍去)
03 典型例题
典型例题
1.如图,Rt△ABC中,∠C=90°,BC=15,tanA=。则
AB=______.
C
A
B
17
解析:因为BC=15,tanA=,
所以,AC=8,有勾股定理得 AB=17
2.如图,在平面直角坐标系中,点A的坐标为(3,4),那么的值是( )。
典型例题
【考点】解直角三角形,坐标与图形性质
B.
C.
D.
A.
解:作AB⊥x轴于B,如图,
∵点A的坐标为(3,4),
∴OB=3,AB=4
∴OA==
C
3.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了______米。(参考数据sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
典型例题
解:在Rt△ABC中,sin34°=
∴AC=AB
280
04 拓展提高
拓展提高
一艘轮船位于灯塔P南偏西60°方向的A出,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)
【考点】解直角三角形的应用-方向角问题
勾股定理的应用
拓展提高
解:如图,作AC⊥PC,∠APC=60°,∠BPC=45°,AP=200
在Rt△APC中,∵cos∠APC=
∴PC=20cos
∴AC=
在△PBC中,∵∠BPC=45°
∴△BPC为等腰直角三角形,∴BC=PC=10
∴AB=AC-BC=
答:轮船航行途中与灯塔P的最短距离是( )海里
C
05 课堂小结
课堂小结
解直角三角形
依据
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素
勾股定理
两锐角互余
锐角的三角函数
06 作业布置
完成课本习题 4.3 A、B组
作业布置
谢 谢 观 看
解直角三角形
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
根据前面所学,回答下列问题:
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2=_____;
(2) 锐角之间的关系:
∠A+∠B=_____;
(3) 边角之间的关系:
sinA=_____,cosA=_____,
tanA=_____.
如图,在Rt△ABC中,共有六个元素(三条边,三个角), 其中∠C=90°.
c2
90°
如果我们只知道其中的几个元素,能否求出其他未知元素呢?今天我们就来探讨这一问题。
02 新知探究
新知探究
1.在图中的Rt△ABC中,
(1) 根据∠A=75°,斜边AB=6,你能求出这个直角三角形的其他元素吗?
A
B
C
6
75°
1.已知一锐角和一边求其他元素
新知探究
2. 根据AC=2.4,斜边AB=6,你能求出这个直角三角形的其他元素吗?
A
B
C
6
2.4
2.已知两边求其他元素
根据∠A+∠B=90°,
∴∠B=90°-66°=24°
新知探究
解直角三角形的概念
在直角三角形中,除直角外有5个元素(即3条边、2个锐角),只要知道其中的2个元素(至少有1个是边),就可以求出其余的3个未知元素.
由直角三角形中的已知元素,求出其余未知元素的过程,叫作解直角三角形.
新知探究
解直角三角形的概念
想一想:如果只知道直角三角形的两个角,可以求出其余未知元素吗?
答:已知两个角不行,
相似直角三角形的角都相等,但是边的大小却不同。
不能求出其余的元素。
新知探究
练一练
1.如图,已知 AC = 4,求 AB 和 BC 的长.
提示:作CD⊥AB于点D,根据三角函数的定义,在Rt△ACD,Rt△CDB中,即可求出 CD,AD,BD 的长,从而求解.
新知探究
练一练
在Rt△CDB中,∵∠DCB=∠ACB-∠ACD=45°,
D
解:如图,作CD⊥AB于点D,
在Rt△ACD中,∵∠A=30°,∴∠ACD=90°-∠A=60°,
∴BD=CD=2.
新知探究
2.如图,在Rt△ABC 中,∠C=90°,cosA = ,BC = 5, 试求AB的长.
A
C
B
解:
设
练一练
∴ AB的长为
∵,
∴,
∴, (舍去)
03 典型例题
典型例题
1.如图,Rt△ABC中,∠C=90°,BC=15,tanA=。则
AB=______.
C
A
B
17
解析:因为BC=15,tanA=,
所以,AC=8,有勾股定理得 AB=17
2.如图,在平面直角坐标系中,点A的坐标为(3,4),那么的值是( )。
典型例题
【考点】解直角三角形,坐标与图形性质
B.
C.
D.
A.
解:作AB⊥x轴于B,如图,
∵点A的坐标为(3,4),
∴OB=3,AB=4
∴OA==
C
3.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了______米。(参考数据sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
典型例题
解:在Rt△ABC中,sin34°=
∴AC=AB
280
04 拓展提高
拓展提高
一艘轮船位于灯塔P南偏西60°方向的A出,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)
【考点】解直角三角形的应用-方向角问题
勾股定理的应用
拓展提高
解:如图,作AC⊥PC,∠APC=60°,∠BPC=45°,AP=200
在Rt△APC中,∵cos∠APC=
∴PC=20cos
∴AC=
在△PBC中,∵∠BPC=45°
∴△BPC为等腰直角三角形,∴BC=PC=10
∴AB=AC-BC=
答:轮船航行途中与灯塔P的最短距离是( )海里
C
05 课堂小结
课堂小结
解直角三角形
依据
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素
勾股定理
两锐角互余
锐角的三角函数
06 作业布置
完成课本习题 4.3 A、B组
作业布置
谢 谢 观 看
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
