湘教版九年级数学上册第3章 图形的相似3.4.2 相似三角形的性质教学课件(共34张)
文档属性
| 名称 | 湘教版九年级数学上册第3章 图形的相似3.4.2 相似三角形的性质教学课件(共34张) |  | |
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-16 12:34:53 | ||
图片预览








文档简介
(共34张PPT)
相似三角形的性质
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
通过前面的学习,我们已经知道,相似三角形的对应角相等、对应边成比例,但是对于三角形而言,还具有哪些特殊的几何度量呢?
新课导入
还有三角形的高、角平分线、中线和面积
今天,我们就来探究一下如果两个三角形相似,它们的几何度量是符合怎样的关系的。
02 新知探究
新知探究
1.相似三角形对应高的比等于相似比
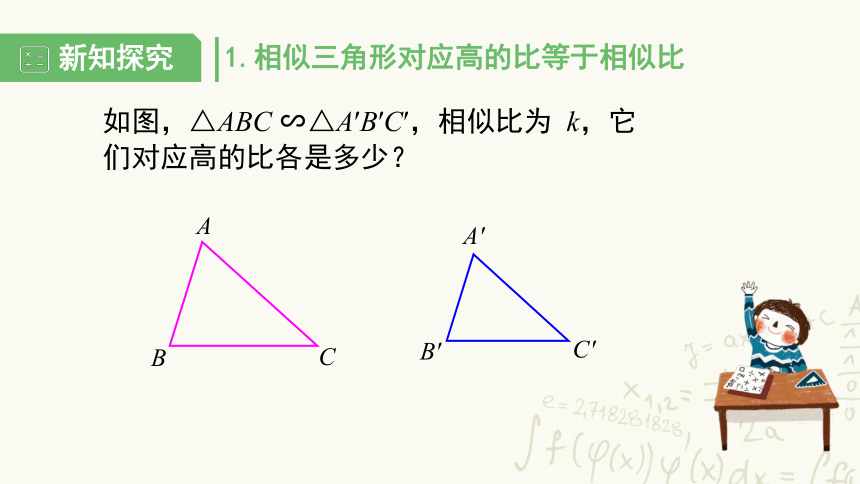
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高的比各是多少?
A
B
C
A'
B'
C'
新知探究
1.相似三角形对应高的比等于相似比
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
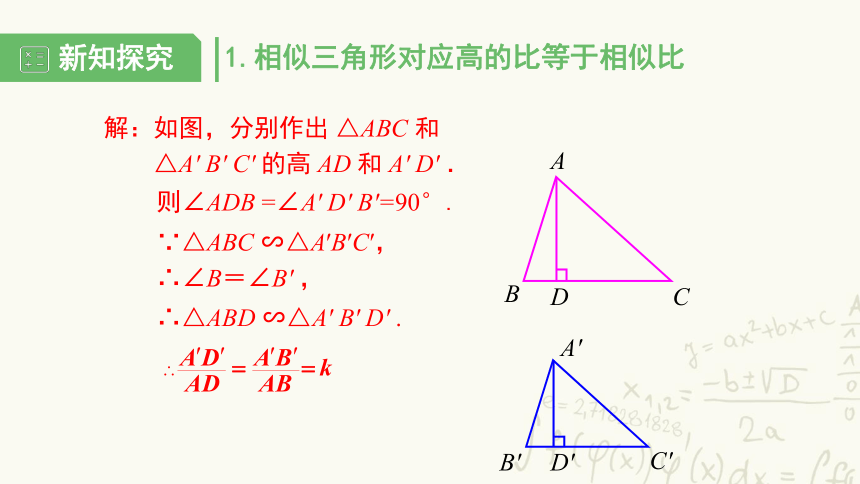
解:如图,分别作出 △ABC 和
△A' B' C' 的高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
新知探究
小归纳
由此得到:
相似三角形对应高的比等于相似比.
类似的,我们可以得到其余两组对应边上的高的比也等于相似比.
新知探究
练一练
ΔABC∽ ΔA1B1C1 ,BD和B1D1是它们的中线,
已知 ,B1D1 =4cm,则BD= cm.
6
2.ΔABC∽ ΔA1B1C1, AD和A1D1是对应角平分
线,已知AD=8cm, A1D1=3cm ,则 ΔABC与
ΔA1B1C1的对应高之比为 .
8:3
新知探究
2.相似三角形对应角平分线的比、
对应中线的比都等于相似比
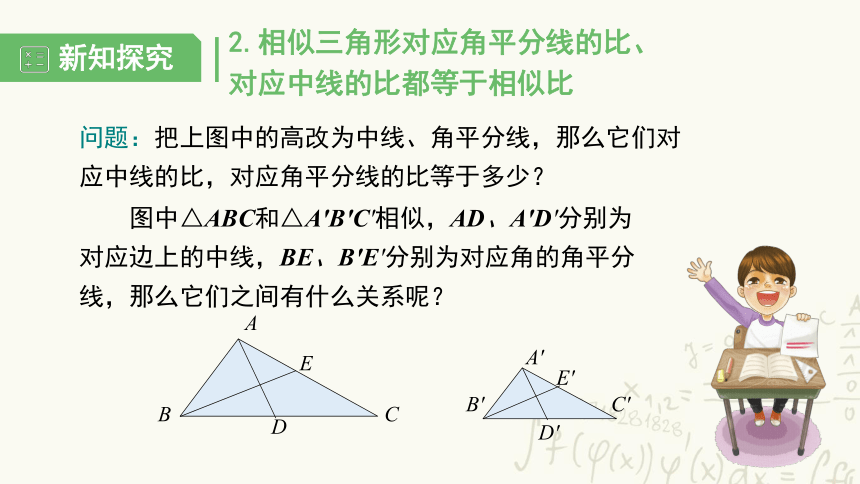
问题:把上图中的高改为中线、角平分线,那么它们对应中线的比,对应角平分线的比等于多少?
图中△ABC和△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的角平分线,那么它们之间有什么关系呢?
A
B
C
D
E
A'
B'
D'
C'
E'
新知探究
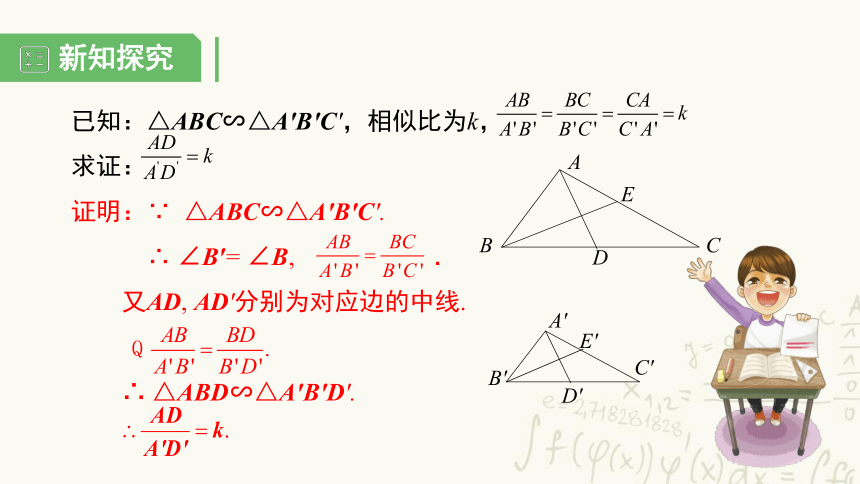
已知:△ABC∽△A′B′C′,相似比为k,
求证:
证明:∵ △ABC∽△A′B′C′.
∴ ∠B′= ∠B, .
又AD, AD′分别为对应边的中线.
∴ △ABD∽△A′B′D′.
A'
B'
D'
C'
E'
A
B
C
D
E
新知探究
小归纳
由此得到:
相似三角形对应角平分线的比和对应的中线的比也等于相似比.
类似地,可以得到另外两组对应角平分线和对应中线的比也等于相似比.
新知探究
练一练
3.两个相似三角形的两条对应边的长分别是6cm和8cm,如果它们对应的两条角平分线的和为42cm,那么这两条角平分线的长分别是多少?
解:设较短的角平分线长为xcm,
则由相似性质有 .
解得x=18.
较长的角平分线长为24cm.
故这两条角平分线的长分别为18cm,24cm.
新知探究
思考:通过前面的学习我们知道,如果两个三角形相似,它们对应高的比、对应中线的比和对应角平分线的比都等于相似比.那么它们周长的比之间有什么关系?也等于相似比吗?面积之比呢?
A
B
C
A1
B1
C1
3.相似三角形的周长比等于相似比
新知探究
3.相似三角形的周长比等于相似比
思考:图中(1)(2)(3)分别是边长为1,2,3的等边三角形,它们都相似吗?
(1)
(2)
(3)
1
2
3
(1)与(2)的相似比=______,
(1)与(2)的周长比=______,
(1)与(3)的相似比=______,
(1)与(3)的周长比=______.
1∶ 2
结论: 相似三角形的周长比等于相似比。
(都相似)
1∶ 3
1∶ 2
1∶ 3
新知探究
想一想
证明:设△ABC∽△A1B1C1,相似比为k
求证:相似三角形的周长比等于相似比.
A
B
C
A1
B1
C1
思考:怎么证明这一结论呢?
有
相似三角形周长的比等于相似比.
新知探究
解:设△ABC∽△A′B′C′,相似比为k,
分别作出△ABC和△A′B′C′的高AD和A′D′.
∵△ABC和△A′B′C′都是直角三角形,并且∠B=∠B′,
∴△ABD∽△A′B′D′.
A
B
C
A′
B′
C′
D
D′
思考:如果两个相似三角形的相似比为k ,
那么面积比是什么呢?
∵△ABC∽△A′B′C′.
4.相似三角形的面积比等于相似比的平方
∴
新知探究
小归纳
相似三角形的面积比等于相似比的平方.
新知探究
练一练
4.已知ΔABC与ΔA′B′C′的相似比为2:3,则对
应边上中线之比 ,面积之比为 .
4. 如果两个相似三角形的面积之比为1:9,
周长的比为______ .
1:3
2:3
4:9
03 典型例题
3.两个相似三角形对应中线的比为 ,
则对应高的比为______ .
2.相似三角形对应边的比为2∶3,那么对应角的角平分线的比为______.
2∶ 3
1.两个相似三角形的相似比为 , 则对应高的比为_________, 则对应中线的比为_________.
典型例题
解:∵ △ABC∽△DEF,
解得,EH=3.2(cm).
答:EH的长为3.2cm.
A
G
B
C
D
E
F
H
4.已知△ABC∽△DEF,BG、EH分△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
典型例题
5. 如图,是一个照相机成像的示意图.
(1)如果像高MN是35mm,焦距是50mm,拍摄的景物高度AB是4.9m,拍摄点离景物由多远?
解:(1)根据物体成像原理知:△LMN ∽△LBA,
∴ ,
∵ 像高MN为35mm,焦距是50mm,
拍摄的景物高度AB是4.9m,
∴ ,解得LD=7,∴拍摄点距景物7m
典型例题
(2)拍摄高度是2m的景物,拍摄点离景物有4m,像高不变
∴ ,解得LC=70
∴ 相机的焦距应调整为70mm
典型例题
(2)如果要完整的拍摄高度是2m的景物,拍摄点离景物有4m,像高不变,则相机的焦距应调整为多少毫米?
04 拓展提高
拓展提高
如图,△ABC 中,DE∥BC,DE 分别交 AB、AC 于
点 D、E,S△ADE=2 S△DCE,求 S△ADE ∶S△ABC.
解:过点 D 作 AC 的垂线,交点为 F,则
∴
又∵ DE∥BC,
∴ △ADE ∽△ABC.
A
B
C
D
E
F
拓展提高
∴
即 S△ADE : S△ABC =4 : 9.
05 课堂小结
课堂小结
相似三角形的性质1
相似三角形对应高的比等于相似比
相似三角形对应角平分线的比等于相似比
相似三角形对应中线的比等于相似比
课堂小结
相似三角形的性质2
相似三角形周长之比等于相似比
相似三角形面积之比等于相似比的平方
06 作业布置
1、完成课本习题 3.4 A、B组
2、熟记相似三角形的性质,熟练的掌握周长、面积与相似比之间的关系。
作业布置
谢 谢 观 看
相似三角形的性质
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
通过前面的学习,我们已经知道,相似三角形的对应角相等、对应边成比例,但是对于三角形而言,还具有哪些特殊的几何度量呢?
新课导入
还有三角形的高、角平分线、中线和面积
今天,我们就来探究一下如果两个三角形相似,它们的几何度量是符合怎样的关系的。
02 新知探究
新知探究
1.相似三角形对应高的比等于相似比
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高的比各是多少?
A
B
C
A'
B'
C'
新知探究
1.相似三角形对应高的比等于相似比
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
解:如图,分别作出 △ABC 和
△A' B' C' 的高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
新知探究
小归纳
由此得到:
相似三角形对应高的比等于相似比.
类似的,我们可以得到其余两组对应边上的高的比也等于相似比.
新知探究
练一练
ΔABC∽ ΔA1B1C1 ,BD和B1D1是它们的中线,
已知 ,B1D1 =4cm,则BD= cm.
6
2.ΔABC∽ ΔA1B1C1, AD和A1D1是对应角平分
线,已知AD=8cm, A1D1=3cm ,则 ΔABC与
ΔA1B1C1的对应高之比为 .
8:3
新知探究
2.相似三角形对应角平分线的比、
对应中线的比都等于相似比
问题:把上图中的高改为中线、角平分线,那么它们对应中线的比,对应角平分线的比等于多少?
图中△ABC和△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的角平分线,那么它们之间有什么关系呢?
A
B
C
D
E
A'
B'
D'
C'
E'
新知探究
已知:△ABC∽△A′B′C′,相似比为k,
求证:
证明:∵ △ABC∽△A′B′C′.
∴ ∠B′= ∠B, .
又AD, AD′分别为对应边的中线.
∴ △ABD∽△A′B′D′.
A'
B'
D'
C'
E'
A
B
C
D
E
新知探究
小归纳
由此得到:
相似三角形对应角平分线的比和对应的中线的比也等于相似比.
类似地,可以得到另外两组对应角平分线和对应中线的比也等于相似比.
新知探究
练一练
3.两个相似三角形的两条对应边的长分别是6cm和8cm,如果它们对应的两条角平分线的和为42cm,那么这两条角平分线的长分别是多少?
解:设较短的角平分线长为xcm,
则由相似性质有 .
解得x=18.
较长的角平分线长为24cm.
故这两条角平分线的长分别为18cm,24cm.
新知探究
思考:通过前面的学习我们知道,如果两个三角形相似,它们对应高的比、对应中线的比和对应角平分线的比都等于相似比.那么它们周长的比之间有什么关系?也等于相似比吗?面积之比呢?
A
B
C
A1
B1
C1
3.相似三角形的周长比等于相似比
新知探究
3.相似三角形的周长比等于相似比
思考:图中(1)(2)(3)分别是边长为1,2,3的等边三角形,它们都相似吗?
(1)
(2)
(3)
1
2
3
(1)与(2)的相似比=______,
(1)与(2)的周长比=______,
(1)与(3)的相似比=______,
(1)与(3)的周长比=______.
1∶ 2
结论: 相似三角形的周长比等于相似比。
(都相似)
1∶ 3
1∶ 2
1∶ 3
新知探究
想一想
证明:设△ABC∽△A1B1C1,相似比为k
求证:相似三角形的周长比等于相似比.
A
B
C
A1
B1
C1
思考:怎么证明这一结论呢?
有
相似三角形周长的比等于相似比.
新知探究
解:设△ABC∽△A′B′C′,相似比为k,
分别作出△ABC和△A′B′C′的高AD和A′D′.
∵△ABC和△A′B′C′都是直角三角形,并且∠B=∠B′,
∴△ABD∽△A′B′D′.
A
B
C
A′
B′
C′
D
D′
思考:如果两个相似三角形的相似比为k ,
那么面积比是什么呢?
∵△ABC∽△A′B′C′.
4.相似三角形的面积比等于相似比的平方
∴
新知探究
小归纳
相似三角形的面积比等于相似比的平方.
新知探究
练一练
4.已知ΔABC与ΔA′B′C′的相似比为2:3,则对
应边上中线之比 ,面积之比为 .
4. 如果两个相似三角形的面积之比为1:9,
周长的比为______ .
1:3
2:3
4:9
03 典型例题
3.两个相似三角形对应中线的比为 ,
则对应高的比为______ .
2.相似三角形对应边的比为2∶3,那么对应角的角平分线的比为______.
2∶ 3
1.两个相似三角形的相似比为 , 则对应高的比为_________, 则对应中线的比为_________.
典型例题
解:∵ △ABC∽△DEF,
解得,EH=3.2(cm).
答:EH的长为3.2cm.
A
G
B
C
D
E
F
H
4.已知△ABC∽△DEF,BG、EH分△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
典型例题
5. 如图,是一个照相机成像的示意图.
(1)如果像高MN是35mm,焦距是50mm,拍摄的景物高度AB是4.9m,拍摄点离景物由多远?
解:(1)根据物体成像原理知:△LMN ∽△LBA,
∴ ,
∵ 像高MN为35mm,焦距是50mm,
拍摄的景物高度AB是4.9m,
∴ ,解得LD=7,∴拍摄点距景物7m
典型例题
(2)拍摄高度是2m的景物,拍摄点离景物有4m,像高不变
∴ ,解得LC=70
∴ 相机的焦距应调整为70mm
典型例题
(2)如果要完整的拍摄高度是2m的景物,拍摄点离景物有4m,像高不变,则相机的焦距应调整为多少毫米?
04 拓展提高
拓展提高
如图,△ABC 中,DE∥BC,DE 分别交 AB、AC 于
点 D、E,S△ADE=2 S△DCE,求 S△ADE ∶S△ABC.
解:过点 D 作 AC 的垂线,交点为 F,则
∴
又∵ DE∥BC,
∴ △ADE ∽△ABC.
A
B
C
D
E
F
拓展提高
∴
即 S△ADE : S△ABC =4 : 9.
05 课堂小结
课堂小结
相似三角形的性质1
相似三角形对应高的比等于相似比
相似三角形对应角平分线的比等于相似比
相似三角形对应中线的比等于相似比
课堂小结
相似三角形的性质2
相似三角形周长之比等于相似比
相似三角形面积之比等于相似比的平方
06 作业布置
1、完成课本习题 3.4 A、B组
2、熟记相似三角形的性质,熟练的掌握周长、面积与相似比之间的关系。
作业布置
谢 谢 观 看
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
