湘教版九年级数学上册第3章 图形的相似3.5 相似三角形的应用教学课件(共27张)
文档属性
| 名称 | 湘教版九年级数学上册第3章 图形的相似3.5 相似三角形的应用教学课件(共27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-16 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
相似三角形的应用
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
胡夫金字塔是埃及现存规模最大的金字塔,被誉为“世界古代八大奇迹之一”,古希腊数学家,天文学家泰勒斯曾经利用相似三角形的原理测量金字塔的高度.
同学们想知道泰勒斯是怎么求出胡夫金字塔的高度的吗?我们能否根据之前学过的三角形的相似求出胡夫金字塔的高度吗?
新知探究
相似三角形的应用
台湾最高的楼
——台北101大楼
怎样测量这些非常高大的物体的高度?
02 新知探究
新知探究
1.利用相似三角形判定宽度
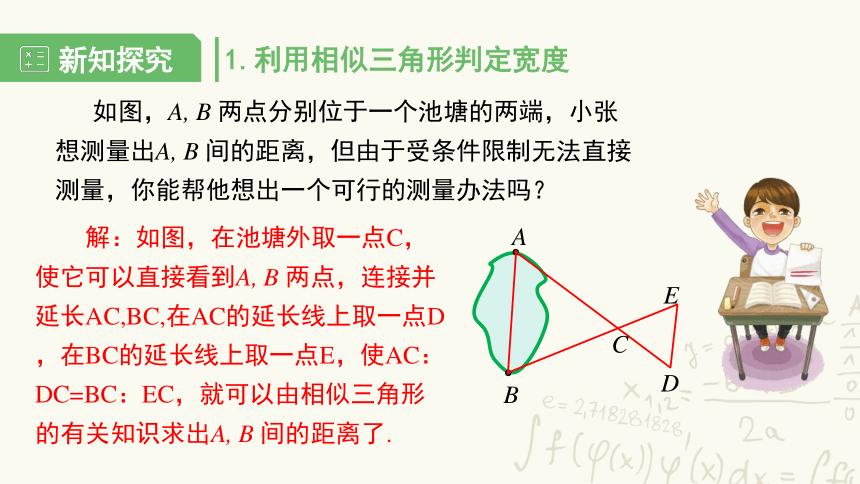
如图,A, B 两点分别位于一个池塘的两端,小张想测量出A, B 间的距离,但由于受条件限制无法直接测量,你能帮他想出一个可行的测量办法吗?
A
B
解:如图,在池塘外取一点C,使它可以直接看到A, B 两点,连接并延长AC,BC,在AC的延长线上取一点D,在BC的延长线上取一点E,使AC:DC=BC:EC,就可以由相似三角形的有关知识求出A, B 间的距离了.
C
D
E
新知探究
如果=2,且测得DE的长为50m,则A,B两点间的距离为多少?
1.利用相似三角形判定宽度
解: =2,∠ACB=∠DCE
∴△ABC∽△DEC
∴ 2
∵DE=50m,
∴AB=2DE=100m
新知探究
表达式:物1高 :物2高 = 影1长 :影2长
测高方法一:
测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决.
2.利用相似三角形测量高度
新知探究
解:物1高 :物2高 = 影1长 :影2长
同一时刻,一竿高为2m,影长为1.2m,某塔的影长为18m,则塔高为________.
练一练
∴2:塔高=1.2:18
求得塔高=30m
30m
新知探究
测高方法二:
测量不能到达顶部的物体的高度,也可以用“利用镜子的反射测量高度”的原理解决.
2.利用相似三角形测量高度
OB
EF
=
OA
AF
△ABO∽△AEF
OB =
A
F
E
B
O
┐
┐
平面镜
OA · EF
AF
新知探究
练一练
如图是小明设计用手电来测量某古城墙高度的示意图,点 P 处放一水平的平面镜,光线从点 A出发经平面镜反射后,刚好射到古城墙的顶端 C 处,已知 AB = 2 米,且测得 BP = 3 米,DP = 12 米,那么该古城墙的高度是 ( )
A. 6米 B. 8米 C. 18米 D. 24米
B
新知探究
3.利用相似解决有遮挡问题
如图,左、右并排的两棵大树的高分别是 AB = 8 m 和 CD = 12 m,两树底部的距离 BD = 5 m,一个人估计自己眼睛距离地面 1.6 m,她沿着正对这两棵树的一条水平直路 l 从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C 了?
解:如图,假设观察者从左向右走到点 E 时,她的眼睛的位置点 E 与两棵树的顶端点 A,C 恰在一条 直线上.
∵AB⊥l,CD⊥l,∴AB∥CD.
∴△AEH∽△CEK.
∴ ,
即
解得 EH=8.
由此可知,如果观察者继续前进,当她与左边的树的距离小于 8 m 时,由于这棵树的遮挡,就看不到右边树的顶端 C .
3.利用相似解决有遮挡问题
新知探究
03 典型例题
1. 小明身高 1.5 米,在操场的影长为 2 米,同时测得
教学大楼在操场的影长为 60 米,则教学大楼的高
度应为 ( )
A. 45米 B. 40米 C. 90米 D. 80米
2. 小刚身高 1.7 m,测得他站立在阳光下的影子长为
0.85 m,紧接着他把手臂竖直举起,测得影子长
为 1.1 m,那么小刚举起的手臂超出头顶 ( )
A. 0.5m B. 0.55m C. 0.6m D . 2.2m
A
A
典型例题
3. 如图,九年级某班数学兴趣小组的同学想利用所学数学知识测量学校旗杆的高度,当身高 1.6 米的楚阳同学站在 C 处时,他头顶端的影子正好与旗杆顶端的影子重合,同一时刻,其他成员测得 AC = 2 米,AB = 10 米,则旗杆的高度是______米.
8
典型例题
4.如图,小明为了测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m,求树的高度.
分析:人、树、标杆是相互平行的,添加辅助线,过点A作AN∥BD交ID于N,交EF于M,则可△AEM∽△ACN.
A
E
C
D
F
B
N
典型例题
A
E
C
D
F
B
N
解:过点A作AN∥BD交CD于N,交EF于M,因为人、标杆、树都垂直于地面,
∴∠ABF=∠EFD=∠CDF=90°,
∴AB∥EF∥CD, ∴∠EMA=∠CNA.
∵∠EAM=∠CAN,
∴△AEM∽△ACN ,
∴ .
∵AB=1.6m , EF=2m , BD=27m , FD=24m ,
∴ , ∴CN=3.6(m),
∴CD=3.6+1.6=5.2(m).
故树的高度为5.2m.
典型例题
04 拓展提高
拓展提高
如图,某校数学兴趣小组利用自制的直角三角形硬纸板 DEF 来测量操场旗杆 AB 的高度,他们通过调整测量位置,使斜边 DF 与地面保持平行,并使边DE 与旗杆顶点 A 在同一直线上,已知 DE = 0.5 米,EF = 0.25 米,目测点 D 到地面的距离 DG = 1.5 米,到旗杆的水平距离 DC = 20 米,求旗杆的高度.
A
B
C
D
G
E
F
拓展提高
A
B
C
D
G
E
F
解:由题意可得:△DEF∽△DCA,
∵DE=0.5米,EF=0.25米,DG=1.5米,DC=20米,
则
解得:AC = 10,
故 AB = AC + BC
= 10 + 1.5 = 11.5 (m).
答:旗杆的高度为 11.5 m.
∴
05 课堂小结
课堂小结
相似三角形的应用举例
利用相似三角形测量高度
利用相似三角形测量宽度
利用相似解决有遮挡物问题
06 作业布置
完成课本习题 3.5 A、B组
作业布置
谢 谢 观 看
相似三角形的应用
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
胡夫金字塔是埃及现存规模最大的金字塔,被誉为“世界古代八大奇迹之一”,古希腊数学家,天文学家泰勒斯曾经利用相似三角形的原理测量金字塔的高度.
同学们想知道泰勒斯是怎么求出胡夫金字塔的高度的吗?我们能否根据之前学过的三角形的相似求出胡夫金字塔的高度吗?
新知探究
相似三角形的应用
台湾最高的楼
——台北101大楼
怎样测量这些非常高大的物体的高度?
02 新知探究
新知探究
1.利用相似三角形判定宽度
如图,A, B 两点分别位于一个池塘的两端,小张想测量出A, B 间的距离,但由于受条件限制无法直接测量,你能帮他想出一个可行的测量办法吗?
A
B
解:如图,在池塘外取一点C,使它可以直接看到A, B 两点,连接并延长AC,BC,在AC的延长线上取一点D,在BC的延长线上取一点E,使AC:DC=BC:EC,就可以由相似三角形的有关知识求出A, B 间的距离了.
C
D
E
新知探究
如果=2,且测得DE的长为50m,则A,B两点间的距离为多少?
1.利用相似三角形判定宽度
解: =2,∠ACB=∠DCE
∴△ABC∽△DEC
∴ 2
∵DE=50m,
∴AB=2DE=100m
新知探究
表达式:物1高 :物2高 = 影1长 :影2长
测高方法一:
测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决.
2.利用相似三角形测量高度
新知探究
解:物1高 :物2高 = 影1长 :影2长
同一时刻,一竿高为2m,影长为1.2m,某塔的影长为18m,则塔高为________.
练一练
∴2:塔高=1.2:18
求得塔高=30m
30m
新知探究
测高方法二:
测量不能到达顶部的物体的高度,也可以用“利用镜子的反射测量高度”的原理解决.
2.利用相似三角形测量高度
OB
EF
=
OA
AF
△ABO∽△AEF
OB =
A
F
E
B
O
┐
┐
平面镜
OA · EF
AF
新知探究
练一练
如图是小明设计用手电来测量某古城墙高度的示意图,点 P 处放一水平的平面镜,光线从点 A出发经平面镜反射后,刚好射到古城墙的顶端 C 处,已知 AB = 2 米,且测得 BP = 3 米,DP = 12 米,那么该古城墙的高度是 ( )
A. 6米 B. 8米 C. 18米 D. 24米
B
新知探究
3.利用相似解决有遮挡问题
如图,左、右并排的两棵大树的高分别是 AB = 8 m 和 CD = 12 m,两树底部的距离 BD = 5 m,一个人估计自己眼睛距离地面 1.6 m,她沿着正对这两棵树的一条水平直路 l 从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C 了?
解:如图,假设观察者从左向右走到点 E 时,她的眼睛的位置点 E 与两棵树的顶端点 A,C 恰在一条 直线上.
∵AB⊥l,CD⊥l,∴AB∥CD.
∴△AEH∽△CEK.
∴ ,
即
解得 EH=8.
由此可知,如果观察者继续前进,当她与左边的树的距离小于 8 m 时,由于这棵树的遮挡,就看不到右边树的顶端 C .
3.利用相似解决有遮挡问题
新知探究
03 典型例题
1. 小明身高 1.5 米,在操场的影长为 2 米,同时测得
教学大楼在操场的影长为 60 米,则教学大楼的高
度应为 ( )
A. 45米 B. 40米 C. 90米 D. 80米
2. 小刚身高 1.7 m,测得他站立在阳光下的影子长为
0.85 m,紧接着他把手臂竖直举起,测得影子长
为 1.1 m,那么小刚举起的手臂超出头顶 ( )
A. 0.5m B. 0.55m C. 0.6m D . 2.2m
A
A
典型例题
3. 如图,九年级某班数学兴趣小组的同学想利用所学数学知识测量学校旗杆的高度,当身高 1.6 米的楚阳同学站在 C 处时,他头顶端的影子正好与旗杆顶端的影子重合,同一时刻,其他成员测得 AC = 2 米,AB = 10 米,则旗杆的高度是______米.
8
典型例题
4.如图,小明为了测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m,求树的高度.
分析:人、树、标杆是相互平行的,添加辅助线,过点A作AN∥BD交ID于N,交EF于M,则可△AEM∽△ACN.
A
E
C
D
F
B
N
典型例题
A
E
C
D
F
B
N
解:过点A作AN∥BD交CD于N,交EF于M,因为人、标杆、树都垂直于地面,
∴∠ABF=∠EFD=∠CDF=90°,
∴AB∥EF∥CD, ∴∠EMA=∠CNA.
∵∠EAM=∠CAN,
∴△AEM∽△ACN ,
∴ .
∵AB=1.6m , EF=2m , BD=27m , FD=24m ,
∴ , ∴CN=3.6(m),
∴CD=3.6+1.6=5.2(m).
故树的高度为5.2m.
典型例题
04 拓展提高
拓展提高
如图,某校数学兴趣小组利用自制的直角三角形硬纸板 DEF 来测量操场旗杆 AB 的高度,他们通过调整测量位置,使斜边 DF 与地面保持平行,并使边DE 与旗杆顶点 A 在同一直线上,已知 DE = 0.5 米,EF = 0.25 米,目测点 D 到地面的距离 DG = 1.5 米,到旗杆的水平距离 DC = 20 米,求旗杆的高度.
A
B
C
D
G
E
F
拓展提高
A
B
C
D
G
E
F
解:由题意可得:△DEF∽△DCA,
∵DE=0.5米,EF=0.25米,DG=1.5米,DC=20米,
则
解得:AC = 10,
故 AB = AC + BC
= 10 + 1.5 = 11.5 (m).
答:旗杆的高度为 11.5 m.
∴
05 课堂小结
课堂小结
相似三角形的应用举例
利用相似三角形测量高度
利用相似三角形测量宽度
利用相似解决有遮挡物问题
06 作业布置
完成课本习题 3.5 A、B组
作业布置
谢 谢 观 看
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
