高中数学北师大版必修1学案:第1章集合章末复习课
文档属性
| 名称 | 高中数学北师大版必修1学案:第1章集合章末复习课 |
|
|
| 格式 | zip | ||
| 文件大小 | 379.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-16 23:34:37 | ||
图片预览


文档简介
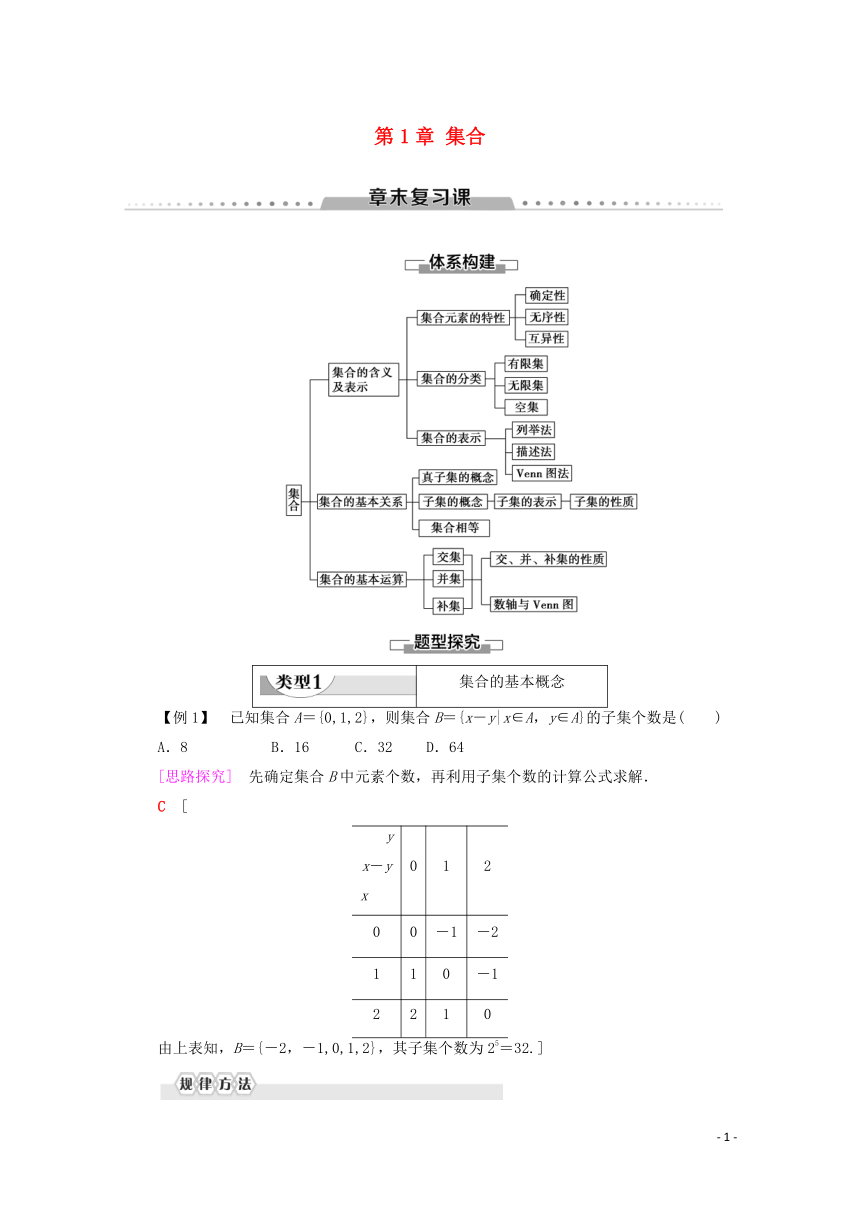
第1章 集合
集合的基本概念
【例1】 已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}的子集个数是( )
A.8 B.16 C.32 D.64
[思路探究] 先确定集合B中元素个数,再利用子集个数的计算公式求解.
C [
y
x-y
x
0
1
2
0
0
-1
-2
1
1
0
-1
2
2
1
0
由上表知,B={-2,-1,0,1,2},其子集个数为25=32.]
1.用列举法表示集合,其默认的条件是集合中的元素各不相同,也就是说集合中的元素一定要满足互异性.
2.判断集合中元素个数时,要注意相同的对象归入同一个集合时只能算作一个.
3.若集合中的元素含有参数,要抓住集合中元素的互异性,采用分类讨论的方法进行研究.
1.若集合A={x∈R|ax2+ax+1=0}中只有一个元素,则a=( )
A.4 B.2 C.0 D.0或4
A [当a=0时,A=?,不合题意;当a≠0时,Δ=a2-4a=0,解得a=4.]
2.若2∈{2a-1,1-a2},则a=________.
[∵1-a2≤1,∴2a-1=2,解得a=.]
集合的基本关系
【例2】 已知集合A={x|x>0,x∈R},B={x|x2-x+p=0},且B?A,求实数p的取值范围.
[解] (1)当B=?时,B?A,由Δ=(-1)2-4p<0,
解得p>.
(2)当B≠?,且B?A时,方程x2-x+p=0存在两个正实根.
由x1+x2=1>0,Δ=(-1)2-4p≥0,且x1x2=p>0,
得0由(1)(2)可得p的取值范围为{p|p>0}.
1.判断两集合关系的两种常用方法
一是化集合,从表达式中寻找两集合间的关系;二是用列举法表示各集合,从元素中寻找关系.
2.处理集合间关系问题的关键点
已知两集合间的关系求参数时,关键是将两集合间的关系转化为元素间的关系,进而转化为参数满足的关系.解决这类问题常常需要合理利用数轴、Venn图帮助分析.
3.已知集合A={x∈R|-20},则A与B之间的关系为( )
A.AB B.AB C.A=B D.AB
A [B={x|x>-3},
把集合A,B在数轴上表示出来
由上图知,AB.]
4.已知{x|x2-5x+6=0}?{a,2,2a-1},求实数a的值.
[解] 由{x|x2-5x+6=0}={2,3},得3∈{a,2,2a-1},
∴a=3,或2a-1=3,
解得a=2或3.
当a=2时,集合{a,2,2a-1}中的元素不满足互异性,舍去.
当a=3时,{a,2,2a-1}={3,2,5}满足题意.
综上得,a=3.
集合的基本运算
设集合A={x|-1≤x≤6},B={x|m-1≤x≤2m+1},已知A∪B=A,求实数m的取值范围.
[思路探究] 由A∪B=A知B?A,需按B=?与B≠?两种情况讨论,当B≠?时,利用数轴列出关于m的不等式组求得m的取值范围.
[解] ∵A∪B=A,∴B?A.
当m-1>2m+1,即m<-2时,B=?,符合题意.
当m-1≤2m+1,即m≥-2时,B≠?.
由B?A,借助数轴表示如图所示.
则解得0≤m≤.
综上所述,实数m的取值范围是m<-2或0≤m≤.
在集合运算过程中应力求做到“三化”:
?1?意义化:首先分清集合的类型,是表示数集、点集,还是某类图形;是表示函数自变量的取值范围、因变量的取值范围,还是表示方程或不等式的解集.
?2?具体化:具体求出相关集合中函数的自变量、因变量的范围或方程、不等式的解集等;不能具体求出的,也应力求将相关集合转化为最简形式.
?3?直观化:借助数轴、直角坐标平面、Venn图等将有关集合直观地表示出来,从而借助数形结合思想解决问题.
5.(1)已知集合P={x|x2≤1},M={a}.若P∪M=P,则a的取值范围是( )
A.-1≤a≤1 B.a≥1
C.a≤-1 D.a≥1或a≤-1
(2)若集合A={x||x|≤1,x∈R},B={y|y=x2,x∈R},则A∩B=( )
A.{x|-1≤x≤1} B.{x|x≥0}
C.{x|0≤x≤1} D.?
(3)已知A,B均为集合U={1,3,5,7,9}的子集,且A∩B={3},(?UB)∩A={9},则A=( )
A.{1,3} B.{3,7,9}
C.{3,5,9} D.{3,9}
(4)设全集U={1,2,3,4,5},集合A={1,a2-1,4},?UA={2,a+3},则实数a=________.
(1)A (2)C (3)D (4)2 [(1)由P∪M=P,得M?P,所以a∈P,所以a2≤1,解得-1≤a≤1.
(2)A={x|-1≤x≤1},B={y|y≥0},所以,A∩B={x|0≤x≤1}.
(3)用Venn图求解.
由上图知,A={3,9}.
(4)依题意得
或
解得a=2.]
补集思想的应用
[探究问题]
1.任何一个集合都可以作为全集,对吗?
提示:不对.由全集的定义可知,空集就不能当全集,因为空集不含任何元素.
2.?UA在U中的补集?U(?UA)与集合A有什么关系?
提示:相等.
3.?AC与?BC相等吗?为什么?
提示:不一定.依据补集的含义,符号?AC和?BC都表示集合C的补集,但是?AC表示集合C在全集A中的补集,而?BC表示集合C在全集B中的补集,由于集合A和B不一定相等,所以?AC与?BC不一定相等.因此,求集合的补集时,首先要明确全集,否则容易出错.
如集合A={1,2,3,4,5,6,7,8,9},B={0,1,2,3,4},C={1,3,4},则?AC={2,5,6,7,8,9},?BC={0,2},很明显?AC≠?BC.
若集合A={x|ax2+3x+2=0}中至少有1个元素,求实数a的取值范围.
[思路探究] 从已知的反面出发,求出a的取值范围,再求其补集.
[解] 由A=?,得解得a>,
所以,当A至少有一个元素时,a≤.
补集思想的解题方法,当从正面考虑情况较多,问题较复杂的时候,往往考虑运用补集思想.其解题步骤为:
?1?否定已知条件,考虑反面问题;
?2?求解反面问题对应的参数范围;
?3?取反面问题对应的参数范围的补集.
6.已知集合A={y|y>a2+1,或y[解] 若A∩B=?,则
解得a≤-,或≤a≤2,
所以,当A∩B≠?时,-2.
集合的基本概念
【例1】 已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}的子集个数是( )
A.8 B.16 C.32 D.64
[思路探究] 先确定集合B中元素个数,再利用子集个数的计算公式求解.
C [
y
x-y
x
0
1
2
0
0
-1
-2
1
1
0
-1
2
2
1
0
由上表知,B={-2,-1,0,1,2},其子集个数为25=32.]
1.用列举法表示集合,其默认的条件是集合中的元素各不相同,也就是说集合中的元素一定要满足互异性.
2.判断集合中元素个数时,要注意相同的对象归入同一个集合时只能算作一个.
3.若集合中的元素含有参数,要抓住集合中元素的互异性,采用分类讨论的方法进行研究.
1.若集合A={x∈R|ax2+ax+1=0}中只有一个元素,则a=( )
A.4 B.2 C.0 D.0或4
A [当a=0时,A=?,不合题意;当a≠0时,Δ=a2-4a=0,解得a=4.]
2.若2∈{2a-1,1-a2},则a=________.
[∵1-a2≤1,∴2a-1=2,解得a=.]
集合的基本关系
【例2】 已知集合A={x|x>0,x∈R},B={x|x2-x+p=0},且B?A,求实数p的取值范围.
[解] (1)当B=?时,B?A,由Δ=(-1)2-4p<0,
解得p>.
(2)当B≠?,且B?A时,方程x2-x+p=0存在两个正实根.
由x1+x2=1>0,Δ=(-1)2-4p≥0,且x1x2=p>0,
得0
1.判断两集合关系的两种常用方法
一是化集合,从表达式中寻找两集合间的关系;二是用列举法表示各集合,从元素中寻找关系.
2.处理集合间关系问题的关键点
已知两集合间的关系求参数时,关键是将两集合间的关系转化为元素间的关系,进而转化为参数满足的关系.解决这类问题常常需要合理利用数轴、Venn图帮助分析.
3.已知集合A={x∈R|-2
A.AB B.AB C.A=B D.AB
A [B={x|x>-3},
把集合A,B在数轴上表示出来
由上图知,AB.]
4.已知{x|x2-5x+6=0}?{a,2,2a-1},求实数a的值.
[解] 由{x|x2-5x+6=0}={2,3},得3∈{a,2,2a-1},
∴a=3,或2a-1=3,
解得a=2或3.
当a=2时,集合{a,2,2a-1}中的元素不满足互异性,舍去.
当a=3时,{a,2,2a-1}={3,2,5}满足题意.
综上得,a=3.
集合的基本运算
设集合A={x|-1≤x≤6},B={x|m-1≤x≤2m+1},已知A∪B=A,求实数m的取值范围.
[思路探究] 由A∪B=A知B?A,需按B=?与B≠?两种情况讨论,当B≠?时,利用数轴列出关于m的不等式组求得m的取值范围.
[解] ∵A∪B=A,∴B?A.
当m-1>2m+1,即m<-2时,B=?,符合题意.
当m-1≤2m+1,即m≥-2时,B≠?.
由B?A,借助数轴表示如图所示.
则解得0≤m≤.
综上所述,实数m的取值范围是m<-2或0≤m≤.
在集合运算过程中应力求做到“三化”:
?1?意义化:首先分清集合的类型,是表示数集、点集,还是某类图形;是表示函数自变量的取值范围、因变量的取值范围,还是表示方程或不等式的解集.
?2?具体化:具体求出相关集合中函数的自变量、因变量的范围或方程、不等式的解集等;不能具体求出的,也应力求将相关集合转化为最简形式.
?3?直观化:借助数轴、直角坐标平面、Venn图等将有关集合直观地表示出来,从而借助数形结合思想解决问题.
5.(1)已知集合P={x|x2≤1},M={a}.若P∪M=P,则a的取值范围是( )
A.-1≤a≤1 B.a≥1
C.a≤-1 D.a≥1或a≤-1
(2)若集合A={x||x|≤1,x∈R},B={y|y=x2,x∈R},则A∩B=( )
A.{x|-1≤x≤1} B.{x|x≥0}
C.{x|0≤x≤1} D.?
(3)已知A,B均为集合U={1,3,5,7,9}的子集,且A∩B={3},(?UB)∩A={9},则A=( )
A.{1,3} B.{3,7,9}
C.{3,5,9} D.{3,9}
(4)设全集U={1,2,3,4,5},集合A={1,a2-1,4},?UA={2,a+3},则实数a=________.
(1)A (2)C (3)D (4)2 [(1)由P∪M=P,得M?P,所以a∈P,所以a2≤1,解得-1≤a≤1.
(2)A={x|-1≤x≤1},B={y|y≥0},所以,A∩B={x|0≤x≤1}.
(3)用Venn图求解.
由上图知,A={3,9}.
(4)依题意得
或
解得a=2.]
补集思想的应用
[探究问题]
1.任何一个集合都可以作为全集,对吗?
提示:不对.由全集的定义可知,空集就不能当全集,因为空集不含任何元素.
2.?UA在U中的补集?U(?UA)与集合A有什么关系?
提示:相等.
3.?AC与?BC相等吗?为什么?
提示:不一定.依据补集的含义,符号?AC和?BC都表示集合C的补集,但是?AC表示集合C在全集A中的补集,而?BC表示集合C在全集B中的补集,由于集合A和B不一定相等,所以?AC与?BC不一定相等.因此,求集合的补集时,首先要明确全集,否则容易出错.
如集合A={1,2,3,4,5,6,7,8,9},B={0,1,2,3,4},C={1,3,4},则?AC={2,5,6,7,8,9},?BC={0,2},很明显?AC≠?BC.
若集合A={x|ax2+3x+2=0}中至少有1个元素,求实数a的取值范围.
[思路探究] 从已知的反面出发,求出a的取值范围,再求其补集.
[解] 由A=?,得解得a>,
所以,当A至少有一个元素时,a≤.
补集思想的解题方法,当从正面考虑情况较多,问题较复杂的时候,往往考虑运用补集思想.其解题步骤为:
?1?否定已知条件,考虑反面问题;
?2?求解反面问题对应的参数范围;
?3?取反面问题对应的参数范围的补集.
6.已知集合A={y|y>a2+1,或y
解得a≤-,或≤a≤2,
所以,当A∩B≠?时,-
