高中数学北师大版必修1学案:第2章函数1生活中的变量关系2对函数的进一步认识2.2函数的表示法
文档属性
| 名称 | 高中数学北师大版必修1学案:第2章函数1生活中的变量关系2对函数的进一步认识2.2函数的表示法 |

|
|
| 格式 | zip | ||
| 文件大小 | 452.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-16 23:24:55 | ||
图片预览




文档简介
2.2 函数的表示法
学 习 目 标
核 心 素 养
1.掌握函数的三种表示方法.(重点)
2.会根据不同的需要选择恰当的方法表示函数.(难点)
3.了解简单的分段函数,并能简单应用.(重点、难点)
1.通过应用函数的表示方法提升数学抽象素养.
2.通过分段函数的简单应用提升数学运算素养.
1.函数的表示法
阅读教材P28~P29“例2”以上内容,完成下列问题.
函数的三种表示方法
表示法
定义
解析法
用自变量的解析表达式表示两个变量之间的对应关系
图像法
用图像表示两个变量之间的对应关系
列表法
列出表格来表示两个变量之间的对应关系
思考1:函数的三种表示方法各有什么优、缺点?
[提示] 三种表示方法的优、缺点比较:
优点
缺点
解析法
①简明、全面地概括了变量间的关系;②可以通过解析式求出任意一个自变量所对应的函数值
不够形象、直观
列表法
不通过计算就可以直接看出与自变量的值相对应的函数值
一般只能表示部分自变量的函数值
图像法
直观、形象地表示出函数的变化情况,有利于通过图形研究函数的某些性质
只能近似地求出自变量所对应的函数值,有时误差较大
思考2:任何一个函数是不是都可以用解析法、列表法、图像法三种形式来表示.
[提示] 并不是所有的函数都可以用解析式表示,例如人的心跳强度与时间的函数关系.图像法也不适用于所有函数,例如D(x)=对于函数值有无限个的情况,无法用列表法表示.
2.分段函数
阅读教材P29“例2”~P31,完成下列问题.
在函数的定义域内,对于自变量x的不同取值,对应关系也不同,这样的函数通常称为分段函数.
思考3:如何求分段函数的值域?
[提示] 先求出每一段中函数值的取值范围,再求其并集.
1.已知函数f(x)由下表给出,则f(3)=( )
x
1≤x<2
2
2f(x)
1
2
3
A.1 B.2 C.3 D.不存在
C [因为3∈(2,4],所以f(3)=3.]
2.函数f(x)的图像如图所示,则f(x)的定义域是______,值域是______.
[-1,2) (-1,1] [观察图像,得f(x)的定义域为:[-1,2).值域为:(-1,1].]
3.已知f(x)是一次函数,且其图像过点A(-2,0),B(1,5),则f(x)的解析式为________.
f(x)=x+ [设f(x)=kx+b,依题意,得
解得所以,f(x)=x+.]
4.函数f(x),g(x)分别由下表给出
x
1
2
3
f(x)
1
3
1
x
1
2
3
g(x)
3
2
1
则f(g(2))的值为________.
3 [因为g(2)=2,f(2)=3,所以f(g(2))=3.]
函数图像的作法
【例1】 作出下列函数的图像并求出其值域.
(1)y=2x+1,x∈[0,2];
(2)y=,x∈[2,+∞);
(3)y=x2+2x,x∈[-2,2].
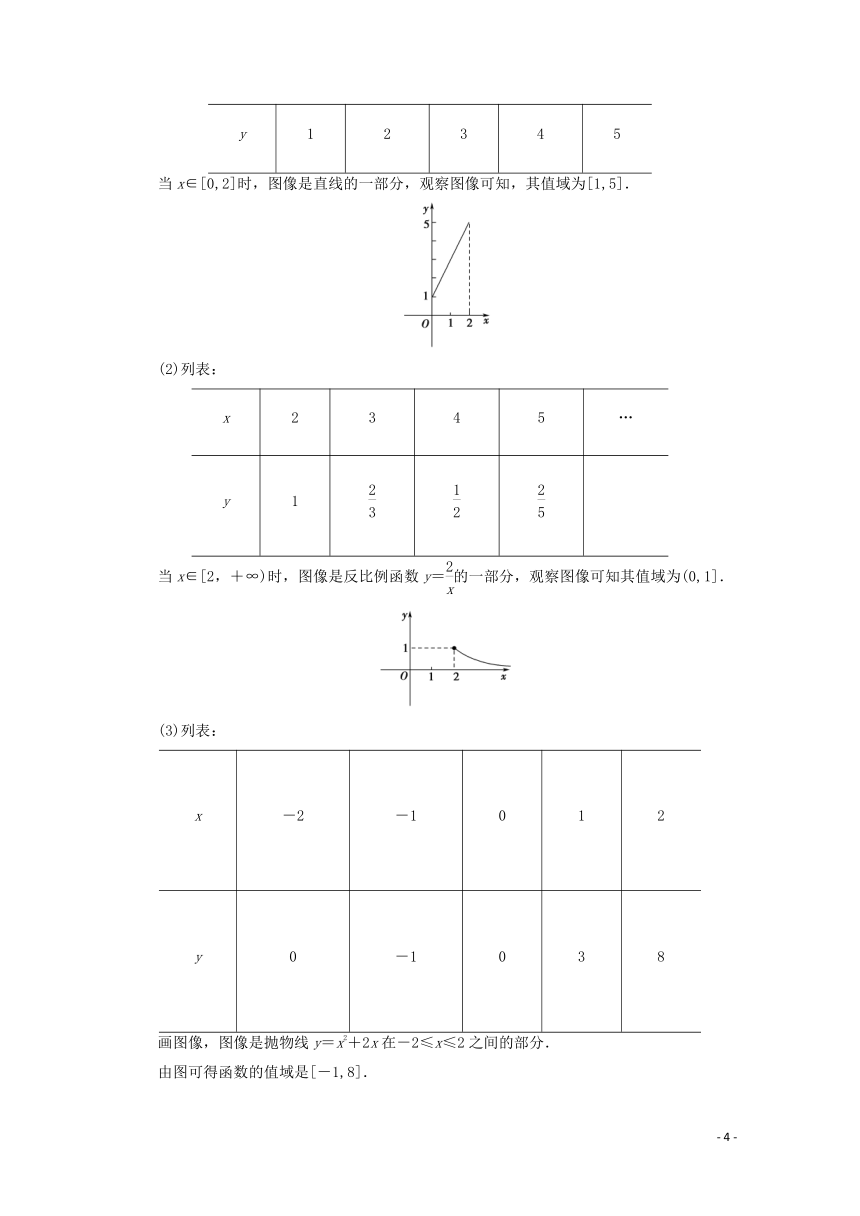
[解] (1)列表:
x
0
1
2
y
1
2
3
4
5
当x∈[0,2]时,图像是直线的一部分,观察图像可知,其值域为[1,5].
(2)列表:
x
2
3
4
5
…
y
1
当x∈[2,+∞)时,图像是反比例函数y=的一部分,观察图像可知其值域为(0,1].
(3)列表:
x
-2
-1
0
1
2
y
0
-1
0
3
8
画图像,图像是抛物线y=x2+2x在-2≤x≤2之间的部分.
由图可得函数的值域是[-1,8].
1.作函数图像主要有三步:列表、描点、连线.作图像时一般应先确定函数的定义域,再在定义域内化简函数解析式,再列表画出图像.
2.函数的图像可能是平滑的曲线,也可能是一群孤立的点,画图时要注意关键点,如图像与坐标轴的交点、区间端点、二次函数的顶点等等,还要分清这些关键点是实心点还是空心点.
1.作出下列函数的图像.
(1)y=x+1(x≤0);
(2)y=x2-2x(x>1,或x<-1).
[解] (1)y=x+1(x≤0)表示一条射线,图像如图①.
(2)y=x2-2x=(x-1)2-1(x>1,或x<-1)是抛物线y=x2-2x去掉-1≤x≤1之间的部分后剩余的曲线.如图②.
求函数的解析式
【例2】 (1)若f(x+1)=x2+x,则f(x)=________.
(2)若f(x)是一次函数,且f(f(x))=4x-1,则f(x)=________.
(3)已知函数y=f(x)满足2f(x)+f=2x(x∈R且x≠0),则f(x)=________.
(1)x2-x (2)2x-或-2x+1
(3)x- [(1)因为x∈R,
所以令t=x+1∈R,则x=t-1,
代入f(x+1)=x2+x,
得f(t)=(t-1)2+(t-1)=t2-t,t∈R,
即f(x)=x2-x.
(2)由f(x)是一次函数,设f(x)=ax+b(a≠0),
则f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b=4x-1,
所以
解得或
所以f(x)=2x-或f(x)=-2x+1.
(3)由2f(x)+f=2x, ①
将x换成,则换成x,
得2f+f(x)=, ②
①×2-②,得3f(x)=4x-,
所以f(x)=x-.]
求函数解析式的常用方法
?1?待定系数法:若已知函数的类型,可用待定系数法求解,即由函数类型设出函数解析式,再根据条件列方程?组?,通过解方程?组?求出待定系数,进而求出函数解析式.
?2?换元法?有时可用“配凑法”?:已知函数f[g?x?]的解析式求f?x?的解析式,可用换元法?或“配凑法”?,即令g?x?=t,反解出x,然后代入f[g?x?]中求出f?t?,从而求出f?x?.
?3?消元法?或解方程组法?:在已知式子中,含有关于两个不同变量的函数,而这两个变量有着某种关系,这时就要依据两个变量的关系,建立一个新的关于这两个变量的式子,由两个式子建立方程组,通过解方程组消去一个变量,得到目标变量的解析式,这种方法叫做消元法?或解方程组法?.
2.(1)设函数g(x)=2x-1,则g(x+2)=( )
A.2x+1 B.2x-1
C.2x+3 D.2x-3
(2)设f(x)=2x-3,g(x+2)=f(x),则g(x)=( )
A.2x+1 B.2x+3
C.2x-7 D.2x-3
(1)C (2)C [(1)因为g(x)=2x-1,所以g(x+2)=2(x+2)-1=2x+3.
(2)g(x+2)=f(x)=2x-3,令t=x+2,则x=t-2.
所以g(t)=2(t-2)-3=2t-7,即g(x)=2x-7.]
分段函数及应用
[探究问题]
1.已知函数f(x)=3|x-1|-2.
(1)把函数f(x)写成分段的形式;
(2)画出函数f(x)的图像;
(3)观察f(x)的图像,它是轴对称图形吗?若是,它的对称轴是什么?
(4)如何由函数g(x)=3|x|的图像得到f(x)=3|x-1|-2的图像?
提示:(1)f(x)=
(2)分段画函数图像:
(3)f(x)的图像是轴对称图形,其对称轴为直线x=1.
(4)把函数y=3|x|的图像向右平移1个单位长度,再向下平移2个单位长度可得到函数y=3|x-1|-2的图像.
2.设函数f(x)=
(1)求f与f;
(2)若f(x0)=4,求实数x0的值.
提示:(1)f=-=,f=2=.
(2)由f(x0)=4,
得或
解得x0=-4或2.
3.对于探究2中的函数,探究以下问题.
(1)若f(x)≤,求x的取值范围;
(2)求函数f(x)的值域.
提示:(1)由f(x)≤,
得或
解得-≤x≤0,或0所以,x的取值范围是.
(2)当x≤0时,f(x)≥0;当x>0时,f(x)>0,
所以,f(x)的值域为[0,+∞)∪(0,+∞)=[0,+∞).
【例3】 已知f(x)=
(1)求f{f[f(5)]}的值;
(2)画出该函数的图像;
(3)根据所画图像,写出函数的定义域,值域.
[思路探究] (1)从里向外依次求值,每一次求值时,应先判断自变量的取值属于哪一段,再利用该段的解析式求值;(2)分段画函数图像;(3)观察函数图像写出定义域,值域.
[解] (1)f{f[f(5)]}=f[f(-3)]=f(1)=-1.
(2)
(3)定义域为(-∞,0]∪(0,4]∪(4,+∞)=R,值域为(-∞,4]∪[-1,8]∪(-∞,-2)=R.
1.分段函数求值,一定要注意所给自变量的值所在的范围,代入相应的解析式求得.
2.多层“f”的问题,要按照“由里到外”的顺序,层层处理.
3.已知分段函数的函数值求相对应的自变量的值,可分段利用函数解析式求得自变量的值,但应注意检验分段解析式的适用范围,也可先判断每一段上的函数值的范围,确定解析式再求解.
4.研究分段函数的性质时,应根据“先分后合”的原则,尤其是在作分段函数的图像时,可先将各段的图像分别画出来,再将它们连在一起得到整个函数的图像.
3.(1)函数f(x)=则f(2)=( )
A.-1 B.0
C.1 D.2
(2)已知f(x)=若f(x)>2,求x的取值范围.
(1)A [f(2)=f(2-1)=f(1)=1-2=-1.]
(2)解:当x≥-2时,f(x)=x+2,
由f(x)>2,得x+2>2,
解得x>0,故x>0;
当x<-2时,f(x)=-x-2,
由f(x)>2,得-x-2>2,
解得x<-4,故x<-4.
综上可得:x>0或x<-4.
1.函数三种表示法的优缺点
2.理解分段函数应注意的问题
(1)分段函数是一个函数,其定义域是各段“定义域”的并集,其值域是各段“值域”的并集.写定义域时,区间的端点需不重不漏.
(2)求分段函数的函数值时,自变量的取值属于哪一段,就用哪一段的解析式.
(3)研究分段函数时,应根据“先分后合”的原则,尤其是作分段函数的图像时,可先将各段的图像分别画出来,从而得到整个函数的图像.
3.求函数解析式常用的方法有:(1)待定系数法;(2)换元法;(3)配凑法;(4)消元法等.
1.思考辨析
(1)任何一个函数都可以用解析法表示.( )
(2)y=是分段函数.( )
(3)函数y=的值域是[0,+∞).( )
[答案] (1)× (2)× (3)√
2.已知f(x2-1)=x4-x2+1,则f(x)=________.
x2+x+1(x≥-1) [因为f(x2-1)=x4-x2+1=(x2-1)2+(x2-1)+1,所以f(x)=x2+x+1(x≥-1).]
3.如图,函数f(x)的图像是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),那么f的值等于________.
2 [由函数f(x)图像,知f(1)=2,f(3)=1,
∴f=f(1)=2.]
4.已知函数y=|x-1|+|x+2|.
(1)作出函数的图像;
(2)写出函数的值域;
(3)判断方程|x-1|+|x+2|=4有多少个实数解?
[解] (1)首先考虑去掉解析式中的绝对值符号,第一个绝对值的分段点x=1,第二个绝对值的分段点x=-2,这样数轴被分为三部分:(-∞,-2],(-2,1],(1,+∞).
所以已知函数可写成分段函数形式:
y=|x-1|+|x+2|=
在相应的x取值范围内,分别作出相应函数的图像,如图所示,即为所求函数的图像.
(2)根据函数的图像可知:值域为[3,+∞).
(3)由于直线y=4与函数y=|x-1|+|x+2|的图像有2个交点,所以,方程|x-1|+|x+2|=4有2个实数解.
学 习 目 标
核 心 素 养
1.掌握函数的三种表示方法.(重点)
2.会根据不同的需要选择恰当的方法表示函数.(难点)
3.了解简单的分段函数,并能简单应用.(重点、难点)
1.通过应用函数的表示方法提升数学抽象素养.
2.通过分段函数的简单应用提升数学运算素养.
1.函数的表示法
阅读教材P28~P29“例2”以上内容,完成下列问题.
函数的三种表示方法
表示法
定义
解析法
用自变量的解析表达式表示两个变量之间的对应关系
图像法
用图像表示两个变量之间的对应关系
列表法
列出表格来表示两个变量之间的对应关系
思考1:函数的三种表示方法各有什么优、缺点?
[提示] 三种表示方法的优、缺点比较:
优点
缺点
解析法
①简明、全面地概括了变量间的关系;②可以通过解析式求出任意一个自变量所对应的函数值
不够形象、直观
列表法
不通过计算就可以直接看出与自变量的值相对应的函数值
一般只能表示部分自变量的函数值
图像法
直观、形象地表示出函数的变化情况,有利于通过图形研究函数的某些性质
只能近似地求出自变量所对应的函数值,有时误差较大
思考2:任何一个函数是不是都可以用解析法、列表法、图像法三种形式来表示.
[提示] 并不是所有的函数都可以用解析式表示,例如人的心跳强度与时间的函数关系.图像法也不适用于所有函数,例如D(x)=对于函数值有无限个的情况,无法用列表法表示.
2.分段函数
阅读教材P29“例2”~P31,完成下列问题.
在函数的定义域内,对于自变量x的不同取值,对应关系也不同,这样的函数通常称为分段函数.
思考3:如何求分段函数的值域?
[提示] 先求出每一段中函数值的取值范围,再求其并集.
1.已知函数f(x)由下表给出,则f(3)=( )
x
1≤x<2
2
2
1
2
3
A.1 B.2 C.3 D.不存在
C [因为3∈(2,4],所以f(3)=3.]
2.函数f(x)的图像如图所示,则f(x)的定义域是______,值域是______.
[-1,2) (-1,1] [观察图像,得f(x)的定义域为:[-1,2).值域为:(-1,1].]
3.已知f(x)是一次函数,且其图像过点A(-2,0),B(1,5),则f(x)的解析式为________.
f(x)=x+ [设f(x)=kx+b,依题意,得
解得所以,f(x)=x+.]
4.函数f(x),g(x)分别由下表给出
x
1
2
3
f(x)
1
3
1
x
1
2
3
g(x)
3
2
1
则f(g(2))的值为________.
3 [因为g(2)=2,f(2)=3,所以f(g(2))=3.]
函数图像的作法
【例1】 作出下列函数的图像并求出其值域.
(1)y=2x+1,x∈[0,2];
(2)y=,x∈[2,+∞);
(3)y=x2+2x,x∈[-2,2].
[解] (1)列表:
x
0
1
2
y
1
2
3
4
5
当x∈[0,2]时,图像是直线的一部分,观察图像可知,其值域为[1,5].
(2)列表:
x
2
3
4
5
…
y
1
当x∈[2,+∞)时,图像是反比例函数y=的一部分,观察图像可知其值域为(0,1].
(3)列表:
x
-2
-1
0
1
2
y
0
-1
0
3
8
画图像,图像是抛物线y=x2+2x在-2≤x≤2之间的部分.
由图可得函数的值域是[-1,8].
1.作函数图像主要有三步:列表、描点、连线.作图像时一般应先确定函数的定义域,再在定义域内化简函数解析式,再列表画出图像.
2.函数的图像可能是平滑的曲线,也可能是一群孤立的点,画图时要注意关键点,如图像与坐标轴的交点、区间端点、二次函数的顶点等等,还要分清这些关键点是实心点还是空心点.
1.作出下列函数的图像.
(1)y=x+1(x≤0);
(2)y=x2-2x(x>1,或x<-1).
[解] (1)y=x+1(x≤0)表示一条射线,图像如图①.
(2)y=x2-2x=(x-1)2-1(x>1,或x<-1)是抛物线y=x2-2x去掉-1≤x≤1之间的部分后剩余的曲线.如图②.
求函数的解析式
【例2】 (1)若f(x+1)=x2+x,则f(x)=________.
(2)若f(x)是一次函数,且f(f(x))=4x-1,则f(x)=________.
(3)已知函数y=f(x)满足2f(x)+f=2x(x∈R且x≠0),则f(x)=________.
(1)x2-x (2)2x-或-2x+1
(3)x- [(1)因为x∈R,
所以令t=x+1∈R,则x=t-1,
代入f(x+1)=x2+x,
得f(t)=(t-1)2+(t-1)=t2-t,t∈R,
即f(x)=x2-x.
(2)由f(x)是一次函数,设f(x)=ax+b(a≠0),
则f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b=4x-1,
所以
解得或
所以f(x)=2x-或f(x)=-2x+1.
(3)由2f(x)+f=2x, ①
将x换成,则换成x,
得2f+f(x)=, ②
①×2-②,得3f(x)=4x-,
所以f(x)=x-.]
求函数解析式的常用方法
?1?待定系数法:若已知函数的类型,可用待定系数法求解,即由函数类型设出函数解析式,再根据条件列方程?组?,通过解方程?组?求出待定系数,进而求出函数解析式.
?2?换元法?有时可用“配凑法”?:已知函数f[g?x?]的解析式求f?x?的解析式,可用换元法?或“配凑法”?,即令g?x?=t,反解出x,然后代入f[g?x?]中求出f?t?,从而求出f?x?.
?3?消元法?或解方程组法?:在已知式子中,含有关于两个不同变量的函数,而这两个变量有着某种关系,这时就要依据两个变量的关系,建立一个新的关于这两个变量的式子,由两个式子建立方程组,通过解方程组消去一个变量,得到目标变量的解析式,这种方法叫做消元法?或解方程组法?.
2.(1)设函数g(x)=2x-1,则g(x+2)=( )
A.2x+1 B.2x-1
C.2x+3 D.2x-3
(2)设f(x)=2x-3,g(x+2)=f(x),则g(x)=( )
A.2x+1 B.2x+3
C.2x-7 D.2x-3
(1)C (2)C [(1)因为g(x)=2x-1,所以g(x+2)=2(x+2)-1=2x+3.
(2)g(x+2)=f(x)=2x-3,令t=x+2,则x=t-2.
所以g(t)=2(t-2)-3=2t-7,即g(x)=2x-7.]
分段函数及应用
[探究问题]
1.已知函数f(x)=3|x-1|-2.
(1)把函数f(x)写成分段的形式;
(2)画出函数f(x)的图像;
(3)观察f(x)的图像,它是轴对称图形吗?若是,它的对称轴是什么?
(4)如何由函数g(x)=3|x|的图像得到f(x)=3|x-1|-2的图像?
提示:(1)f(x)=
(2)分段画函数图像:
(3)f(x)的图像是轴对称图形,其对称轴为直线x=1.
(4)把函数y=3|x|的图像向右平移1个单位长度,再向下平移2个单位长度可得到函数y=3|x-1|-2的图像.
2.设函数f(x)=
(1)求f与f;
(2)若f(x0)=4,求实数x0的值.
提示:(1)f=-=,f=2=.
(2)由f(x0)=4,
得或
解得x0=-4或2.
3.对于探究2中的函数,探究以下问题.
(1)若f(x)≤,求x的取值范围;
(2)求函数f(x)的值域.
提示:(1)由f(x)≤,
得或
解得-≤x≤0,或0
(2)当x≤0时,f(x)≥0;当x>0时,f(x)>0,
所以,f(x)的值域为[0,+∞)∪(0,+∞)=[0,+∞).
【例3】 已知f(x)=
(1)求f{f[f(5)]}的值;
(2)画出该函数的图像;
(3)根据所画图像,写出函数的定义域,值域.
[思路探究] (1)从里向外依次求值,每一次求值时,应先判断自变量的取值属于哪一段,再利用该段的解析式求值;(2)分段画函数图像;(3)观察函数图像写出定义域,值域.
[解] (1)f{f[f(5)]}=f[f(-3)]=f(1)=-1.
(2)
(3)定义域为(-∞,0]∪(0,4]∪(4,+∞)=R,值域为(-∞,4]∪[-1,8]∪(-∞,-2)=R.
1.分段函数求值,一定要注意所给自变量的值所在的范围,代入相应的解析式求得.
2.多层“f”的问题,要按照“由里到外”的顺序,层层处理.
3.已知分段函数的函数值求相对应的自变量的值,可分段利用函数解析式求得自变量的值,但应注意检验分段解析式的适用范围,也可先判断每一段上的函数值的范围,确定解析式再求解.
4.研究分段函数的性质时,应根据“先分后合”的原则,尤其是在作分段函数的图像时,可先将各段的图像分别画出来,再将它们连在一起得到整个函数的图像.
3.(1)函数f(x)=则f(2)=( )
A.-1 B.0
C.1 D.2
(2)已知f(x)=若f(x)>2,求x的取值范围.
(1)A [f(2)=f(2-1)=f(1)=1-2=-1.]
(2)解:当x≥-2时,f(x)=x+2,
由f(x)>2,得x+2>2,
解得x>0,故x>0;
当x<-2时,f(x)=-x-2,
由f(x)>2,得-x-2>2,
解得x<-4,故x<-4.
综上可得:x>0或x<-4.
1.函数三种表示法的优缺点
2.理解分段函数应注意的问题
(1)分段函数是一个函数,其定义域是各段“定义域”的并集,其值域是各段“值域”的并集.写定义域时,区间的端点需不重不漏.
(2)求分段函数的函数值时,自变量的取值属于哪一段,就用哪一段的解析式.
(3)研究分段函数时,应根据“先分后合”的原则,尤其是作分段函数的图像时,可先将各段的图像分别画出来,从而得到整个函数的图像.
3.求函数解析式常用的方法有:(1)待定系数法;(2)换元法;(3)配凑法;(4)消元法等.
1.思考辨析
(1)任何一个函数都可以用解析法表示.( )
(2)y=是分段函数.( )
(3)函数y=的值域是[0,+∞).( )
[答案] (1)× (2)× (3)√
2.已知f(x2-1)=x4-x2+1,则f(x)=________.
x2+x+1(x≥-1) [因为f(x2-1)=x4-x2+1=(x2-1)2+(x2-1)+1,所以f(x)=x2+x+1(x≥-1).]
3.如图,函数f(x)的图像是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),那么f的值等于________.
2 [由函数f(x)图像,知f(1)=2,f(3)=1,
∴f=f(1)=2.]
4.已知函数y=|x-1|+|x+2|.
(1)作出函数的图像;
(2)写出函数的值域;
(3)判断方程|x-1|+|x+2|=4有多少个实数解?
[解] (1)首先考虑去掉解析式中的绝对值符号,第一个绝对值的分段点x=1,第二个绝对值的分段点x=-2,这样数轴被分为三部分:(-∞,-2],(-2,1],(1,+∞).
所以已知函数可写成分段函数形式:
y=|x-1|+|x+2|=
在相应的x取值范围内,分别作出相应函数的图像,如图所示,即为所求函数的图像.
(2)根据函数的图像可知:值域为[3,+∞).
(3)由于直线y=4与函数y=|x-1|+|x+2|的图像有2个交点,所以,方程|x-1|+|x+2|=4有2个实数解.
