高中数学北师大版必修1学案:第2章函数章末复习课
文档属性
| 名称 | 高中数学北师大版必修1学案:第2章函数章末复习课 |
|
|
| 格式 | zip | ||
| 文件大小 | 461.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-16 23:22:21 | ||
图片预览



文档简介
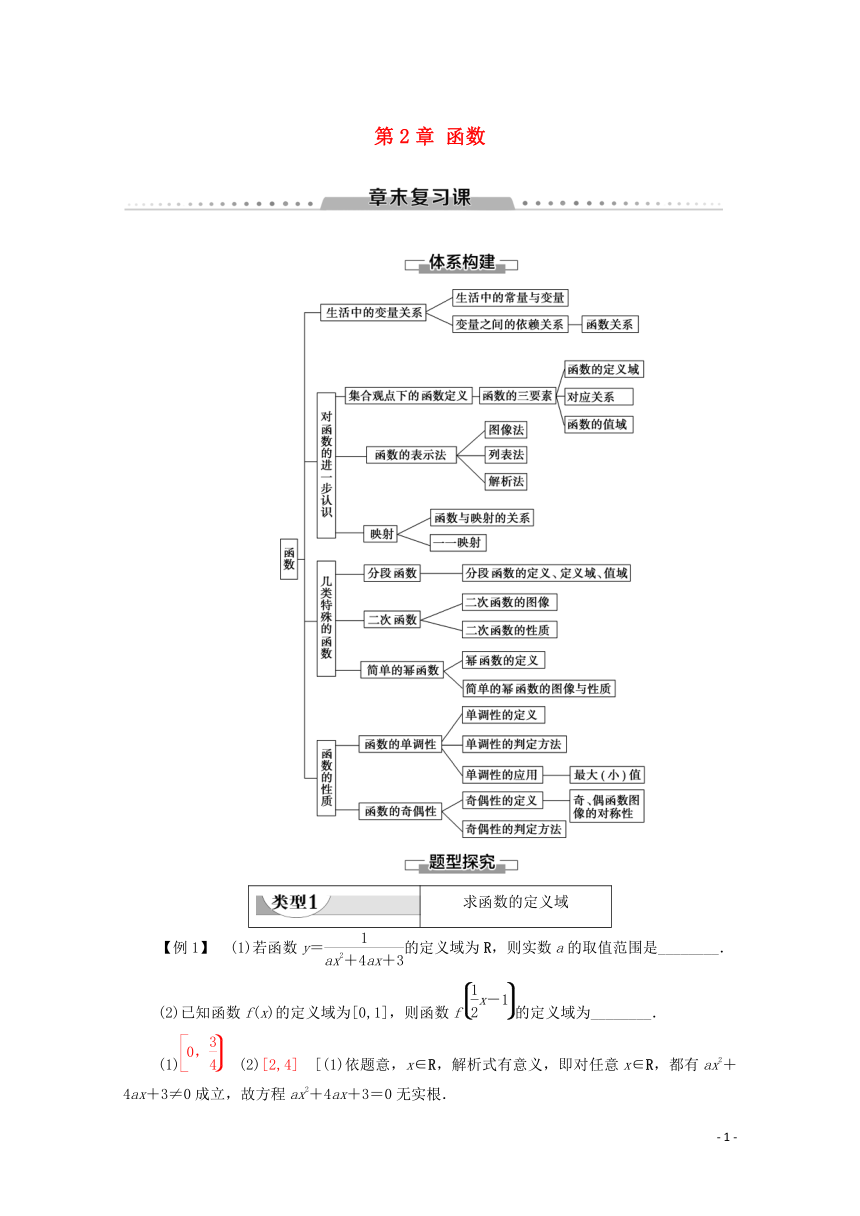
第2章 函数
求函数的定义域
【例1】 (1)若函数y=的定义域为R,则实数a的取值范围是________.
(2)已知函数f(x)的定义域为[0,1],则函数f的定义域为________.
(1) (2)[2,4] [(1)依题意,x∈R,解析式有意义,即对任意x∈R,都有ax2+4ax+3≠0成立,故方程ax2+4ax+3=0无实根.
①当a=0时,3≠0满足要求;
②当a≠0时,则有Δ=16a2-12a<0,即0<a<时满足要求.综上可知a∈.
(2)由题意知,0≤x-1≤1,
解得2≤x≤4.
因此,函数f的定义域为[2,4].]
求函数定义域的类型与方法
?1?已给出函数解析式:函数的定义域是使解析式有意义的自变量的取值范围.
?2?实际问题:求函数的定义域既要考虑解析式有意义,还应考虑使实际问题有意义.
?3?复合函数问题:
①若f?x?的定义域为[a,b],f?g?x??的定义域应由a≤g?x?≤b解出;
②若f?g?x??的定义域为[a,b],则f?x?的定义域为g?x?在[a,b]上的值域.,注意:①f?x?中的x与f?g?x??中的g?x?地位相同;②定义域所指永远是x的范围.
1.已知函数f(2x-1)的定义域为[0,1),求f(1-3x)的定义域.
[解] 由0≤x<1,得-1≤2x-1<1,
所以,f(x)的定义域是[-1,1).
由-1≤1-3x<1,得0所以,函数f(1-3x)的定义域是.
函数的单调性
【例2】 (1)已知函数f(x)在R上单调递减,且f(2)=0,若f(x-1)>0,则x的取值范围是________.
(2)函数y=|2x-1|的单调递增区间是________.
[思路探究] (1)将原不等式化为f(x-1)>f(2),再利用函数的单调性将其转化为x-1<2来解;(2)画出函数的图像求解.
(1)x<3 (2) [(1)∵f(2)=0,∴不等式f(x-1)>0,即为f(x-1)>f(2),
又f(x)是R上的减函数,
则x-1<2,解得x<3.
(2)函数y=|2x-1|的图像如下:
由图像知,其单调递增区间是.]
?1?f?x?是A上的增函数?对任意x1,x2∈A,当x1≠x2时,f(f?x2?-f?x1?,x2-x1)>0,f?x?是A上的减函数?对任意x1,x2∈A,当x1≠x2时,.
?2?若f?x?是单调递增?减?函数,则
①f?x2?>f?x1??x2>x1?x2②f?x2?=f?x1??x2=x1;
③f?x2?x1?.
2.(1)已知f(x)=x,若0A.f(a)B.fC.f(a)D.f(2)已知函数y=在(1,2)上单调递增,则实数a的取值范围是( )
A.(0,1] B.[1,2]
C.[1,+∞) D.[2,+∞)
(1)C (2)C [(1)由0又f(x)=x是增函数,
则f(a)(2)依题意,
解得a≥1.]
函数的奇偶性
[探究问题]
1.具有奇偶性的函数其定义域有何特点?
提示:具有奇偶性的函数,其定义域关于原点对称,由奇函数的定义可知f(-x)=-f(x),故变量x,-x均在定义域中,同理,对于偶函数,由f(-x)=f(x)可知,-x,x也均在定义域内.
2.既是奇函数,又是偶函数的函数不存在,对吗?
提示:不对.如函数y=0(x∈R),其图像既关于原点对称,又关于y轴对称,所以函数y=0(x∈R)既是奇函数又是偶函数.
3.定义在R上的奇函数f(x),f(0)的值是多少?
提示:f(0)=0.
【例3】 (1)已知函数g(x)=f(x)+x是偶函数,且f(2)=1,则f(-2)=( )
A.2 B.3
C.4 D.5
(2)若函数y=的最大值为M,最小值为m,则M+m=________.
[思路探究] (1)利用g(-2)=g(2)求解;(2)变形得y=1+,先判断y=是奇函数,再利用奇函数的最大值与最小值之和为零求解.
(1)D (2)2 [(1)由g(x)=f(x)+x是偶函数,
得g(-2)=g(2),即f(-2)+(-2)=f(2)+2,
所以,f(-2)=f(2)+4=1+4=5.
(2)y==1+,
令f(x)=,则f(x)是奇函数.
∴f(x)max+f(x)min=0,
∴M+m=[1+f(x)max]+[1+f(x)min]=2+[f(x)max+f(x)min]=2.]
函数奇偶性的几个结论
?1?如果一个奇函数f?x?在原点处有定义,那么f?0?=0.
?2?如果函数f?x?是偶函数,那么f?|x|?=f?x?.
?3?奇函数在关于原点对称的区间上单调性相同;偶函数在关于原点对称的区间上单调性相反.
3.(1)定义在R上的偶函数f(x)在[0,+∞)上是增函数,若f(a)A.ab
C.|a|<|b| D.0≤ab≥0
(2)已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x2+1,则f(1)+g(1)等于( )
A.-3 B.-1
C.1 D.3
(1)C (2)C [(1)由f(x)是偶函数,得f(|a|)=f(a),f(|b|)=f(b).
又f(a)又f(x)在[0,+∞)上是增函数.
则|a|<|b|.故选C.
(2)f(-1)-g(-1)=(-1)3+(-1)2+1=1,
又f(-1)=f(1),g(-1)=-g(1),
则f(1)+g(1)=1.]
函数的最大(小)值
已知函数f(x)=ax2+(2a-1)x-3在区间上的最大值为1,求实数a的值.
[解] 当a=0时,f(x)=-x-3,f(x)在上不能取得1,故a≠0.
f(x)=ax2+(2a-1)x-3(a≠0)的对称轴方程为x0=.
(1)令f=1,解得a=-,
此时x0=-∈,
因为a<0,f(x0)最大,所以f=1不合适.
(2)令f(2)=1,解得a=,
此时x0=-∈.
因为a>0,x0=-∈,且距右端点2较远,
所以f(2)最大,合适.
(3)令f(x0)=1,得a=(-3±2),
验证后知只有a=(-3-2)才合适.
综上所述,a=或a=-(3+2).
应用分类讨论思想解决问题的关键是确定分类的标准,从而使分类不重不漏.其步骤:
?1?确定分类讨论的对象,即对哪个参数进行讨论;?2?对所讨论的对象进行合理的分类;?3?逐个讨论;?4?归纳总结,即对各类情况进行归纳,得出结论.
4.(1)对于任意x∈R,函数f(x)表示-x+3,x+,x2-4x+3中的较大者,则f(x)的最小值是________.
(2)已知函数f(x)=,对于其定义域的任意x,都有f(-1)≤f(x)≤f(1),则b=________,c=________.
(1)2 (2)2 3 [(1)如图,分别画出三个函数的图像,得到三个交点A(0,3),B(1,2),C(5,8).
从图像观察可得函数f(x)的表达式:
f(x)=
f(x)的图像是图中的实线部分,图像的最低点是点B(1,2),所以f(x)的最小值是2.
(2)依题意,f(-1)是f(x)的最小值,f(1)是函数的最大值,
所以,f(-1)=0,直线x=1是抛物线y=-x2+bx+c的对称轴.
所以,f(3)=0.
所以,
解得,]
求函数的定义域
【例1】 (1)若函数y=的定义域为R,则实数a的取值范围是________.
(2)已知函数f(x)的定义域为[0,1],则函数f的定义域为________.
(1) (2)[2,4] [(1)依题意,x∈R,解析式有意义,即对任意x∈R,都有ax2+4ax+3≠0成立,故方程ax2+4ax+3=0无实根.
①当a=0时,3≠0满足要求;
②当a≠0时,则有Δ=16a2-12a<0,即0<a<时满足要求.综上可知a∈.
(2)由题意知,0≤x-1≤1,
解得2≤x≤4.
因此,函数f的定义域为[2,4].]
求函数定义域的类型与方法
?1?已给出函数解析式:函数的定义域是使解析式有意义的自变量的取值范围.
?2?实际问题:求函数的定义域既要考虑解析式有意义,还应考虑使实际问题有意义.
?3?复合函数问题:
①若f?x?的定义域为[a,b],f?g?x??的定义域应由a≤g?x?≤b解出;
②若f?g?x??的定义域为[a,b],则f?x?的定义域为g?x?在[a,b]上的值域.,注意:①f?x?中的x与f?g?x??中的g?x?地位相同;②定义域所指永远是x的范围.
1.已知函数f(2x-1)的定义域为[0,1),求f(1-3x)的定义域.
[解] 由0≤x<1,得-1≤2x-1<1,
所以,f(x)的定义域是[-1,1).
由-1≤1-3x<1,得0
函数的单调性
【例2】 (1)已知函数f(x)在R上单调递减,且f(2)=0,若f(x-1)>0,则x的取值范围是________.
(2)函数y=|2x-1|的单调递增区间是________.
[思路探究] (1)将原不等式化为f(x-1)>f(2),再利用函数的单调性将其转化为x-1<2来解;(2)画出函数的图像求解.
(1)x<3 (2) [(1)∵f(2)=0,∴不等式f(x-1)>0,即为f(x-1)>f(2),
又f(x)是R上的减函数,
则x-1<2,解得x<3.
(2)函数y=|2x-1|的图像如下:
由图像知,其单调递增区间是.]
?1?f?x?是A上的增函数?对任意x1,x2∈A,当x1≠x2时,f(f?x2?-f?x1?,x2-x1)>0,f?x?是A上的减函数?对任意x1,x2∈A,当x1≠x2时,.
?2?若f?x?是单调递增?减?函数,则
①f?x2?>f?x1??x2>x1?x2
③f?x2?
2.(1)已知f(x)=x,若0
A.(0,1] B.[1,2]
C.[1,+∞) D.[2,+∞)
(1)C (2)C [(1)由0
则f(a)
解得a≥1.]
函数的奇偶性
[探究问题]
1.具有奇偶性的函数其定义域有何特点?
提示:具有奇偶性的函数,其定义域关于原点对称,由奇函数的定义可知f(-x)=-f(x),故变量x,-x均在定义域中,同理,对于偶函数,由f(-x)=f(x)可知,-x,x也均在定义域内.
2.既是奇函数,又是偶函数的函数不存在,对吗?
提示:不对.如函数y=0(x∈R),其图像既关于原点对称,又关于y轴对称,所以函数y=0(x∈R)既是奇函数又是偶函数.
3.定义在R上的奇函数f(x),f(0)的值是多少?
提示:f(0)=0.
【例3】 (1)已知函数g(x)=f(x)+x是偶函数,且f(2)=1,则f(-2)=( )
A.2 B.3
C.4 D.5
(2)若函数y=的最大值为M,最小值为m,则M+m=________.
[思路探究] (1)利用g(-2)=g(2)求解;(2)变形得y=1+,先判断y=是奇函数,再利用奇函数的最大值与最小值之和为零求解.
(1)D (2)2 [(1)由g(x)=f(x)+x是偶函数,
得g(-2)=g(2),即f(-2)+(-2)=f(2)+2,
所以,f(-2)=f(2)+4=1+4=5.
(2)y==1+,
令f(x)=,则f(x)是奇函数.
∴f(x)max+f(x)min=0,
∴M+m=[1+f(x)max]+[1+f(x)min]=2+[f(x)max+f(x)min]=2.]
函数奇偶性的几个结论
?1?如果一个奇函数f?x?在原点处有定义,那么f?0?=0.
?2?如果函数f?x?是偶函数,那么f?|x|?=f?x?.
?3?奇函数在关于原点对称的区间上单调性相同;偶函数在关于原点对称的区间上单调性相反.
3.(1)定义在R上的偶函数f(x)在[0,+∞)上是增函数,若f(a)
C.|a|<|b| D.0≤a
(2)已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x2+1,则f(1)+g(1)等于( )
A.-3 B.-1
C.1 D.3
(1)C (2)C [(1)由f(x)是偶函数,得f(|a|)=f(a),f(|b|)=f(b).
又f(a)
则|a|<|b|.故选C.
(2)f(-1)-g(-1)=(-1)3+(-1)2+1=1,
又f(-1)=f(1),g(-1)=-g(1),
则f(1)+g(1)=1.]
函数的最大(小)值
已知函数f(x)=ax2+(2a-1)x-3在区间上的最大值为1,求实数a的值.
[解] 当a=0时,f(x)=-x-3,f(x)在上不能取得1,故a≠0.
f(x)=ax2+(2a-1)x-3(a≠0)的对称轴方程为x0=.
(1)令f=1,解得a=-,
此时x0=-∈,
因为a<0,f(x0)最大,所以f=1不合适.
(2)令f(2)=1,解得a=,
此时x0=-∈.
因为a>0,x0=-∈,且距右端点2较远,
所以f(2)最大,合适.
(3)令f(x0)=1,得a=(-3±2),
验证后知只有a=(-3-2)才合适.
综上所述,a=或a=-(3+2).
应用分类讨论思想解决问题的关键是确定分类的标准,从而使分类不重不漏.其步骤:
?1?确定分类讨论的对象,即对哪个参数进行讨论;?2?对所讨论的对象进行合理的分类;?3?逐个讨论;?4?归纳总结,即对各类情况进行归纳,得出结论.
4.(1)对于任意x∈R,函数f(x)表示-x+3,x+,x2-4x+3中的较大者,则f(x)的最小值是________.
(2)已知函数f(x)=,对于其定义域的任意x,都有f(-1)≤f(x)≤f(1),则b=________,c=________.
(1)2 (2)2 3 [(1)如图,分别画出三个函数的图像,得到三个交点A(0,3),B(1,2),C(5,8).
从图像观察可得函数f(x)的表达式:
f(x)=
f(x)的图像是图中的实线部分,图像的最低点是点B(1,2),所以f(x)的最小值是2.
(2)依题意,f(-1)是f(x)的最小值,f(1)是函数的最大值,
所以,f(-1)=0,直线x=1是抛物线y=-x2+bx+c的对称轴.
所以,f(3)=0.
所以,
解得,]
