高中数学北师大版必修1学案:第3章指数函数和对数函数章末复习课
文档属性
| 名称 | 高中数学北师大版必修1学案:第3章指数函数和对数函数章末复习课 |
|
|
| 格式 | zip | ||
| 文件大小 | 414.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-16 00:00:00 | ||
图片预览


文档简介
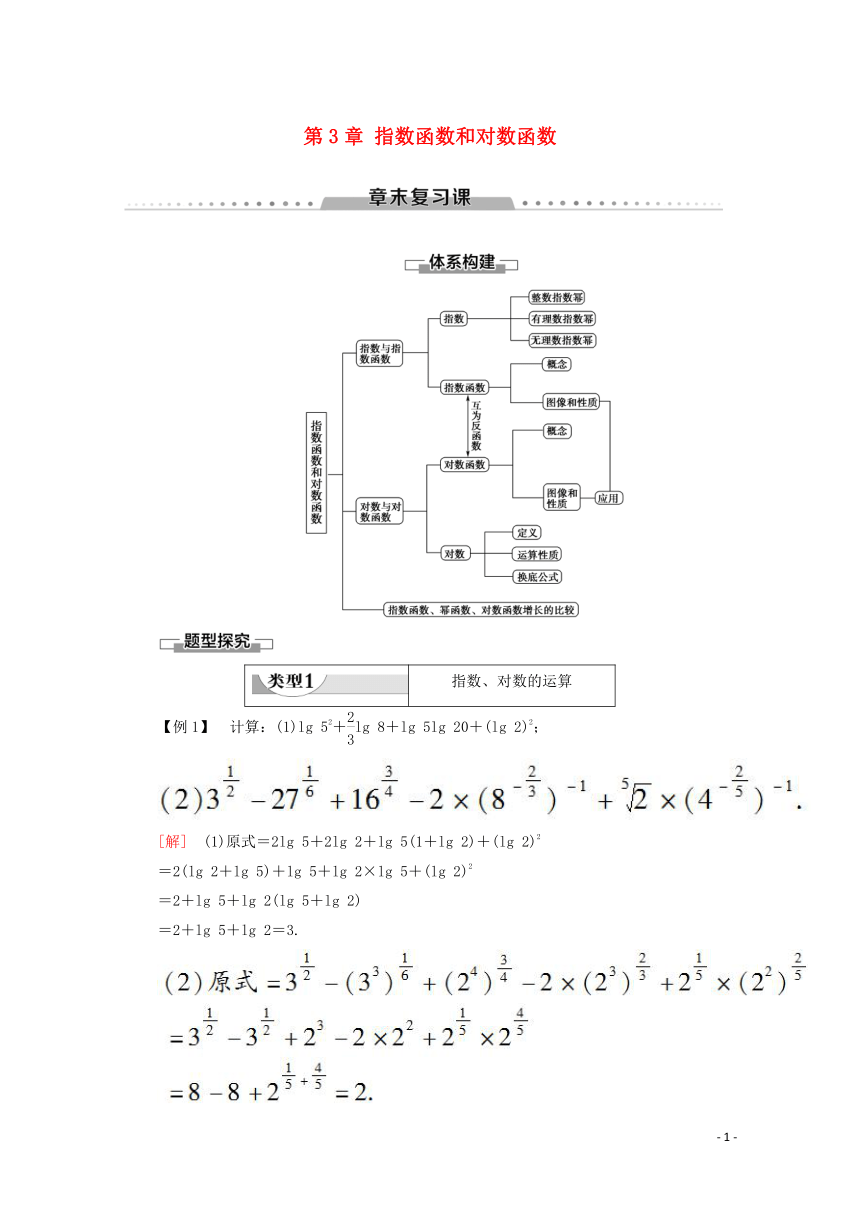
第3章 指数函数和对数函数
指数、对数的运算
【例1】 计算:(1)lg 52+lg 8+lg 5lg 20+(lg 2)2;
[解] (1)原式=2lg 5+2lg 2+lg 5(1+lg 2)+(lg 2)2
=2(lg 2+lg 5)+lg 5+lg 2×lg 5+(lg 2)2
=2+lg 5+lg 2(lg 5+lg 2)
=2+lg 5+lg 2=3.
1.指数幂运算的一般原则
(1)有括号的先算括号里的,无括号的先做指数运算.
(2)先乘除后加减,负指数幂化成正指数幂的倒数.
(3)底数是负数,先确定符号,底数是小数,先化成分数,底数是带分数的,先化成假分数.
(4)若是根式,应化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运算性质来解答.
2.对数运算的常用方法
(1)首先利用幂的运算把底数或真数进行变形,化成分数指数幂的形式,使幂的底数最简,然后正用对数运算性质化简合并.
(2)将对数式化为同底数对数的和、差、倍数运算,然后逆用对数的运算性质,转化为同底对数真数的积、商、幂的运算.
1.已知a>b>1,若logab+logba=,ab=ba,则a=________,b=________.
4,2 [由logab+logba=,得logab+=,
∴(logab)2-logab+1=0,
解得logab=或2,又a>b>1,则logab=,
由ab=ba,得b=alogab,
∴b=a,
∴logaa=,即loga+1=,
∴loga=-,
∴a-=,
∴a=4,b=2.]
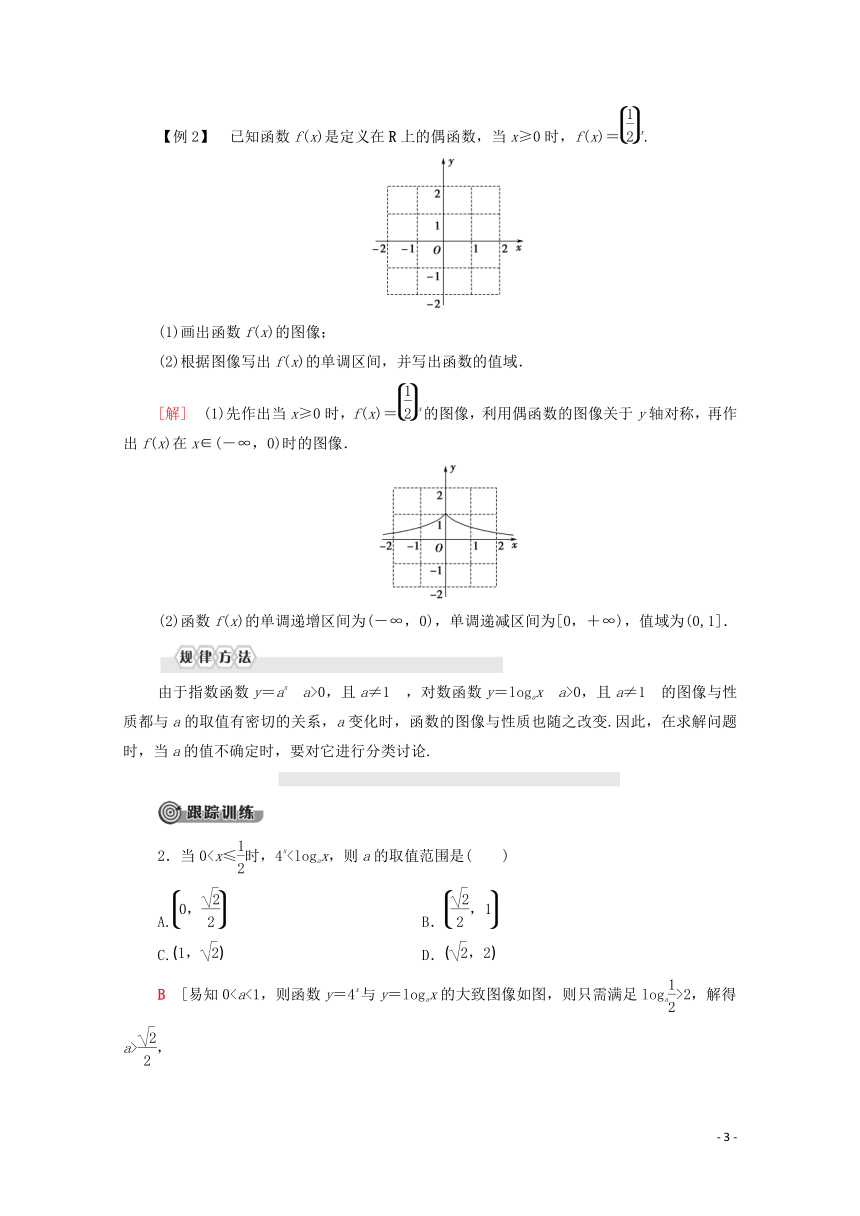
指(对)数函数的图像及应用
【例2】 已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x.
(1)画出函数f(x)的图像;
(2)根据图像写出f(x)的单调区间,并写出函数的值域.
[解] (1)先作出当x≥0时,f(x)=x的图像,利用偶函数的图像关于y轴对称,再作出f(x)在x∈(-∞,0)时的图像.
(2)函数f(x)的单调递增区间为(-∞,0),单调递减区间为[0,+∞),值域为(0,1].
由于指数函数y=ax?a>0,且a≠1?,对数函数y=logax?a>0,且a≠1?的图像与性质都与a的取值有密切的关系,a变化时,函数的图像与性质也随之改变.因此,在求解问题时,当a的值不确定时,要对它进行分类讨论.
2.当0A. B.
C. D.
B [易知02,解得a>,
∴]
比较大小
【例3】 (1)三个数a=0.67,b=70.6,c=log0.76的大小关系为( )
A.bC.c( )
A.bC.b(1)C (2)A [(1)结合y=0.6x,y=7x和y=log0.7x的图象,可知01,c<0,故c比较两数?式?或几个数?式?大小问题是一个重要题型,它主要是考查幂函数、指数函数、对数函数图像与性质的应用及差值比较法与商值比较法的应用,常用的方法有单调性法、图像法、中间量搭桥法、作差法、作商法、分析转化法等.
3.若a>b>1,0A.acC.alogbcC [对于选项A,考虑幂函数y=xc,因为c>0,所以y=xc为增函数,又a>b>1,所以ac>bc,A错.对于选项B,abc指(对)数函数的性质及应用
[探究问题]
1.已知f(x)=loga|x|,满足f(-5)=1,试画出函数f(x)的图像.
提示:因为f(-5)=1,所以loga5=1,即a=5,
故f(x)=log5|x|=
所以函数y=log5|x|的图像如图所示.
2.试写出函数f(x)=log5|x|的值域及单调区间.
提示:由探究1的图像知f(x)的值域为R,递增区间为(0,+∞),递减区间为(-∞,0).
3.把探究1中的函数改为y=logb(x-1)(b>0且b≠1),试求该函数恒过的定点.
提示:令x-1=1得x=2,又y=logb1=0,故该函数恒过定点(2,0).
已知函数f(x)=loga(a>0,且a≠1)是奇函数.
(1)求实数m的值;
(2)探究函数f(x)在(1,+∞)上的单调性.
[思路探究] (1)利用奇函数的定义求解;(2)利用复合函数单调性的判断方法判断.
[解] (1)由f(x)是奇函数,得f(-x)=-f(x),
即loga=-loga
∴loga+loga=0,
loga=0,
∴=1,
∴(1-m2)x2=0,
∴1-m2=0,解得m±1.
又当m=1时,==-1,故m=1不合题意.
所以m=-1.
(2)由(1)知,f(x)=loga=loga.
函数u=1+在区间(1,+∞)上单调递减.
∴当a>1时,f(x)在区间(1,+∞)上单调递减;
当0求解与指?对?数函数有关的复合函数的问题时,需要弄清楚三个方面的问题:
?1?定义域,所有问题都必须在定义域内讨论;
?2?底数与1的大小关系;
?3?复合函数的构成,如y=af?x?是由y=au与u=f?x?构成的.
4.已知f(x)=lg .
(1)若f(x)的定义域为(-∞,1),求a的值;
(2)若f(x)在x∈(-∞,1)内恒有意义,求a的取值范围.
[解] (1)由函数f(x)的定义域为(-∞,1),得关于x的不等式1+2x+a·3x>0的解集为(-∞,1),即a>-=g(x)的解集为(-∞,1).
∵g(x)在R上是增函数,
∴不等式g(1)>g(x)的解集为(-∞,1),
∴a=g(1)=-1.
(2)由已知得,不等式1+2x+a·3x>0对x∈(-∞,1)恒成立,
即a>-=g(x)对x∈(-∞,1)恒成立;
故a>g(x)max,∵g(x)在区间(-∞,1)上是增函数,
∴g(x)
指数、对数的运算
【例1】 计算:(1)lg 52+lg 8+lg 5lg 20+(lg 2)2;
[解] (1)原式=2lg 5+2lg 2+lg 5(1+lg 2)+(lg 2)2
=2(lg 2+lg 5)+lg 5+lg 2×lg 5+(lg 2)2
=2+lg 5+lg 2(lg 5+lg 2)
=2+lg 5+lg 2=3.
1.指数幂运算的一般原则
(1)有括号的先算括号里的,无括号的先做指数运算.
(2)先乘除后加减,负指数幂化成正指数幂的倒数.
(3)底数是负数,先确定符号,底数是小数,先化成分数,底数是带分数的,先化成假分数.
(4)若是根式,应化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运算性质来解答.
2.对数运算的常用方法
(1)首先利用幂的运算把底数或真数进行变形,化成分数指数幂的形式,使幂的底数最简,然后正用对数运算性质化简合并.
(2)将对数式化为同底数对数的和、差、倍数运算,然后逆用对数的运算性质,转化为同底对数真数的积、商、幂的运算.
1.已知a>b>1,若logab+logba=,ab=ba,则a=________,b=________.
4,2 [由logab+logba=,得logab+=,
∴(logab)2-logab+1=0,
解得logab=或2,又a>b>1,则logab=,
由ab=ba,得b=alogab,
∴b=a,
∴logaa=,即loga+1=,
∴loga=-,
∴a-=,
∴a=4,b=2.]
指(对)数函数的图像及应用
【例2】 已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x.
(1)画出函数f(x)的图像;
(2)根据图像写出f(x)的单调区间,并写出函数的值域.
[解] (1)先作出当x≥0时,f(x)=x的图像,利用偶函数的图像关于y轴对称,再作出f(x)在x∈(-∞,0)时的图像.
(2)函数f(x)的单调递增区间为(-∞,0),单调递减区间为[0,+∞),值域为(0,1].
由于指数函数y=ax?a>0,且a≠1?,对数函数y=logax?a>0,且a≠1?的图像与性质都与a的取值有密切的关系,a变化时,函数的图像与性质也随之改变.因此,在求解问题时,当a的值不确定时,要对它进行分类讨论.
2.当0
C. D.
B [易知0
∴
比较大小
【例3】 (1)三个数a=0.67,b=70.6,c=log0.76的大小关系为( )
A.b
A.b
3.若a>b>1,0
[探究问题]
1.已知f(x)=loga|x|,满足f(-5)=1,试画出函数f(x)的图像.
提示:因为f(-5)=1,所以loga5=1,即a=5,
故f(x)=log5|x|=
所以函数y=log5|x|的图像如图所示.
2.试写出函数f(x)=log5|x|的值域及单调区间.
提示:由探究1的图像知f(x)的值域为R,递增区间为(0,+∞),递减区间为(-∞,0).
3.把探究1中的函数改为y=logb(x-1)(b>0且b≠1),试求该函数恒过的定点.
提示:令x-1=1得x=2,又y=logb1=0,故该函数恒过定点(2,0).
已知函数f(x)=loga(a>0,且a≠1)是奇函数.
(1)求实数m的值;
(2)探究函数f(x)在(1,+∞)上的单调性.
[思路探究] (1)利用奇函数的定义求解;(2)利用复合函数单调性的判断方法判断.
[解] (1)由f(x)是奇函数,得f(-x)=-f(x),
即loga=-loga
∴loga+loga=0,
loga=0,
∴=1,
∴(1-m2)x2=0,
∴1-m2=0,解得m±1.
又当m=1时,==-1,故m=1不合题意.
所以m=-1.
(2)由(1)知,f(x)=loga=loga.
函数u=1+在区间(1,+∞)上单调递减.
∴当a>1时,f(x)在区间(1,+∞)上单调递减;
当0
?1?定义域,所有问题都必须在定义域内讨论;
?2?底数与1的大小关系;
?3?复合函数的构成,如y=af?x?是由y=au与u=f?x?构成的.
4.已知f(x)=lg .
(1)若f(x)的定义域为(-∞,1),求a的值;
(2)若f(x)在x∈(-∞,1)内恒有意义,求a的取值范围.
[解] (1)由函数f(x)的定义域为(-∞,1),得关于x的不等式1+2x+a·3x>0的解集为(-∞,1),即a>-=g(x)的解集为(-∞,1).
∵g(x)在R上是增函数,
∴不等式g(1)>g(x)的解集为(-∞,1),
∴a=g(1)=-1.
(2)由已知得,不等式1+2x+a·3x>0对x∈(-∞,1)恒成立,
即a>-=g(x)对x∈(-∞,1)恒成立;
故a>g(x)max,∵g(x)在区间(-∞,1)上是增函数,
∴g(x)
