湘教版九年级数学上册 第2章 一元二次方程2.1 一元二次方程教学课件(共28张)
文档属性
| 名称 | 湘教版九年级数学上册 第2章 一元二次方程2.1 一元二次方程教学课件(共28张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-17 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
一元二次方程
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
今天,是小芳的生日,她的四个小伙伴约好为她举办一个生日party,张叔叔刚好路过,想知道小芳的年龄却又不好意思当面询问,便展开了一场数学大讨论。
我是最小的,我们5个的年龄从小到大依次恰好相差1岁。
我们中较大的两个的年龄和的平方恰好等于较小的三个人的年龄和的平方。
同学们能猜出小芳的年龄了吗?
小芳
新课导入
想一想
解:如果我们假设小芳的年龄为x,根据题意,得:
对于这类方程,同学们之前有见过吗?它与之前我们所学过的方程有什么不同呢?接下来就让我们一起来探究本节课的内容吧!
02 新知探究
新知探究
1.一元二次方程的概念
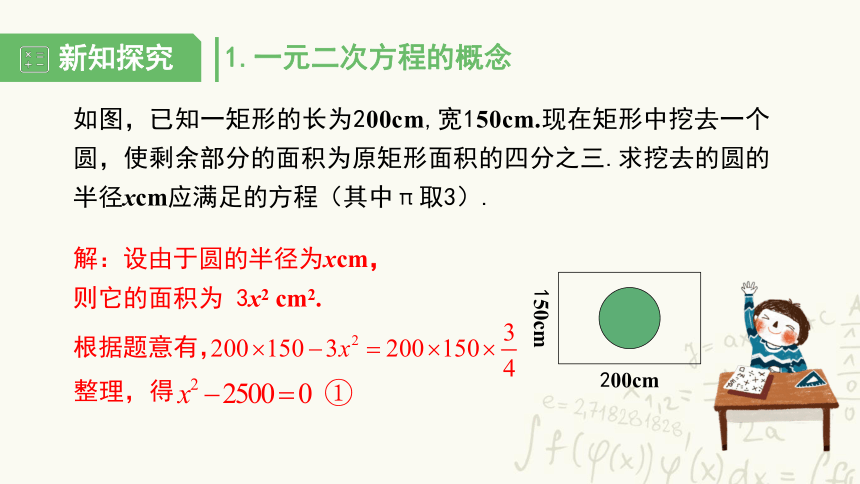
如图,已知一矩形的长为200cm,宽150cm.现在矩形中挖去一个圆,使剩余部分的面积为原矩形面积的四分之三.求挖去的圆的半径xcm应满足的方程(其中π取3).
150cm
200cm
解:设由于圆的半径为xcm,则它的面积为 3x2 cm2.
根据题意有,
整理,得
新知探究
1.一元二次方程的概念
如图,据某市交通部门统计,前年该市汽车拥有量为75万辆,两年后增加到108万辆.求该市两年来汽车拥有量的年平均增长率x应满足的方程.
解:该市两年来汽车拥有量的年平均增长率为x,根据题意有:
整理,得
新知探究
1.一元二次方程的概念
方程①、②都不是一元一次方程.那么这两个方程与一元一次方程的区别在哪里?它们有什么共同特点呢?
特点:
①都是整式方程;
②只含一个未知数;
③未知数的最高次数是2.
新知探究
只含有一个未知数x的整式方程,并且都可以整理为ax2+bx+c=0(a,b,c为常数, a≠0)的形式,这样的方程叫做一元二次方程.
一元二次方程的一般形式是
ax2+bx +c = 0(a , b , c为常数, a≠0)
其中a 称为二次项系数,b 称为一次项系数,c 称为常数项.
1.一元二次方程的概念
例如 中,二次项系数是1,一次项系数是0,常数项为-2500.
新知探究
为什么一般形式中ax2+bx+c=0要限制a≠0,b、c 可以为零吗?
当 a = 0 时
bx+c = 0
当 a ≠ 0 , b = 0时 ,
ax2+c = 0
当 a ≠ 0 , c = 0时 ,
ax2+bx = 0
当 a ≠ 0 ,b = c =0时 ,
ax2 = 0
总结:只要满足a ≠ 0 ,b , c 可以为任意实数.
1.一元二次方程的概念
新知探究
下列选项中,关于x的一元二次方程的是( )
C
提示
判断一个方程是不是一元二次方程,首先看是不是整式方程;如是再对它进行整理,若能整理为ax2+bx +c = 0(a , b , c为常数, a≠0)
的形式,这个方程就是一元二次方程.
不是整式方程
含两个未知数
化简整理 x2-3x+2=0
少了限制条件 a≠0
1.一元二次方程的概念
新知探究
想一想
一元一次方程与一元二次方程有什么区别与联系?
一元一次方程 一元二次方程
一般式
相同点
不同点
ax=b (a≠0)
ax2+bx+c=0 (a≠0)
整式方程,只含有一个未知数
未知数最高次数是1
未知数最高次数是2
新知探究
了解了一元二次方程的概念和一般形式,你会把一元二次方程化为一般形式吗?
下列方程是一元二次方程吗?若是,指出其中的二次项系数、一次项系数和常数项.
(1)3x (1 – x ) + 10 = 2( x + 2)
(2)5x ( x + 1) + 7 = 5x2 - 4.
解:(1)去括号, 得
3x - 3x2 + 10 = 2x + 4.
移项, 合并同类项, 得
- 3x2 + x + 6 = 0,
这是一元二次方程, 其中二次项系数是-3, 一次项系数是1, 常数项是6.
2.一元二次方程的一般形式
新知探究
(2) 5x ( x + 1) + 7 = 5x2 - 4.
去括号, 得
5x2 + 5x + 7 = 5x2 - 4.
移项, 合并同类项, 得
5x + 11 = 0,
可以看出这个方程没有二次项,因此这是一元一次方程, 不是一元二次方程.
2.一元二次方程的一般形式
新知探究
(1)在确定一元二次方程各项系数时,首先把一元二次方程转化成一般形式,如果在一般形式中二次项系数为负数,那么最好在方程左右两边同乘-1,使二次项系数变为正数;
(2)指出一元二次方程的各项系数时,一定要带上前面的符号;
(3)一元二次方程转化为一般形式后,若没有出现一次项,则=0;若没有出现常数项,则=0.
2.一元二次方程的一般形式
新知探究
如图,一块长方形地,长为200米,建筑商将它分为 A、B、C三个区域,A,B为正方形。现计划A区域建筑住宅区,B区域建筑商场,C区域开辟为公园。若已知C区域的面积为3200,设C区域的长为米,列出关于x的方程?
3.列一元二次方程
A
B
C
200米
x
解:由题意知A,B为正方形,
所以C区域的宽为200-x-x=200-2x
所以(200?2????)×????=3200
去括号移项整理得
03 典型例题
典型例题
1. 下列哪些是一元二次方程?
3x+2=5x-2
x2=0
(x+3)(2x-4)=x2
3y2=(3y+1)(y-2)
x2=x3+x2-1
3x2=5x-1
×
√
√
×
×
√
典型例题
2.一元二次方程 化为一般形式为:_________,二次项系数为___,一次项系数为___,常数项为_____.
=0
其中二次项系数是 1, 一次项系数是 -8, 常数项是 -4.
解析:
3.两个正方形,小正方形的边长比大正方形的边长的一半多4cm,大正方形的面积比小正方形的面积的2倍少32平方厘米,设大正方形边长为x,列出关于x的方程?
典型例题
解:根据题意,小正方形的边长为
大正方形的面积为
去括号移项整理得
04 拓展提高
拓展提高
百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元,为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存,经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件。
要想平均每天销售这种童装1200元,那么每件童装应降价多少元?
思路:审题→列方程→解未知数
解:设每件童装降价x元,那么根据题意每件盈利40-(元),可卖出20+2件
因此有方程式
解得
因为要尽量减少库存,所以取
答:每件童装应降价20元。
05 课堂小结
课堂小结
一元二次方程
概念
是整式方程;
含一个未知数;
最高次数是2.
一般形式
ax2+bx+c=0 (a ≠0)
其中(a≠0)是一元二次方程的必要条件;
列方程解应用问题
准确审题→列方程→解未知数
06 作业布置
完成课本习题2.1 A、B组
作业布置
谢 谢 观 看
一元二次方程
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
今天,是小芳的生日,她的四个小伙伴约好为她举办一个生日party,张叔叔刚好路过,想知道小芳的年龄却又不好意思当面询问,便展开了一场数学大讨论。
我是最小的,我们5个的年龄从小到大依次恰好相差1岁。
我们中较大的两个的年龄和的平方恰好等于较小的三个人的年龄和的平方。
同学们能猜出小芳的年龄了吗?
小芳
新课导入
想一想
解:如果我们假设小芳的年龄为x,根据题意,得:
对于这类方程,同学们之前有见过吗?它与之前我们所学过的方程有什么不同呢?接下来就让我们一起来探究本节课的内容吧!
02 新知探究
新知探究
1.一元二次方程的概念
如图,已知一矩形的长为200cm,宽150cm.现在矩形中挖去一个圆,使剩余部分的面积为原矩形面积的四分之三.求挖去的圆的半径xcm应满足的方程(其中π取3).
150cm
200cm
解:设由于圆的半径为xcm,则它的面积为 3x2 cm2.
根据题意有,
整理,得
新知探究
1.一元二次方程的概念
如图,据某市交通部门统计,前年该市汽车拥有量为75万辆,两年后增加到108万辆.求该市两年来汽车拥有量的年平均增长率x应满足的方程.
解:该市两年来汽车拥有量的年平均增长率为x,根据题意有:
整理,得
新知探究
1.一元二次方程的概念
方程①、②都不是一元一次方程.那么这两个方程与一元一次方程的区别在哪里?它们有什么共同特点呢?
特点:
①都是整式方程;
②只含一个未知数;
③未知数的最高次数是2.
新知探究
只含有一个未知数x的整式方程,并且都可以整理为ax2+bx+c=0(a,b,c为常数, a≠0)的形式,这样的方程叫做一元二次方程.
一元二次方程的一般形式是
ax2+bx +c = 0(a , b , c为常数, a≠0)
其中a 称为二次项系数,b 称为一次项系数,c 称为常数项.
1.一元二次方程的概念
例如 中,二次项系数是1,一次项系数是0,常数项为-2500.
新知探究
为什么一般形式中ax2+bx+c=0要限制a≠0,b、c 可以为零吗?
当 a = 0 时
bx+c = 0
当 a ≠ 0 , b = 0时 ,
ax2+c = 0
当 a ≠ 0 , c = 0时 ,
ax2+bx = 0
当 a ≠ 0 ,b = c =0时 ,
ax2 = 0
总结:只要满足a ≠ 0 ,b , c 可以为任意实数.
1.一元二次方程的概念
新知探究
下列选项中,关于x的一元二次方程的是( )
C
提示
判断一个方程是不是一元二次方程,首先看是不是整式方程;如是再对它进行整理,若能整理为ax2+bx +c = 0(a , b , c为常数, a≠0)
的形式,这个方程就是一元二次方程.
不是整式方程
含两个未知数
化简整理 x2-3x+2=0
少了限制条件 a≠0
1.一元二次方程的概念
新知探究
想一想
一元一次方程与一元二次方程有什么区别与联系?
一元一次方程 一元二次方程
一般式
相同点
不同点
ax=b (a≠0)
ax2+bx+c=0 (a≠0)
整式方程,只含有一个未知数
未知数最高次数是1
未知数最高次数是2
新知探究
了解了一元二次方程的概念和一般形式,你会把一元二次方程化为一般形式吗?
下列方程是一元二次方程吗?若是,指出其中的二次项系数、一次项系数和常数项.
(1)3x (1 – x ) + 10 = 2( x + 2)
(2)5x ( x + 1) + 7 = 5x2 - 4.
解:(1)去括号, 得
3x - 3x2 + 10 = 2x + 4.
移项, 合并同类项, 得
- 3x2 + x + 6 = 0,
这是一元二次方程, 其中二次项系数是-3, 一次项系数是1, 常数项是6.
2.一元二次方程的一般形式
新知探究
(2) 5x ( x + 1) + 7 = 5x2 - 4.
去括号, 得
5x2 + 5x + 7 = 5x2 - 4.
移项, 合并同类项, 得
5x + 11 = 0,
可以看出这个方程没有二次项,因此这是一元一次方程, 不是一元二次方程.
2.一元二次方程的一般形式
新知探究
(1)在确定一元二次方程各项系数时,首先把一元二次方程转化成一般形式,如果在一般形式中二次项系数为负数,那么最好在方程左右两边同乘-1,使二次项系数变为正数;
(2)指出一元二次方程的各项系数时,一定要带上前面的符号;
(3)一元二次方程转化为一般形式后,若没有出现一次项,则=0;若没有出现常数项,则=0.
2.一元二次方程的一般形式
新知探究
如图,一块长方形地,长为200米,建筑商将它分为 A、B、C三个区域,A,B为正方形。现计划A区域建筑住宅区,B区域建筑商场,C区域开辟为公园。若已知C区域的面积为3200,设C区域的长为米,列出关于x的方程?
3.列一元二次方程
A
B
C
200米
x
解:由题意知A,B为正方形,
所以C区域的宽为200-x-x=200-2x
所以(200?2????)×????=3200
去括号移项整理得
03 典型例题
典型例题
1. 下列哪些是一元二次方程?
3x+2=5x-2
x2=0
(x+3)(2x-4)=x2
3y2=(3y+1)(y-2)
x2=x3+x2-1
3x2=5x-1
×
√
√
×
×
√
典型例题
2.一元二次方程 化为一般形式为:_________,二次项系数为___,一次项系数为___,常数项为_____.
=0
其中二次项系数是 1, 一次项系数是 -8, 常数项是 -4.
解析:
3.两个正方形,小正方形的边长比大正方形的边长的一半多4cm,大正方形的面积比小正方形的面积的2倍少32平方厘米,设大正方形边长为x,列出关于x的方程?
典型例题
解:根据题意,小正方形的边长为
大正方形的面积为
去括号移项整理得
04 拓展提高
拓展提高
百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元,为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存,经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件。
要想平均每天销售这种童装1200元,那么每件童装应降价多少元?
思路:审题→列方程→解未知数
解:设每件童装降价x元,那么根据题意每件盈利40-(元),可卖出20+2件
因此有方程式
解得
因为要尽量减少库存,所以取
答:每件童装应降价20元。
05 课堂小结
课堂小结
一元二次方程
概念
是整式方程;
含一个未知数;
最高次数是2.
一般形式
ax2+bx+c=0 (a ≠0)
其中(a≠0)是一元二次方程的必要条件;
列方程解应用问题
准确审题→列方程→解未知数
06 作业布置
完成课本习题2.1 A、B组
作业布置
谢 谢 观 看
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
