湘教版九年级数学上册第1章 反比例函数1.3 反比例函数的应用教学课件(共24张)
文档属性
| 名称 | 湘教版九年级数学上册第1章 反比例函数1.3 反比例函数的应用教学课件(共24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-16 23:39:05 | ||
图片预览








文档简介
(共24张PPT)
反比例函数的应用
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
寒假到了,小明正与几个同伴在结冰的河面上溜冰,突然发现前面有一处冰出现了裂痕,小明立即告诉同伴分散趴在冰面上,匍匐离开了危险区。
你能解释一下小明这样做的道理吗?
想学习更多吗?让我们一起开启用“反比例函数”解决实际问题的探险之旅吧!
02 新知探究
新知探究
1.反比例函数与简单的数学问题相结合
例:长方形的面积为8,它的长 a 与宽 b 的函数关系式是___________.
解析:由长方形面积公式得 8=ab
,又结合实际情况知 ????>0
故填(????>0)
(????>0)
*小总结:数学中一些常见问题可以利用反比例函数求解,
但构建模型时不要忽略反比例函数的基本性质。
新知探究
2.反比例函数在实际生活中的应用
1. 某公司计划新建一个容积V(m3)一定的长方形污水处理池,池的底面积S(m2)与其深度h(m)之间函数关系式为(),这个函数的图像大致是( )
C
新知探究
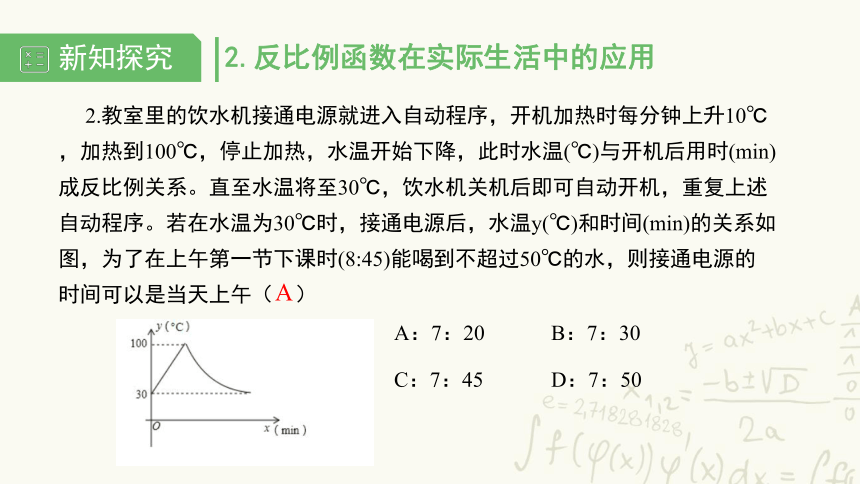
2.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系。直至水温将至30℃,饮水机关机后即可自动开机,重复上述自动程序。若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如 图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午( )
2.反比例函数在实际生活中的应用
A:7:20
B:7:30
C:7:45
D:7:50
A
新知探究
解析:先求出两个函数的解析式,再计算出一个循环周期需要的时间,求出水温不超过50℃的时间段
解:∵开机加热时每分钟上升10℃. ∴从30 ℃到100℃需要7分钟.
2.反比例函数在实际生活中的应用
设一次函数关系式为:, 根据题意知
∴ (),令
设反比例函数关系式为:,
将(7,100)代入得k=700,
∴ ,将y=30代入得;
新知探究
2.反比例函数在实际生活中的应用
∴,
令=50,解得
所以,饮水机的一个循环周期为分钟,每个循环周期内,在时间段内,水温不超过50℃
根据以上分析,分别进行判断可知选项A可行:
7:20到8:45之间有85分钟,85- X=15,位于时间段内,故可行
03 典型例题
典型例题
1. 矩形面积为 6,它的长 y 与宽 x 之间的函数关系用
图象可表示为 ( )
B.
A.
C.
D.
B
2. A、B两城市相距720千米,一列火车从A城去B城.
(1) 火车的速度 v (千米/时) 和行驶的时间 t (时)
之间的函数关系是________.
(2) 若到达目的地后,按原路匀速返回,并要求
在 3 小时内回到 A 城,则返回的速度不能低
于____________.
240千米/时
典型例题
3.某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1000m3 生活垃圾运走.
(1) 假如每天能运xm3,所需时间为y天,写出y与x之间的函数关系式。
提示:垃圾总量=每天运送量× 运送天数
典型例题
解:垃圾总量=每天运送量× 运送天数
所以 1000=x × y
故关系式为
典型例题
(2) 若每辆拖拉机一天能运10m3,则4辆这样的拖拉机要多少天才能运玩?
解:垃圾总量=每天运送量× 运送天数
所以4辆拖拉机每天运动量为10 ×4=40m3
需要的运送天数为
(3) 在(2)的情况下,运了10天后,剩下的任务要在不超过6天的时间完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
典型例题
解:运了10天后剩余垃圾量为1000-40×10=600m3
设需要增加辆拖拉机,按照题意剩余任务运送天数不超过6天,所以≤6
解得≥100,因此≥6
所以至少需要增加6辆这样的拖拉机才能按时完成任务
04 拓展提高
拓展提高
学校锅炉旁建有一个储煤库,开学时购进一批煤,现在知道:按每天用煤 0.6 吨计算,一学期 (按150天计算) 刚好用完. 若每天的耗煤量为 x 吨,那么这批煤能维持 y 天.
(1) 则 y 与 x 之间有怎样的函数关系?
解:煤的总量为:0.6×150=90 (吨),
根据题意有
(x>0).
拓展提高
(2) 若每天节约 0.1 吨,则这批煤能维持多少天?
解:∵ 每天节约 0.1 吨煤,
∴ 每天的用煤量为 0.6-0.1=0.5 (吨),
∴ 这批煤能维持 180 天.
05 课堂小结
课堂小结
反比例函数的应用
过程:
分析实际情境→建立函数模型→明确数学问题
注意:
实际问题中的两个变量往往都只能取非负值;
作实际问题中的函数图像时,横、纵坐标的单
位长度不一定相同
06 作业布置
1、完成课本习题1.3 A、B组
2、认真复习本章所学,理清实际问题中的函数关系,能够准确的将反比例关系表达式展现出来,完成复习题1
作业布置
谢 谢 观 看
反比例函数的应用
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
寒假到了,小明正与几个同伴在结冰的河面上溜冰,突然发现前面有一处冰出现了裂痕,小明立即告诉同伴分散趴在冰面上,匍匐离开了危险区。
你能解释一下小明这样做的道理吗?
想学习更多吗?让我们一起开启用“反比例函数”解决实际问题的探险之旅吧!
02 新知探究
新知探究
1.反比例函数与简单的数学问题相结合
例:长方形的面积为8,它的长 a 与宽 b 的函数关系式是___________.
解析:由长方形面积公式得 8=ab
,又结合实际情况知 ????>0
故填(????>0)
(????>0)
*小总结:数学中一些常见问题可以利用反比例函数求解,
但构建模型时不要忽略反比例函数的基本性质。
新知探究
2.反比例函数在实际生活中的应用
1. 某公司计划新建一个容积V(m3)一定的长方形污水处理池,池的底面积S(m2)与其深度h(m)之间函数关系式为(),这个函数的图像大致是( )
C
新知探究
2.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系。直至水温将至30℃,饮水机关机后即可自动开机,重复上述自动程序。若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如 图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午( )
2.反比例函数在实际生活中的应用
A:7:20
B:7:30
C:7:45
D:7:50
A
新知探究
解析:先求出两个函数的解析式,再计算出一个循环周期需要的时间,求出水温不超过50℃的时间段
解:∵开机加热时每分钟上升10℃. ∴从30 ℃到100℃需要7分钟.
2.反比例函数在实际生活中的应用
设一次函数关系式为:, 根据题意知
∴ (),令
设反比例函数关系式为:,
将(7,100)代入得k=700,
∴ ,将y=30代入得;
新知探究
2.反比例函数在实际生活中的应用
∴,
令=50,解得
所以,饮水机的一个循环周期为分钟,每个循环周期内,在时间段内,水温不超过50℃
根据以上分析,分别进行判断可知选项A可行:
7:20到8:45之间有85分钟,85- X=15,位于时间段内,故可行
03 典型例题
典型例题
1. 矩形面积为 6,它的长 y 与宽 x 之间的函数关系用
图象可表示为 ( )
B.
A.
C.
D.
B
2. A、B两城市相距720千米,一列火车从A城去B城.
(1) 火车的速度 v (千米/时) 和行驶的时间 t (时)
之间的函数关系是________.
(2) 若到达目的地后,按原路匀速返回,并要求
在 3 小时内回到 A 城,则返回的速度不能低
于____________.
240千米/时
典型例题
3.某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1000m3 生活垃圾运走.
(1) 假如每天能运xm3,所需时间为y天,写出y与x之间的函数关系式。
提示:垃圾总量=每天运送量× 运送天数
典型例题
解:垃圾总量=每天运送量× 运送天数
所以 1000=x × y
故关系式为
典型例题
(2) 若每辆拖拉机一天能运10m3,则4辆这样的拖拉机要多少天才能运玩?
解:垃圾总量=每天运送量× 运送天数
所以4辆拖拉机每天运动量为10 ×4=40m3
需要的运送天数为
(3) 在(2)的情况下,运了10天后,剩下的任务要在不超过6天的时间完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
典型例题
解:运了10天后剩余垃圾量为1000-40×10=600m3
设需要增加辆拖拉机,按照题意剩余任务运送天数不超过6天,所以≤6
解得≥100,因此≥6
所以至少需要增加6辆这样的拖拉机才能按时完成任务
04 拓展提高
拓展提高
学校锅炉旁建有一个储煤库,开学时购进一批煤,现在知道:按每天用煤 0.6 吨计算,一学期 (按150天计算) 刚好用完. 若每天的耗煤量为 x 吨,那么这批煤能维持 y 天.
(1) 则 y 与 x 之间有怎样的函数关系?
解:煤的总量为:0.6×150=90 (吨),
根据题意有
(x>0).
拓展提高
(2) 若每天节约 0.1 吨,则这批煤能维持多少天?
解:∵ 每天节约 0.1 吨煤,
∴ 每天的用煤量为 0.6-0.1=0.5 (吨),
∴ 这批煤能维持 180 天.
05 课堂小结
课堂小结
反比例函数的应用
过程:
分析实际情境→建立函数模型→明确数学问题
注意:
实际问题中的两个变量往往都只能取非负值;
作实际问题中的函数图像时,横、纵坐标的单
位长度不一定相同
06 作业布置
1、完成课本习题1.3 A、B组
2、认真复习本章所学,理清实际问题中的函数关系,能够准确的将反比例关系表达式展现出来,完成复习题1
作业布置
谢 谢 观 看
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
