湘教版九年级数学上册第1章 反比例函数1.2 反比例函数的图像和性质教学课件(共31张)
文档属性
| 名称 | 湘教版九年级数学上册第1章 反比例函数1.2 反比例函数的图像和性质教学课件(共31张) |  | |
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-17 07:16:51 | ||
图片预览







文档简介
(共31张PPT)
反比例函数的图形
和性质
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
我们已经学习了用“描点法”画一次函数的图像,并且知道一次函数的图象是一条直线,那么怎样画反比例函数 ( 为常数,)的图象呢?它的图象的形状是怎样的呢?
x
y
是这种用曲线组成的图象还是和一次函数一样是一条直线呢?
02 新知探究
新知探究
1.反比例函数的图象(k>0)
反比例函数的图像是什么样的呢?我们按照反比例系数的正负来区分讲解吧:
同学们能在直角坐标系中画出反比例函数 与 的图象吗?
提示:画函数的图象步骤一般分为:列表→描点→连线. 需要注意的是在反比例函数中自变量 .
新知探究
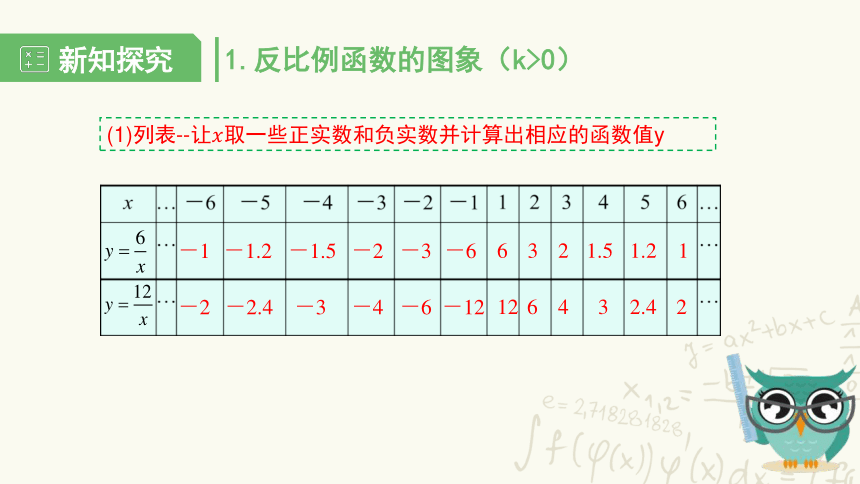
(1)列表--让取一些正实数和负实数并计算出相应的函数值y
-1
-2
-1.2
-2.4
-1.5
-3
-2
-4
-3
-6
-6
6
3
6
2
4
1.5
3
1.2
2.4
1
2
1.反比例函数的图象(k>0)
-12
12
-1
1
2
3
4
5
6
x
-2
-3
-4
-5
1
2
3
4
5
6
-1
-2
-3
-4
-5
新知探究
1.反比例函数的图象(k>0)
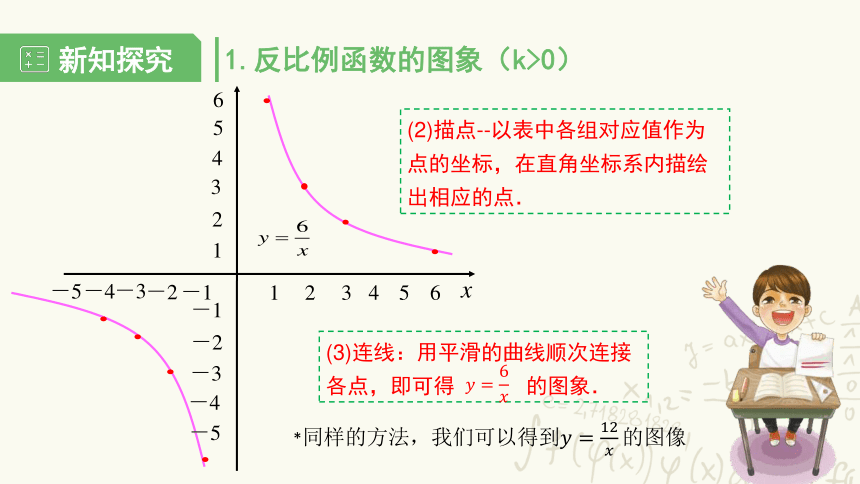
(2)描点--以表中各组对应值作为点的坐标,在直角坐标系内描绘出相应的点.
(3)连线:用平滑的曲线顺次连接各点,即可得 的图象.
*同样
新知探究
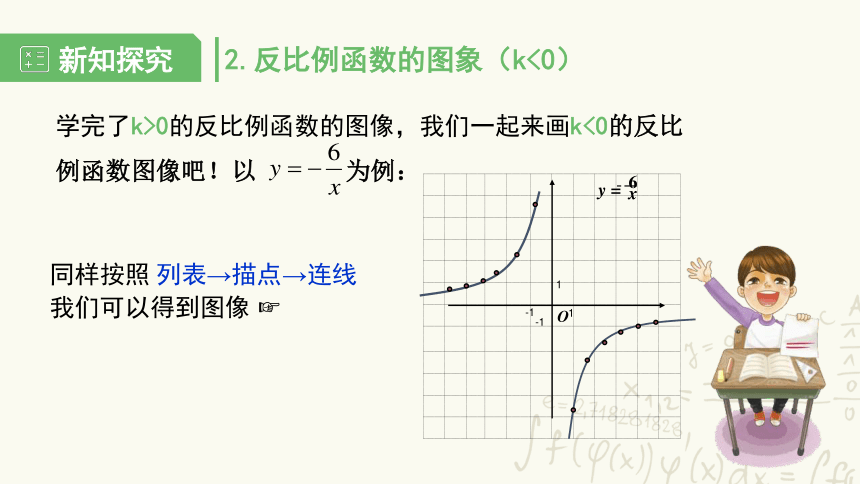
2.反比例函数的图象(k<0)
学完了k>0的反比例函数的图像,我们一起来画k<0的反比例函数图像吧!以 为例:
同样按照 列表→描点→连线
我们可以得到图像 ?
y =
x
6
O
-1
1
1
-1
新知探究
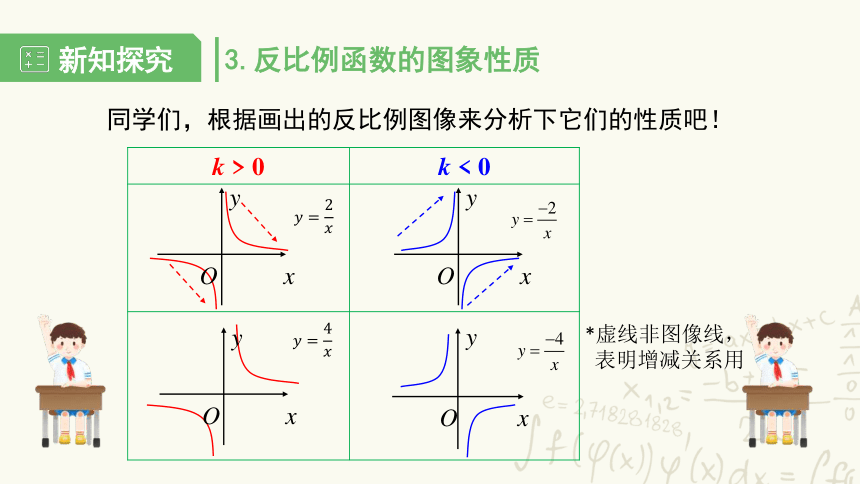
同学们,根据画出的反比例图像来分析下它们的性质吧!
3.反比例函数的图象性质
k > 0 k < 0
y
x
O
y
x
O
y
x
O
y
x
O
*虚线非图像线,
表明增减关系用
新知探究
根据上图你能总结出来反比例函数的图象性质吗?
3.反比例函数的图象性质
k k > 0 k < 0
共同 双曲线,即由两支曲线组成
象限 分别位于一、三象限 分别位于二、四象限
增减性 每个象限内,y 随x 的增大而减小 每个象限内,y 随x 的增大而增大
其他特点 1.轴对称图形,也是以原点为对称中心的中心对称图形
2.曲线的发展趋势靠近坐标轴,但不能和坐标轴相交
k 的正负决定反比例函数所在的象限和增减性哟
新知探究
A.
x
y
C.
x
y
o
x
y
o
D.
o
y
x
B.
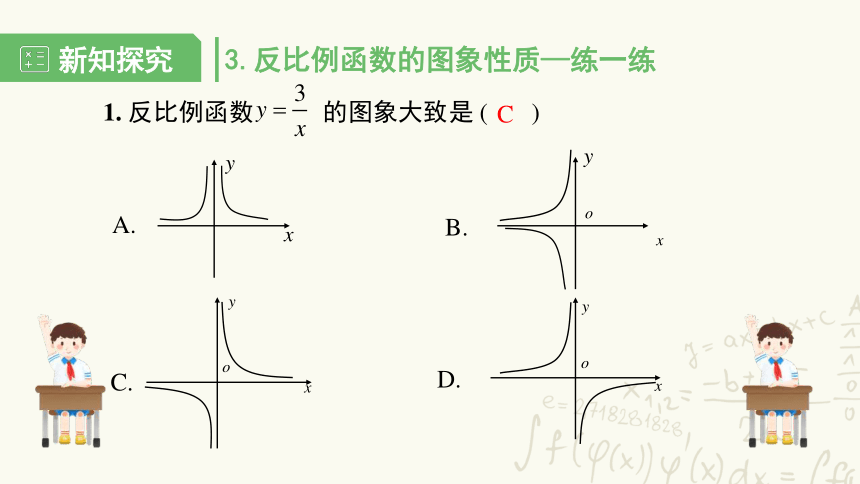
1. 反比例函数 的图象大致是 ( )
C
3.反比例函数的图象性质—练一练
新知探究
2. 点(2,y1)和(3,y2)在函数 上,则y1 y2
(填“>”“<”或“=”).
<
3.反比例函数的图象性质—练一练
3. 如图,已知直线y=mx与双曲线 的一个交点坐标为
(-1,3),则它们的另一个交点坐标是 ( )
A. (1,3) B. (3,1)
C. (1,-3) D. (-1,3)
C
解析:双曲线关于原点中心对称,因此两个交点坐标互为相反数
新知探究
y
x
o
A
C
如图所示,点A在反比例函数 的图象上,AC垂直x 轴于点C,且的面积是2,求该反比例函数的表达式。
解析:先设点A的坐标,然后用A的坐标表示的面积,进而求出k的值
3.反比例函数的图象性质—k的几何意义
新知探究
解:
3.反比例函数的图象性质—k的几何意义
新知探究
y
x
O
A
B
即:S△AOB = .
S□ABCO=|????|
对于反比例函数而言,过双曲线上任意一点与原点所连的线段、坐标轴与向坐标轴作垂线所围成的直角三角形的面积等于值的一半,同理如图围成的矩形面积等于值
3.反比例函数的图象性质—k的几何意义
小归纳
C
新知探究
练习:如图,过反比例函数 图象上的一点 P,作
PA⊥x 轴于A. 若△POA 的面积为 6,则 k = .
y
x
O
P
A
提示:当反比例函数图象在第二、四象限时,注意
k<0.
-12
3.反比例函数的图象性质—k的几何意义
03 典型例题
典型例题
1. 已知反比例函数 的图象过点(-2,-3),函
数图象上有两点 A( ,y1),B(5,y2),则 y1与y2
的大小关系为 ( )
A. y1 > y2
C. y1 < y2
B. y1 = y2
D. 无法确定
提示:可知反比例函数的解析式为 ,因为6>0,且 A,B 两点均位于第一象限部分,根据 >5,可知y1,y2的大小关系.
C
考点:k > 0 时,函数值 y 随 x 的增大而减小
2.已知反比例函数的图象经过点 A (2,6).
(1) 这个函数的图象位于哪些象限?y 随 x 的增大如
何变化?
解:因为点 A (2,6) 在第一象限,所以这个函数的
图象位于第一、三象限;
在每一个象限内,y 随 x 的增大而减小.
典型例题
考点:k > 0 时,反函数图像位于第一、三象限,函数值 y 随 x 的增大而减小
(2) 点B(3,4),C( , ),D(2,5)是否在这个
函数的图象上?
解:设这个反比例函数的解析式为 ,因为点
A (2,6)在其图象上,所以有 ,解得 k =12.
因为点 B,C 的坐标都满足该解析式,而点 D的坐标不满足,所以点 B,C 在这个函数的图象上,点 D 不在这个函数的图象上.
所以反比例函数的解析式为 .
典型例题
3. 下列关于反比例函数 的图象的三个结论:
(1) 经过点 (-1,12) 和点 (10,-1.2);
(2) 在每一个象限内,y 随 x 的增大而减小;
(3) 双曲线位于二、四象限.
其中正确的是 (填序号).
(1)(3)
典型例题
考点:k > 0 时,反函数图像位于第一、三象限,函数值 y 随 x 的增大而增大
4. 已知反比例函数 ,y 随 x 的增大而增大,求a的值.
解:因为函数为反比例函数,所以
a2+a-7=-1,
又由于y 随 x 的增大而增大可知a-1<0.
解得 a=-3.
典型例题
5.如图,点 A 是反比例函数 (x>0)的图象上
任意一点,AB//x 轴交反比例函数 (x<0) 的图象于点 B,以 AB 为边作平行四边形 ABCD,其中点 C,D 在 x 轴上,则 S平行四边形ABCD =___.
5
3
2
B
C
A
D
典型例题
解析: 根据反函数的几何意义,任一点与原点和坐标轴围成的矩形面积为|????|
因此S平行四边形ABCD =|2|+|-3|=5
04 拓展提高
拓展提高
点 (a-1,y1),(a+1,y2)在反比例函数 (k>0)
的图象上,若y1<y2,求a的取值范围.
解:由题意知,在图象的每一支上,y 随 x 的增大而减小.
① 当这两点在图象的同一支上时,
∵y1<y2,∴a-1>a+1, 无解;
②当这两点分别位于图象的两支上时,
∵y1<y2,∴必有 y1<0<y2.
∴a-1<0,a+1>0, 解得:-1<a<1.
故 a 的取值范围为:-1<a<1.
05 课堂小结
课堂小结
k k > 0 k < 0
共同 双曲线,即由两支曲线组成
象限 分别位于一、三象限 分别位于二、四象限
增减性 每个象限内,y 随x 的增大而减小 每个象限内,y 随x 的增大而增大
其他特点 1.轴对称图形,也是以原点为对称中心的中心对称图形
2.曲线的发展趋势靠近坐标轴,但不能和坐标轴相交
反比例函数的图象和性质
06 作业布置
完成课本习题1.2 A、B组
作业布置
谢 谢 观 看
反比例函数的图形
和性质
教学课件
湘教版九年级上册
01 新课导入
目录
03 典型例题
02 新知探究
04 拓展提高
05 课堂小结
06 作业布置
01 新课导入
新课导入
我们已经学习了用“描点法”画一次函数的图像,并且知道一次函数的图象是一条直线,那么怎样画反比例函数 ( 为常数,)的图象呢?它的图象的形状是怎样的呢?
x
y
是这种用曲线组成的图象还是和一次函数一样是一条直线呢?
02 新知探究
新知探究
1.反比例函数的图象(k>0)
反比例函数的图像是什么样的呢?我们按照反比例系数的正负来区分讲解吧:
同学们能在直角坐标系中画出反比例函数 与 的图象吗?
提示:画函数的图象步骤一般分为:列表→描点→连线. 需要注意的是在反比例函数中自变量 .
新知探究
(1)列表--让取一些正实数和负实数并计算出相应的函数值y
-1
-2
-1.2
-2.4
-1.5
-3
-2
-4
-3
-6
-6
6
3
6
2
4
1.5
3
1.2
2.4
1
2
1.反比例函数的图象(k>0)
-12
12
-1
1
2
3
4
5
6
x
-2
-3
-4
-5
1
2
3
4
5
6
-1
-2
-3
-4
-5
新知探究
1.反比例函数的图象(k>0)
(2)描点--以表中各组对应值作为点的坐标,在直角坐标系内描绘出相应的点.
(3)连线:用平滑的曲线顺次连接各点,即可得 的图象.
*同样
新知探究
2.反比例函数的图象(k<0)
学完了k>0的反比例函数的图像,我们一起来画k<0的反比例函数图像吧!以 为例:
同样按照 列表→描点→连线
我们可以得到图像 ?
y =
x
6
O
-1
1
1
-1
新知探究
同学们,根据画出的反比例图像来分析下它们的性质吧!
3.反比例函数的图象性质
k > 0 k < 0
y
x
O
y
x
O
y
x
O
y
x
O
*虚线非图像线,
表明增减关系用
新知探究
根据上图你能总结出来反比例函数的图象性质吗?
3.反比例函数的图象性质
k k > 0 k < 0
共同 双曲线,即由两支曲线组成
象限 分别位于一、三象限 分别位于二、四象限
增减性 每个象限内,y 随x 的增大而减小 每个象限内,y 随x 的增大而增大
其他特点 1.轴对称图形,也是以原点为对称中心的中心对称图形
2.曲线的发展趋势靠近坐标轴,但不能和坐标轴相交
k 的正负决定反比例函数所在的象限和增减性哟
新知探究
A.
x
y
C.
x
y
o
x
y
o
D.
o
y
x
B.
1. 反比例函数 的图象大致是 ( )
C
3.反比例函数的图象性质—练一练
新知探究
2. 点(2,y1)和(3,y2)在函数 上,则y1 y2
(填“>”“<”或“=”).
<
3.反比例函数的图象性质—练一练
3. 如图,已知直线y=mx与双曲线 的一个交点坐标为
(-1,3),则它们的另一个交点坐标是 ( )
A. (1,3) B. (3,1)
C. (1,-3) D. (-1,3)
C
解析:双曲线关于原点中心对称,因此两个交点坐标互为相反数
新知探究
y
x
o
A
C
如图所示,点A在反比例函数 的图象上,AC垂直x 轴于点C,且的面积是2,求该反比例函数的表达式。
解析:先设点A的坐标,然后用A的坐标表示的面积,进而求出k的值
3.反比例函数的图象性质—k的几何意义
新知探究
解:
3.反比例函数的图象性质—k的几何意义
新知探究
y
x
O
A
B
即:S△AOB = .
S□ABCO=|????|
对于反比例函数而言,过双曲线上任意一点与原点所连的线段、坐标轴与向坐标轴作垂线所围成的直角三角形的面积等于值的一半,同理如图围成的矩形面积等于值
3.反比例函数的图象性质—k的几何意义
小归纳
C
新知探究
练习:如图,过反比例函数 图象上的一点 P,作
PA⊥x 轴于A. 若△POA 的面积为 6,则 k = .
y
x
O
P
A
提示:当反比例函数图象在第二、四象限时,注意
k<0.
-12
3.反比例函数的图象性质—k的几何意义
03 典型例题
典型例题
1. 已知反比例函数 的图象过点(-2,-3),函
数图象上有两点 A( ,y1),B(5,y2),则 y1与y2
的大小关系为 ( )
A. y1 > y2
C. y1 < y2
B. y1 = y2
D. 无法确定
提示:可知反比例函数的解析式为 ,因为6>0,且 A,B 两点均位于第一象限部分,根据 >5,可知y1,y2的大小关系.
C
考点:k > 0 时,函数值 y 随 x 的增大而减小
2.已知反比例函数的图象经过点 A (2,6).
(1) 这个函数的图象位于哪些象限?y 随 x 的增大如
何变化?
解:因为点 A (2,6) 在第一象限,所以这个函数的
图象位于第一、三象限;
在每一个象限内,y 随 x 的增大而减小.
典型例题
考点:k > 0 时,反函数图像位于第一、三象限,函数值 y 随 x 的增大而减小
(2) 点B(3,4),C( , ),D(2,5)是否在这个
函数的图象上?
解:设这个反比例函数的解析式为 ,因为点
A (2,6)在其图象上,所以有 ,解得 k =12.
因为点 B,C 的坐标都满足该解析式,而点 D的坐标不满足,所以点 B,C 在这个函数的图象上,点 D 不在这个函数的图象上.
所以反比例函数的解析式为 .
典型例题
3. 下列关于反比例函数 的图象的三个结论:
(1) 经过点 (-1,12) 和点 (10,-1.2);
(2) 在每一个象限内,y 随 x 的增大而减小;
(3) 双曲线位于二、四象限.
其中正确的是 (填序号).
(1)(3)
典型例题
考点:k > 0 时,反函数图像位于第一、三象限,函数值 y 随 x 的增大而增大
4. 已知反比例函数 ,y 随 x 的增大而增大,求a的值.
解:因为函数为反比例函数,所以
a2+a-7=-1,
又由于y 随 x 的增大而增大可知a-1<0.
解得 a=-3.
典型例题
5.如图,点 A 是反比例函数 (x>0)的图象上
任意一点,AB//x 轴交反比例函数 (x<0) 的图象于点 B,以 AB 为边作平行四边形 ABCD,其中点 C,D 在 x 轴上,则 S平行四边形ABCD =___.
5
3
2
B
C
A
D
典型例题
解析: 根据反函数的几何意义,任一点与原点和坐标轴围成的矩形面积为|????|
因此S平行四边形ABCD =|2|+|-3|=5
04 拓展提高
拓展提高
点 (a-1,y1),(a+1,y2)在反比例函数 (k>0)
的图象上,若y1<y2,求a的取值范围.
解:由题意知,在图象的每一支上,y 随 x 的增大而减小.
① 当这两点在图象的同一支上时,
∵y1<y2,∴a-1>a+1, 无解;
②当这两点分别位于图象的两支上时,
∵y1<y2,∴必有 y1<0<y2.
∴a-1<0,a+1>0, 解得:-1<a<1.
故 a 的取值范围为:-1<a<1.
05 课堂小结
课堂小结
k k > 0 k < 0
共同 双曲线,即由两支曲线组成
象限 分别位于一、三象限 分别位于二、四象限
增减性 每个象限内,y 随x 的增大而减小 每个象限内,y 随x 的增大而增大
其他特点 1.轴对称图形,也是以原点为对称中心的中心对称图形
2.曲线的发展趋势靠近坐标轴,但不能和坐标轴相交
反比例函数的图象和性质
06 作业布置
完成课本习题1.2 A、B组
作业布置
谢 谢 观 看
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
